Conformal Quantile Regression for Probabilistic Constitutive Modeling of Anisotropic Soft Materials

Abstract: Biological soft tissues exhibit substantial inter-subject variability, making the automation of constitutive material modeling essential for patient-specific analysis and design. Such materials are not only highly nonlinear but also display intrinsic stochasticity arising from their complex and heterogeneous microstructure. Despite recent advances in data-driven constitutive modeling, most existing approaches remain deterministic and fail to quantify predictive uncertainty, thereby limiting their reliability in downstream mechanical analyses. In this work, we propose a probabilistic, data-driven constitutive modeling framework for anisotropic soft materials that explicitly accounts for uncertainty through conformalized quantile regression applied to tensor-valued fields. The proposed framework is built upon a strain-invariant, polyconvex formulation that ensures thermodynamic consistency and promotes robust predictive performance, including in extrapolative regimes. A key advantage of the proposed approach is its simplicity: it can be applied in a plug-and-play manner to endow existing deterministic models with probabilistic predictions, while remaining distribution-free and requiring no assumptions on the underlying data distribution. Moreover, the method is straightforward to train, scalable to models with a large number of parameters, and avoids Monte Carlo sampling at inference, making it computationally efficient and well suited for uncertainty propagation in large-scale mechanical simulations. The proposed method is validated using several benchmark datasets synthesized and collected from the literature.

• The paper introduces a probabilistic constitutive modeling framework using conformal quantile regression to quantify uncertainty in anisotropic soft materials.
• It integrates polyconvex strain-invariant representations with monotone neural networks to enforce thermodynamic and symmetry constraints, offering improved trainability and computational efficiency.
• Empirical evaluations on synthetic Mooney–Rivlin data, arterial wall models, and porcine valve experiments demonstrate robust extrapolation and calibrated uncertainty quantification.

Conformal Quantile Regression for Probabilistic Constitutive Modeling of Anisotropic Soft Materials

Introduction and Motivation

The work presents a probabilistic, data-driven constitutive modeling framework for anisotropic soft materials based on conformalized quantile regression (CQR) for tensor-valued fields. The motivation stems from the substantial inter-subject variability and intrinsic stochasticity in biological soft tissues, whose microstructural heterogeneity leads to highly nonlinear and sample-dependent constitutive responses. Despite advances in neural network-based constitutive modeling, most existing methods remain deterministic, neglecting the quantification of predictive uncertainties that are critical for patient-specific simulation and robust mechanics-based downstream analysis.

This framework is distinguished by three central methodological themes: (1) it enforces thermodynamic and symmetry constraints using polyconvex strain-invariant representations, (2) it leverages monotone neural architectures for improved robustness and learnability, and (3) it employs distribution-free conformalization as a tractable, scalable alternative to computationally expensive Bayesian inference. The overall goal is to provide calibrated, physically consistent uncertainty quantification for stress responses without any parametric assumption on data distribution or reliance on sampling at inference.

Physics-Constrained Parameterization: Polyconvexity and Anisotropy

The backbone of the model adapts the polyconvex anisotropic hyperelastic framework of Schröder et al., representing the strain energy as an additive sum of univariate functions of both classical and structural invariants. Anisotropy is parameterized through structural tensors encoding material symmetries; this allows the adaptation of the classical framework to directly infer fiber orientation effects from data.

All constitutive functions are required to be convex and non-decreasing, ensuring polyconvexity, which provides existence and stability guarantees for the variational problem and encodes necessary thermodynamic admissibility. Derivatives of these functions with respect to strain invariants are the quantities actually entering the stress computation; monotonicity of these derivative fields is both physically meaningful and numerically useful.

Monotone Neural Network Parameterization for Robust Learning

The work analyzes alternative parameterization strategies: direct input-convex neural networks (ICNNs) for strain energy functions versus monotone neural networks for gradient fields. The latter (monotone) approach provides improved trainability and computational efficiency, especially in univariate, possibly non-smooth scenarios, because monotonicity is more tractable to enforce than global convexity in function approximation. This leads to:

Figure 1: Synthetic example illustrating a smooth convex function (left) and its corresponding monotone derivative (right), used to compare performances of convex-function and gradient-based monotone parameterizations.

Direct parameterization of $\tilde{g}_k$ using monotone networks enables faster, more accurate regression of gradient (stress) responses from data, avoiding the instabilities typically observed with convex function parameterization.

Figure 2: Predicted gradients obtained using convex energy parameterization (left) and gradient-based monotone parameterization (right). The monotone approach more accurately captures the underlying stepwise gradient structure in this example.

Probabilistic Formulation: Quantile Regression and Conformalization

To enable uncertainty quantification, the model extends the deterministic backbone using tensorial quantile regression. Stress responses become tensor-valued random variables, and the model directly learns conditional quantile surfaces for all components using monotone neural networks, trained with the pinball loss and equipped with a non-crossing penalty to enforce the logical consistency of intervals. This eliminates the need for full Bayesian posterior inference and grants computational tractability for models with high parameter counts.

To restore finite-sample, distribution-free coverage in the presence of model misspecification or limited data, the authors formulate a tensor-valued extension of conformalized quantile regression. Componentwise nonconformity scores are computed on a calibration set, yielding conservative, coverage-guaranteed intervals for each stress component through the union bound.

Figure 3: Conformal adjustments computed using two calibration strategies: (a) trajectory-wise calibration and (b) pooled calibration across all trajectories. The horizontal axis denotes the number of calibration trajectories randomly selected from a batch of 256 trajectories. For each setting, the statistics of the conformal adjustments are computed over 10 independent random subsamples drawn from the calibration batch.

Trajectory-wise calibration, as shown, achieves more realistic uncertainty quantification by respecting experimental loading protocols and trajectory-level correlations.

Empirical Evaluation

Synthetic Mooney–Rivlin Data

In an isotropic regression scenario, the framework is benchmarked using Mooney–Rivlin synthetic data with input-parameter stochasticity. The results show that the model captures increasing heteroscedasticity under nonlinear loading and quantile intervals calibrated using CQR accurately cover the empirical distribution of stress responses.

Figure 4: Synthetic datasets generated using the Mooney–Rivlin constitutive model. (top) Twenty sets of material parameters are randomly sampled. (bottom) Mean and standard deviation computed over 500 parameter realizations.

Pinball loss training demonstrates convergence across all loading conditions.

Figure 5: Pinball loss for each loading case during training.

The fitted intervals before and after conformal adjustment are contrasted, again highlighting the ability of CQR to correct for finite-sample undercoverage.

Figure 6: (top) Quantile regression uncertainty intervals. (bottom) Conformalized quantile regression. Dashed lines denote the quantile predictions, while solid lines indicate the conformal-adjusted intervals.

Anisotropic Material: Synthetic Arterial Wall Data

The framework is tested on out-of-distribution (extrapolatory) stress–strain prediction for synthetic arterial wall data generated from parameterized models of Holzapfel et al. The learned model matches the mean and scatter of the reference, correlating accurately with true responses and providing reasonable extrapolation for previously unseen strain regimes; interval collapse in high-strain regimes signals the marginal nature of conformal coverage.

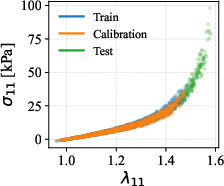
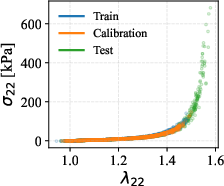
Figure 7: Training, calibration, and test data. (left) Stress–strain responses for uniaxial tests along different directions. (right) Mean and standard deviation of the data as a function of applied strain.

Figure 8: Pinball loss training history for the arterial wall data.

Figure 9: Model predictions on the test data (black dots) and uncertainty estimates given by the quantile predictions (dashed orange) and their conformal adjustments (solid purple). Blue points indicate the response corresponding to the mean material parameters of the reference model. The vertical red dashed line denotes the maximum strain used in training.

Experimental Data: Porcine Valve Leaflets Under Biaxial Loading

On real experimental data, the framework is successfully extended to anisotropic, multi-axis, and out-of-distribution settings, where it infers stress–strain uncertainty for porcine atrioventricular valve leaflets. It generalizes well to novel test loading protocols not included in training, indicating the efficacy of physics-encoded parameterization under realistic experimental variability.

Figure 10: Experimental data of porcine atrioventricular valve leaflets obtained under biaxial loading with varying loading ratios. The test data are shown in red.

Implications and Future Directions

This research establishes a practical, scalable path for probabilistic constitutive modeling in soft matter mechanics, sidestepping the computational bottlenecks of Bayesian inference and addressing the challenges of limited and non-i.i.d. experimental datasets. The method's plug-and-play design, distribution-free coverage without data distribution assumptions, robustness in extrapolation, and enforcement of thermodynamic constraints directly at the quantile level mark significant advantages over Gaussian process and Bayesian neural approaches.

Practically, this enables uncertainty propagation in large-scale mechanics simulations (e.g., patient-specific finite element analyses) without excessive computational load. Theoretically, it opens the door for future work incorporating epistemic uncertainty control—in particular, integrating recent developments in uncertainty-aware conformal quantile regression [Rossellini et al., 2024]—and for generalization to higher-order symmetry classes, e.g., by extending the representation beyond second-order to higher-order structural tensors.

Conclusion

The conformal quantile regression framework for anisotropic soft material modeling combines physics-based inductive bias with modern frequentist uncertainty quantification. The proposed method demonstrates strong coverage performance in both synthetic and experimental regimes, robust extrapolative generalization, and computational efficiency, while maintaining thermodynamic admissibility. Limitations include marginal coverage guarantees (primarily over aleatoric sources) and restricted expressivity for certain advanced material symmetries. Extensions to higher-order tensor parameterizations, as well as the incorporation of epistemic uncertainty quantification, present clear avenues for future development in the physics-informed probabilistic modeling of soft tissues and advanced materials.