Generalising E-prop to Deep Networks

Abstract: Recurrent networks are typically trained with backpropagation through time (BPTT). However, BPTT requires storing the history of all states in the network and then replaying them sequentially backwards in time. This computation appears extremely implausible for the brain to implement. Real Time Recurrent Learning (RTRL) proposes an mathematically equivalent alternative where gradient information is propagated forwards in time locally alongside the regular forward pass, however it has significantly greater computational complexity than BPTT which renders it impractical for large networks. E-prop proposes an approximation of RTRL which reduces its complexity to the level of BPTT while maintaining a purely online forward update which can be implemented by an eligibility trace at each synapse. However, works on RTRL and E-prop ubiquitously investigate learning in a single layer with recurrent dynamics. However, learning in the brain spans multiple layers and consists of both hierarchal dynamics in depth as well as time. In this mathematical note, we extend the E-prop framework to handle arbitrarily deep networks, deriving a novel recursion relationship across depth which extends the eligibility traces of E-prop to deeper layers. Our results thus demonstrate an online learning algorithm can perform accurate credit assignment across both time and depth simultaneously, allowing the training of deep recurrent networks without backpropagation through time.

• The paper extends E-prop with recursive eligibility updates that enable online learning in deep recurrent networks, approximating RTRL with tractable complexity.
• It demonstrates that nested recursions across time and depth allow efficient credit assignment without exponential computational cost.
• The study highlights practical challenges such as scaling eligibility traces for multilayer architectures and the need for empirical validation on complex tasks.

Generalising E-prop to Deep Networks: Derivation and Implications

Introduction

The training of recurrent neural networks (RNNs) has traditionally relied on Backpropagation Through Time (BPTT), but BPTT's memory requirements and lack of biological plausibility prompt interest in alternative methods. Real-Time Recurrent Learning (RTRL) provides an online gradient computation framework, but its prohibitive computational complexity has limited practical deployment. E-prop achieves a significant advance by approximating RTRL with local, online updates and tractable complexity. However, E-prop is typically formulated for single-layer recurrency. This work provides the first formal extension of the E-prop framework to arbitrarily deep recurrent neural networks, deriving a set of recursive eligibility trace updates spanning both depth and time. The analysis extends further to arbitrary directed acyclic graph (DAG) architectures with internal recurrency, suggesting broad applicability. Theoretical advantages and open challenges for scalable, biologically plausible learning in deep recurrent architectures are discussed.

Background: BPTT, RTRL, and E-prop

BPTT requires explicit unrolling of the network's computation through time, with gradient computation performed by backpropagating from the final loss through the sequence. This sequential backward phase is computationally efficient for modern digital hardware but requires storage of all intermediate states and activations (quadratic in sequence length and hidden dimension), creating substantial bottlenecks for long sequences as well as significant biological implausibility.

Figure 1: Schematic computation graph of a single-layer RNN model in the RTRL context, with BPTT gradients denoted in red.

RTRL, in contrast, computes gradients as the forward pass proceeds in time. It maintains a "sensitivity" tensor tracking how every parameter affects every hidden state as the system evolves. This enables truly online gradient calculation. However, in an $H$-dimensional hidden state, the required sensitivity tensor is $H \times H \times H$, and recurrent updates involve quartic ($O(H^4)$) computation. This cost is usually infeasible, except for very small networks or extremely long unrolled sequences.

E-prop circumvents these obstacles by approximating the full parameter-to-state sensitivity, replacing total derivatives with partial derivatives ($$\frac{dh}{d\theta} \approx \frac{\partial h}{\partial \theta}$$). This approach ignores indirect parameter-states couplings that cross via internal recurrent dynamics, collapsing the size of the eligibility traces to a tractable form (quadratic, matching BPTT) and reducing memory requirements to be constant in the sequence length.

Despite this progress, E-prop's standard formulation is limited to single recurrent layers, and the extension to deeper networks or hierarchically organized recurrent systems has not been developed. In practice and in biology, however, learning architectures are often deep and highly hierarchical.

Recursive Eligibility Updates for Deep Recurrent Networks

The central technical result is the derivation of nested recursive eligibility trace updates that propagate credit assignment both temporally (as in classic E-prop) and hierarchically in depth. Consider an $L$-layer, $T$-step system where each layer consists of recurrent units.

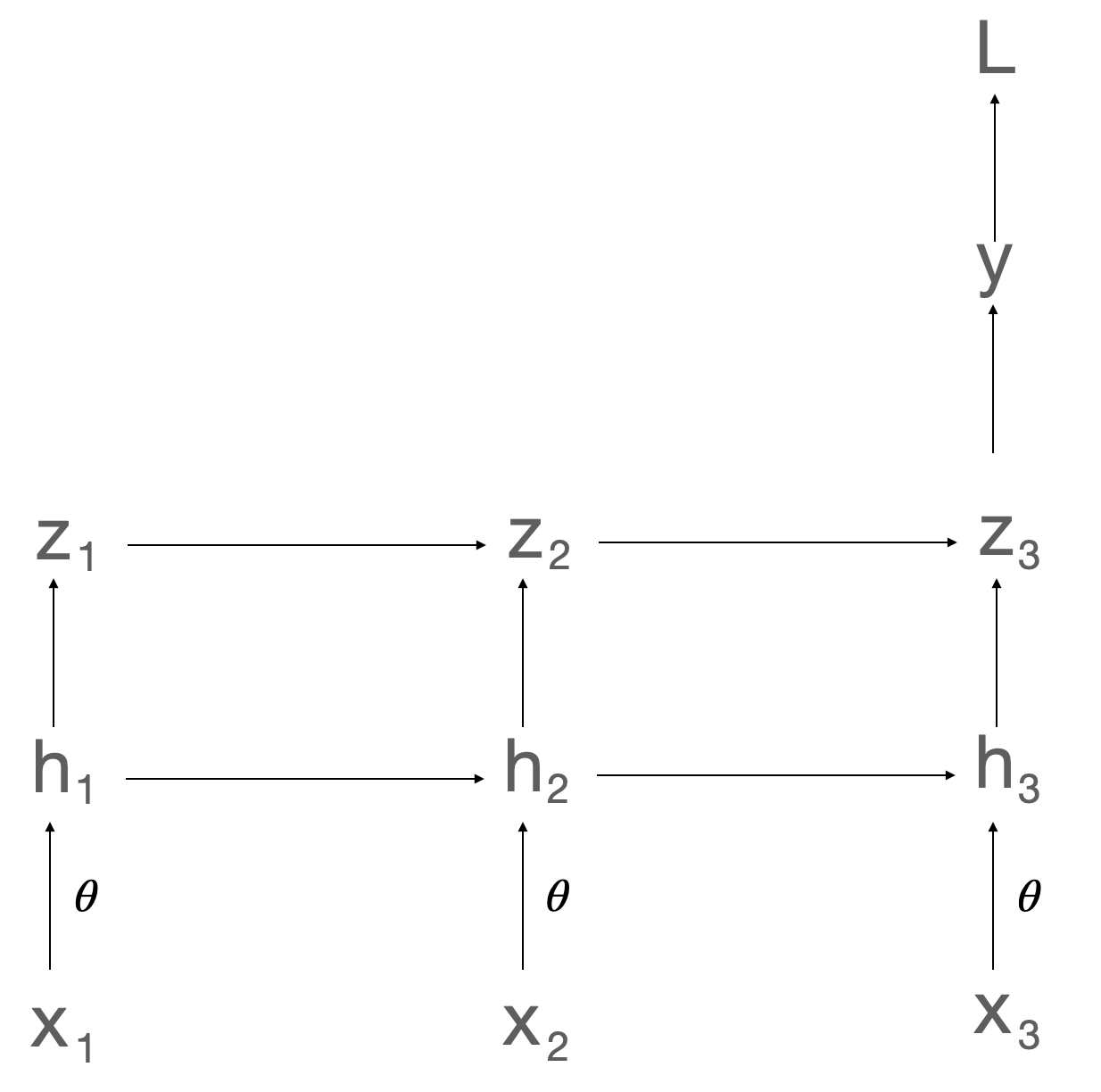
Figure 2: Schematic of a two-layer, three-timestep RNN used to derive the deep E-prop recursion.

For a two-layer, three-step RNN, the authors show that the gradient of the loss with respect to parameters involves two coupled recursions:

• A time-wise recursion in each layer, analogous to conventional E-prop.
• A depth-wise recursion, where the "eligibility trace" at a higher layer is a function of the trace at the lower layer, weighted by the inter-layer Jacobians.

Formally, for a set of hidden states $h_l^t$ at layer $l$ and timestep $t$, and parameters $\theta$, the eligibility trace for layer $l$ at timestep $t$, $\epsilon_t^l$, is computed as:

$$\epsilon_t^l = \frac{\partial h_t^l}{\partial h_{t-1}^l} \epsilon_{t-1}^l + \begin{cases} \frac{\partial h_t^l}{\partial h_t^{l-1}} \epsilon_t^{l-1}, & \text{if}\ l > 1 \ \frac{\partial h_t^l}{\partial \theta}, & \text{if}\ l = 1 \end{cases}$$

This unifies the temporal and hierarchical recurrences, and crucially, does not explode computational complexity: due to the dynamic programming structure of the recursion, linear complexity in depth (and not exponential) is retained despite the multiplicity of gradient paths in the unrolled network computation graph.

The derivation naturally extends to arbitrary DAG architectures featuring internal recurrency at each node, requiring only the summing of traces from all child nodes and the timewise trace.

Theoretical and Practical Implications

This formalism demonstrates the feasibility of structured, online, local learning rules in deep, hierarchical, and recurrent systems, thereby directly addressing long-standing open questions in the theory of biologically plausible learning. Contrary to earlier pessimism regarding deep RTRL-style recursions [Irie et al.], the analysis shows that the E-prop approximation's locality allows efficient summing over arbitrarily complex sets of gradient paths without incurring exponential cost.

The proposed algorithm serves as a unifying mathematical framework, extending both E-prop and (by using full derivatives) RTRL to deep networks and arbitrary DAGs. As such, the theory supplies a pathway for neural systems—including biological brains and scalable neuromorphic computing substrates—to perform correct credit assignment both in time and across multiple layers, without global replay or backward passes.

Nevertheless, several open concerns are highlighted:

• The absence of empirical validation leaves practical learning performance on challenging tasks unresolved.
• The approach requires distinct sets of eligibility traces for each parameter group in multilayer settings—a scaling challenge for deep architectures.
• The method accumulates gradients online but needs loss information from the "top" (last layer, last timestep), thus not supporting strictly synapse-local updates in the most constrained sense.
• The method relies on differentiability and access to requisite Jacobians, which may not be directly implementable in all biological or neuromorphic scenarios.
• Weight symmetry assumptions, as in standard backpropagation for MLPs, persist.

Future Directions

Theorizing aside, crucial practical questions remain:

• How closely does the E-prop approximation track BPTT in deep or complex RNNs, especially on long-horizon or compositional tasks?
• Can eligibility traces and local-only learning mechanisms be combined with higher-level mechanisms (neuromodulation, global error signals) in hierarchical recurrent systems for enhanced credit assignment?
• To what extent is the dynamic-programming recursion implementable in biologically realistic networks, possibly with further approximations, and can similar frameworks be realized in neuromorphic devices?
• Does the framework generalize to transformer-style or attention-based architectures with recurrence components?
• How can the memory and compute burden of multiple eligibility traces be reduced for very deep networks?

Conclusion

This work rigorously extends the E-prop local, online learning algorithm from single-layer RNNs to deep recurrent and hierarchically structured systems, maintaining computational tractability by leveraging recursive eligibility traces across both time and depth. While the theory closes a key gap in biologically motivated learning frameworks and highlights efficient dynamic-programming interpretations of gradient credit assignment, empirical assessment and further optimization remain essential for fully realizing scalable and practical deep recurrent learning algorithms.