High Dimensional Data Decomposition for Anomaly Detection of Textured Images

Abstract: In the realm of diverse high-dimensional data, images play a significant role across various processes of manufacturing systems where efficient image anomaly detection has emerged as a core technology of utmost importance. However, when applied to textured defect images, conventional anomaly detection methods have limitations including non-negligible misidentification, low robustness, and excessive reliance on large-scale and structured datasets. This paper proposes a texture basis integrated smooth decomposition (TBSD) approach, which is targeted at efficient anomaly detection in textured images with smooth backgrounds and sparse anomalies. Mathematical formulation of quasi-periodicity and its theoretical properties are investigated for image texture estimation. TBSD method consists of two principal processes: the first process learns the texture basis functions to effectively extract quasi-periodic texture patterns; the subsequent anomaly detection process utilizes that texture basis as prior knowledge to prevent texture misidentification and capture potential anomalies with high accuracy.The proposed method surpasses benchmarks with less misidentification, smaller training dataset requirement, and superior anomaly detection performance on both simulation and real-world datasets.

• The paper introduces TBSD, a framework that integrates learned quasi-periodic texture bases for precise anomaly detection in textured images.
• The paper employs rotational sampling and density clustering to capture texture directionality and distinguish anomalies from regular patterns.
• The paper demonstrates TBSD's superior performance with higher true positive rates and lower false positive rates compared to conventional methods in industrial applications.

High Dimensional Data Decomposition for Anomaly Detection of Textured Images

Introduction and Problem Formulation

The paper "High Dimensional Data Decomposition for Anomaly Detection of Textured Images" (2512.20432) addresses the significant limitations of existing anomaly detection methodologies for textured images, which are pervasive in industrial settings such as wood and steel inspection, surface NDT, and additive manufacturing. Conventional approaches—including RPCA, SSD, and FFT—exhibit suboptimal performance in the presence of mixed or quasi-periodic textures, frequent environmental disturbances, and absence of large labeled datasets, resulting in over-detection and reduced robustness.

To address these constraints, the authors propose the Texture Basis Integrated Smooth Decomposition (TBSD) framework. TBSD is designed to explicitly model image textures via learned quasi-periodic basis functions, thereby improving the discrimination between regular quasi-repetitive patterns and true sparse anomalies. Unlike previous approaches, TBSD incorporates mathematical modeling of quasi-periodicity and integrates this prior knowledge into the decomposition process.

Figure 1: Real-world textured images in manufacturing: wood, steel, and 3D-printed surfaces.

Theoretical Analysis: Quasi-periodicity

A major technical contribution is the rigorous formalization of quasi-periodicity in textured images. Instead of assuming strict periodicity, the paper introduces definitions and theorems for 1D and 2D quasi-periodicity, capturing texture modes that are "similar but not identical" across patches. The authors show that a textured image $Y$ can be decomposed as:

$Y = C_{bg} + C_{tex} + C_a + e$

where $C_{bg}$ is a low-rank smooth background, $C_{tex}$ the high-rank quasi-periodic texture, $C_a$ sparse anomalies, and $e$ noise.

Through dimension reduction along appropriate directions, extraction and representation of the quasi-periodic texture bases are mathematically grounded. The work extends notions of periodic and quasi-periodic signal composition, with constraints rigorously formulated, allowing systematic learning of texture modes.

Texture Basis Integrated Smooth Decomposition (TBSD) Methodology

The TBSD framework is composed of two major modules:

1. Texture Basis Function Learning (TBFL):

From a small set of defect-free images, TBSD extracts the smooth background by low-rank approximation and then learns a dictionary of quasi-periodic texture basis functions via rotationally-sampled 1D projections and density-based clustering. The sampling process efficiently identifies texture directionality, leveraging measures such as the difference in standard deviations of projections in the expansion and orthogonal directions.

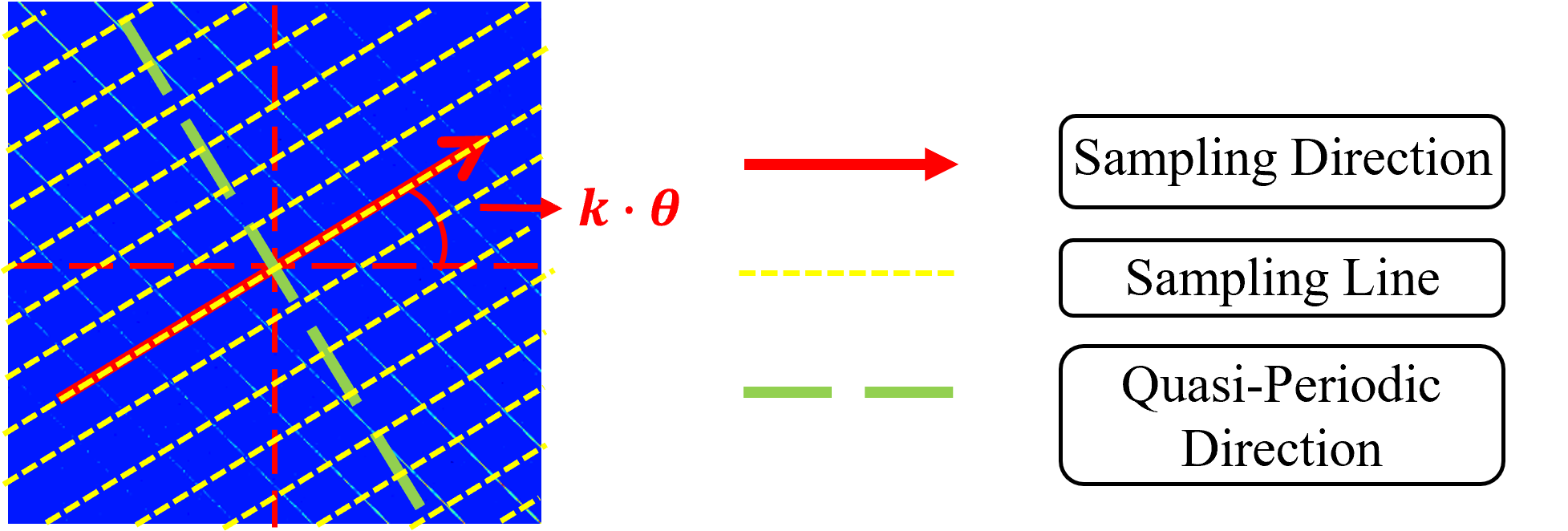
Figure 2: Schematic diagram of LSERA algorithm (rotation-based sampling for texture basis learning).

2. Anomaly Detection using Texture Priors:

Given a new image, TBSD decomposes it using both the pre-constructed smooth background basis and the learned texture dictionary. Anomalies are estimated as the residual after subtracting the reconstructed background and texture components, thus minimizing misclassification of regular texture patterns as anomalies.

Mathematically, the core optimization combines data fidelity, smoothness penalties, and sparsity constraints for both the background and texture dictionary coefficients.

Evaluation on Simulation and Real-World Datasets

Simulation Study:

Synthetic images with controlled texture and anomaly patterns are used to comparatively evaluate TBSD, RPCA, SSD, and FFT.

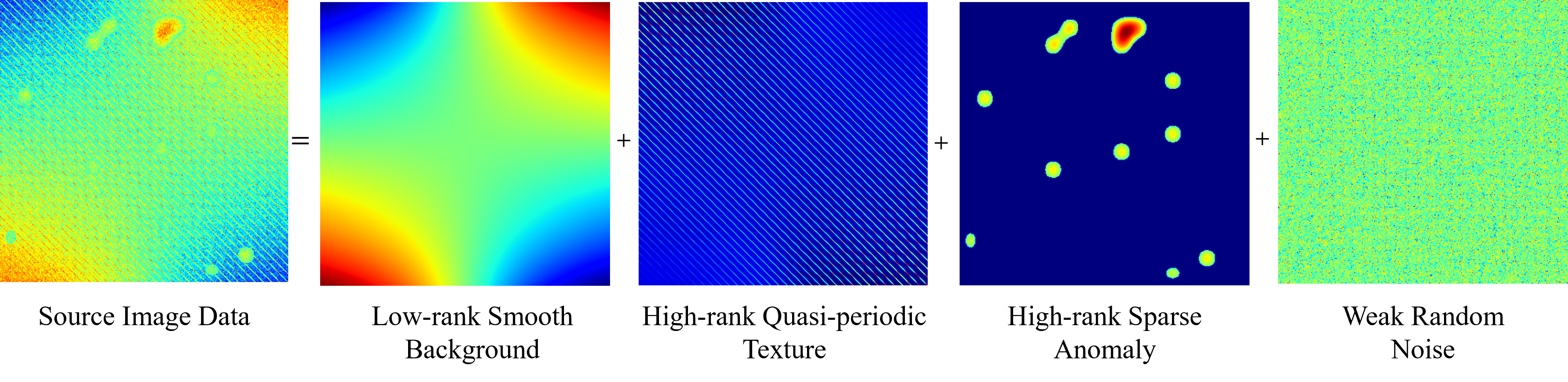
Figure 3: Simulation image showing decomposed components: background, textures, and anomalies.

Figure 4: Anomaly detection results; TBSD accurately isolates anomalies with minimal misclassification of textures.

Quantitatively, TBSD attains a mean True Positive Rate (TPR) of 0.43 and False Positive Rate (FPR) of 0.09 in various scenarios—substantially outperforming all baselines, particularly in cases of quasi-periodic and crossing-textures.

Real-World Case Study:

TBSD is validated on the MVTec AD wood dataset, where patches from defect-labeled samples are processed.

Figure 5: Comparative performance of anomaly detection methods on a wood surface patch.

TBSD achieves high anomaly recall with misidentification rates (FPR) consistently below 0.025, substantially lower than RPCA, SSD, and FFT. Visualization further confirms minimal confusion between texture and anomaly.

Figure 6: Visualization of accurate anomaly detection and suppressed false positives by TBSD in wood surface data.

Comprehensive statistics (including TPR, FPR, and per-patch detection ratio) demonstrate both accuracy and robustness to parameter variation.

Figure 7: Positive proportions of detected anomalies by patch across multiple test images.

Analysis and Implications

Model Generality and Limitations

TBSD successfully extends data decomposition-based anomaly detection to textured settings by:

• Formulating quasi-periodicity as a mathematical relaxation of periodicity, increasing modeling fidelity for industrial textures.
• Integrating unsupervised basis learning, reducing the need for defect annotations and large-scale normal data.
• Algorithmically balancing the contributions of background, texture, and sparse anomaly components to reduce over-detection.
• Demonstrating robustness to sub-optimal parameterization—however, the method's detection performance can still benefit from optimal tuning per image or patch.

Despite the focus on smooth backgrounds with sparse anomalies, the architecture is extensible to more complex scenes with adjustments to the basis set or with integration of supervised modules. Computational complexity is cubic in image size (comparable to RPCA/SSD); however, the empirical evaluation shows the overhead is justified by the gain in detection performance.

Figure 8: TBSD shows capability to detect both targeted and previously unseen anomaly types, beyond prior anomaly examples.

Future Directions

The mathematical insights open avenues for research in:

• Adaptive selection of basis functions for diverse types of textures in industrial images.
• Hybridization of TBSD with deep feature learning, possibly using pre-trained vision transformers as an additional basis.
• Incorporation of active or semi-supervised learning for rare or evolving anomaly classes.
• Real-time TBSD variants adapted for streaming or large-scale inspection.

Conclusion

The Texture Basis Integrated Smooth Decomposition (TBSD) approach delivers a principled, practical, and extensible solution to anomaly detection in textured images. By introducing and elucidating quasi-periodicity as a core modeling tool, TBSD overcomes the long-standing challenge of texture-anomaly confusion present in prior approaches. Its ability to perform with reduced data requirements, minimal annotation, and demonstrated robustness marks it as a significant advance for vision-driven manufacturing inspection and similar domains. Further refinement in parameter adaptation and hybrid integration with emerging deep features promises even broader applicability in the future.