MixKVQ: Query-Aware Mixed-Precision KV Cache Quantization for Long-Context Reasoning

Abstract: Long Chain-of-Thought (CoT) reasoning has significantly advanced the capabilities of LLMs, but this progress is accompanied by substantial memory and latency overhead from the extensive Key-Value (KV) cache. Although KV cache quantization is a promising compression technique, existing low-bit quantization methods often exhibit severe performance degradation on complex reasoning tasks. Fixed-precision quantization struggles to handle outlier channels in the key cache, while current mixed-precision strategies fail to accurately identify components requiring high-precision representation. We find that an effective low-bit KV cache quantization strategy must consider two factors: a key channel's intrinsic quantization difficulty and its relevance to the query. Based on this insight, we propose MixKVQ, a novel plug-and-play method that introduces a lightweight, query-aware algorithm to identify and preserve critical key channels that need higher precision, while applying per-token quantization for value cache. Experiments on complex reasoning datasets demonstrate that our approach significantly outperforms existing low-bit methods, achieving performance comparable to a full-precision baseline at a substantially reduced memory footprint.

• The paper introduces MixKVQ, a query-aware mixed-precision method that dynamically assigns bit-widths based on a composite channel salience metric.
• It achieves near-lossless performance at average bit-widths of 2.3–2.7 bits, outperforming prior 2-bit methods on complex chain-of-thought reasoning tasks.
• The method enables up to 2.25× larger batch sizes and 2.81× higher throughput, making long-context LLM inference more resource-efficient.

MixKVQ: Query-Aware Mixed-Precision KV Cache Quantization for Long-Context Reasoning

Motivation and Limitations of Existing KV Cache Quantization

LLMs designed for long Chain-of-Thought (CoT) reasoning present formidable resource requirements due to the linear scaling of Key-Value (KV) cache memory with context length. The resulting bottleneck is especially acute for models such as Qwen2.5 with large batch and context configurations, where the KV cache memory footprint can far exceed that of model weights. Recent proposals center on KV cache quantization—storing cache in lower bit-width representations—to address this. While 4-bit methods (e.g., KIVI) retain reasonable performance, extreme low-bit quantization (2-bit) consistently induces catastrophic degradation on complex reasoning tasks. This failure is most severe for fixed-precision schemes; by enforcing a uniform bit-width for all channels, these methods inadequately handle outlier channels with high dynamic ranges, precipitating significant quantization error and attention computation collapse.

Figure 1: Complex reasoning performance of different 2-bit KV cache quantization. Reasoning score is the average accuracy of AIME 2024-2025, MATH 500, GPQA, and LiveCodeBench.

Existing mixed-precision approaches attempt to mitigate this by assigning higher bit-widths to harder-to-quantize channels, typically judged via quantization error. However, this solely error-centric allocation still fails on complex CoT reasoning: channels with low errors can disproportionately affect attention fidelity if they are strongly attended by queries, and vice versa.

Detailed Error Analysis and the Need for Query Awareness

An in-depth investigation demonstrates two intertwined axes of quantization error accumulation: across model depth and token sequence. Within each key or value channel of the cache, absolute quantization errors can be highly non-uniform. Channel-wise visualization highlights that the key cache contains a small subset of extreme outlier channels, which dominate the quantization error profile, whereas value cache errors are comparatively uniform and amenable to aggressive quantization.

Figure 2: Absolute quantization error of key and value cache for Qwen-2.5-14B-Instruct model.

Critically, conventional error-based strategies neglect that the true impact of a channel is given not only by its own scale but by its interaction with the corresponding query magnitude. Empirically, there is a very weak correlation (Pearson's $r=0.16$) between key channel scale and average query magnitude over evaluation sequences. This observation invalidates the direct use of channel scale as a proxy for importance in quantization, as done by most prior work.

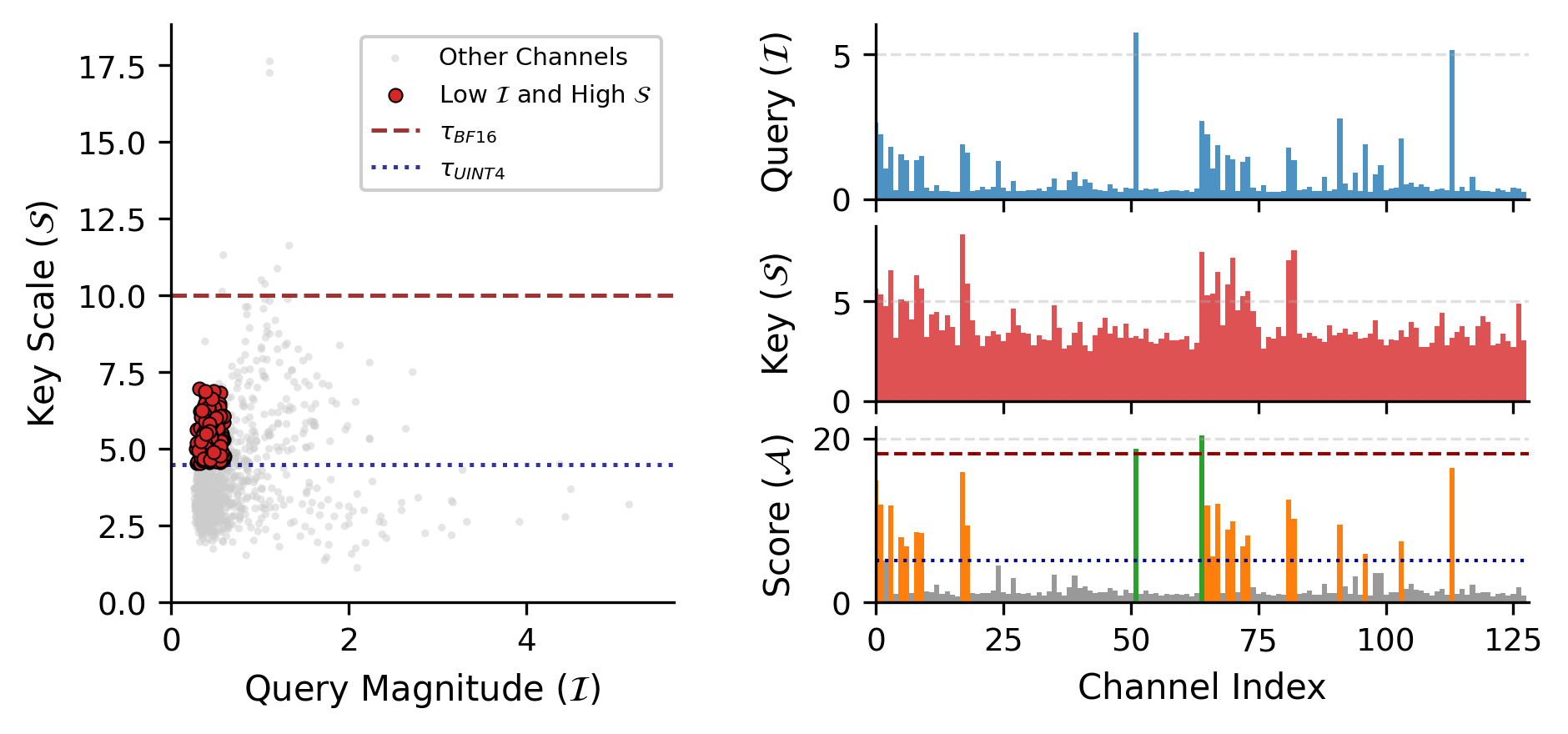
Figure 3: Analysis of Key channel properties on Qwen-2.5-14B-Instruct. Scatter plot of Query magnitude ($\mathcal{I}$) versus Key scale ($\mathcal{S}$); only the product accurately discriminates critical channels.

Consequently, what is required is a composite channel salience metric that encodes both quantization difficulty (via scale) and attention relevance (via query magnitude).

MixKVQ Design and Algorithm

MixKVQ is proposed as a plug-and-play, query-aware mixed-precision quantization method for KV caches. The core insight is to define channel salience as the product $\mathcal{A}_d = \mathcal{I}_d \cdot \mathcal{S}_d$, where $\mathcal{I}_d$ is the mean absolute query activation for channel $d$ (quantifying relevance for the current context) and $\mathcal{S}_d$ is the channel's quantization scale (representing intrinsic quantization sensitivity).

MixKVQ employs a tiered precision allocation: each channel is dynamically assigned to one of three precision levels (BF16, UINT4, or UINT2) based on thresholded salience scores. Channels with high salience are preserved in BF16; moderately salient ones are quantized to UINT4; and the least salient channels to UINT2. A sliding-window buffer ensures periodic update of salience statistics and amortizes computational overhead.

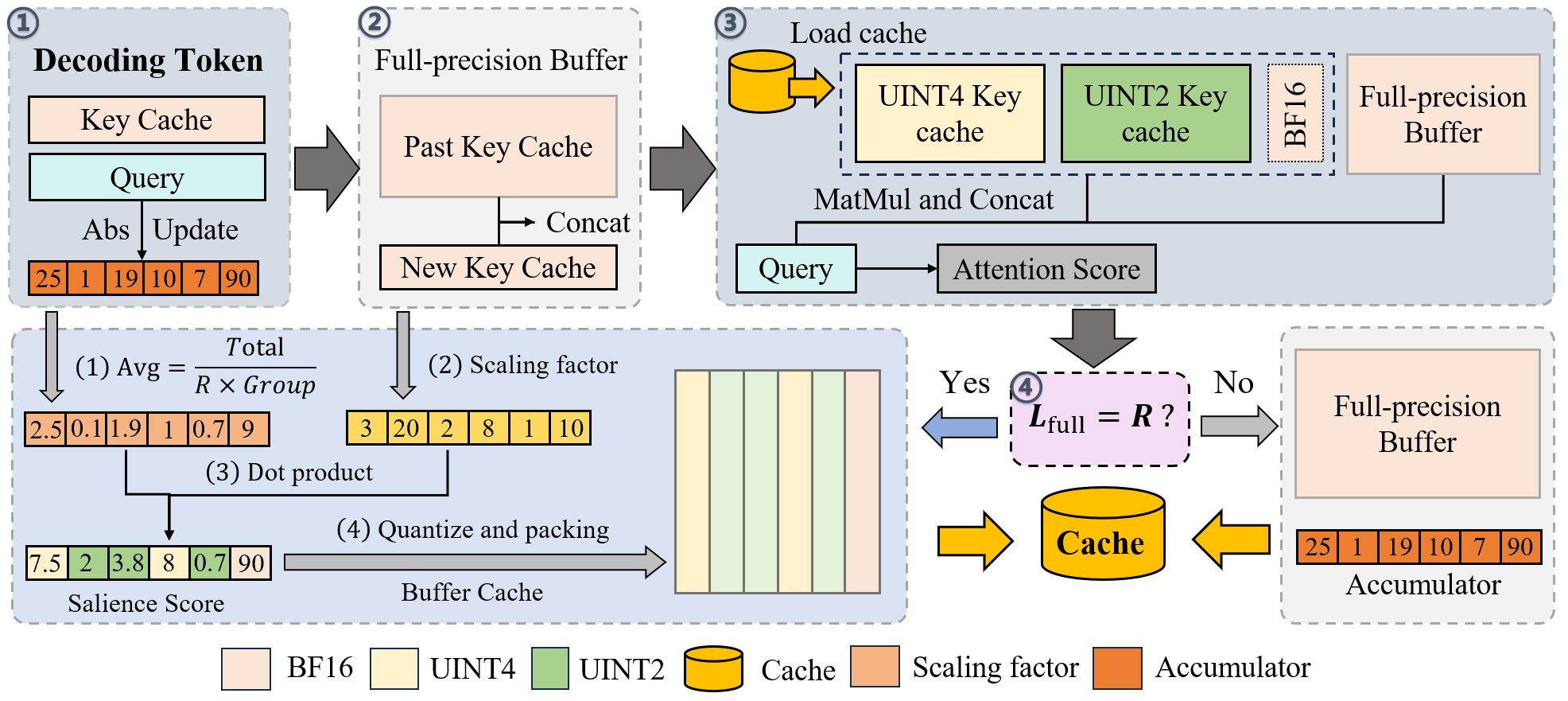
Figure 4: Workflow of MixKVQ. Keys and Values undergo per-channel and per-token quantization, respectively; critical channels are identified and preserved in higher precision via query-aware salience scoring.

For Key cache, this per-channel, query-aware allocation is crucial to identifying outlier dimensions even within layers erroneously classified as non-critical by static heuristics, as visualized in explicit failure analyses of layer-wise methods.

Empirical Results and Numerical Highlights

Extensive evaluation demonstrates that MixKVQ achieves nearly lossless performance (relative to BF16 full-precision inference) at average bit-widths as low as 2.3–2.7 bits, for a broad spectrum of tasks. On the DeepSeek-R1-Distill-Qwen-32B model family, MixKVQ recovers 66.04% average accuracy (BF16: 67.84%) on aggregate complex reasoning benchmarks, outperforming KIVI-2bit by 7.15%. Unlike KVTuner and other mixed-precision schemes, MixKVQ prevents catastrophic accuracy drops even at aggressive memory constraints.

On LongBench, MixKVQ compression to 2.7 bits achieves accuracy within 0.2% of the BF16 baseline on both Mistral-7B and Llama-3.1-8B, consistently outperforming state-of-the-art quantization competitors under equivalent bit budgets.

MixKVQ enables up to 2.25$\times$ increase in supported batch size and 2.63–2.81$\times$ increase in throughput at the same maximum memory consumption, as validated by ShareGPT-style throughput experiments.

Figure 5: Memory usage and throughput comparison between MixKVQ and 16 bit baseline.

Analysis of Channel Selection and Limitations of Previous Mixed-Precision Methods

Detailed failure case analyses reveal that static, layer-wise policies (e.g., KVTuner) are unable to address local outlier features that emerge within channels in otherwise non-critical layers. The query-aware, channel-level mechanism of MixKVQ dynamically captures these outliers, optimizing bit allocation to focus on the true drivers of attention fidelity.

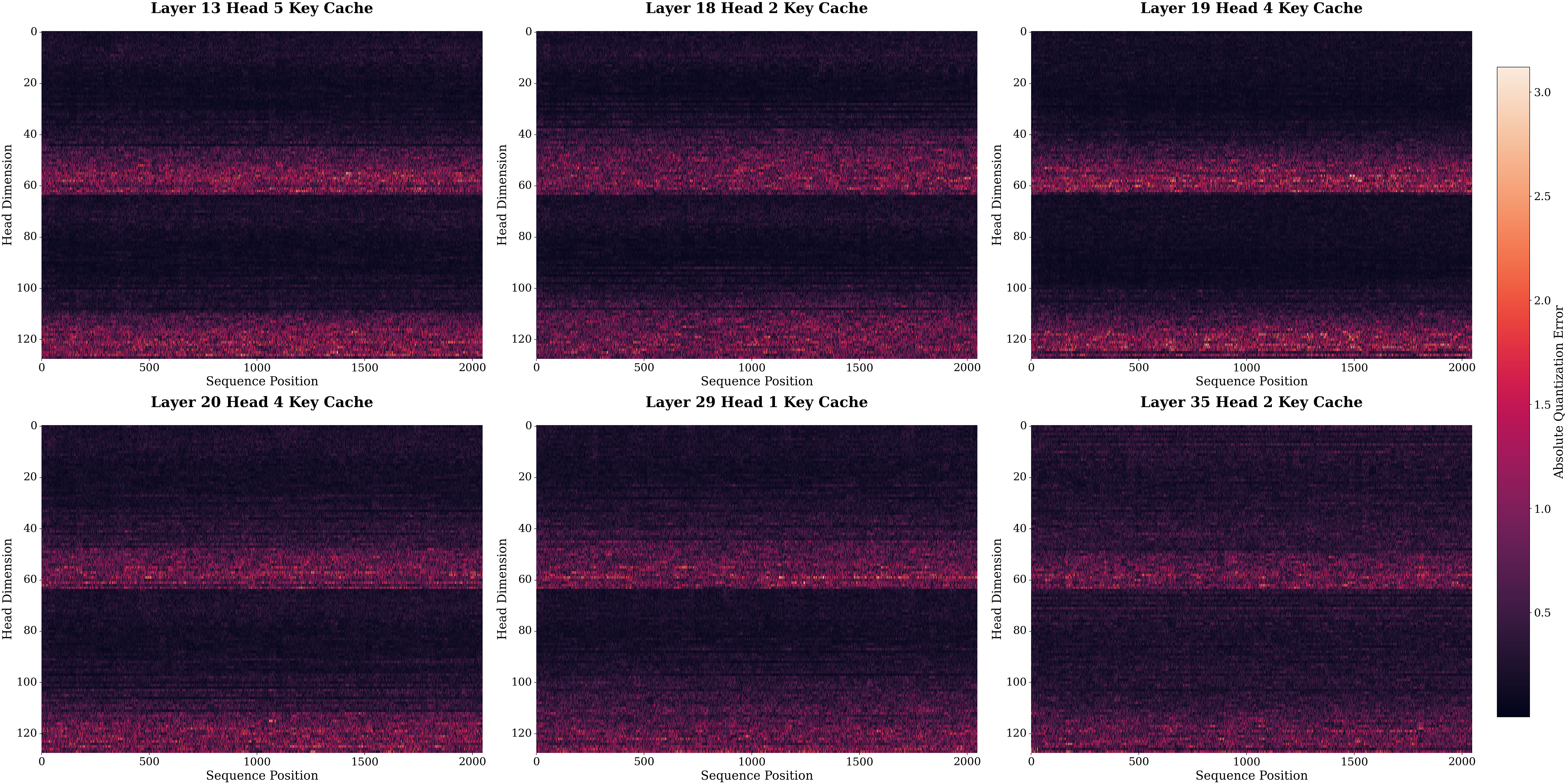
Figure 6: Failure case analysis of the KVTuner method. Outlier features in statically assigned "non-critical" layers result in unmitigated errors under uniform quantization.

Furthermore, Pareto frontier analyses on GSM8K slices confirm MixKVQ's robustness: for a given bit-width budget, it extends the accuracy frontier beyond existing methods, and the selected thresholds and bit allocations exhibit architecture-specific adaptivity.

Figure 7: Pareto frontier of different models with the MixKVQ quantization mode on the 25 data slices of the GSM8K dataset.

Implementation and Practical Implications

MixKVQ introduces moderate computational overheads owing to online channel salience estimation and periodic quantization but amortizes these costs efficiently and is compatible with hardware pipelining and current LLM inference accelerators. The trade-off between residual buffer length and quantization frequency allows practitioners to flexibly balance latency against accuracy and compression.

Critically, the method is orthogonal and complementary to other cache management approaches (e.g., selective eviction, low-rank decomposition, retrieval-oriented frameworks). This plug-and-play attribute supports its immediate adoption in diverse serving stacks and real-world inference systems.

Conclusions

MixKVQ establishes that fixed-error proxies for precision assignment are fundamentally inadequate for extreme low-bit quantization in long-context LLMs. By incorporating both query-driven importance and quantization sensitivity, MixKVQ achieves substantial KV cache compression while preserving reasoning and generation fidelity. The preservation of attention integrity at sub-3-bit operation opens new opportunities for cost-effective deployment of long-context LLMs and sets a new standard for fault-tolerant quantization under constrained resource budgets.

Future research may address dynamic buffer management, specialization to emerging attention mechanisms (e.g., Multi-Head Latent Attention), and deeper integration with memory-aware inference frameworks for further throughput gains.