Assembly Addition Chains (2512.18030v1)

Abstract: In this paper we extend the notion of Addition Chains over Z+ to a general set S. We explain how the algebraic structure of Assembly Multi-Magma over the pairs (S,BB proper subset of S) allows to define the concept of Addition Chain over S, called Assembly Addition Chains of S with Building Blocks BB. Analogously to the Z+ case, we introduce the concept of Optimal Assembly Addition Chains over S and prove lower and upper bounds for their lengths, similar to the bounds found by Schonhage for the Z+ case. In the general case the unit 1 is in set Z+ is replaced by the subset BB and the mentioned bounds for the length of an Optimal Assembly Addition Chain of O is in set S are defined in terms of the size of O (i.e. the number of Building Blocks required to construct O). The main examples of S that we consider through this papers are (i) j-Strings (Strings with an alphabeth of j letters), (ii) Colored Connected Graphs and (iii) Colored Polyominoes.

• The paper introduces a generalized algebraic framework that extends addition chains to arbitrary combinatorial objects and defines the Assembly Index.
• It systematically constructs objects such as strings, colored graphs, and polyominoes using multi-magma structures and binary gluing operations.
• The work establishes bounds on assembly complexity and proves the NP-completeness of computing the Assembly Index for these structures.

Assembly Addition Chains: A General Algebraic Framework

Introduction

The paper "Assembly Addition Chains" (2512.18030) introduces a generalized algebraic framework that extends classical Addition Chains (AC) in $\mathbb{Z}^+$ to arbitrary sets $S$ endowed with combinatorial 'gluing' operations. Leveraging the formalism of Multi-Magma structures, the authors define Assembly Addition Chains (AAC), enabling the recursive construction and indexing of structured combinatorial objects beyond integers, including strings, colored graphs, and polyominoes. This expansion allows the adaptation of integer complexity and optimal representation ideas to new domains and quantifies the combinatorial assembly complexity via the Assembly Index (AI).

Assembly Addition Chains: Generalized Construction

The core innovation is the generalization from integer addition chains to an abstract construction process on non-numeric sets. The authors formalize the idea with Assembly Multi-Magma structures $(S, \circ, BB)$, where $S$ is a set of objects, $BB \subset S$ is the subset of building blocks, and $\circ$ is a binary multivalued operation capturing all possible 'gluings.'

For classical addition chains, the process recursively builds up to $n$ using additions, starting at 1. The generalized version, the AAC, recursively constructs complex objects in $S$ from $BB$ using binary gluing steps, with each chain corresponding to a valid build pathway. This perspective accommodates various discrete assembly spaces beyond $\mathbb{Z}^+$, as long as the underlying operation and blocks are defined. Examples in the paper include:

• j-Strings: Sequences composed from an alphabet of size $j$, with concatenation as the gluing operation.
• Colored Connected Graphs (CCG): Graphs assembled by gluing subgraphs via edge/vertex identification under color constraints.
• Polyominoes: Planar shapes created by combining colored squares.

The generalization is not trivial: whereas addition in $\mathbb{Z}^+$ is unique and associative, gluing in combinatorial objects may yield multiple nonisomorphic results, requiring the Multi-Magma construction.

Figure 1: Multi-Magma structure over the set of Colored Fixed Polyominoes demonstrates generalized binary 'gluing' for complex combinatorial objects.

Optimal Assembly Chains and Assembly Index

Analogous to the minimal-length ACs for integers, the paper defines Optimal Assembly Addition Chains for objects in $S$. The corresponding minimal number of steps needed to assemble an object is its Assembly Index $a(\mathscr{O})$, which generalizes integer additive complexity $\ell(n)$. This quantifies the minimal assembly effort—a deeply structural invariant reflecting the object's composition.

For sets where the decomposition into building blocks and the gluing operation is well-behaved, the Assembly Index is shown to satisfy bounds similar to those for integers (as in Schönhage’s results):

$$\log_2(s(\mathscr{O})) \leq a(\mathscr{O}) \leq s(\mathscr{O}) - 1$$

where $s(\mathscr{O})$ measures the 'size' (number of building blocks) of $\mathscr{O}$. The paper provides further refinements for lower bounds via mapping assembly chains to ordinary integer addition chains, and for upper bounds using structural decompositions such as binary decomposability and 2-piece decomposability.

Figure 2: Assembly Index as a function of string length for all 2-Strings up to length 25 demonstrates the growth and variation of assembly complexity.

Combinatorial Structures: Strings, Graphs, Polyominoes

The approach is concretely illustrated for several significant families:

Strings

For strings, the framework supports both directed and undirected cases. The assembly operations correspond to concatenation (or its symmetric versions), and the combinatorial explosion of possible objects as string length increases is addressed explicitly. The bounds and explicit enumeration clarify the growth of the maximum and minimum Assembly Index as a function of string size and alphabet size, exhibiting quasi-linear, sawtooth progression.

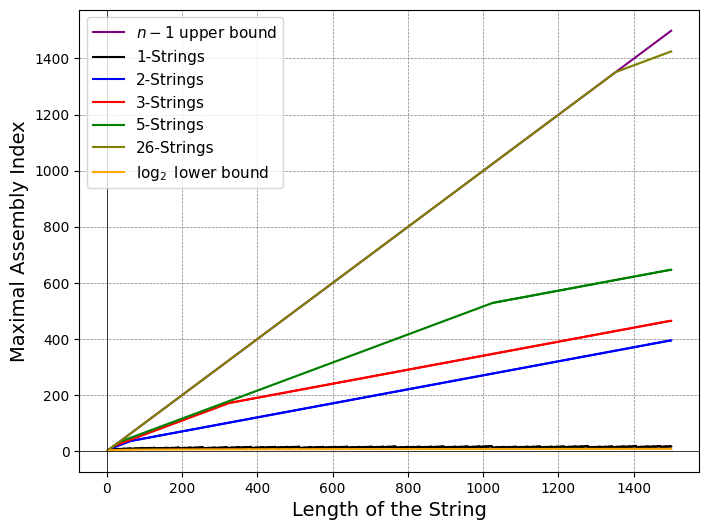
Figure 3: Maximum Assembly Index of $j$-Strings for several $j$; sawtooth behavior reflects combinatorial burst as size grows.

Colored Connected Graphs

For CCGs, the assembly operation is graph gluing, and the building blocks are monochromatic edges. The analysis exploits known decomposition results, including path-decompositions for even-size graphs. The paper derives that all CCGs are 2-piece decomposable, allowing sharp upper bounds for the Assembly Index.

Figure 4: Maximum Assembly Index of Colored Connected Graphs for various numbers of colors highlights dependency on color degree.

Polyominoes

For polyominoes, the assembly process is graph-theoretically transferred to well-defined 'skeletons.' The building blocks are squares, and the assembly exploits bijections to colored graphs, enabling adaptation of the earlier upper bounds.

Figure 5: All Polyominoes of sizes three, four, five, and six, illustrating the exponential growth in the number of assembly-relevant objects.

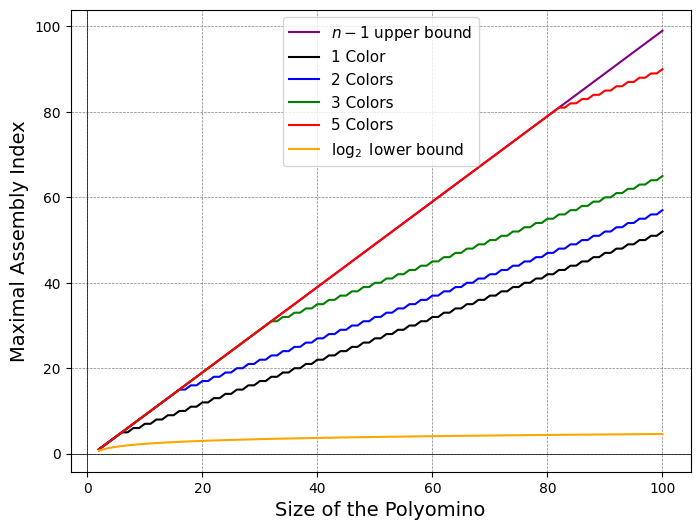
Figure 6: Maximum Assembly Index for Polyominoes as a function of color count shows the complexity explosion with increasing symmetry and color.

Algorithmic Complexity and Computational Intractability

The authors rigorously demonstrate that, as with integer addition chain length, the general problem of computing the Assembly Index is NP-complete. Even for moderate object sizes, brute-force enumeration is infeasible, which justifies the need for sharp analytical bounds and structural reductions. The provided bounds are computationally relevant, offering nontrivial certificates or constraints in practical enumeration tasks.

Theoretical and Practical Implications

The generalization delivered in this paper universalizes the notion of additive complexity, opening a systematic approach for quantifying assembly effort and compressibility for arbitrary combinatorial objects. Potential applications include:

• Combinatorial enumeration: Sharp bounds for counting structures with a given assembly complexity, central to chemical graph enumeration and synthetic pathway design.
• Algorithmic compressibility: Insights into how objects can be minimally represented or built, with implications for data compression and efficient algorithms.
• Structural complexity theory: The AI provides an object-centric complexity measure, enabling the comparative analysis of symmetry, pattern repetition, or regularity.
• Chemical informatics and assembly theory: The framework offers a pathway-based complexity measure highly relevant for quantifying molecular structure complexity.

For instance, the mapping between Assembly Addition Chains and Directed Acyclic Graphs supports formal linkage to assembly pathway enumeration in synthetic chemistry.

Figure 7: Construction of a maximal Assembly Path for a Binary Decomposable object, illustrating the assembly protocol’s DAG structure.

Speculation and Future Research

The introduction of an object-dependent algebraic complexity measure fosters several questions:

• Symmetry-complexity link: Are objects with low Assembly Index necessarily more symmetric? Is there a formal correspondence between AI, automorphism group size, and structural repetition?
• Enumeration of complexity classes: How does the cardinality of assembly universes (the set of objects of a given AI) grow as a function of size, color count, or combinatorial type?
• Extensions to other algebraic structures: Can this paradigm be adapted to partially ordered sets, higher-dimensional complexes, or categorical constructions?
• Algorithmic optimization: Are there efficient heuristics for specific classes (e.g., sparse graphs, restricted polyominoes), or is the general intractability unavoidable?

Conclusion

"Assembly Addition Chains" establishes an algebraically rigorous, broadly applicable extension of addition chain theory to arbitrary combinatorial construction spaces. It offers deep insights into the enumeration and assembly complexity of strings, graphs, and polyominoes, linking combinatorial, algebraic, and computational perspectives. The formalism, connecting construction pathways to graph-theoretical and complexity-theoretic foundations, provides new tools for many domains interested in the minimal synthesis or description of structured objects. This framework is poised for further developments in combinatorics, algorithmic information, chemistry, and theoretical computer science.