Spherical Voronoi: Directional Appearance as a Differentiable Partition of the Sphere (2512.14180v1)

Abstract: Radiance field methods (e.g. 3D Gaussian Splatting) have emerged as a powerful paradigm for novel view synthesis, yet their appearance modeling often relies on Spherical Harmonics (SH), which impose fundamental limitations. SH struggle with high-frequency signals, exhibit Gibbs ringing artifacts, and fail to capture specular reflections - a key component of realistic rendering. Although alternatives like spherical Gaussians offer improvements, they add significant optimization complexity. We propose Spherical Voronoi (SV) as a unified framework for appearance representation in 3D Gaussian Splatting. SV partitions the directional domain into learnable regions with smooth boundaries, providing an intuitive and stable parameterization for view-dependent effects. For diffuse appearance, SV achieves competitive results while keeping optimization simpler than existing alternatives. For reflections - where SH fail - we leverage SV as learnable reflection probes, taking reflected directions as input following principles from classical graphics. This formulation attains state-of-the-art results on synthetic and real-world datasets, demonstrating that SV offers a principled, efficient, and general solution for appearance modeling in explicit 3D representations.

• The paper introduces the Spherical Voronoi representation, a differentiable partition of the sphere that overcomes limitations of spherical harmonics and Gaussians.
• It leverages adaptive temperature mapping to model both diffuse and specular effects, achieving higher PSNR and robustness in experimental evaluations.
• The method seamlessly integrates with radiance field and rendering pipelines, enabling efficient, real-time, high-fidelity appearance modeling.

Spherical Voronoi: Explicit, Differentiable Partitioning for Directional Appearance

Introduction and Problem Formulation

The paper "Spherical Voronoi: Directional Appearance as a Differentiable Partition of the Sphere" (2512.14180) addresses a foundational challenge in novel view synthesis and physically-based rendering: accurate and efficient modeling of directional appearance, particularly view-dependent phenomena such as specular highlights and reflections, within radiance field frameworks. Traditional approaches such as Spherical Harmonics (SH) and Spherical Gaussians (SG) offer either computational efficiency or high-frequency localization, but not both simultaneously. SH are globally supported and easy to optimize but struggle with high-frequency artifacts, as demonstrated by the presence of Gibbs phenomena in reconstructions of sharp features.

Figure 1: SH reconstruction of localized specular "glints" is affected by Gibbs artifacts, making it impractical for high-frequency appearance modeling.

The practical limitations of both SH and SG for explicit, real-time appearance modeling motivate the introduction of the Spherical Voronoi (SV) representation. SV partitions the sphere into smooth, adaptive, learnable regions, enabling stable optimization while supporting both low- and high-frequency directional effects.

Spherical Voronoi Representation

SV represents spherical functions by a set of sites on the unit sphere, each associated with a function value and a temperature parameter controlling the sharpness of its partition. The output is a weighted blend via a softmax over the dot products of the sites with the queried direction. This construction yields an explicit, non-overlapping decomposition of the sphere, avoiding the "competition" and optimization instability endemic to SG and Spherical Betas (SB).

Figure 2: SV bases construct a domain partition with learnable Voronoi sites, covering the sphere adaptively.

A key feature is the tunability of temperature: low values yield broad, smoothly varying functions, while high temperatures result in sharp, discontinuous partitions suitable for mirror-like reflection modeling.

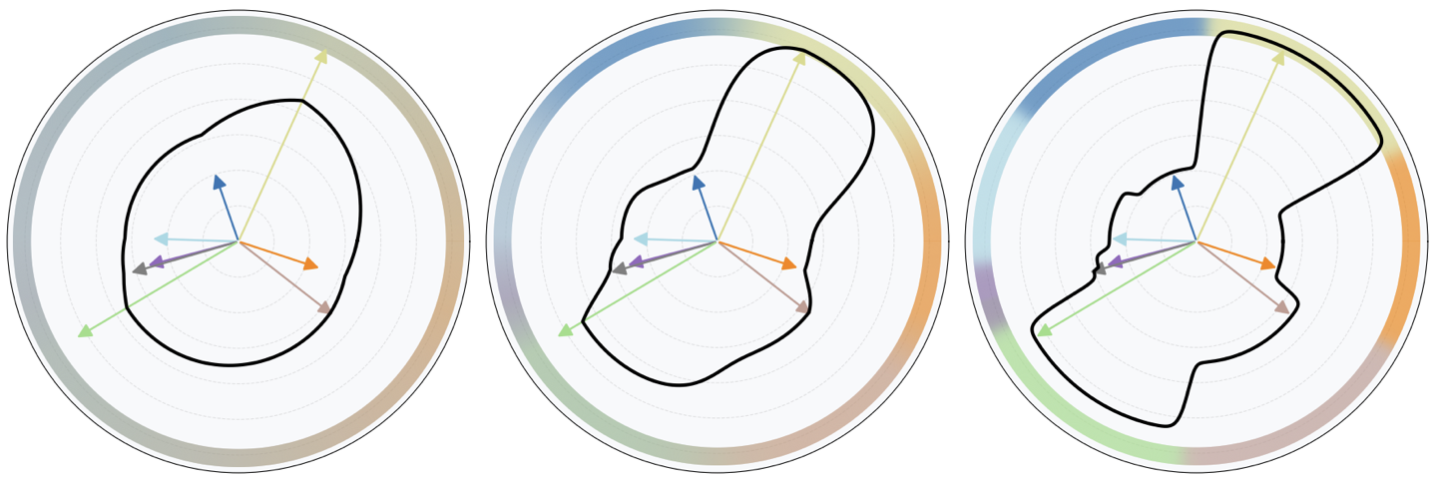
Figure 3: Increasing $\tau$ causes the SV basis to transition from smooth averaging to crisp, sharp partitions, supporting both diffuse and specular effects.

Quantitative and qualitative experiments confirm SV's superior convergence behavior and robustness against local minima compared to prior bases. Repeated optimization trials from random initializations demonstrate consistently higher PSNR and reliable recovery of ground-truth functions.

Figure 4: SV fitting is more robust and consistently obtains higher PSNR compared to SH, SG, and SB, as evidenced by multiple trial outcomes.

Integration with Radiance Fields and Rendering Pipelines

SV extends naturally to parameterizing the view-dependent component of gaussian-based radiance fields, as well as modeling spatially varying reflectance by employing learnable light probes. Each gaussian primitive in splatting-based pipelines is augmented with SV parameters; for reflection modeling, SV is used for local probes distributed in 3D space and for far-field cubemap representation.

Figure 5: SV-based deferred rendering pipeline utilizes geometry and attribute buffers, blending probe-driven near-field and cubemap-driven far-field illumination for final shading.

The explicit SV representation, when used either for view-directional radiance ($f_{SV}(\omega)$) or reflection ($f_{SV}(\omega_r)$), is highly expressive. SV probes can be learned end-to-end and adaptively focus on regions of the scene with complex near-field interactions, clustering around reflective surfaces and enabling high-fidelity, spatially varying appearance estimation.

Experimental Results and Quantitative Evaluation

The paper presents comprehensive quantitative comparisons with leading radiance field and splatting baselines across standard synthetic and real datasets. SV consistently achieves top-tier PSNR, SSIM, and LPIPS metrics across all tested scenarios and particularly excels in reflection-heavy benchmarks.

Figure 6: SV models outperform state-of-the-art methods, including Ref-GS, 3DGS-DR, and various neural field and splatting approaches, yielding sharper branch reflections and more coherent specular effects across datasets.

Ablations demonstrate that the removal of SV probe components or the explicit material parameters (i.e., roughness) degrades the sharpness and coherence of specular reflections, confirming the centrality of SV's partitioning and adaptive temperature mapping.

Figure 7: Ablation study highlights that full SV formulation is necessary for preserving fine appearance details—removing reflections or probes leads to blur and loss of coherence.

Probe dynamics during training validate that SV-probes migrate towards spatial regions of high specular energy, effectively capturing localized directional illumination:

Figure 8: Learnable SV probes cluster around strongly reflective regions during optimization, capturing complex local interactions.

Efficiency and Quality Tradeoffs

With careful engineering, SV evaluation can be accelerated by restricting the softmax computation to direction-dependent local candidate sets via cubemap-based partitioning. Hyperparameter tuning allows balancing kernel capacity and speed, with diminishing returns beyond moderate candidate set sizes.

Practical and Theoretical Implications

SV provides a framework for interpretable, explicit, differentiable appearance modeling that is suitable for radiance fields, rendering, inverse rendering, and novel view synthesis. Its adaptive decomposition of the sphere allows stable optimization even under sparse supervision and is agnostic to the underlying rendering pipeline (MLP, splat, probe-based, deferred shading).

By outperforming even neural decoders in explicit probe-based reflection modeling, SV demonstrates that explicit, parametric representations can supersede deep implicit models in both accuracy and interpretability. This opens avenues for efficient real-time rendering pipelines and facilitates seamless integration into classical physically-based graphics frameworks.

Practically, SV enables robust, high-quality rendering of complex, glossy, or highly reflective scenes without requiring heavy MLP inference. Theoretically, it demonstrates that differentiable domain partitioning can unify far-field and near-field appearance modeling under a single, scalable representation, potentially informing future AI-driven rendering architectures and appearance learning paradigms.

Conclusion

The Spherical Voronoi framework represents a paradigm shift in explicit appearance modeling for directional functions on the sphere. By leveraging adaptive, differentiable partitions with tunable sharpness, SV surpasses classical and neural-based methods in both radiance and reflection modeling, demonstrating state-of-the-art performance across benchmarks and applicability to varied rendering pipelines. Its interpretable, efficient, and fully explicit parameterization suggests future research directions in scalable, hybrid representations for graphics and vision, and can inform the design of next-generation AI-powered rendering and inverse rendering systems.