Random matrix theory of sparse neuronal networks with heterogeneous timescales (2512.12767v1)

Abstract: Training recurrent neuronal networks consisting of excitatory (E) and inhibitory (I) units with additive noise for working memory computation slows and diversifies inhibitory timescales, leading to improved task performance that is attributed to emergent marginally stable equilibria [PNAS 122 (2025) e2316745122]. Yet the link between trained network characteristics and their roles in shaping desirable dynamical landscapes remains unexplored. Here, we investigate the Jacobian matrices describing the dynamics near these equilibria and show that they are sparse, non-Hermitian rectangular-block matrices modified by heterogeneous synaptic decay timescales and activation-function gains. We specify a random matrix ensemble that faithfully captures the spectra of trained Jacobian matrices, arising from the inhibitory core - excitatory periphery network motif (pruned E weights, broadly distributed I weights) observed post-training. An analytic theory of this ensemble is developed using statistical field theory methods: a Hermitized resolvent representation of the spectral density processed with a supersymmetry-based treatment in the style of Fyodorov and Mirlin. In this manner, an analytic description of the spectral edge is obtained, relating statistical parameters of the Jacobians (sparsity, weight variances, E/I ratio, and the distributions of timescales and gains) to near-critical features of the equilibria essential for robust working memory computation.

• The paper establishes that training noise induces an inhibitory core–excitatory periphery motif, which enhances working memory performance.
• It employs a supersymmetry-based random matrix theory to derive explicit spectral edge conditions linking network connectivity statistics with stability.
• Empirical analysis confirms that heterogeneous inhibitory timescales produce a Jacobian spectrum that clusters near the marginal stability line.

Random Matrix Theory of Sparse Neuronal Networks with Heterogeneous Timescales

Introduction and Context

This work develops a random matrix framework for analyzing the stability and dynamics of recurrent excitatory-inhibitory (E/I) neural networks, specifically those trained for working memory tasks characterized by discrete attractor transitions. The central finding motivating the analysis is that additive noise during network training induces an inhibitory core -- excitatory periphery motif, paralleled by a broad and heavy-tailed distribution of inhibitory synaptic timescales, resulting in Jacobian matrices whose spectra accumulate near the marginal stability line, thereby facilitating robust working memory performance.

The analysis addresses the gap in understanding how these emergent, highly structured sparse Jacobians determine the spectral properties critical for network dynamics—going significantly beyond classic dense, i.i.d., or even block-structured random matrix models by incorporating sparsity, block constraints, and elementwise timescale/gain heterogeneity. An analytic theory is developed using field-theoretic (supersymmetry-based) techniques for the Hermitized ensemble, yielding explicit conditions for the support and edge of the spectrum in terms of empirical network statistics.

Discrete Attractors, Working Memory, and Emergent Motifs

Working memory tasks are implemented through input-driven transitions between discrete attractors in state space. In the delayed match-to-sample paradigm, the RNN encodes sequential binary cues, with network states hopping across a series of attractors (fixed points) encoding past input history (Figure 1). Robust performance is achieved if these fixed points are marginally stable—stable enough to withstand noise and delay, yet sufficiently close to instability to enable rapid, controlled transitions upon new cue arrival.

Figure 1: Input-driven transitions between discrete attractors in a delayed match-to-sample task mediated by a recurrent E/I rate network.

Empirically, networks trained with additive noise and learnable timescales self-organize such that:

• The excitatory population's outbound synaptic weights are pruned to near-zero, while inhibition is strong and sparse (Figures 2 and 3).
• Inhibitory timescales become substantially slower and more heterogeneous than excitatory ones, reflecting biological cortex statistics (Figure 2).
• Jacobian spectra around operating points display a distinct geometry: a real-valued bar (excitatory block modes) and a complex inhibitory blob whose edge approaches the stability boundary, with the proximity governed predominantly by inhibitory timescale distribution and synaptic gain statistics (Figures 2 and 6).

  Figure 3: Emergent inhibitory core -- excitatory periphery network architecture and corresponding block-structured Jacobian eigenvalue spectra after noise-driven training.

  

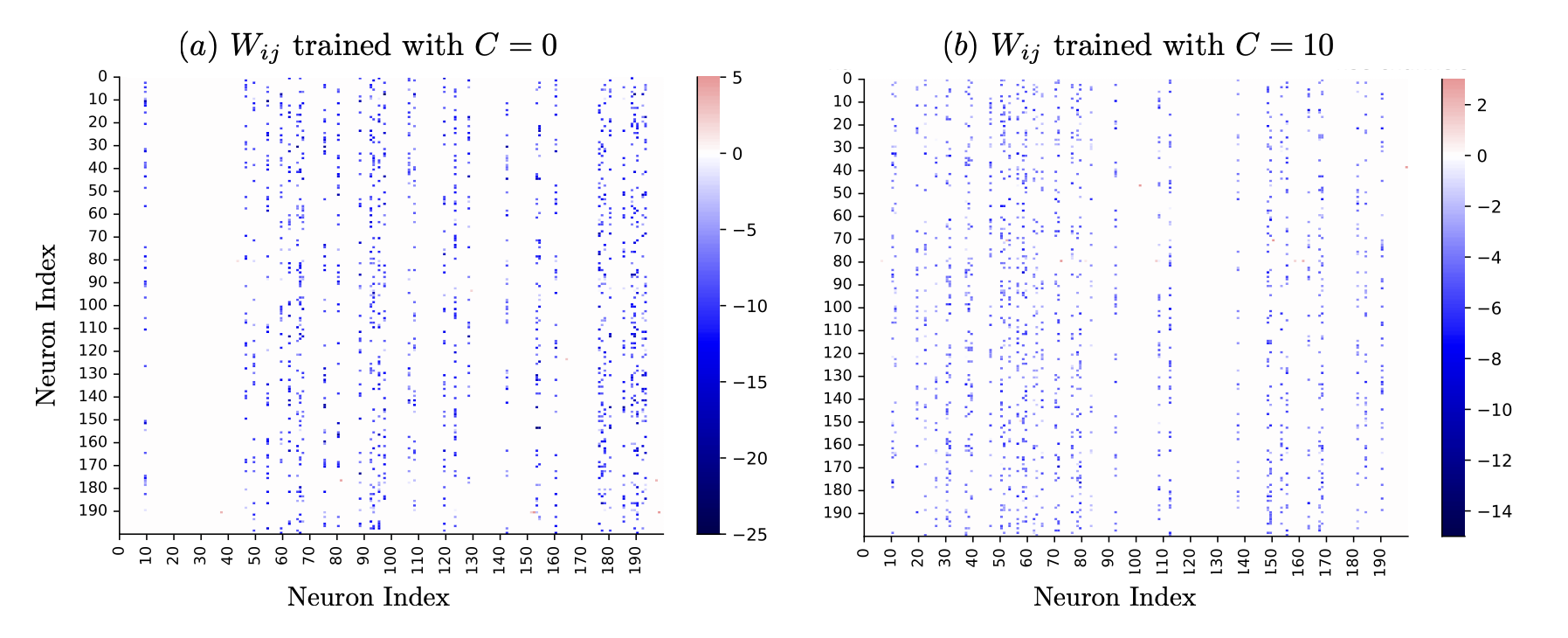
  Figure 4: Typical trained synaptic weights confirm suppression of excitatory outputs and sparsity in the inhibitory core.

  

  Figure 2: Heterogeneous distributions for synaptic timescales and activation gains, with inhibitory population showing extensive rightward skew in $\tau$ after noise-driven training.

Statistical Description of the Trained Jacobian Ensemble

The post-training network connectivity motivates a sparse, non-Hermitian random matrix ensemble for the Jacobian $J$ at each attractor:

$J = \mathcal{T}^{-1}(-I + W \mathcal{H}^*)$

where $\mathcal{T}$ is the diagonal of decay timescales and $\mathcal{H}^*$ is diagonal gain. $W$ is partitioned into E/I blocks, but after training, only the inhibitory columns retain significant (though sparse) connections. Consequently, $J$ is essentially block upper-triangular:

• The excitatory diagonal yields the bar at locations $\{-1/\tau_{E,i}\}$.
• The inhibitory block, with sparse connections, broad $\tau$ and $h$ distributions, yields the complex blob whose edge determines stability.

Empirical analysis of the trained weights and degrees (Figure 5), as well as timescale/gain fits (Figure 2), justifies modeling with:

• Erdős–Rényi sparse graphs in inhibitory core, with Gaussian-distributed weights,
• Beta-distributed $\tau_{I}$ and $h_{I}$,
• Tunable inhibitory fraction $f$.

  Figure 5: Statistical analysis validates Gaussianity and sparsity assumptions for the inhibitory weight matrix elements and binomial-like connection degree distributions.

Supersymmetry-Based Random Matrix Theory for Spectral Analysis

To analyze this ensemble, the authors apply a supersymmetry-based statistical field theory framework. This involves:

• Hermitizing the spectrum (Girko's method) and representing the relevant Green's function as a Gaussian integral over complex commuting (bosonic) and Grassmann (fermionic) variables,
• Averaging over ensemble disorder in weights, timescales, and gains,
• Deploying the Fyodorov-Mirlin superintegral decoupling to render the model analytically tractable in $N \to \infty$ limit,
• Reducing the spectral properties to solutions of a set of self-consistent saddle-point equations.

The key analytic result is a precise spectral edge condition for the inhibitory blob in the $z$-plane:

$$k_I \sigma^2 \mathbb{E}_h[h^2] \, \mathbb{E}_{\tau_I}\left[\frac{1}{|z \tau_I + 1|^2}\right] = 1$$

where $k_I$ is inhibitory mean degree, $\sigma^2$ the inhibitory weight variance, and distributions for $h$ and $\tau_I$ taken from trained networks.

Figure 6: In the homogeneous $\tau_I$ case (all timescales identical), the inhibitory spectral edge is circular and its vicinity to $\Re \lambda = 0$ (stability boundary) is controlled by $k_I \sigma^2 \mathbb{E}_h[h^2]$.

Dependence of Spectral Features on Biological Parameters

Increasing the mean and variance of the inhibitory timescale distribution systematically moves the inhibitory blob toward the stability boundary, favoring longer relaxation times and enhanced working memory (Figures 7 and 8). Furthermore:

• The real axis bar (excitatory block) position is purely set by $\{\tau_{E,i}\}$.
• For broad, heterogeneous $\tau_I$, the inhibitory spectral edge nontrivially deforms away from circles, but is always confined by convexity/Jensen's inequality, with rightmost approach to instability occurring on the real axis.
• The spectral edge is not determined by the overall E/I population fraction, but by the statistical properties of the active inhibitory block (Figure 7).

These findings causally link structural features learned during training (sparse inhibitory motifs, prolonged inhibitory timescales, magnitude of training noise, degree distribution) to specific spectral and thus dynamical signatures required for high-performance computation.

Figure 7: Validation of the theoretical spectral edge against numerically measured spectra for empirical Jacobians obtained from networks trained under differing noise conditions; the edge is captured accurately by Eq. (1).

Figure 8: Altering the distribution shape of inhibitory timescales controls the inhibitory edge location, enabling regimes arbitrarily close to instability—key for temporal memory.

Theoretical and Practical Implications

Analytically, this work generalizes classical random neural network spectral results to the regime of sparse, block-structured, and heterogeneously scaled synaptic matrices—beyond any classic Ginibre/circular law setting. The integrable field-theoretic paradigm employed is extendable to various constrained random systems of interest in computational neuroscience, physics, and ecology. The derived edge condition establishes a direct functional relationship between microscopic network training statistics and the dynamical operating regime.

On the neuroscience side, these results demonstrate how realistic training protocols (involving noise and plastic synaptic timescales) can drive networks to the optimal regime for temporal memory: the spectrum piles up at the brink of instability, with a wide array of slow modes naturally produced by biological heterogeneity. The findings concretely justify the idea that slow inhibition is a structural and functional substrate for robust working memory, rather than a mere byproduct of biological variability.

Further, since the functional role of the excitatory periphery (now largely dynamically silent) is shifted toward mediating transient amplification via non-normality in the full-block Jacobian, future work is poised to extend this spectral analysis to examine dynamical responses and memory capacity—potentially linking these observations to broader questions of computation in complex biological and artificial systems.

Conclusion

This study establishes a rigorous analytic and statistical correspondence between the sparse, noise-trained connectivity motifs present in working-memory-capable E/I RNNs and their fine-grained spectral properties. The authors' field-theoretic framework yields closed-form spectral edge conditions involving only measurable network statistics, and the model accurately predicts spectral features observed in trained networks. The analysis elucidates how intentionally engineered or evolving timescale heterogeneity and circuit-level sparsity robustly implement the edge-of-instability regime optimal for temporal integration and attractor-based memory in high-dimensional neural systems.