An Efficient Variant of One-Class SVM with Lifelong Online Learning Guarantees (2512.11052v1)

Abstract: We study outlier (a.k.a., anomaly) detection for single-pass non-stationary streaming data. In the well-studied offline or batch outlier detection problem, traditional methods such as kernel One-Class SVM (OCSVM) are both computationally heavy and prone to large false-negative (Type II) errors under non-stationarity. To remedy this, we introduce SONAR, an efficient SGD-based OCSVM solver with strongly convex regularization. We show novel theoretical guarantees on the Type I/II errors of SONAR, superior to those known for OCSVM, and further prove that SONAR ensures favorable lifelong learning guarantees under benign distribution shifts. In the more challenging problem of adversarial non-stationary data, we show that SONAR can be used within an ensemble method and equipped with changepoint detection to achieve adaptive guarantees, ensuring small Type I/II errors on each phase of data. We validate our theoretical findings on synthetic and real-world datasets.

• The paper introduces SONAR, a strongly convex one-class SVM variant, demonstrating rigorous guarantees on controlling Type I and Type II errors in streaming data.
• It leverages Random Fourier Features to efficiently approximate Gaussian RBF kernels, achieving O(d) time and space complexity in online settings.
• The adaptive variant SONARC employs changepoint detection to ensure robust lifelong learning and transfer in non-stationary environments.

An Efficient Variant of One-Class SVM with Lifelong Online Learning Guarantees

Introduction and Motivation

The paper "An Efficient Variant of One-Class SVM with Lifelong Online Learning Guarantees" (2512.11052) addresses the problem of online outlier detection in non-stationary data streams, focusing on stringent guarantees for both Type I (false positives) and Type II (false negatives) errors. The work is motivated by applications such as IoT anomaly detection, where computational constraints preclude traditional batch methods and environments are subject to temporal shifts. The study critically examines kernel-based One-Class SVM (OCSVM) methods, highlighting their inefficiencies and suboptimal Type II error under non-stationarity. It then introduces SONAR, a strongly convex SGD-based OCSVM variant, and SONARC, an adaptive version equipped with changepoint detection, yielding favorable theoretical and empirical properties in both stationary and non-stationary regimes.

Strongly Convex Regularization and Algorithmic Framework

The classical OCSVM objective is extended by introducing a regularized, strongly convex loss functional:

$$F(w,\rho) = \frac{1}{2}(\|w\|_2^2 + \rho^2) - \lambda \rho + \mathbb{E}_{X \sim P_X}[(\rho - w^T X)_+]$$

where $w \in \mathbb{R}^d$ and $\rho \in \mathbb{R}$ are model parameters after Random Fourier Features (RFF) kernelization. The strong convexity in $(w, \rho)$ enables rigorous analysis for the convergence rates of the online SGD iterates. The algorithm SONAR operates in a single-pass streaming setting, where at each time $t$, it updates model parameters on a fresh data point. RFFs are leveraged to approximate the Gaussian RBF kernel, yielding efficient updates and evaluation in $O(d)$ time and space.

The new objective directly admits unbiased stochastic subgradients in the streaming setting, enabling theoretically optimal last-iterate convergence rates. This distinguishes it from batch dual OCSVM or representer-theorem based methods, which incur quadratic or cubic cost in retrospective data access.

Statistical Guarantees: Type I and Margin Bounds

The paper establishes the following central statistical guarantees for SONAR and its optimal solution:

• Type I Control: For any fixed $\lambda \in [0,1]$, the learned classifier achieves $\mathbb{P}_{X \sim P_X}(w^T X < \rho) < \lambda$ for the parameter minimizer and, with high probability, for the SGD iterate provided a slightly shrunken threshold.
• Margin Lower Bound: The solution margin $r_\lambda = \rho_\lambda / \|w_\lambda\|_2$ is at least as large as the minimal support hemisphere margin, $r^*$, of the data after kernelization. Empirically and theoretically, SONAR tends to yield larger rejection regions for near-boundary outliers than standard OCSVM, reducing Type II error for alternatives close to the decision boundary.
• Improved (Faster) Convergence: Due to strong convexity, last-iterate guarantees for SGD converge as $O(\frac{\log T}{T})$ (in probability), which is sharper than the $O(T^{-1/2})$ rate for the original objective.
• Refined Transfer Learning Bounds: Under mild non-stationarity, the generalization error and margin of SONAR benefit from past performance---that is, the error and margin on a new phase are upper/lower bounded by those attained on the previous distribution, plus a vanishing adaptation term in the new phase.

This set of guarantees is a strict improvement over what is achievable for standard convex (but not strongly convex) OCSVM, both in sample complexity and learning-theoretic transfer under shift.

Adaptive Changepoint Detection and SONARC

In settings where the data-distribution changes are adversarial or abrupt, lifelong SGD can suffer. Here, the adaptive algorithm SONARC monitors an ensemble of SONAR solvers with staggered restarts (at dyadic intervals). A principled hypothesis test on the discrepancy between current and recent SGD iterates is used for on-the-fly changepoint detection, ensuring restarts only when the decision boundary has demonstrably shifted.

• Theoretical Safety Guarantee: Changepoints are only detected (with high probability) if there is a change in the population minimizer, avoiding unnecessary resets due to inconsequential support drift.
• Oracle-Competitive Adaptivity: On each stationary phase, SONARC provably matches the guarantees of an oracle with perfect knowledge of shift locations, ensuring small Type I and II errors and maximal margins within each segment, up to logarithmic factors.

Computational Complexity and Scalability

A key practical strength is the linear scaling of SONAR and SONARC in both training and query time. With Random Fourier Features dimension $d = O(D \log(D / \delta))$ (where $D$ is input dimension), total memory and computation are $O(d)$ and $O(T d)$, respectively. In comparison, naïve online kernel OCSVM would require $O(TD)$ memory and incur $O(T^2 D)$ (or worse) time due to kernel matrix maintenance.

Experimental Validation

Synthetic and Controlled Shifts

Across a variety of synthetic scenarios, including stationary and shifting mixture models, SONAR and SONARC empirically demonstrate:

• Sharply controlled online Type I error in all regimes.
• Rapid adaptation to sudden distributional changes with negligible performance loss compared to an oracle restarting algorithm.
• Superior or comparable margin growth and acceptance region geometry relative to SGD-OCSVM baselines.

  Figure 1: Online Type I Error, margin, and final decision boundaries of SONAR and SGD-OCSVM on stationary synthetic data.

  

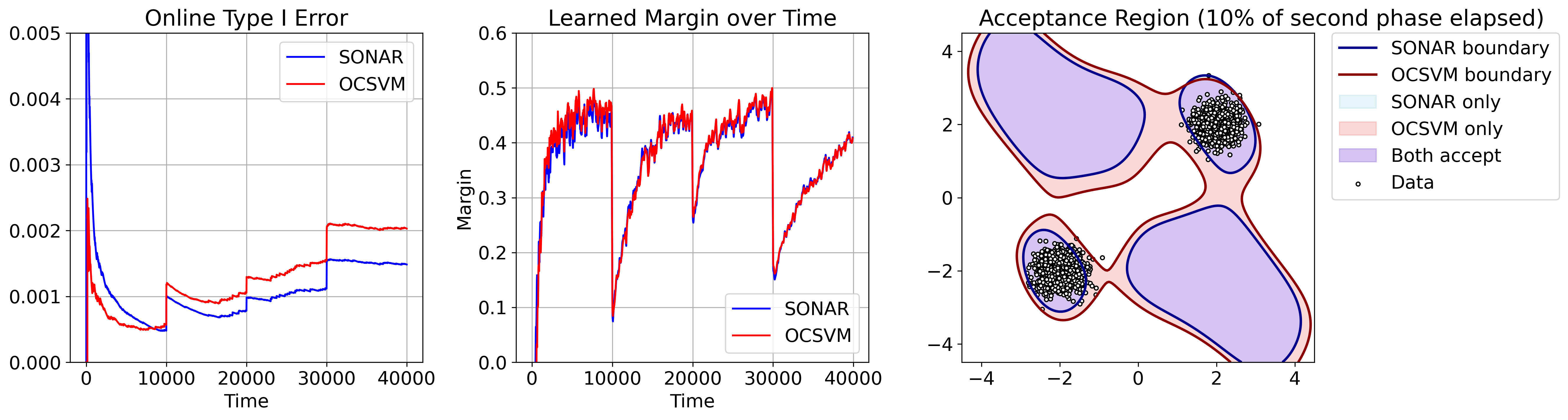
  Figure 2: Online Type I Error, margin, and acceptance region snapshots for SONAR vs. SGD-OCSVM under non-stationarity.

Lifelong Transfer

SONAR retains previous margin and Type I error performance post-shift, demonstrating robust transfer learning without explicit resets. This aligns with the theoretical adaptation guarantees.

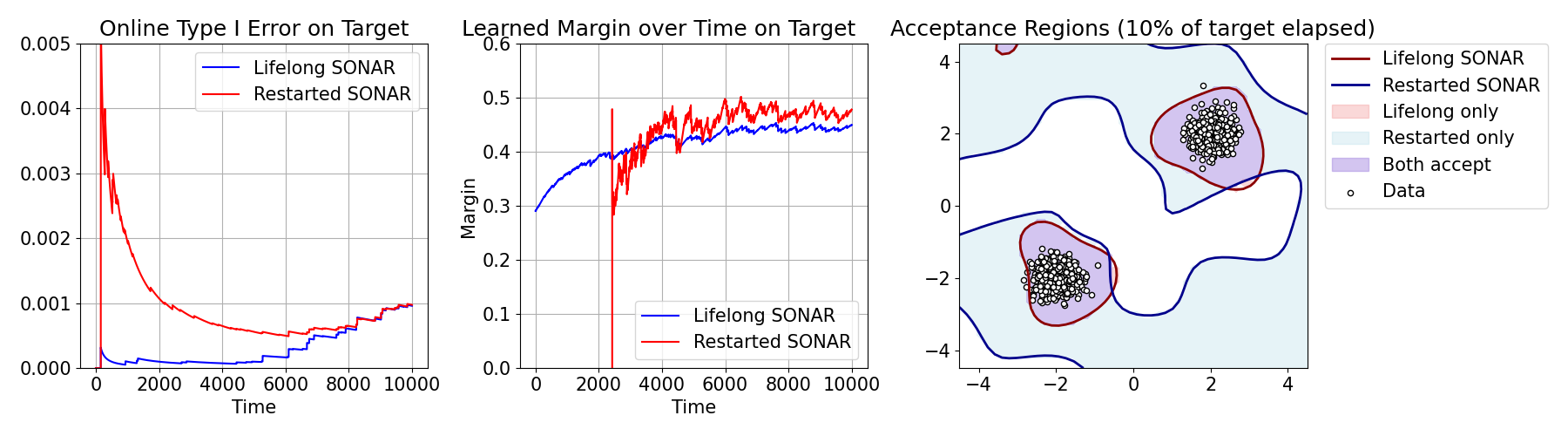
Figure 3: Margin plots and acceptance region visualization in lifelong transfer; SONAR maintains competitive margin with rapid adaptation post-shift.

Adversarial and Multiple Shifts

SONARC outperforms simple non-restarting or naïve changepoint approaches in environments with frequent adversarial changepoints, closely matching oracle adaptation and avoiding unnecessary recomputation.

Figure 4: Online Type I Error and smoothed margin for multiple changepoint experiments; SONARC closely tracks oracle restart strategy.

Comparison with Off-the-shelf Changepoint Detectors

SONARC's logic for restarting is strictly more selective than generic detectors, only invoking restarts when the outlier boundary changes—thus avoiding unnecessary resets on benign distribution support drift.

Figure 5: Scatterplot, margin, and acceptance regions showing off-the-shelf changepoint detectors are over-conservative compared to SONARC.

Real-World IoT and Time Series

SONAR and SONARC are benchmarked on the Skoltech Anomaly Benchmark (SKAB) and Aposemat IoT-23, using only initial normal data and ignoring labels for outliers. Key findings include:

• Type I control is consistently within the target $\lambda$ throughout the stream.
• Type II error is minimized during critical periods by SONARC, especially early in new phases.
• SONARC triggers a plausible number of restarts, aligning with ground-truth distributional periods.

  Figure 6: SKAB results—online Type I and II error, and learned margin; SONARC outperforms OCSVM and SONAR in adaptive Type II error reduction.

Implications and Future Directions

The results demonstrate that strongly convex modifications of one-class classification objectives enable robust, efficient, and provably adaptive online anomaly detection, even under strong distributional drift. The capacity for rapid transfer learning and phase-aware adaptivity positions SONAR and SONARC as attractive baselines for deployment in streaming, resource-constrained scenarios, such as IoT security monitoring, with formal guarantees on generalization and computational resource usage.

Looking forward, several promising avenues present themselves:

• Direct Type II Analysis: While current guarantees are margin-based, future work may establish sharp, distribution-dependent bounds on missed outlier rates for various classes of alternative distributions.
• Robustness to Labeled Feedback: Extending the framework to incorporate rare, possibly delayed, labeled outlier instances could further enhance practical efficacy.
• Extensions to Other Kernels and Function Classes: Generalizing the theoretical machinery to alternative feature mappings and non-Hilbertian settings.

Conclusion

The study systematically advances the theory and practice of online outlier detection by bridging strong statistical guarantees with computational tractability. The proposed strongly convex framework and its adaptive variant provide new tools for lifelong learning in non-stationary environments, aligning theoretical rigor with empirically validated performance in both synthetic and real-world settings.