Scaling Behavior of Discrete Diffusion Language Models (2512.10858v1)

Abstract: Modern LLM pre-training consumes vast amounts of compute and training data, making the scaling behavior, or scaling laws, of different models a key distinguishing factor. Discrete diffusion LLMs (DLMs) have been proposed as an alternative to autoregressive LLMs (ALMs). However, their scaling behavior has not yet been fully explored, with prior work suggesting that they require more data and compute to match the performance of ALMs. We study the scaling behavior of DLMs on different noise types by smoothly interpolating between masked and uniform diffusion while paying close attention to crucial hyperparameters such as batch size and learning rate. Our experiments reveal that the scaling behavior of DLMs strongly depends on the noise type and is considerably different from ALMs. While all noise types converge to similar loss values in compute-bound scaling, we find that uniform diffusion requires more parameters and less data for compute-efficient training compared to masked diffusion, making them a promising candidate in data-bound settings. We scale our uniform diffusion model up to 10B parameters trained for $10^{22}$ FLOPs, confirming the predicted scaling behavior and making it the largest publicly known uniform diffusion model to date.

• The paper demonstrates that discrete diffusion language models, particularly with uniform diffusion, scale efficiently under compute constraints.
• It introduces the generalized interpolating discrete diffusion (GIDD) framework to explore various noise types and optimize hyperparameter tuning.
• It finds that optimal batch sizes and learning rates scale predictably with training tokens, offering actionable insights for compute-efficient model design.

Here is an essay about the paper "Scaling Behavior of Discrete Diffusion LLMs" (2512.10858):

Introduction

The paper "Scaling Behavior of Discrete Diffusion LLMs" investigates the scaling laws of discrete diffusion LLMs (DLMs) compared to autoregressive LLMs (ALMs). DLMs offer a fundamentally different approach to language modeling, where the generative process is decomposed into a series of denoising steps. This paper explores the scaling behavior of these models, focusing on key hyperparameters such as noise type, batch size, and learning rate. The findings indicate that DLMs, particularly those employing uniform diffusion, show promising scaling characteristics that could make them competitive with ALMs at larger scales.

Diffusion Process and Methodology

Discrete diffusion models operate by reversing a corruption process that gradually adds noise to data, with the objective to denoise and generate coherent sequences. The paper introduces generalized interpolating discrete diffusion (GIDD), which provides a framework for studying different noise types, including masked, uniform, and hybrid-noise diffusion models. The authors propose a novel hybrid noise method that interpolates between masking and uniform diffusion using signal-to-noise ratio (SNR) as the transition metric, arguing that SNR offers a more natural parameterization than time.

Key Findings on Scaling Behavior

The paper's core analysis revolves around the scaling behavior of DLMs across various noise configurations and model sizes. The research demonstrates that while all noise types converge to similar loss values under compute-constrained conditions, uniform diffusion emerges as more parameter-efficient, requiring fewer data for compute-optimal training. This characteristic positions uniform diffusion as a viable candidate in data-limited environments. The paper confirms these scaling behaviors by training DLMs up to 10 billion parameters, finding that the resulting models align well with the predicted scaling laws.

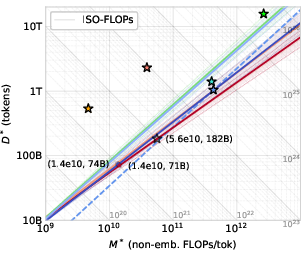
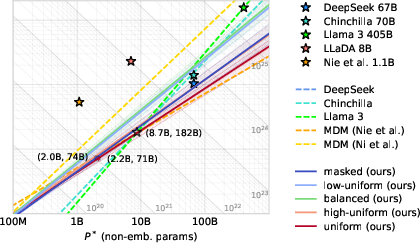
Figure 1: Compute-optimal token-to-parameter ratios as a function of model size can vary significantly for different training objectives.

Optimal Hyperparameters

Significant insights are gained regarding the optimal hyperparameters for training DLMs. The findings suggest that the optimal batch size scales quasi-linearly with training tokens, while the optimal learning rate is dependent on batch size rather than model size. These hyperparameters must be meticulously tuned at each scale to achieve compute efficiency. Moreover, the paper identifies a close relationship between batch sizes and step counts that achieve similar loss levels, implying that both need to be carefully balanced for optimal performance.

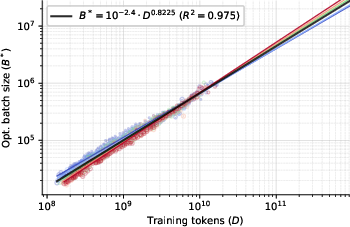
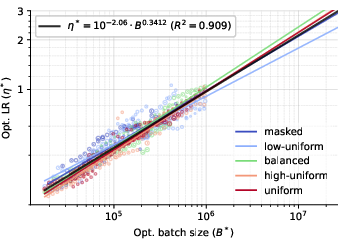
Figure 2: The optimal batch size $B^*$ of discrete diffusion model scales as a power law of training tokens, and the optimal learning rate $\eta^*$ follows a power law in batch size.

Practical Implications and Future Directions

The research presents DLMs, particularly those leveraging uniform noise, as a compelling alternative to the prevailing ALM paradigm due to their ability to scale effectively with compute, suggesting a re-examination of model design choices in large-scale language modeling. This could lead to the development of models that are not only computationally efficient but also capable of generating rich and diverse text outputs. The next steps should involve further exploration of DLMs in diverse datasets and applications, including tasks outside traditional language modeling.

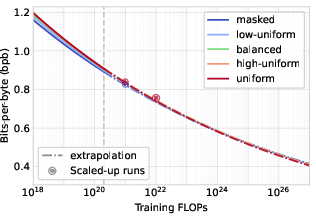
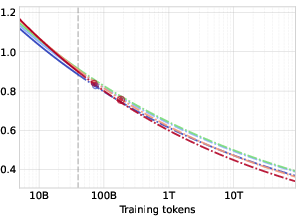
Figure 3: Scaling laws for different noise types indicate competitive scaling in compute-bound settings for DLMs.

Conclusion

In summary, this paper contributes a comprehensive examination of the scaling behavior of discrete diffusion LLMs, indicating that uniform diffusion in particular supports more parameter-heavy, compute-efficient scaling than previously realized. The paper paves the way for future work on optimizing DLM architectures and training regimes, potentially surpassing the capabilities of current state-of-the-art autoregressive models in large-scale settings. As AI models continue to grow in scale and complexity, understanding and leveraging these scaling laws will be crucial in efficiently utilizing computational resources.