Diffusion differentiable resampling (2512.10401v1)

Abstract: This paper is concerned with differentiable resampling in the context of sequential Monte Carlo (e.g., particle filtering). We propose a new informative resampling method that is instantly pathwise differentiable, based on an ensemble score diffusion model. We prove that our diffusion resampling method provides a consistent estimate to the resampling distribution, and we show by experiments that it outperforms the state-of-the-art differentiable resampling methods when used for stochastic filtering and parameter estimation.

• The paper introduces a diffusion resampling technique that employs a pathwise differentiable diffusion model to transform weighted samples into an unweighted set.
• The method integrates gradient-based optimization in SMC frameworks by leveraging a forward-time Langevin SDE initialized at the target distribution.
• Numerical experiments demonstrate lower KL divergence and enhanced filtering accuracy compared to methods like Gumbel-Softmax and optimal transport techniques.

An Analysis of "Diffusion differentiable resampling" (2512.10401)

Introduction

The paper "Diffusion differentiable resampling" introduces a novel differentiable resampling method specifically designed for sequential Monte Carlo (SMC) frameworks. The innovation centers around leveraging a diffusion model, which stands in contrast to conventional resampling techniques that typically impart discrete randomness, thereby complicating gradient-based parameter estimation in state-space models (SSMs). This work posits that the use of diffusion resampling not only mitigates these difficulties but also enhances computational efficiency and consistency.

Methodology Overview

At the core, the diffusion resampling method is predicated on a pathwise differentiable technique using a diffusion model. This model transforms weighted samples into an unweighted set while ensuring consistency with the original target distribution. It employs a forward-time Langevin stochastic differential equation (SDE) initialized at the target distribution $\pi$, eventually converging to a user-chosen reference distribution (e.g., Gaussian).

The paper underscores the ensemble score diffusion model, an approach to construct an informative resampler. Crucially, this method instantaneously provides pathwise derivatives, promoting seamless integration with gradient-based optimization schemes, prominently in filtering and parameter estimation tasks within SMC samplers.

Numerical Results

The authors validate the efficacy of their diffusion resampling method through extensive computational experiments, comparing it against existing differentiable resampling strategies. Key performance indicators include filtering accuracy, parameter estimation precision, and computational overhead.

Notably, the diffusion resampling consistently outperforms Gumbel-Softmax, soft resampling, and optimal transport (OT) methods when tasked with filtering and gradient-based parameter estimation challenges. For instance, in a linear Gaussian SSM, the results show substantial gains in both accuracy—reflected in lower KL divergence—and computational stability against alternative approaches.

Figure 1: Average running times of diffusion resampling and OT.

Discussion of Implications

The theoretical contributions of the paper extend to a thorough exploration of the error bounds associated with diffusion resampling, enhancing our understanding of the interplay between sample size, diffusion time, and resampling error modeled under a Wasserstein metric framework.

Practically, the introduction of diffusion resampling could redefine standard practices within SMC implementations, particularly in scenarios demanding high precision in parameter estimation. The technique’s potential to stabilize gradient estimates makes it extraordinarily beneficial in deep learning models that encapsulate stochastic components, offering a path forward for integrating expressive neural network architectures with SMC methodologies.

Future Directions

The paper hints at several promising avenues for future exploration. Key among these is enhancing the robustness of the SDE solvers used for diffusion processes, optimizing the trade-offs between computational load and resampling precision. Developing adjoint SDE techniques adapted for diffusion resampling could further unlock computational efficiencies.

Continued investigation into the use of different reference distributions within the diffusion framework represents another domain of exploration, with anticipated benefits of further reducing bias and variance in resampling tasks.

Conclusion

In sum, the paper offers a compelling advancement in the space of differentiable resampling mechanisms, successfully bridging theoretical and application frontiers. By integrating diffusion processes within the SMC resampling paradigm, the authors provide researchers with a refined tool, one that holds the promise of improved performance across a suite of statistical modeling tasks in machine learning and beyond.

Figure 2: Root mean square errors of predictions based on learnt prey-predator models over independent runs. The best results go to the first two columns from diffusion resampling.

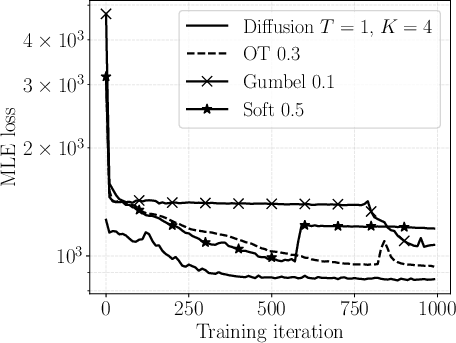
Figure 3: Loss traces (median over all runs) for training the prey-predator model. The training enabled by the diffusion resampling achieves the lowest and stablest.

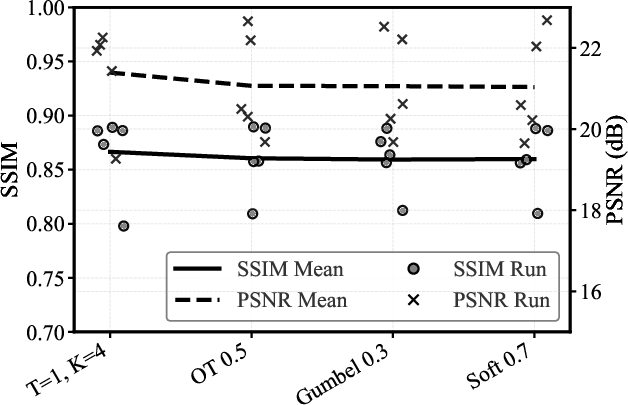
Figure 4: Mean prediction SSIM and PSNR for the best (by mean) model configuration of each resampler.

Figure 5: Qualitative comparison of learnt pendulum dynamics against the ground truth.