Supervised learning pays attention (2512.09912v1)

Abstract: In-context learning with attention enables large neural networks to make context-specific predictions by selectively focusing on relevant examples. Here, we adapt this idea to supervised learning procedures such as lasso regression and gradient boosting, for tabular data. Our goals are to (1) flexibly fit personalized models for each prediction point and (2) retain model simplicity and interpretability. Our method fits a local model for each test observation by weighting the training data according to attention, a supervised similarity measure that emphasizes features and interactions that are predictive of the outcome. Attention weighting allows the method to adapt to heterogeneous data in a data-driven way, without requiring cluster or similarity pre-specification. Further, our approach is uniquely interpretable: for each test observation, we identify which features are most predictive and which training observations are most relevant. We then show how to use attention weighting for time series and spatial data, and we present a method for adapting pretrained tree-based models to distributional shift using attention-weighted residual corrections. Across real and simulated datasets, attention weighting improves predictive performance while preserving interpretability, and theory shows that attention-weighting linear models attain lower mean squared error than the standard linear model under mixture-of-models data-generating processes with known subgroup structure.

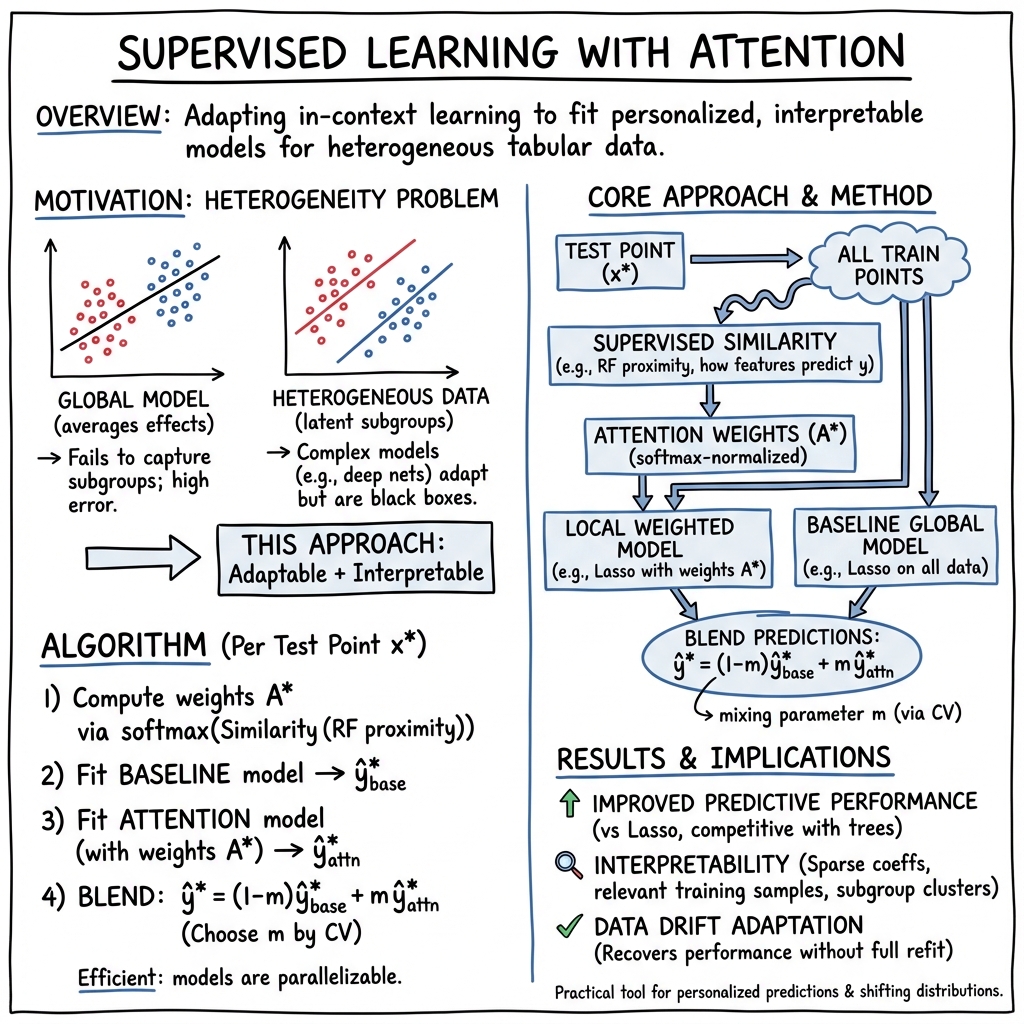
• The paper proposes an innovative attention-weighted supervised learning framework that integrates local and global model fits using supervised similarity.
• The methodology employs random forest proximity and ridge importance to compute per-test-point attention weights, achieving significant reductions in mean squared error.
• The approach enhances interpretability and adapts to data drift by blending personalized local predictions with conventional global models.

Supervised Learning with Attention: An Expert Synthesis

Introduction

"Supervised learning pays attention" (2512.09912) introduces a generalizable framework for integrating attention mechanisms, directly inspired by in-context learning and neural transformer models, into classical supervised learning applied to tabular data. The approach achieves flexible, context-sensitive, and interpretable model fitting by enabling per-test-point personalization without explicit pre-specification of clusters or subgroups. The methodology—termed attention-weighted supervised learning—leverages supervised similarity estimation via random forest proximity or ridge importance, and supports a blend between global and local modeling governed by a mixing hyperparameter optimized via cross-validation.

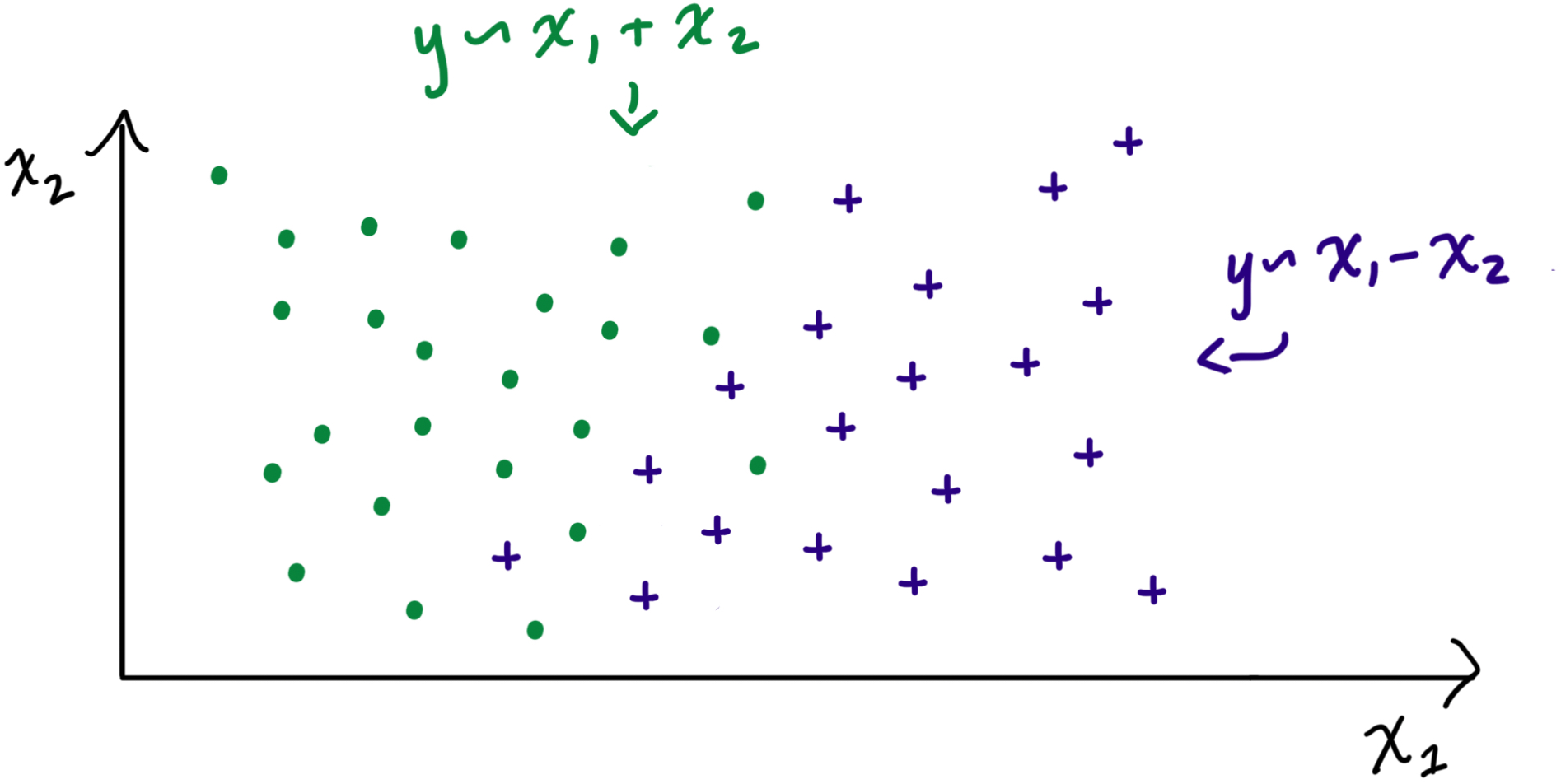
Figure 1: Toy example of a dataset with two features, $x_1$ and $x_2$, where the true model depends on the values of the features.

The framework is rigorously motivated both theoretically and empirically. Strong numerical results are reported, and the implications extend from improving predictive accuracy and interpretability on heterogeneous tabular datasets to practical scenarios such as data drift correction, time series, and spatial prediction.

Methodology

Attention-weighted Model Fitting

The method proceeds as follows (see Figure 2): for each prediction, attention weights reflecting supervised similarity between the test observation and the training set are computed. These weights, derived from random forest proximity or a diagonally-weighted ridge metric, emphasize training points most predictive for the target outcome. Subsequently, a locally-weighted model (e.g., lasso, boosting) is fit using these weights. The prediction is then a convex combination of the global model and the personalized local model, with mixing $m \in [0,1]$ selected by cross-validation. This controls variance and limits overfitting as the number of fitted models increases.

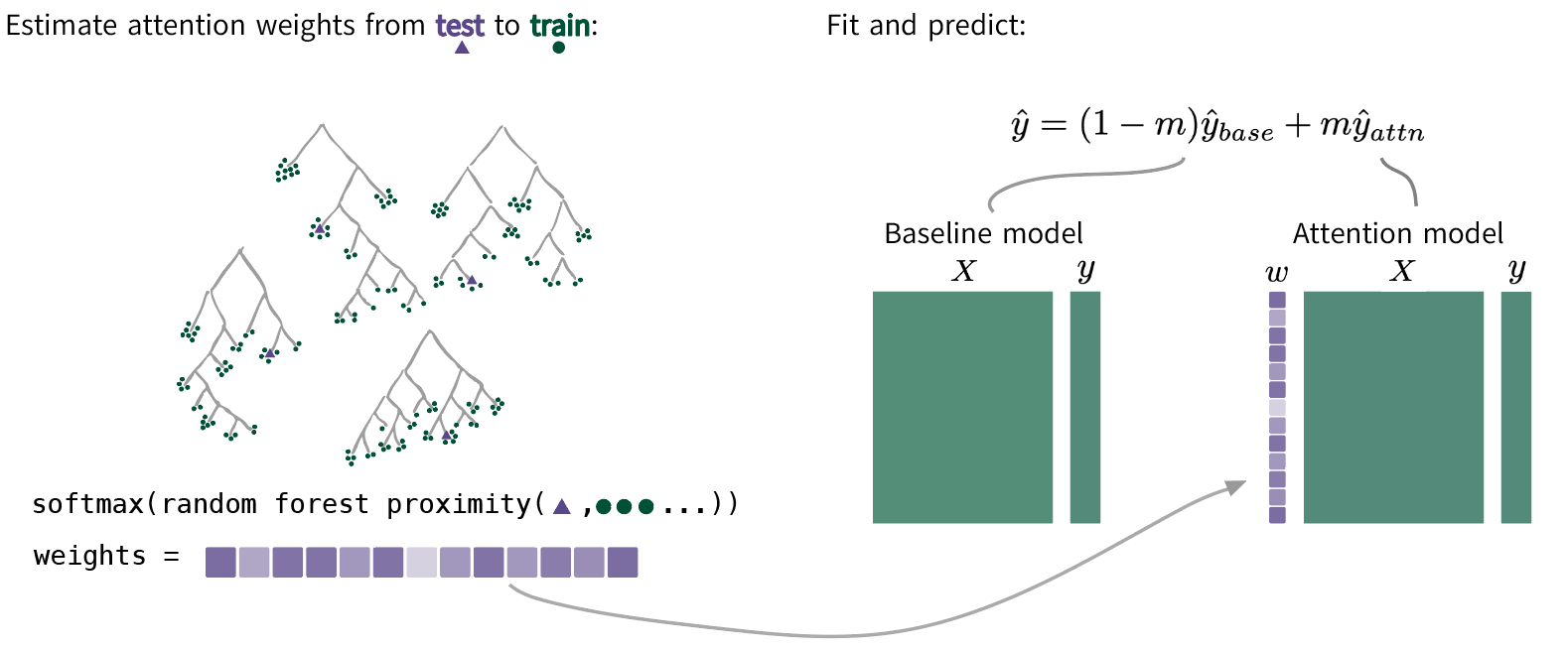
Figure 2: Pipeline for attention-weighted supervised learning, integrating random forest-based similarity with blending of local and global regression estimates.

Formally, for each test input $\bm{x}^*$, attention-derived weights $w^*$ over $\bm{X}$ enable a test-specific weighted fit:

$$\hat{y}^* = (1 - m) \hat{y}^*_\text{global} + m \hat{y}^*_\text{local}.$$

The method extends naturally to other learners (e.g., LightGBM, XGBoost), time series (via contextual features), and spatial data (by leveraging neighborhood features).

Empirical Evaluation

The paper benchmarks attention-lasso and attention-boosted learners on both real and simulated datasets, comparing against lasso, LightGBM, XGBoost, random forest, and KNN. Across 12 UCI tabular datasets, attention-lasso consistently outperforms standard lasso and matches more complex models in terms of predictive mean squared error (see Figure 3).

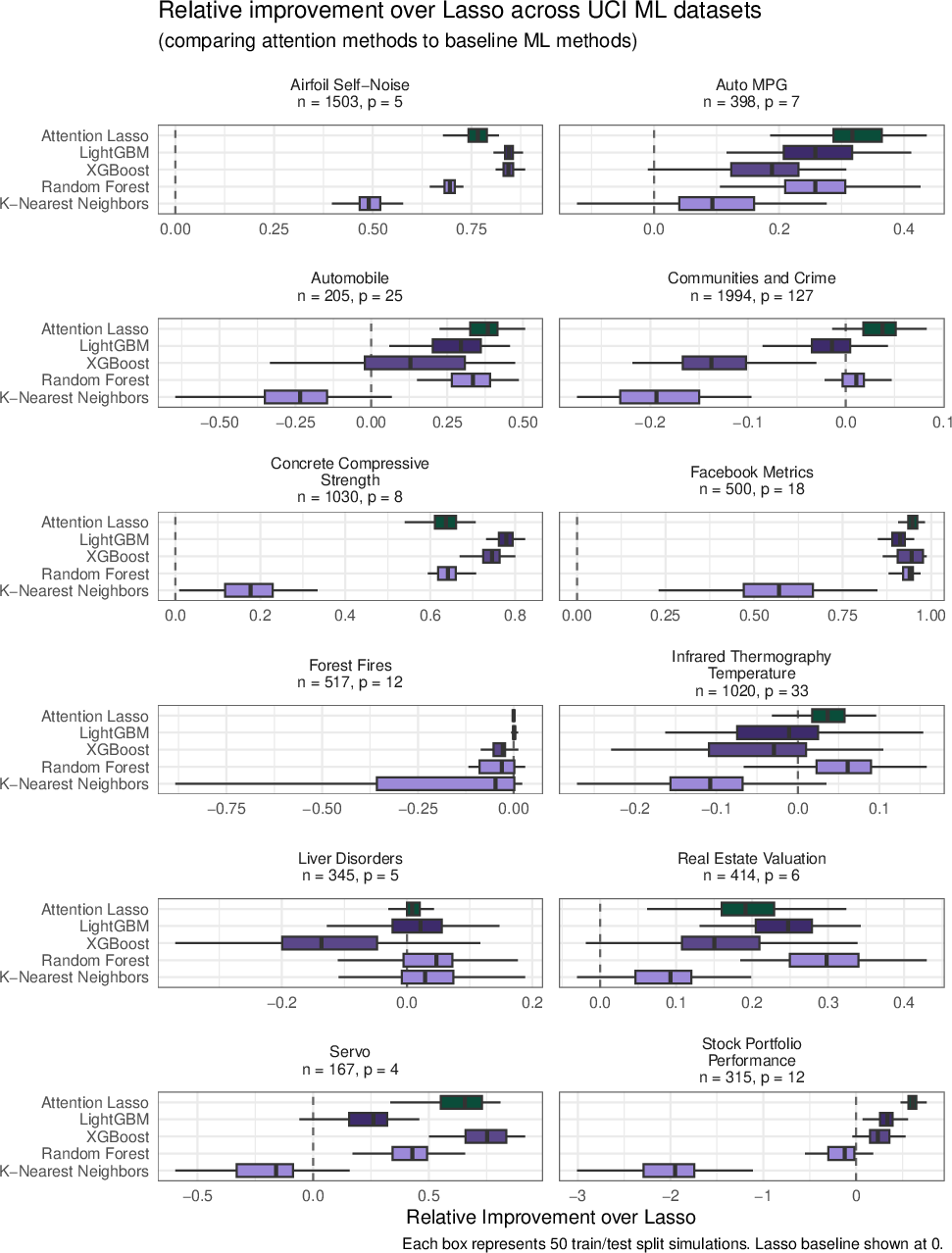
Figure 3: Attention-lasso delivers robust improvements in predictive accuracy compared to lasso, boosting, forest, and KNN across multiple real datasets.

Simulation scenarios encompassing continuous coefficient variation, discrete subgroup structure, high-dimensionality, and overlapping soft clusters further validate the method (see Figure 4). The results quantify mean squared error reductions and demonstrate the method's robustness to varying degrees of latent heterogeneity.

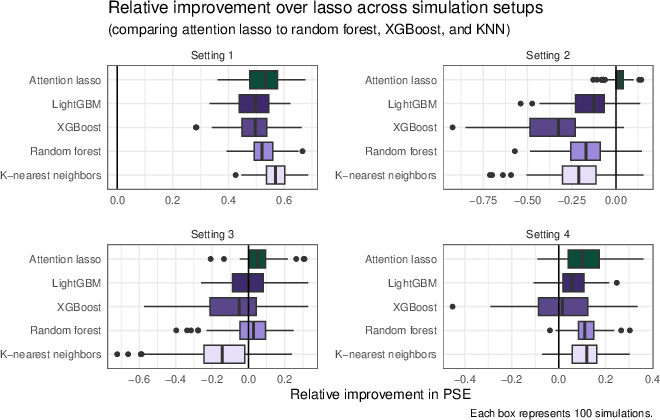
Figure 4: Simulation results exhibiting consistent gains for attention-weighted models across diverse heterogeneity scenarios.

Interpretability & Model Diagnostics

The interpretability of attention-weighted models is preserved via coefficient sparsity (in the case of lasso) and feature importance analysis (for boosting methods). Coefficient vectors for each test point are clustered to reveal latent subgroup structure. Coefficient clustering visualizations on real datasets expose heterogeneity patterns in feature-response relationships (Figure 5).

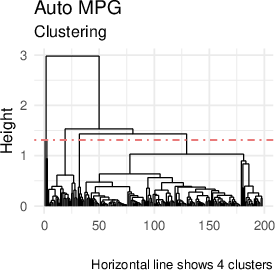
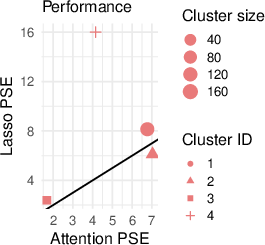
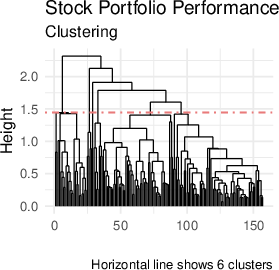
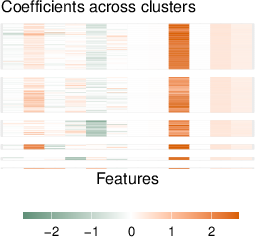
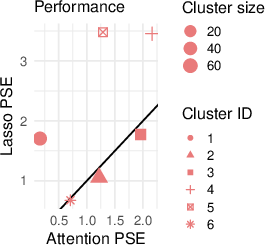
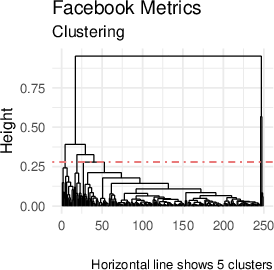
Figure 5: Coefficient clustering shows interpretable subgroup patterns across test points in the Auto MPG, Stock Portfolio, and Facebook datasets.

Feature importance clustering within attention-boosted models exposes subgroup-specific predictive variables, supporting fine-grained data characterization, and diagnostic insight (Figure 6).

Figure 6: Clustered feature importances for the Automobile dataset modelled with attention-boosted ensembles evidence multiple latent data regimes.

Computational Considerations

Although fitting a per-test-point model increases computational load, the process is embarrassingly parallel and comparable to leave-one-out cross-validation in complexity. For tree-based learners, an approximate variant is provided that utilizes attention-weighted responses at terminal nodes, negating the need for refitting full models.

Figure 7: Comparison of LightGBM variants reveals that attention-weighted models with shallow trees retain performance, mitigating overfitting and supporting model interpretability.

Adaptation to Data Drift and Longitudinal Scenarios

The framework addresses prediction under covariate shift (data drift), a frequent real-world challenge, by applying attention-weighted adaptation of residuals without refitting the full model. Residual correction using recent adaptation data recovers much of the performance lost to drift—a substantial practical improvement demonstrated in simulation (Figure 8).

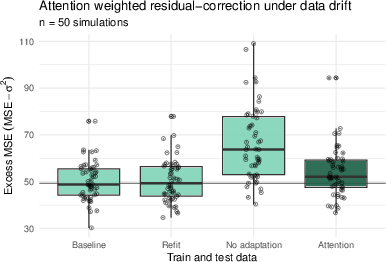
Figure 8: Under significant covariate drift, attention-based residual correction nearly matches the performance of fully refitted models.

Applications in time series and spatial data leverage lagged features and local neighborhood context, respectively, for personalized regression fitting, further supporting its versatility.

Theoretical Results

Under a mixture-of-models data generating process, attention-lasso is shown to reduce both asymptotic prediction error and coefficient bias relative to global lasso fitting. Specifically, the attention mechanism upweights training points from the same latent group, resulting in estimators closer to the true local parameter. The reduction in mean squared error is precisely characterized, with analytical bounds dependent on cluster separability under supervised similarity metrics. These results generalize to attention-weighted variants of kernel regression and locally weighted regression, with enhancements in model regularization and feature selection.

Implications and Future Directions

This research advances the interface between deep learning-inspired techniques and classical interpretable statistical modeling. It shows that in-context attention, a cornerstone of transformer architectures, can be "ported" to tabular modeling to yield personalized, interpretable, and competitive predictions. Notably, attention-weighted models circumvent the need for manual or unsupervised clustering—allowing the underlying supervised similarity structure to drive local adaptation.

Potential future work includes:

• Extension to high-dimensional treatment effect estimation (e.g., R-learner and causal inference).
• Joint optimization of attention weights and predictive parameters end-to-end.
• Enhanced scalability for extremely large datasets via hierarchical or approximate attention computation.

The method provides a concrete protocol for hybrid modeling, balancing accuracy, personalization, and interpretability in heterogeneous tabular systems.

Conclusion

"Supervised learning pays attention" (2512.09912) delivers a technically rigorous, broadly applicable, and interpretable framework for attention-weighted supervised modeling in tabular data. By operationalizing supervised similarity and local adaptation, the method consistently improves performance and exposes latent heterogeneity, all while maintaining tractable interpretability. These results suggest meaningful advances in the deployment of flexible, context-aware models for practical prediction, diagnostics, and model correction tasks in statistical machine learning.