F2: Offline Reinforcement Learning for Hamiltonian Simulation via Free-Fermionic Subroutine Compilation (2512.08023v2)

Abstract: Compiling shallow and accurate quantum circuits for Hamiltonian simulation remains challenging due to hardware constraints and the combinatorial complexity of minimizing gate count and circuit depth. Existing optimization method pipelines rely on hand-engineered classical heuristics, which cannot learn input-dependent structure and therefore miss substantial opportunities for circuit reduction. We introduce F2, an offline reinforcement learning framework that exploits free-fermionic structure to efficiently compile Trotter-based Hamiltonian simulation circuits. F2 provides (i) a reinforcement-learning environment over classically simulatable free-fermionic subroutines, (ii) architectural and objective-level inductive biases that stabilize long-horizon value learning, and (iii) a reversible synthetic-trajectory generation mechanism that consistently yields abundant, guaranteed-successful offline data. Across benchmarks spanning lattice models, protein fragments, and crystalline materials (12-222 qubits), F2 reduces gate count by 47% and depth by 38% on average relative to strong baselines (Qiskit, Cirq/OpenFermion) while maintaining average errors of 10^-7. These results show that aligning deep reinforcement learning with the algebraic structure of quantum dynamics enables substantial improvements in circuit synthesis, suggesting a promising direction for scalable, learning-based quantum compilation

• The paper introduces F2, merging offline RL with free-fermionic subroutine compilation to significantly reduce gate counts and circuit depths in Trotter simulations.
• It leverages a dual-tower neural architecture with compositional embeddings to efficiently navigate the complex, structured action space inherent in quantum circuit synthesis.
• Empirical benchmarks show up to 80% resource savings with fidelity errors below 10⁻⁷, making F2 a promising approach for scalable, NISQ-era quantum applications.

Offline Reinforcement Learning for Quantum Hamiltonian Simulation: F2 and Free-Fermionic Subroutine Compilation

Introduction and Motivation

Quantum simulation, particularly of many-body Hamiltonian dynamics, faces dual scaling challenges: the exponential growth in Hilbert space precludes classical simulation for all but the smallest systems, while the resource limitations of near-term quantum hardware—limited qubit counts, low gate fidelities, and restricted connectivity—severely constrain feasible quantum circuit depths and gate counts. Traditional quantum compilers based on hand-engineered, static heuristics (Qiskit, Cirq, OpenFermion) provide only modest circuit reductions due to their inability to exploit input-dependent algebraic structure in complex Hamiltonians, especially for Trotterized time-evolution.

The F2 framework proposes a fundamentally different approach: hybridizing learning-based optimization with algebraic exploitation of classically tractable subroutines, specifically free-fermionic Hamiltonian fragments. By imposing structure-aware reinforcement learning within offline-generated, guaranteed-successful trajectories, F2 achieves significant compression of Trotter simulation circuits, yielding strong reductions in gate count and circuit depth while targeting user-prescribed fidelity thresholds.

RL Environment Design for Structured Quantum Compilation

The central insight is that large classes of physically-relevant Hamiltonians feature extensive subdomains that are free fermionic (i.e., quadratic in creation/annihilation operators), and are thus classically simulatable (scaling as $O(n^2)$ for $n$ orbitals) and efficiently mappable to quantum circuits via standard transformations (e.g., Jordan–Wigner). F2 modularizes the decomposition of each Trotter step into two streams: exponential unitaries for non-classically-tractable fragments, and classically simulatable subcircuits suitable for aggressive RL-based optimization (Figure 1). The RL agent is tasked with exactly synthesizing the target free-fermionic unitary (or achieving sub-$\epsilon$ distance per fidelity constraints) through sequential composition of parameterized Pauli-string exponentials, corresponding to analytically decomposed operations.

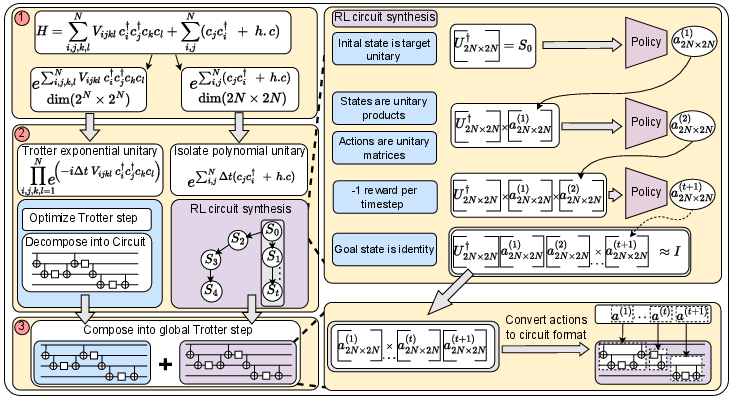
Figure 1: Workflow of F2—separating Hamiltonian terms, compiling non-tractable and free-fermionic fragments, constructing the RL trajectory, mapping actions to circuits, and concatenating into an optimized Trotter step.

The RL state is formalized as the current residual unitary (product of target with the realized circuit thus far), the action space comprises exponentials of 1–2 qubit Pauli strings with discrete rotation parameters, and rewards are strictly length-minimizing (negative step count) given the efficiency needs of hardware. Actions have deterministic dynamics in the restricted subspace and map unambiguously to quantum circuits.

F2 Policy Architecture: Dual Representation and Compositional Embedding

Learning efficiency in this RL setting is constrained by two technical challenges: the exponential and highly structured action space and the long-horizon credit assignment. To address these, F2 employs a dual-tower neural architecture: one tower encodes the current unitary matrix using axial attention to capture algebraic correlations, while the other tower encodes the action sequence using a custom compositional embedding. Rather than one-hot encoding actions, this embedding factors along dimensions such as Pauli operator types, rotation angles, Pauli string length, and global position, allowing token proximity in embedding space to reflect intrinsic operator similarity (Figure 2).

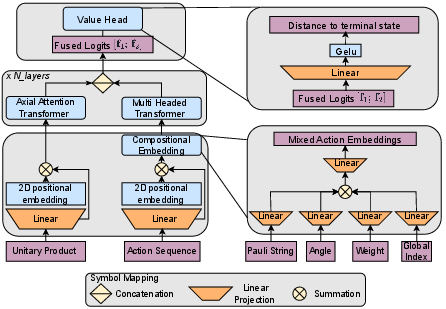
Figure 2: The dual-tower policy—matrix tower (axial attention) consumes the unitary state, while the sequence tower processes finely-grained compositional embeddings, facilitating efficient generalization over the hybrid action space.

Ablation of the compositional embedding (replacement with na\"ive one-hot) substantially degrades label learning efficiency, especially as action space and system size grow. Quantitatively, the compositional baseline converges faster and to lower loss, affirming the benefit of factorized action representations (Figure 3).

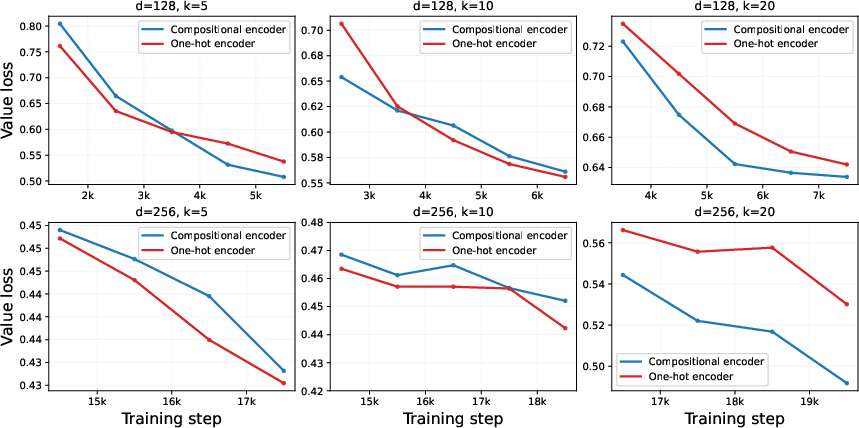
Figure 3: Loss comparison of action embedding architectures demonstrates superior and scalable label efficiency for the compositional representation, accelerating convergence especially as the action space size increases.

Synthetic Trajectory Generation via Quantum Reversibility

Sparse rewards are problematic in quantum circuit compilation. F2 circumvents this by synthesizing dense offline datasets through trajectory reversal: Due to the invertibility of unitary evolution, successful RL trajectories can be generated by stochastically sampling action sequences backward from the identity operator. Each reversed frame is labeled by its distance-to-goal (steps remaining), supporting efficient regression even for long-horizon tasks. Unlike standard time-symmetry or HER-based augmentation, this approach guarantees on-goal coverage without relabeling, sidestepping reward sparsity endemic to quantum RL.

Geometric Regularization of the Value Function

Standard Monte-Carlo regression over step counts is agnostic to the geometric properties of the quantum state space. F2 introduces a geometric regularizer into value learning, leveraging the block-diagonal form of free-fermionic unitaries—whose rotation angles sum to zero in the identity case. The regularizer penalizes the sum-of-squares of the canonical block rotation angles, yielding a value function shape positively correlated with geometric proximity to the goal (identity state). This regularizer, with learnable scaling parameters, further stabilizes learning and improves low-error synthesis rates, outperforming potential-based reward shaping, which fails in the offline, guaranteed-success regime where rewards are non-discounted and can be highly anti-correlated with geometric closeness (Figure 4).

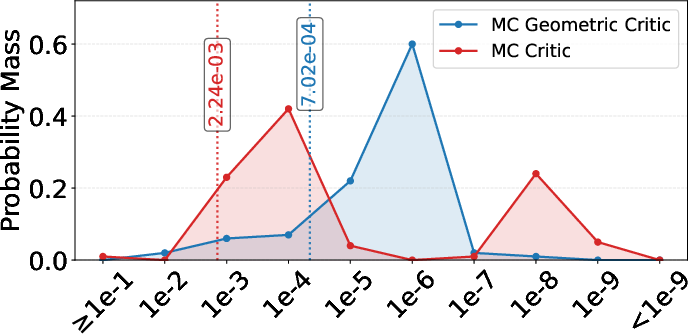
Figure 4: Fidelity error distributions of models trained with geometric regularization show an order-of-magnitude reduction in approximation error over canonical reward shaping, validating the efficacy of learned geometry-aware objectives.

Empirical Results and Benchmarks

F2 is benchmarked on an extensive suite spanning quantum materials models (Fermi–Hubbard, Heisenberg, $t$–$J$), strongly correlated compounds (La$_2$CuO$_4$, $\kappa$-(ET)$_2$Cu$_2$(CN)$_3$), and protein fragments (PD-1, ABL1), across $12$–$222$ qubits and various connectivity/topology classes. Relative to Cirq/OpenFermion and Qiskit, F2 achieves mean reductions of 47% gate count and 38% depth (with maxima above 80% in some instances), all while achieving mean fidelity errors below $10^{-7}$ (Figure 5).

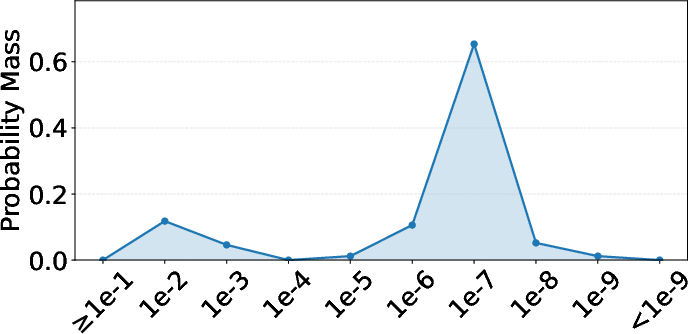
Figure 5: Fidelity accuracy histogram over 500 randomly-sampled unitaries illustrates that the vast majority of compiled circuits achieve error well below $10^{-6}$, affirming tight fidelity control during optimization.

Further analysis clarifies that depth reduction, while positive, is typically less than gate count due to (i) post-compilation commutation/merging passes and (ii) discrete angle decomposition sometimes inflating intermediate circuit widths. Importantly, the flexible approximation threshold enables trading negligible fidelity loss for large-scale resource savings—a critical lever for NISQ and near-term applications.

Related Work and Positioning

The F2 approach departs substantially from prevailing quantum compiler methodology. Existing compiler stacks focus on explicitly-commuting term grouping, block-wise diagonalization, or heuristic Pauli-based gate cancellation [deBrugiere_2024_ShorterSynthesis, li2021paulihedralgeneralizedblockwisecompiler], but do not integrate AI for structured, subspace-specific optimization, nor do they leverage domain-theoretic properties (e.g., Lie algebra closure for free fermions) in RL environments. Prior RL-based attempts at quantum synthesis have been limited to either single- or few-qubit primitives [Zhang2020TopologicalQuantumCompiling, Kolle2024RLQCS, Rietsch_2024], or have omitted algebraic substructure and relied on purely online interaction. F2 demonstrates that inductive bias—both architectural and domain-theoretic—combined with synthetic, dense data, dramatically improves both convergence and sample-efficiency, scaling learning-based approaches to relevant many-qubit regimes.

Implications and Future Directions

F2 establishes a roadmap for unifying learning-based and algebraic quantum compilation, demonstrating that the strategic identification and RL-driven optimization of classically simulatable subroutines within Trotterization can yield non-trivial resource reductions. These advances suggest further opportunities:

• Integration of tensor network simulation kernels: Extending RL environments to incorporate tensor network–tractable Hamiltonian fragments (e.g., MPS-representable blocks [Orus2014]) could broaden the scope of classically-intractable but scalable subroutine optimization.
• Continuous parameter space actions: Current action spaces are discretized; differentiable policy optimization or implicit continuous action representations could improve compilation efficiency for irregular Hamiltonian coefficient distributions.
• Architectural co-design: Jointly learning compilation strategies cognizant of target hardware (e.g., connectivity, native gate set, error rates) could further enhance hardware-specific circuit efficiency.

More broadly, F2’s data and environment design contribute a template for other quantum compilation tasks, including error correction subroutines and Pauli-based computation architectures.

Conclusion

F2 represents a principled advance in quantum circuit compilation methodology, coupling offline RL with free-fermionic Hamiltonian structure for deep optimization of Trotter steps. By demonstrating robust, architecture- and environment-aware value learning, synthetic trajectory augmentation, and strong empirical performance across materials and biomolecular workloads, F2 sets a precedent for scalable, learning-based quantum program synthesis (2512.08023). The approach constrains circuit overhead in settings where conventional compilers plateau, and provides explicit mechanisms for fidelity control and resource budget targeting. F2's modularity makes it an attractive foundation for future AI-based compilers as quantum hardware matures and system sizes escalate.