Information-Theoretic Analysis of Weak Measurements and Their Reversal (2512.08015v1)

Abstract: We study trade-off relations in information extraction from quantum systems subject to null-result weak measurements, where the absence of a detected photon continuously updates the system state. We present a detailed analysis of qubit and qutrit systems and investigate a general framework for a multilevel quantum system. We develop a dynamical characterization of null-result weak measurements that quantifies the information extracted over time, revealing the amount of the obtained information and also the rate of the information accumulation. The characterizations are obtained by examining the time-dependent evolution of the information theoretic quantities. More specifically, we consider Shannon entropy, mutual information, fidelity, and relative entropy to characterize the weak measurement dynamics. Our results provide an information theoretic analysis of the weak measurement process and highlight the dynamical nature of information extraction and reversibility in the weak measurement processes.

• The paper demonstrates how null-result weak measurements extract information while simultaneously causing coherence loss, quantified by Shannon entropy and fidelity metrics.
• It applies a time-dependent framework on qubit and qutrit systems, showing that measurement dynamics critically depend on the initial prior distribution.
• The findings inform quantum error correction and adaptive control by linking measurement disturbance with instantaneous rates of state reversibility and decoherence.

Information-Theoretic Characterization of Null-Result Weak Measurements and Reversibility

Introduction

This work addresses the dynamics of information extraction and reversibility in quantum measurements performed via null-result (no-click) weak monitoring, extending analysis to both qubits and qutrits and generalizing to multilevel quantum systems. Weak measurements, distinguished from projective measurements by their non-destructive nature, allow continuous information acquisition without immediate wavefunction collapse. The investigation is situated within an information-theoretic framework, focusing on time-dependent quantities—Shannon entropy, mutual information, fidelity, and relative entropy—to precisely quantify both the information gained and the corresponding loss or recovery of coherence. The analysis links these quantities to reversibility, decoherence, and irreversibility, thereby providing new insights pertinent for quantum error correction, feedback, and open systems control.

Null-Result Weak Measurement Framework

The system resides in a Fock-state superposition, $\ket{\psi} = \sum_{n=0}^{N} c_n \ket{n}$, undergoing continuous, photon-detection-based monitoring. Absence of detection events for a time $t$ constitutes a null result, implemented via the non-unitary operator $M_0 = e^{-\gamma t \hat{n}}$, with cavity decay rate $\gamma$. The ensuing conditional state has coefficients $c_n e^{-n\gamma t}$, and the null result probability is $p(y_0) = \sum_{n=0}^{N} |c_n|^2 e^{-2 n \gamma t}$. Bayesian updating yields the posterior photon number distribution:

$$p(x_n| y_0) = \frac{|c_n|^2 e^{-2 n \gamma t}}{\sum_{m=0}^{N} |c_m|^2 e^{-2 m \gamma t}},$$

enabling classical treatment of information-theoretic measures over quantum trajectories.

Dynamical Information-Theoretic Quantifiers

The central quantities analyzed include:

• Shannon Entropy: Quantifies prior and posterior uncertainty, with information gain $I(0) = H(X) - H(X|y_0)$.
• Mutual Information: Ensemble average over measurement outcomes.
• Classical Fidelity: Overlap between prior and post-selected distributions, reporting disturbance magnitude.
• Relative Entropy: Asymmetric measure of distinguishability (Kullback-Leibler divergence) between prior and posterior.
• Reversal Probability: Conditional recovery chance for pre-measurement state, operationally relevant for quantum error recovery.

The dynamics of these quantifiers, as illustrated for qubit and qutrit systems, underscore the influence of the prior distribution on information gain and reversibility.

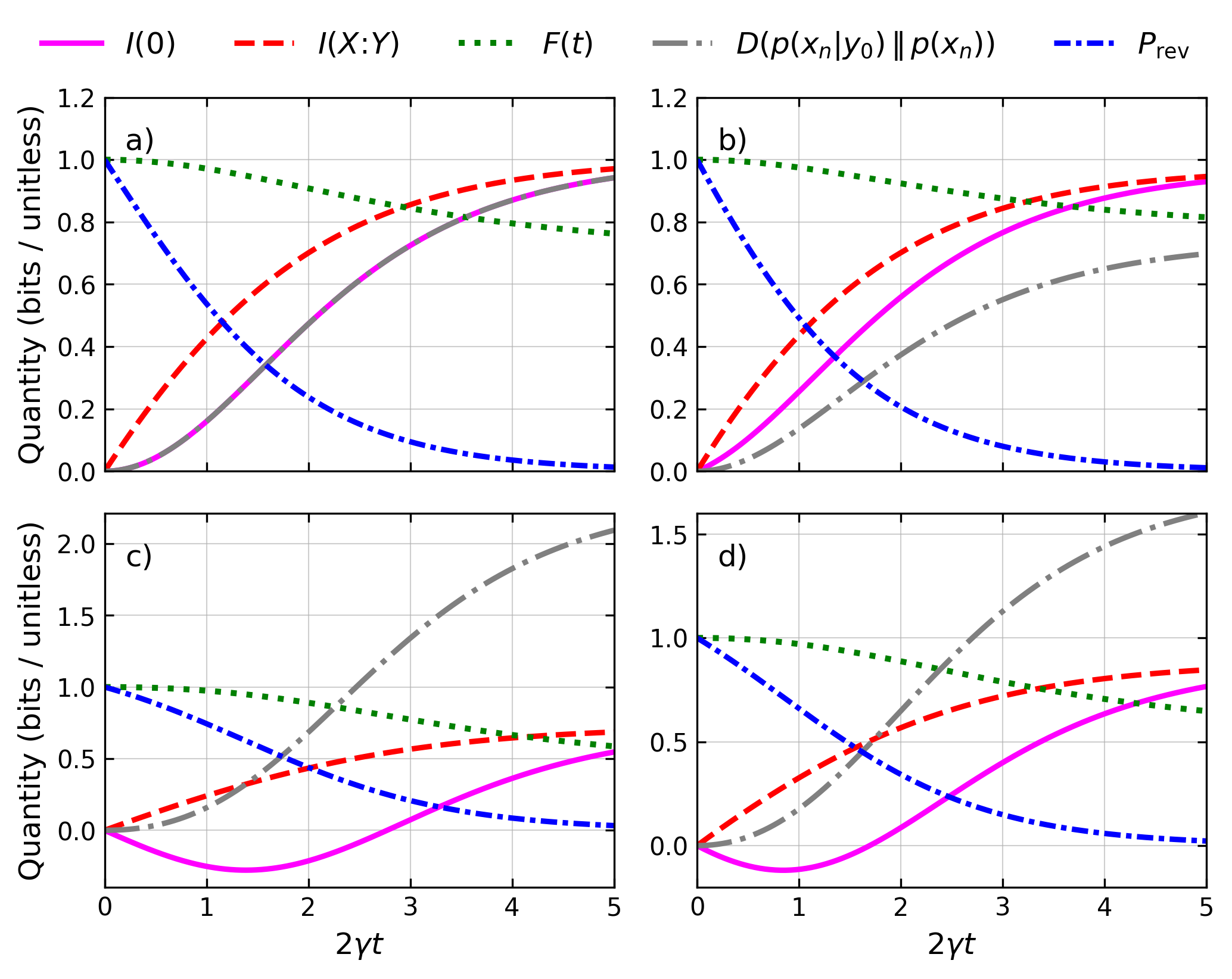
Figure 1: Information-theoretic measures (information gain, mutual information, fidelity, reversal probability, and relative entropy) for qubit null-result monitoring and four representative priors $p(x_n)$.

For qubits, information gain, mutual information, and relative entropy converge asymptotically, reflecting that all accessible information is extracted by long-time null monitoring. For nonuniform priors, the relative entropy increases more rapidly and to higher values, indicating intensified state distinguishability and irreversibility.

Figure 2: Information-theoretic measures under null-result qutrit monitoring for various priors, extending the qubit analysis to higher dimensions.

For qutrits, coherence is lost and reversibility is compromised more quickly than for qubits, as evidenced by the sharper drop in fidelity and reversal probability. Both the speed and the saturation levels of all quantifiers are strongly prior-dependent.

A noteworthy result is the emergence of negative instantaneous information gain for selected prior/posterior pairs at short times—not commonly highlighted in previous studies. This reflects cases where the null-result measurement, by updating the prior toward lower photon numbers, may transiently increase uncertainty with respect to the optimal estimator.

Rates of Information Extraction and Decoherence

The paper extends analysis to the instantaneous rates of change for information gain, fidelity, and reversal probability, enabling a differential view of measurement-induced irreversibility.

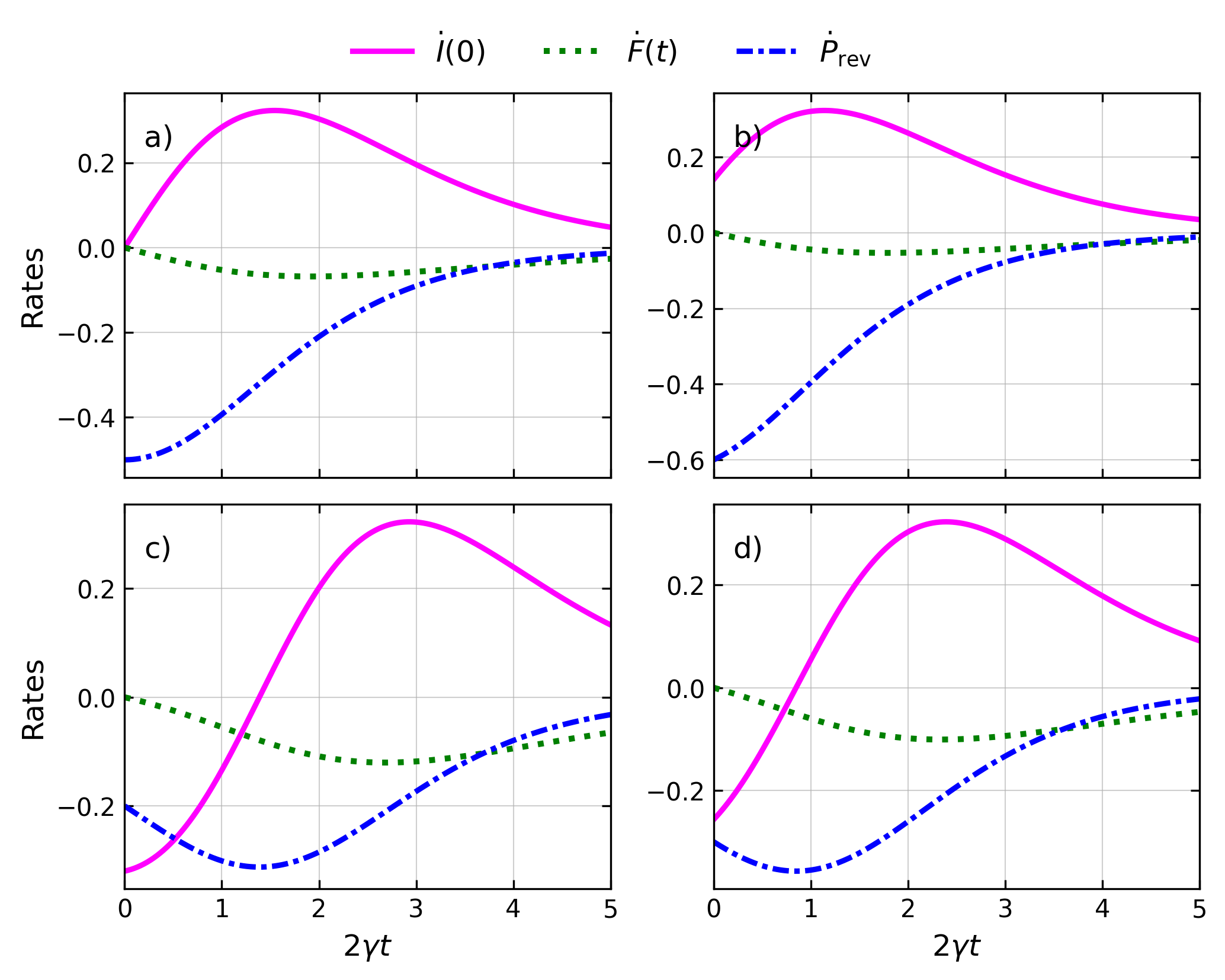
Figure 3: Instantaneous rates of information gain $\dot{I}(0,\tau)$, fidelity decay $\dot{F}(\tau)$, and reversal probability decrease $\dot{P}_\mathrm{rev}(\tau)$ for a qubit under null-result weak measurement.

Key findings include:

• For uniformly mixed priors, initial extraction rates are zero or positive, while certain biased priors yield initial negative rates.
• Fidelity and reversal probability rates are always negative, their minima co-located with the maximum rate of information extraction.
• All rates asymptotically vanish as the system approaches the stationary (projected, mostly vacuum) state.

Threshold analysis (as reported in supporting tables) shows that in qubits, fidelity drops below 90% for $2\gamma t^* \sim 1.9$–$2.1$, while the corresponding threshold for qutrits is $2\gamma t^* \sim 1.0$–$1.25$. Reversal probability falls below 50% on comparable or shorter timescales, particularly in higher dimensions.

Figure 4: Time derivatives of information gain, fidelity, and reversal probability for the qutrit system, highlighting the enhanced and accelerated irreversibility relative to qubits.

The scaling with system dimension shows a pronounced increase in both the rates and the overall magnitude of irreversibility induced by null-result weak measurement.

Implications and Future Directions

The time-resolved, ensemble-averaged framework presented enables systematic quantification of information-disturbance trade-offs along with the feasibility and timing of measurement reversal protocols. The dependency of all measures on the initial prior distribution elucidates fundamental limits on coherence protection and error recovery in open quantum systems. The approach offers concrete tools for optimizing measurement-based control, adaptive protocols, and decoherence mitigation in quantum technology platforms.

The possibility of negative instantaneous information gain raises new questions regarding optimal estimator strategies and the role of prior selection—an avenue for further theoretical and experimental exploration. The accelerated irreversibility seen in higher-dimensional systems points to practical constraints for multi-level quantum computing and communication architectures, motivating the development of more effective weak measurement control and error correction techniques.

Conclusion

This analysis delivers a rigorous, information-theoretic treatment of null-result weak measurement processes, tracking both integral and instantaneous measures of information gain, state fidelity, relative entropy, and reversibility. The results establish a direct connection between measurement-induced information extraction and loss of coherence, expose the dependence on system dimension and prior ensemble statistics, and supply relevant metrics for reversing quantum operations. These findings will inform both foundational quantum measurement theory and the design of resilient protocols in quantum control and error correction (2512.08015).