Emergent Strings from Quantum Field Theory (2512.07928v1)
Abstract: We develop a procedure that reorganizes the perturbative expansion in a class of quantum field theories into a stringy amplitude expressed as a sum over two-dimensional geometries. Using Schwinger parametrization and the one-to-one correspondence between metric ribboned graphs and the moduli space of Riemann surfaces established via Strebel differentials, we map each Feynman diagram to a surface. We then construct a conformal field theory on the worldsheet whose correlation functions encode the full set of QFT Feynman rules directly from the geometry of the associated Riemann surface. Restoring diffeomorphism and Weyl invariance promotes the integral over moduli space to a path integral over worldsheet metrics, yielding a non-critical string theory whose Liouville mode naturally becomes a holographic direction. By construction, the expansion of the string theory amplitudes in the number of boundary state insertions matches the loop expansion in the QFT at fixed genus. Moreover, loop divergences are shown to match standard string-theoretic degeneration limits, indicating that gravitational backreaction is equivalent to QFT renormalization. Our construction provides a microscopic route from generic QFTs to emergent string theories and offers a framework for deriving holographic duals directly from field-theoretic data.
Sponsor
Summary
- The paper presents a formalism that maps QFT Feynman diagrams to worldsheet string amplitudes using Strebel differentials.
- It employs Schwinger parametrization and moduli space integration to reorganize QFT loop expansions into a geometric series corresponding to Riemann surfaces.
- The framework identifies gravitational backreaction with renormalization, setting the stage for constructing holographic duals from generic QFTs.
Emergent String Theory from Perturbative Quantum Field Theory
Background and Motivation
The persistent challenge in theoretical physics has been to derive string theory as a natural emergent structure from the Feynman diagrammatic expansion of quantum field theories (QFTs), especially outside special limits such as large- gauge theories. The conventional approach, initiated by 't Hooft, relies on identifying the genus expansion of ribbon graphs with the topological perturbative expansion of string theories. However, a fully general and constructive framework for this emergence—particularly one that transitions from arbitrary QFTs to string theory amplitudes formulated as worldsheet path integrals—has remained elusive.
This work provides a systematic formalism that recasts QFT amplitudes as a sum over two-dimensional geometries. The approach leverages the Schwinger parametrization of Feynman diagrams and exploits the mathematical correspondence between metric ribbon graphs and the moduli space of Riemann surfaces through Strebel differentials. Each Feynman diagram is mapped to a surface, enabling the construction of a conformal field theory (CFT) whose worldsheet correlation functions encode the QFT's Feynman rules.
Strebel Differentials and Ribbon Graphs to Moduli Space
The central mathematical device in the mapping is the use of Strebel differentials, which provide a bijection between metric ribbon graphs and points in the moduli space of Riemann surfaces with genus and marked points, together with positive residues. The construction involves gluing strips along the edges and vertices of the ribbon graph: horocyclic coordinates are introduced, and each graph topology defines a unique holomorphic atlas on the surface. The Strebel differential encodes both the metric and combinatorial data of the graph.
Figure 1: Construction of a Riemann surface via gluing of strips corresponding to edges and vertices of a ribbon graph. The process establishes a one-to-one correspondence between graphs and Riemann surfaces with marked points.
The volume form on moduli space is naturally induced by the wedge product of the edge-length differentials, which coincides with Kontsevich's cell decomposition and the Weil–Petersson symplectic structure in the appropriate limit. Integration over moduli space thus reorganizes the sum over graph topologies and Schwinger parameters into a geometric integral, crucial for recasting Feynman diagram expansions as worldsheet path integrals.
Amplitudes as Sums over Geometries
Transitioning from individual graphs to sums over all diagrams, the procedure utilizes Schwinger parametrization to encode all propagator multiplicities and edge lengths. Graphs with loops of insufficient length (1 or 2) are resolved by merging propagators, and the measure on moduli space assigns vanishing weight to graphs with long loops. The construction accommodates graphs with arbitrary topology and disconnected components by analytic continuation in the multiplicities. The result is a unified expression:
enabling a geometric interpretation of the perturbative QFT sum.
Figure 2: Splitting higher-length loops into minimal components in both the graph and moduli space, resolving combinatorial ambiguities in topological degenerations.
Worldsheet Path Integral and Gauge Symmetry Restoration
Having mapped QFT diagrams to Riemann surfaces, the next step is to reinterpret the integration over moduli space as a path integral over worldsheet metrics. This requires restoring diffeomorphism and Weyl invariance, and introducing appropriate ghost and Liouville degrees of freedom to compensate for gauge fixing and anomalies. The Liouville mode becomes a dynamical field, inheriting the role of the holographic extra dimension.
The full partition function includes contributions from non-compact target space bosons (encoding QFT variables), large- matrix models, and ultralocal auxiliary fields (to match combinatorial weighting and multiplicity powers), as well as ghost and dilaton sectors encoding moduli measure and anomaly cancellation. The path integral structure is engineered so that summing worldsheet boundary insertions corresponds precisely to the loop expansion at fixed genus in the QFT.
Explicit Construction of the Worldsheet CFT and Feynman Rule Encoding
The geometrization is completed by constructing a worldsheet CFT whose correlation functions replicate the QFT's Feynman rules. The non-compact free boson sector with Dirichlet boundary conditions encodes the spacetime embedding and propagator exponentials, while matrix model fields and additional ultralocal bosonic and fermionic fields realize the precise monomial dependence on propagator lengths and combinatorics.
This CFT is constructed so that, for each surface and insertion pattern, the correlator matches the sum over all Feynman diagrams of matching topology—including correct coupling factors, symmetry factors, and external source handling. The approach permits explicit resummation at fixed genus and boundary number, integrating over the worldsheet moduli and auxiliary fields.
Divergences, Renormalization, and Gravitational Backreaction
A critical analysis is given to the manifestation of loop divergences. The standard UV and IR singularities in QFT map directly onto degeneration loci in moduli space, where worldsheet surfaces develop singular necks or propagators become infinitely long. The equivalence is posited between the need for counterterms (QFT renormalization) and the necessity for including gravitational backreaction in the string (worldsheet) theory.
This identification implies that fully consistent backgrounds—with gravitational backreaction summed to all orders—are required for the emergent string theory to reproduce the QFT without divergence. The work leaves the explicit resolution and computation of backreacted backgrounds as an open direction, but establishes that the Liouville mode naturally serves as the emergent holographic direction, consistent with known conjectures in AdS/CFT correspondence.
Implications and Extensions
The construction provides an explicit microscopic mechanism for realizing string theory amplitudes directly from generic QFTs. It avoids reliance on lattice or phenomenological input and formalizes the emergence of holographic directions in settings beyond traditional AdS/CFT. The framework suggests that the loop expansion of the QFT is encoded in the worldsheet genus expansion and that the dynamics of the emergent holographic dimension (Liouville theory) organize the continuum limit and admit physical interpretation akin to bulk gravity.
Key implications:
- Provides a constructive, universal route from field-theoretic data to string-theoretic amplitudes,
- Enables principled derivation of holographic duals, potentially extending beyond integrable or supersymmetric settings,
- Identifies gravitational backreaction with renormalization, opening avenues for non-perturbative studies of background formation,
- Sets a program for precision holography applicable to real-world QFTs, including potentially QCD and the Standard Model.
Potential future directions include generalizations to derivative interactions, gauge fields, fermions, and the exploration of stringy duals for non-relativistic or Carrollian theories, with the ultimate goal of systematically constructing holographic duals for experimentally relevant theories.
Conclusion
This work establishes an explicit and generalizable formalism mapping perturbative QFT expansions to worldsheet string theories, via Strebel differentials and moduli space geometry. The construction realizes the QFT amplitudes as worldsheet CFT correlation functions, with the genus expansion matching the loop order and the emergent Liouville mode dynamically encoding the holographic dimension. The correspondence between QFT renormalization and gravitational backreaction is made precise at the amplitude level. The implications for holography, background formation, and the foundational structure of string emergence are profound, setting the stage for future work in principle-based derivations of dualities and new precision tools in theoretical and mathematical physics.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
Overview: What this paper is about
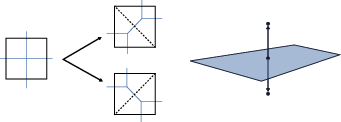
This paper shows a concrete way to turn ordinary quantum field theory (QFT) — the standard framework we use to describe particles and their interactions — into a kind of string theory. The idea is to take each Feynman diagram (those network-like pictures used to calculate particle processes) and convert it into a two-dimensional surface. Then, the authors put a simple set of rules (a “worldsheet” theory) on that surface so that, when you add up all possible surfaces, you exactly reproduce the original QFT answers. In short: they build a bridge from particles to strings directly from the math of Feynman diagrams.
Goals: What the authors wanted to figure out
- Find a general, step-by-step method to map every QFT Feynman diagram to a two-dimensional surface.
- Build a “worldsheet” theory (a conformal field theory, or CFT) that lives on those surfaces and automatically encodes the QFT’s rules for propagators (the lines) and vertices (the interaction points).
- Re-express the usual sum over Feynman diagrams as a sum over the shapes of surfaces (known as moduli space), and then as a path integral over all possible surface geometries (like in string theory).
- Show that problems in QFT (like loop divergences) show up in the string picture in a standard way (as degeneration of surfaces) and can be handled by including gravity’s backreaction — connecting renormalization in QFT to gravity effects in the string picture.
- Provide a practical framework for deriving holographic duals (gravity/string descriptions) directly from field theory data.
Methods: How they built the bridge from diagrams to surfaces
Think of a Feynman diagram as a network of sticks (edges) meeting at joints (vertices). The authors do three key things:
- Give each stick a length using Schwinger parameters
- A standard trick (Schwinger parametrization) rewrites a propagator (a line in the diagram) as an integral over a positive “length.”
- Now every edge in the diagram has a length you integrate over.
- Turn the network into a surface using a mathematical gluing recipe
- They treat the diagram as a “ribbon graph” (edges have a little width and an orientation).
- A tool called a Strebel differential tells you exactly how to glue thin strips together along edges to make a smooth two-dimensional surface with marked points (one for each vertex).
- Different diagram shapes fill out the space of possible surface shapes (this is called a cell decomposition of moduli space).
- Replace “sum over diagrams” with “sum over surfaces,” then restore full geometry
- Once diagrams are surfaces, the calculation becomes an integral over the shapes of surfaces (moduli).
- The authors then “restore the gauge symmetries” (diffeomorphisms and Weyl rescalings) to promote this into a path integral over all possible surface metrics — exactly the string theory setup.
- In doing so, you must include standard stringy ingredients:
- Ghost fields (bookkeeping fields that come from fixing gauge symmetries).
- A Liouville field (captures how the surface can be stretched or squished; it becomes an extra “holographic” direction).
To make the worldsheet CFT reproduce QFT rules:
- They use free bosons with specific boundary conditions to encode the particle positions and propagators.
- They introduce large-N matrix fields and simple auxiliary fields to correctly count how many lines meet at each vertex and to generate the exact dependence on the edge lengths. This takes care of factors like powers of the Schwinger parameters and symmetry factors from identical lines.
- They also handle special cases (like two-line loops or long loops) by cleverly combining multiple propagators into “effective” ones and allowing edges of zero weight with a compensating factor. This ensures every QFT diagram is accounted for without overcounting.
A helpful analogy:
- Imagine building surfaces out of paper strips: each Feynman line is a strip with a length. You glue strips around loops and joints using a rulebook so the whole thing makes a smooth surface. Then, you paint simple patterns on the surface (the worldsheet theory). When you add up all possible shapes and patterns, you get the same number you would have gotten by adding up all Feynman diagrams.
Main findings: What they discovered and why it matters
- A full reorganization of QFT into string-like amplitudes: The authors show how to rewrite a wide class of QFT calculations as sums over two-dimensional surfaces with a worldsheet CFT. This is not just a metaphor — it’s a detailed, step-by-step map.
- A concrete worldsheet theory that encodes QFT Feynman rules: By choosing the right fields and boundary operators on the surface, the correlation functions reproduce the QFT propagators, vertex factors, and symmetry factors automatically.
- The Liouville mode acts like a holographic direction: When you restore Weyl symmetry (rescaling the surface), a new scalar field (the Liouville field) appears. It naturally plays the role of an extra dimension, aligning with the idea of holography (where a lower-dimensional system encodes a higher-dimensional one).
- Loop counting matches on both sides: The expansion of string amplitudes in the number of boundary insertions mirrors the loop expansion in QFT at fixed genus (genus counts “handles” on the surface, like donut holes). So string “topology expansion” and QFT “loop expansion” line up.
- Divergences match standard string degeneration limits: The infinities in QFT loop diagrams show up as surfaces pinching or tearing in the string picture — the usual way strings develop divergences. Fixing them corresponds to including gravitational backreaction, which mirrors renormalization in QFT. This reveals a deep link: QFT renormalization ≈ gravity adjusting the background.
Implications: Why this approach could matter in the long run
- A microscopic route to holography: Instead of guessing what the gravity dual of a QFT might be, this method builds a string description directly from the QFT’s Feynman diagrams. That’s a big step toward a general understanding of when and how holography works.
- New computational tools: If refined, this could let physicists compute tough QFT quantities by switching to surface sums, potentially opening new precision methods (especially near regimes where string methods are powerful).
- Conceptual clarity: It suggests that the “emergence” of extra dimensions and gravity from QFT is tied to how we reorganize the QFT’s internal bookkeeping — with the Liouville mode providing the holographic direction and renormalization corresponding to gravitational backreaction.
- Next steps: The current construction focuses on a broad but specific class of QFTs (e.g., massless scalars with simple interactions) and does not yet include full gravitational backreaction or specific AdS backgrounds. Extending to more general fields (like gauge fields and fermions), fully incorporating backreaction, and exploring concrete holographic spacetimes are natural future directions.
In simple terms: this paper turns the puzzle of “How do strings emerge from particles?” into a concrete recipe. It shows that by carefully re-labeling and gluing the pieces of QFT calculations, a string world — complete with its own geometry and extra holographic direction — naturally appears.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a single, concrete list of what remains missing, uncertain, or unexplored in the paper—framed to be actionable for future research.
- Generality of the construction: The paper focuses on QFTs with massless scalar propagators and momentum-independent vertices; a roadmap is needed to extend the procedure to:
- Massive fields (including how masses modify the Schwinger-parametric map and the worldsheet exponentials).
- Derivative and momentum-dependent interactions (how to encode momentum flow and tensor structures on the worldsheet).
- Fermions and gauge fields (including spin, gauge redundancy, and color factors), as well as supersymmetric theories.
- Finite-N (non-planar) corrections and theories without large-N expansions.
- Combinatorial completeness and double counting: The use of multiplicity-0 “edges” and a factor of 1/2 to reconstruct graphs with loops of length ≥4 is heuristic. A rigorous combinatorial proof is needed that:
- All target diagrams are generated exactly once across moduli cells.
- Symmetry factors, automorphisms, and edge-homotopy constraints are handled correctly.
- Tadpoles, self-edges, and non-homotopic multiple edges between the same pair of vertices are consistently treated.
- Measure equivalence and determinants: The mapping from the Schwinger measure to the Kontsevich/Weil–Petersson measure is argued via asymptotic limits. It remains to:
- Derive the equality of measures (including the determinant term) rigorously for surfaces with conical singularities and boundaries.
- Clarify the handling of zero modes under Dirichlet/Neumann boundary conditions and confirm independence from the regulator L and choice of reference metric.
- Determine the precise role of corner/cusp contributions in determinant calculations.
- Worldsheet CFT consistency: The proposed CFT (free bosons + large-N matrix model + bilocal auxiliary fields + ghosts + Liouville) is non-standard. It is unclear whether it defines a consistent 2D CFT:
- Prove modular invariance, locality (or precisely define and justify nonlocality), and unitarity/reflection positivity.
- Establish a well-defined operator algebra and OPEs, including at conical singularities (marked points) and with bilocal insertions.
- Provide a BRST formulation and show closure with the ghost/Liouville sectors.
- Central charge accounting and anomaly cancellation: The total central charge appears ill-defined due to large-N matter. A concrete calculation is needed to:
- Quantify contributions from d free bosons, matrix matter, bilocal fields, bc ghosts (c = −26), and Liouville.
- Demonstrate exact cancellation of the Weyl anomaly (or specify the non-critical string background that compensates it).
- Clarify how the auxiliary ghost proposed to accompany the matrix model restores c-total = 0.
- Boundary state normalization and residues: The mapping of boundary conditions to residues a_i via the dilaton is sketched but not fully fixed. Open tasks include:
- Providing the exact normalization of boundary states (including the e{πL/(12 a_i)} factors), ensuring the integrated insertions reproduce QFT amplitudes with correct overall constants.
- Demonstrating explicitly how dilaton zero modes and boundary-length constraints implement the moduli-space measure over a_i.
- Regulator and α′-limit: The identification α′ = 1/(πL) (and L → ∞) is central to matching exponents, but its physical meaning is unclear. Questions:
- Is the emergent string obtained only in the α′ → 0 (infinite tension) limit? What physics survives at finite L (finite α′)?
- Do correlation functions and determinants converge uniformly as L → ∞, and what is the precise order of limits (genus sum, boundary insertions, α′ → 0)?
- Matching of QFT divergences to worldsheet degeneration: The claim that loop divergences correspond to standard degeneration limits and that gravitational backreaction equals renormalization needs concrete evidence:
- Provide explicit computations (e.g., 1- and 2-loop examples) showing equality of divergent structures and the mapping of counterterms to backreacted worldsheet/target-space data.
- Clarify scheme dependence: how does QFT renormalization scheme map to choices of worldsheet regularization and background fields?
- Emergent spacetime and holography: The Liouville mode is proposed as a holographic direction, but the emergent target-space is unspecified. Open problems:
- Derive the effective target-space geometry (AdS or otherwise) from the worldsheet beta functions and backreaction.
- Construct a holographic dictionary (operator/state map, correlators, scaling dimensions), demonstrating bulk locality and boundary QFT reconstruction.
- Identify the conditions under which different QFTs yield the same or distinct emergent spacetimes.
- Practical computability without explicit Strebel data: The paper avoids constructing explicit Strebel differentials by restoring gauge symmetries, but the integrand still depends on moduli in a way that encodes graph data:
- Provide an algorithm to compute the integrand at a generic moduli point without reconstructing the critical graph (i.e., fully from worldsheet correlators).
- Show that the auxiliary matrix and bilocal fields automatically select the correct edge structure for any point in moduli space.
- Bilocal auxiliary fields and non-geometric actions: The ultralocal actions for M(z,z′) and s(z,z′) are defined via “probability distributions” rather than standard path integrals. Needed clarifications:
- A mathematical construction of these measures on Σ × Σ/∼ for uncountable sets (e.g., via cylindrical measures or discretization limits) ensuring well-defined correlators.
- How these non-geometric fields respect diffeomorphism/Weyl invariance and modular properties of the worldsheet.
- Whether the approach can be reformulated in a geometric or local manner (e.g., via auxiliary worldsheet fields with standard kinetic terms) without losing functionality.
- Symmetry factors beyond multiplicity: While 1/m! factors for parallel propagators are addressed, broader graph automorphisms and combinatorial weights may arise:
- Develop a general counting algorithm to ensure exact inclusion of all symmetry factors for arbitrary topologies and multiplicities.
- Address potential over-/under-counting in disconnected graphs generated via m = 0 edges.
- Treatment of loops of length 1 and 2: The initial construction excludes these, then reintroduces effects via joining homotopic propagators:
- Formalize the handling of tadpoles and double edges, including cases where propagators are non-homotopic.
- Verify that the Strebel-based measure assigns the correct weight to diagrams after these modifications.
- Determinants on singular surfaces: The replacement P1†P1 → (scalar Laplacian)2 on locally flat metrics with conical points and boundaries needs validation:
- Compute determinant corrections due to conical singularities, boundary geodesics, and finite-length strip regulators.
- Confirm that these corrections do not spoil the Weil–Petersson matching or the final amplitude equivalence.
- Unitarity and reflection positivity: Since the worldsheet theory is nonstandard and bilocal, it is necessary to:
- Prove unitarity (or specify conditions under which unitarity holds) and reflection positivity of the emergent string amplitudes.
- Ensure that Wick rotations between Euclidean and Lorentzian signatures are well-defined for both QFT and worldsheet formulations.
- Explicit resummation at fixed genus: The paper claims the sum over graph order can be performed at fixed genus to yield a worldsheet effective action:
- Provide explicit resummations for low genera (e.g., g = 0, 1) and compare with known QFT amplitudes.
- Identify conditions for convergence and control of the genus expansion.
- Color and ribbon structure in gauge theories: For future extension to gauge theories:
- Show how color indices and ribbon structure are encoded on the worldsheet (beyond Strebel duality), including nonplanar contributions.
- Determine how large-N ’t Hooft coupling affects the moduli-space integrand and the emergent geometry.
- Operator insertion rules and momentum flow: The current construction integrates over positions X_i and uses Dirichlet boundary states:
- Extend to momentum-space rules with proper tracking of momentum conservation and flow through vertices.
- Clarify how derivative interactions (e.g., higher-spin couplings) map to worldsheet operator insertions.
- Examples and benchmarks: The framework would benefit from worked examples:
- Compute specific amplitudes (tree-level and low loops) in a simple interacting scalar theory and show exact matching.
- Validate the method against cases where Gopakumar’s free-theory approach is known, to isolate differences due to interactions and the present resummation.
- Dependence on choice of gauge fixing and coordinates: The construction employs specific gluing maps and gauges (hyperbolic/Strebel limits):
- Analyze sensitivity of results to different gauge-fixing schemes and strip gluing choices, including orientation and numbering conventions.
- Ensure independence of physical amplitudes from these choices.
- Scheme for backreaction and background selection: The paper defers gravitational backreaction and does not obtain an AdS background:
- Develop a procedure to incorporate backreaction self-consistently (e.g., via worldsheet beta functions or effective action minimization).
- Identify the background fields (metric, dilaton, RR fluxes if extended) required to cancel degeneration divergences and yield a consistent spacetime.
- Clarification of the role of residues a_i as moduli versus auxiliary parameters: Residues are both part of moduli and affected by Weyl transformations:
- Provide a precise prescription for fixing/resumming over a_i, including their measure and how they enter the final string amplitude.
- Reconcile the breaking/restoration of gauge invariance with constraints on residues and their integration.
Glossary
- AdS/CFT correspondence: A conjectured duality between gravity in Anti-de Sitter space and conformal field theories. "Many attempts exists to offer a derivation of the AdS/CFT correspondence"
- bi-local field: A field that depends on two points on a manifold simultaneously. "the bi-local bosonic scalar field "
- boundary state: An operator/state in worldsheet CFT that enforces specific boundary conditions. "The boundary state for Dirichlet boundary conditions fixed to around a pole at with residue is"
- boundary state insertions: Insertions of boundary states on the worldsheet that encode boundary conditions or interactions. "the expansion of the string theory amplitudes in the number of boundary state insertions matches the loop expansion in the QFT at fixed genus"
- central charge: A parameter of a CFT that measures its degrees of freedom and appears in anomalies. "we will assume that it can be written as a partition function of some CFT of central charge "
- conformal field theory (CFT): A quantum field theory invariant under conformal (angle-preserving) transformations. "construct a conformal field theory on the worldsheet"
- cotangent line bundle: The line bundle of covectors at a point; here the cotangent space at a marked point on a Riemann surface. "cotangent line bundle of the surface at the marked point "
- degeneration limits: Limits in moduli space where the worldsheet becomes singular or pinches, corresponding to divergent behaviors. "string-theoretic degeneration limits"
- diffeomorphism orbit: The set of metrics or fields related by smooth coordinate transformations. "the path integral over the diffeomorphism orbit of the metric "
- Dirichlet boundary conditions: Boundary conditions fixing the value of a field on the boundary. "the determinant of the Laplacian on the strip with Dirichlet boundary conditions is given by"
- dual graph: A graph obtained by exchanging vertices with faces/loops, encoding complementary combinatorial information. "its dual graph (resulting from changing loops to vertices and vertices to loops with two loops connected if they share an edge)"
- Faddeev–Popov determinant: The determinant factor arising from gauge fixing in path integrals. "For the ghosts, their contribution is well known to be "
- Feynman diagram: A graphical representation of terms in perturbation theory for quantum field processes. "map each Feynman diagram to a surface"
- Feynman rules: Prescriptions assigning mathematical expressions to elements of Feynman diagrams. "encode the full set of QFT Feynman rules"
- gauge/gravity correspondence: The idea that certain gauge theories are dual to gravity theories. "The gauge/gravity correspondence has been tested in many scenarios"
- genus: The number of handles of a surface; a topological invariant classifying Riemann surfaces. "An important point is that renormalizing genus graphs requires counterterms with different genus"
- ghosts: Auxiliary fields introduced by gauge fixing that contribute to the measure and determinants. "the ghosts sector of bosonic string theory"
- holomorphic map: A complex-analytic (conformally differentiable) function between complex manifolds. "by the holomorphic map"
- holographic duals: Gravitational/string-theoretic dual descriptions of quantum field theories. "deriving holographic duals directly from field-theoretic data"
- hyperbolic metric: A metric of constant negative curvature on a surface. "the hyperbolic metric of a generic Riemann surface"
- large-N limit: The limit where the number of colors (matrix size) N goes to infinity, simplifying gauge/matrix models. "particularly in the large- limit"
- Laplace transform: An integral transform that converts a function of a variable (e.g., σ) into a function of a conjugate variable. "readily identified as the Laplace transform of "
- Laplacian: The differential operator ∇² governing diffusion/propagation on a manifold. "the determinant of the Laplacian on the strip with Dirichlet boundary conditions"
- Liouville field: The scalar field that restores Weyl invariance in non-critical string theory/path integrals over metrics. "introduces a Liouville field to compensate any Weyl anomalies"
- Liouville mode: The dynamical degree of freedom associated with the Weyl factor on the worldsheet. "a non-critical string theory whose Liouville mode naturally becomes a holographic direction"
- marked point: A distinguished point on a Riemann surface, often corresponding to insertions or punctures. "there is a marked point for every vertex in the graph"
- matrix model: A field theory of matrix-valued fields, often studied in the large-N limit. "A non-geometric large-N matrix model"
- metric ribboned graph: A graph with a cyclic order at each vertex and assigned edge lengths. "the space of metric ribboned graphs of genus with vertices"
- moduli space: The parameter space of inequivalent geometric structures (e.g., Riemann surfaces with marked points). "the moduli space of Riemann surfaces"
- multiplicity: The number of parallel propagators/edges between two vertices in a diagram. "with being a positive integer which corresponds to the multiplicity"
- Neumann boundary conditions: Boundary conditions fixing the derivative normal to the boundary to vanish. "This is just a free scalar field with Neumann boundary conditions"
- non-compact free boson: A free scalar field taking values in an unbounded target space. "A natural guess for a CFT which can encode these types of factors is the non-compact free boson"
- non-critical string theory: A string theory without the critical dimension/central charge balance, requiring Liouville dynamics. "yielding a non-critical string theory"
- path integral: The functional integral over all field configurations or metrics. "path integral over all metrics"
- QFT renormalization: The process of absorbing divergences into redefinitions of parameters in quantum field theory. "gravitational backreaction is equivalent to QFT renormalization"
- residue: The coefficient related to a pole; here the length associated with a marked point in the Strebel differential. "the residues at the marked points actually parametrize "
- Riemann surface: A one-dimensional complex manifold. "define a Riemann surface"
- Schwinger parametrization: A representation of propagators via integrals over auxiliary parameters (Schwinger parameters). "Schwinger parametrization"
- Strebel differential: A quadratic differential with closed trajectories that encodes ribbon graph data on a Riemann surface. "Strebel differential defined as the quadratic differential"
- Strebel metric: The locally flat metric derived from the absolute value of the Strebel differential. "the Strebel metric itself corresponds to this same limit of the hyperbolic metric"
- Strebel parametrization: The gauge choice/coordinatization of moduli space using Strebel differentials and residues. "The Strebel parametrization of moduli space"
- Weil–Petersson symplectic form: The natural symplectic structure on moduli space of Riemann surfaces. "the corresponding Weil--Petersson symplectic form"
- T-duality: A symmetry relating theories with compactification radii R and 1/R; interchanges Dirichlet and Neumann conditions. "T-duality implies that the dilaton determinant with Neumann boundary conditions will also be the same up to normalization"
- topological expansion: An organization of amplitudes by the topology (genus) of the worldsheet or graph. "a topological expansion similar to perturbative string theory emerges"
- Weil–Petersson metric: The Riemannian metric associated with the Weil–Petersson form on moduli space. "equation \eqref{eq:measure} is precisely the Weil--Petersson metric"
- Weyl anomaly: The breakdown of Weyl (scale) invariance at the quantum level. "the Weyl anomaly of the measure"
- Weyl invariance: Local scale invariance of the metric in two-dimensional gravity/string theory. "Restoring diffeomorphism and Weyl invariance"
- worldsheet: The two-dimensional surface traced by a propagating string. "construct a conformal field theory on the worldsheet"
- zeta function regularization: A method to define infinite products/determinants via spectral zeta functions. "We have used zeta function regularization to compute the infinite product"
Practical Applications
Practical, real‑world applications derived from the paper
Below, we group actionable applications of the paper’s findings and methods under Immediate Applications (deployable with existing techniques and within current scope/assumptions) and Long‑Term Applications (requiring further research, scaling, or generalization beyond the present work). Where useful, we indicate sector relevance, likely tools/products/workflows, and key assumptions/dependencies that influence feasibility.
Immediate Applications
These can be explored now within the paper’s stated scope (massless scalar QFTs with momentum‑independent vertices, large‑N/topological expansion, Schwinger parametrization, and worldsheet CFT constructions), primarily in academia and scientific computing.
- Computational reorganization of perturbation theory via moduli‑space integrals
- Use case: Recast high‑loop perturbative amplitudes in suitable scalar QFTs as integrals over the moduli space of Riemann surfaces using the Strebel differential/ribbon‑graph correspondence, reducing the combinatorial burden of summing diagrams topology by topology.
- Sector: Academia (high‑energy theory, mathematical physics), Software (scientific computing/HPC).
- Tools/workflows:
- Graph2Surface: a library that maps Schwinger‑parametrized ribbon graphs to points/cells in M_{g,n}×R_+n (using Strebel differentials and cell decomposition).
- ModuliSampler: Monte Carlo/numerical integration over moduli space using the Kontsevich/Weil–Petersson–related measure.
- Assumptions/dependencies: Initial restriction to massless scalar QFTs; quality of numerical Strebel differential solvers; control at large‑N; numerical stability for degeneration regions.
- Divergence diagnostics and renormalization guidance from geometry
- Use case: Identify and organize loop divergences by analyzing degeneration limits of the associated Riemann surfaces, aiding renormalization scheme design and cross‑checking counterterms.
- Sector: Academia (QFT, string theory), Software (symbolic/numeric).
- Tools/workflows:
- Degen2Counterterm: a diagnostic that flags degeneration channels corresponding to UV/IR divergences and proposes counterterm structure compatible with the topological expansion.
- Assumptions/dependencies: Precise mapping of divergence channels to worldsheet degenerations; still within perturbation theory; gravitational backreaction equivalence noted but not yet implemented.
- Worldsheet‑based testbeds for reproducing QFT Feynman rules
- Use case: Construct toy worldsheet CFTs (free bosons with Dirichlet boundary states + ghost + Liouville sectors) whose correlators reproduce QFT propagator structure and couplings for chosen scalar models; validate graph‑by‑graph matching at fixed genus.
- Sector: Academia (holography, CFT), Education.
- Tools/workflows:
- WorldsheetCFT‑Builder: assemble boundary state insertions D(X_i; z_i) and compute correlation functions that encode Schwinger‑parameter dependence and symmetry factors.
- Assumptions/dependencies: Matching currently demonstrated for massless scalars with momentum‑independent vertices; non‑critical strings with Liouville; careful normalization and determinant factors.
- Software acceleration for Schwinger‑parameterized amplitudes
- Use case: Automate joining of homotopic propagators, inclusion of multiplicity‑0 edges (for loops ≥4), and symmetry‑factor accounting; streamline symbolic/numeric pipelines for high‑loop amplitudes.
- Sector: Software (scientific computing for HEP/condensed matter), Academia.
- Tools/workflows:
- SchwingerParamSuite: symbolic routines for propagator joining and edge‑multiplicity bookkeeping; interfaces to sector‑decomposition/Monte Carlo integrators.
- Assumptions/dependencies: Correct identification of homotopic edges; completeness of multiplicity‑0 prescriptions.
- Large‑N/matrix‑model inspired combinatorics for diagram selection
- Use case: Use large‑N single‑trace factorization and auxiliary (bi‑local) matrix fields to algorithmically select valid pairings/edges in multi‑edge situations when summing over candidate connections.
- Sector: Academia (QFT/string/matrix models), Software (combinatorial engines).
- Tools/workflows:
- PairingSelector: auxiliary‑field based generators to produce only admissible edge pairings consistent with a given graph topology in the strict large‑N limit.
- Assumptions/dependencies: Formal ultralocal bi‑local field integrals used as generating devices; interpretation is algorithmic rather than physical.
- Pedagogical visualization and curriculum design
- Use case: Visual teaching tools that map Feynman diagrams to surfaces, illustrate Strebel strip gluing, and show how degeneration limits mirror loop divergences; modules on emergent strings from QFT.
- Sector: Education (graduate physics curricula), Software (visualization).
- Tools/workflows:
- Ribbon2Riemann Visualizer: interactive app to glue strips around vertices/loops and display the induced Strebel differential, zeros/poles, and metric features.
- Assumptions/dependencies: Visualization relies on robust numerical routines for quadratic differentials.
- Policy‑adjacent: shared infrastructure for moduli‑space computations
- Use case: Community repositories of moduli‑space data, Strebel differential benchmarks, and Weil–Petersson volume calculators to standardize comparisons across methods.
- Sector: Policy/Infrastructure (open science), Academia, Software.
- Assumptions/dependencies: Funding for open computational infrastructure; shared data standards.
Long‑Term Applications
These require notable extensions: beyond scalar theories, inclusion of backreaction/renormalization in the emergent string, handling momentum‑dependent vertices, fermions/gauge fields, and developing scalable numerical algorithms.
- Automated derivation of holographic duals from generic QFT data
- Use case: A pipeline from a Lagrangian (including interactions, spin, gauge symmetry, masses) to an emergent non‑critical string description with a Liouville/holographic direction, valid at fixed genus and resummed in loop order; ultimately, a practical “QFT→String dual finder.”
- Sector: Academia (HEP, quantum gravity), Potentially Condensed Matter (applied holography).
- Tools/products:
- QFT2String: software that ingests QFT Feynman rules and outputs worldsheet CFT ingredients, boundary states, Liouville sector specifications, and moduli‑space integrators.
- Assumptions/dependencies: Generalization beyond massless momentum‑independent scalar propagators; inclusion of spin, gauge, and momentum structures; rigorous control of anomalies; matching to known dualities.
- Precision holography for strongly coupled observables
- Use case: Compute observables (correlators, transport, spectra) at strong coupling by resumming fixed‑genus contributions and incorporating gravitational backreaction (as renormalization) to stabilize backgrounds (e.g., toward AdS); support precision holography in phenomenology or condensed‑matter analogs.
- Sector: Academia (HEP/AdS/CFT), Condensed Matter (AdS/CMT), HPC.
- Tools/workflows:
- DegenRenorm Engine: implements backreaction=renormalization equivalence to renormalize worldsheet integrals via degeneration analysis; couples to background reconstruction.
- Assumptions/dependencies: Backreaction not yet implemented; requires solving coupled worldsheet‑background equations; potentially large computational costs.
- Generalized worldsheet encodings for realistic QFTs
- Use case: Extend the CFT construction (including ghosts/Liouville) to accommodate fermions, gauge fields, momentum‑dependent vertices, and masses; build a universal catalog of vertex/boundary state operators reproducing broad classes of Feynman rules.
- Sector: Academia (QFT, string theory), Software.
- Tools/workflows:
- WorldsheetOperatorCatalog: a library of operator insertions and boundary states reproducing diverse QFT interactions under the moduli‑space mapping.
- Assumptions/dependencies: Handling of spin structures on Riemann surfaces; anomaly cancellation; non‑trivial determinant factors; careful treatment of zero modes.
- New renormalization paradigms from geometric/degeneration viewpoints
- Use case: Develop renormalization schemes where counterterms are systematically derived from specific worldsheet degeneration channels; may simplify multi‑scale problems and improve resummation techniques.
- Sector: Academia (QFT methods), Software (symbolic/numeric).
- Tools/workflows:
- Geometry‑Guided RG: tools that translate geometric degenerations into RG flows/counterterms and automate consistency checks across genera.
- Assumptions/dependencies: Robust mapping for non‑scalar theories; interplay with conventional RG methods.
- Scalable moduli‑space numerics and data resources
- Use case: Build high‑performance algorithms for integration on M_{g,n} with realistic measures (Kontsevich/Weil–Petersson limits, determinants), including near‑degeneration regions; create benchmark datasets for amplitudes at fixed genus.
- Sector: Software (HPC), Academia.
- Tools/workflows:
- ModuliHPC: domain‑decomposition and importance‑sampling schemes tailored to degeneration boundaries; surrogate models/ML for integrand acceleration.
- Assumptions/dependencies: Efficient and accurate computation of Strebel differentials; stable determinant evaluations on families of surfaces; treatment of large genus and many punctures.
- Cross‑fertilization with mathematics and matrix‑model techniques
- Use case: Use the mapping to compute intersection numbers/volumes, study new relations among matrix models, 2D gravity, and moduli spaces; inform topological recursion and enumerative geometry.
- Sector: Academia (mathematics/physics interface).
- Assumptions/dependencies: Mathematical rigor for ultralocal bi‑local field devices; convergence and uniqueness issues.
- Potential quantum‑computing/algorithmic spin‑offs (speculative)
- Use case: Explore whether sampling over moduli spaces or genus expansions can inspire quantum/classical hybrid algorithms for amplitude estimation or complex integral evaluation.
- Sector: Software/Quantum Computing (speculative).
- Assumptions/dependencies: Significant algorithmic development; identification of quantum advantage regimes; adaptivity to degeneration‑dominated regions.
Key assumptions and dependencies across applications
- Theory scope: Initial construction targets massless scalar QFTs with momentum‑independent vertices; generalization to gauge fields, fermions, and momentum dependence is non‑trivial and is future work.
- Large‑N/topological organization: Practical control over the genus expansion is clearest in large‑N limits; outside large‑N, topological organization may be less predictive.
- Strebel differential numerics: Efficient and accurate computation of Strebel differentials (and associated metrics) on Riemann surfaces is required; existing algorithms are specialized and may need significant development.
- Anomalies and non‑critical strings: The worldsheet theory is non‑critical with a Liouville mode; careful handling of the ghost/Liouville sectors and central charge is needed to ensure consistency.
- Backreaction and renormalization: The paper identifies a correspondence but does not include gravitational backreaction; implementing this is essential for predictive backgrounds (e.g., AdS) and for fully renormalized results.
- Determinants and boundary conditions: Robust evaluation of determinants (ghost, Laplacian) with appropriate boundary conditions is crucial, especially near degenerations; zero‑mode treatment affects normalization and matching.
- Formal auxiliary devices: Ultralocal bi‑local fields and large‑N matrix auxiliaries function as generating tools for combinatorics; physical interpretation is formal/algorithmic, which is acceptable for software pipelines but may limit direct physical modeling.
- Computational cost: Integration over moduli spaces, evaluation of determinants, and handling of degeneration regions are computationally intensive; HPC and specialized numerics are likely necessary for realistic problems.
Overall, the paper provides a concrete, geometry‑first framework to reorganize and compute QFT amplitudes and a principled route toward emergent string descriptions. Immediate applications focus on research software, diagnostics, and pedagogy. Long‑term applications aim at automated dual construction and precision holography, contingent on substantive theoretical and computational advances.
Collections
Sign up for free to add this paper to one or more collections.