The Mean-Field Dynamics of Transformers (2512.01868v1)
Abstract: We develop a mathematical framework that interprets Transformer attention as an interacting particle system and studies its continuum (mean-field) limits. By idealizing attention continuous on the sphere, we connect Transformer dynamics to Wasserstein gradient flows, synchronization models (Kuramoto), and mean-shift clustering. Central to our results is a global clustering phenomenon whereby tokens cluster asymptotically after long metastable states where they are arranged into multiple clusters. We further analyze a tractable equiangular reduction to obtain exact clustering rates, show how commonly used normalization schemes alter contraction speeds, and identify a phase transition for long-context attention. The results highlight both the mechanisms that drive representation collapse and the regimes that preserve expressive, multi-cluster structure in deep attention architectures.
Sponsor
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
Overview
This paper asks a simple question about Transformers, the AI models behind tools like chatbots: if attention is the way tokens (like words) look at each other and combine information, what happens to those tokens as we pass through many attention layers? The authors build a clean mathematical model of attention and show that tokens often end up clustering together, sometimes slowly and in stages, and they explain when this happens, how fast it happens, and how to prevent “too much” clustering so the model stays expressive.
The big questions
The paper explores these easy-to-understand questions:
- How can we describe attention mathematically, in a way that still captures its most important behavior?
- Do tokens tend to group into clusters over time when we apply attention repeatedly?
- How fast do they cluster, and what controls that speed?
- What features of Transformer design (like normalization or sequence length) change this clustering behavior?
- Can we predict phase transitions—sharp changes—in behavior when we scale to very long sequences?
- What happens when we add noise (randomness) to attention?
How they studied it
To keep things clear and analyzable, the authors paper simplified versions of attention using everyday ideas and analogies:
- Tokens as particles on a sphere:
- Imagine each token is a point on the surface of a ball. This “sphere” idea mimics layer normalization, which keeps token lengths under control.
- Attention as “weighted averaging”:
- Each token points more strongly toward other tokens it finds similar. The weights come from how similar they are. A “temperature” parameter, called β (beta), controls how picky attention is. High β means the token focuses more on the most similar neighbors; low β spreads its attention more evenly.
- Two core models:
- SA (Self-Attention with normalization): tokens stay on the sphere and move along it toward a weighted average of other tokens.
- USA (Unnormalized Self-Attention): tokens move toward their weighted average without the sphere constraint, which is easier to analyze but less realistic.
- Mean-field viewpoint (crowd behavior):
- Instead of tracking every single token, they describe the flow of a whole crowd of tokens with a “continuity equation,” like tracking water flowing in a river. This approach reveals neat structure: in USA, the crowd moves downhill along an “energy landscape,” which is called a Wasserstein gradient flow. You can think of this like marbles rolling down a shaped surface toward lower energy.
- Synchronization analogy (Kuramoto model):
- In 2D (the circle), the dynamics look like a classic model where many pendulums try to tick in sync. This gives intuition for why attention tends to make tokens align or cluster.
- Metastability (long pauses near almost-stable states):
- Tokens often settle into multiple clusters that last for a very long time before merging into fewer, larger clusters. Think of balls settling into shallow bowls on a hillside; they sit there for ages before a small push sends them into the deeper valley below.
- Equiangular reduction (a one-number summary):
- If all token pairs start with the same similarity, the whole system can be reduced to tracking that single similarity over time. This makes it possible to get exact formulas for how fast tokens cluster.
- Normalization viewed as speed control:
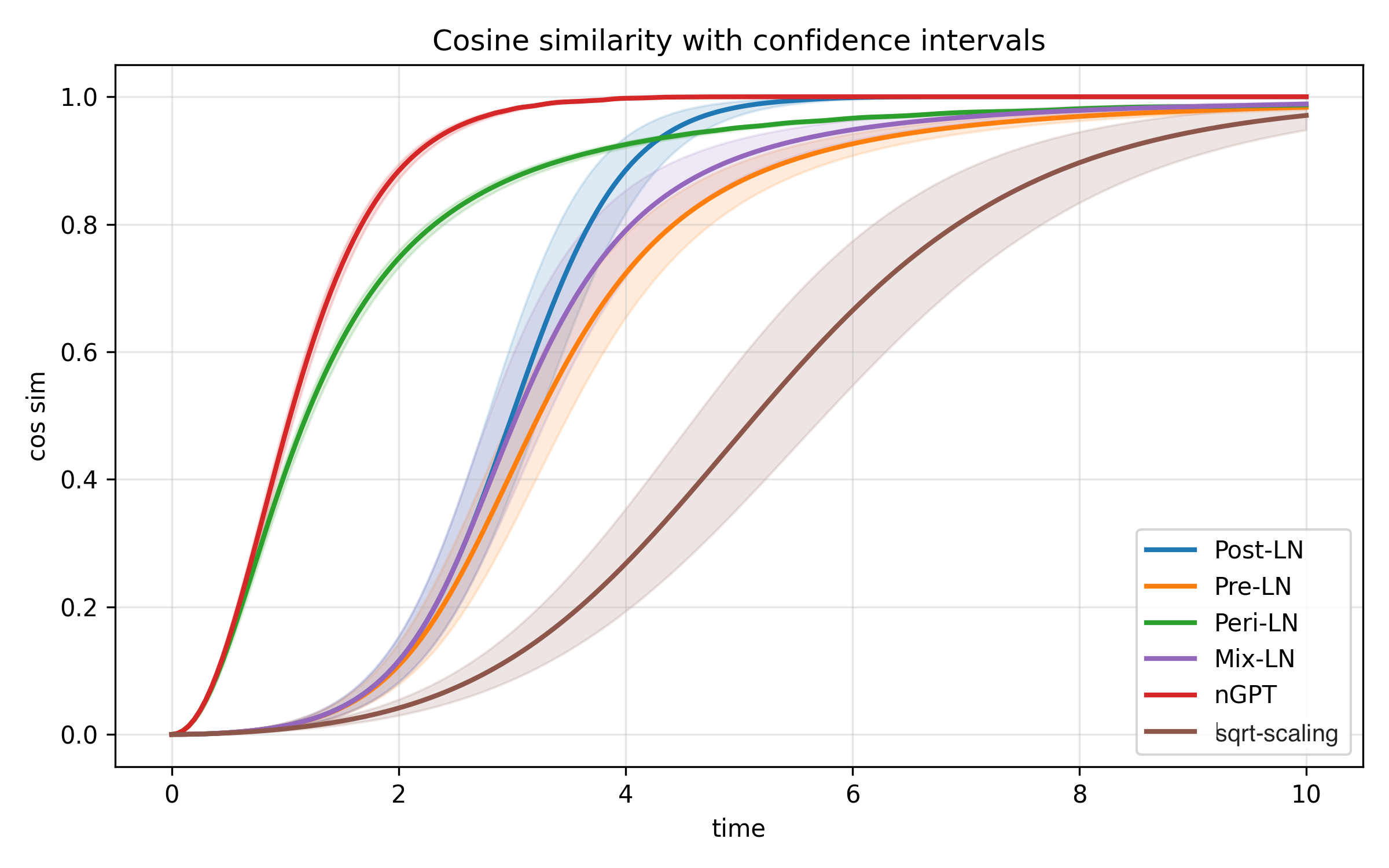
- Different layer normalization rules change how fast tokens move on the sphere. Pre-LN slows tokens, while Post-LN lets them move faster. This matters for avoiding “representation collapse,” where everything becomes too similar too soon.
- Long-context scaling:
- For very long sequences, attention scores flatten unless β is increased. The authors show that setting β proportional to log(n) (where n is sequence length) causes a phase transition: depending on the constant factor, attention either averages everything, preserves structure, or behaves close to identity.
Main findings and why they matter
Here are the core findings, explained simply:
- Clustering happens broadly:
- For most starting positions and dimensions , both SA and USA eventually make all tokens collapse into a single cluster. This matches what people see in real Transformers: token similarities increase layer by layer.
- Clustering can be fast or slow:
- If tokens begin in the same hemisphere (roughly, pointing in the same general direction), they collapse exponentially fast.
- In the mean-field (crowd) limit, when β is small, the collapse also happens at an exponential rate.
- As β grows, the landscape gets more complicated, and multiple clusters can appear and persist for very long times (metastability).
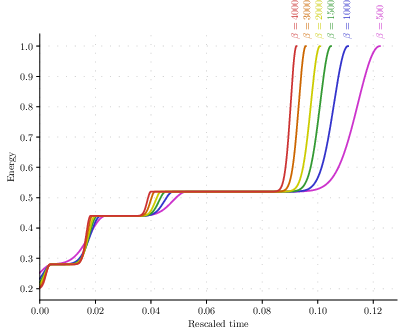
- Metastable multi-cluster states last exponentially long in β:
- Tokens quickly form several clusters and then sit in those configurations for an extremely long time, merging step by step. The energy over time looks like a staircase: long flat plateaus and sudden jumps when clusters merge.
- “Closest clusters merge first” at high β:
- In the hard-attention limit (very large β), the pair of clusters that are most similar merge first, on a much faster timescale than all other interactions.
- Attention is like Mean-Shift clustering on the sphere:
- SA matches a well-known clustering algorithm (Mean-Shift) when you blur the data at each step. This connection helps explain the formation and number of early clusters.
- Equiangular model gives exact rates:
- With symmetric starting similarities, SA contracts at a fixed exponential rate, while USA’s rate grows exponentially with β. This shows how normalization changes the speed of collapse.
- Normalization shapes depth behavior:
- Pre-LN slows down collapse (polynomial rate like ), which helps deep networks preserve useful diversity longer.
- Post-LN collapses faster (exponential rate like ), which can risk losing expressiveness if the model is very deep.
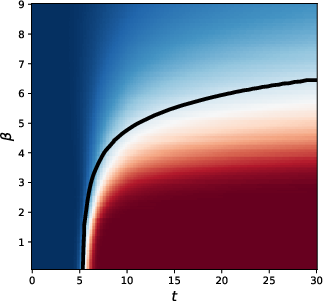
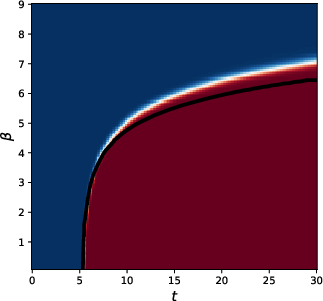
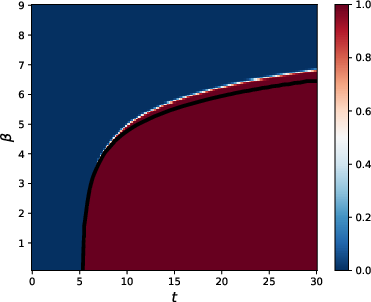
- Long-context phase transition:
- If β scales like βn = γ log n, there are three regimes:
- Subcritical γ: attention averages broadly and directions become almost identical (collapse).
- Critical γ: attention is sparse but structured—enough mixing without collapsing.
- Supercritical γ: attention acts almost like identity, preserving the input structure but mixing little.
- This explains why practical systems often choose β proportional to log(n): it avoids both full averaging and no mixing.
- Noise can be modeled and understood:
- Adding randomness leads to a stochastic version of the dynamics. As noise weakens, you return to the deterministic case. This opens the door to studying robustness and exploration.
Implications and potential impact
This mathematical picture has practical consequences for building better Transformers:
- Understanding representation collapse:
- Clustering is natural and expected. But collapsing too quickly or too completely hurts the model’s ability to represent complex patterns. This framework shows why it happens and how to control it.
- Choosing normalization wisely:
- Pre-LN slows contraction and uses depth effectively, keeping tokens diverse longer. This explains why many high-performing models prefer Pre-LN.
- Tuning β for long sequences:
- Scaling β with log(n) creates a “just right” regime that prevents collapse while preserving meaningful attention. This is crucial for long-context models.
- Designing architectures for multi-cluster expressiveness:
- Since useful representations often require multiple stable clusters, understanding metastability helps design attention blocks that maintain richness across layers.
- Connecting AI with physics and math:
- Viewing attention as particles on a sphere sliding down an energy landscape, synchronizing like oscillators, or clustering like Mean-Shift creates new analysis tools and new ways to reason about model behavior.
In short, the paper offers a clear, mathematically grounded explanation of why and how attention causes tokens to cluster, shows how design choices change the speed and structure of this clustering, and gives practical guidance for building stable, expressive Transformers—especially for deep or long-context settings.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a single, concrete list of unresolved issues, limitations, and open problems that emerge from the paper’s modeling choices, results, and scope.
- Rigorous PDE limits for SA: The paper states that the SA mean-field continuity equation “converges formally to a reverse heat equation” (large-) and to a porous medium type equation after rescaling; a full, rigorous derivation (well-posedness, scaling regimes, uniqueness, and stability) of these limits remains open.
- Global quantitative rates for finite systems: Beyond the hemisphere condition in Theorem 4.2, obtain explicit global rates of clustering for SA/USA as functions of and initial separation, including sharp constants and matching lower bounds.
- Complete coverage of and all : The case is only partially addressed (recent results for ). A full characterization of synchronization and rates for all in remains to be established.
- Large- mean-field regime: Theorem 4.4 provides exponential convergence for small ; quantitatively characterizing convergence, metastability, and possible multi-cluster equilibria for large at mean-field (including thresholds and rates) is an open problem.
- Energy landscape classification: Provide a complete classification of critical points of the interaction energy (Equation (3)), including their indices, stable/unstable manifold dimensions, and heteroclinic connections, for general , , and .
- Metastable lifetimes and coarsening laws: Quantify the exponentially long metastable timescales (precise dependence of , on and on inter-cluster distances), derive coarsening exponents, and provide sharp bounds on saddle-to-saddle transition times (beyond asymptotic ).
- Degenerate closest-pair cases in hardmax limit: Theorem 5.1 assumes a unique closest pair. Analyze tie cases (multiple closest pairs), determine selection dynamics, and quantify how small perturbations or noise break degeneracy in the large- regime.
- General parameter matrices (learned Q, K, V): Most results idealize . Extend clustering, metastability, and phase-transition analyses to anisotropic kernels induced by learned , characterizing when parameters amplify or suppress collapse.
- Multi-head attention: Develop a theory for heads with distinct kernels operating in parallel, including conditions under which multi-headed interactions delay collapse, create persistent multi-cluster structure, or induce new phase transitions.
- Feed-forward blocks and residuals: Incorporate MLP dynamics and residual connections into the interacting-particle framework, and quantify how they counteract or amplify attention-driven contraction and clustering over depth.
- Normalization beyond equiangular: The unified speed-regulation model for LN variants yields rates under equiangular initializations; extend to non-equiangular, random, and task-driven initializations, proving general collapse rates and identifying regimes that preserve multi-cluster structure.
- Design of speed regulation to avoid collapse: Characterize principled choices of speed factors (Section 6.2) that provably maintain multi-cluster representations over many layers while ensuring stability, and provide bounds linking , , and depth to guaranteed minimal diversity.
- Long-context phase transition beyond equiangular: Theorem 6.1 is for equiangular inputs and a single attention layer. Extend to random or structured initializations, multiple layers, multi-head settings, and trained weights; characterize critical and contraction profiles in these more realistic regimes.
- Dimensional effects: Quantify how affects clustering rates, metastable cluster counts, and phase boundaries; provide finite- corrections to equiangular predictions derived from concentration-of-measure heuristics.
- Mean-Shift connection in high dimensions: The KDE mode-count analysis is presently 1D. Extend the mode-count and metastable-cluster predictions to spheres () for the attention kernel , including concentration and criticality thresholds.
- Weighted tokens (Wasserstein–Fisher–Rao flows): The paper notes clustering under dynamic reweighting but lacks rates and metastability analysis; develop quantitative convergence and coarsening results for the WFR-coupled dynamics.
- Noise and stochastic dynamics: The noisy Transformer SDE (Section 7) is introduced but not analyzed. Establish existence/uniqueness, invariant measures, phase diagrams in , noise-induced escape times from metastable states, and large-deviation rates for saddle-to-saddle transitions.
- Causal attention (decoder): Extend the analysis to causal masking, quantifying how temporal asymmetry affects clustering, metastability, and long-context phase transitions.
- Negative temperatures (): Characterize the repulsive regime (anti-attention), including possible de-clustering, dispersion rates, and whether stable multi-cluster or uniform states emerge.
- Empirical validation and measurement: Provide quantitative comparisons between theory and pretrained models (e.g., cluster counts per layer, contraction rates, metastable lifetimes), and standardized diagnostics for representation collapse in practice.
- Training dynamics of parameters: Move beyond fixed kernels to paper co-evolution of tokens and parameters under gradient-based training, determining when training avoids collapse, preserves multi-cluster structure, or selects particular metastable states.
- Robustness to architectural extensions: Analyze how sparse/long-range attention, mixture-of-experts routing, and hierarchical structures modify the mean-field dynamics and energy landscape, including conditions preventing collapse in these extended architectures.
- Computational methods for metastability: Develop scalable algorithms to detect, quantify, and control metastable multi-cluster states in high-dimensional attention flows, with certified error bounds and stopping criteria.
Glossary
- Brownian motion (on the sphere): A continuous-time stochastic process describing random motion constrained to the sphere’s surface. "and are independent Brownian motions on ."
- Center-stable manifold theorem: A result describing the structure of sets attracted to equilibria with non-expanding directions in dynamical systems. "By the center-stable manifold theorem~\cite[Thm.~III.7]{shub2013global}, the set of initial conditions whose trajectories converge to such saddles is contained in a countable union of lower-dimensional manifolds and thus has measure zero."
- Concentration of measure: A phenomenon in high dimensions where random points concentrate around mean values, making inner products near zero. "As , random points on the sphere become almost orthogonal by concentration of measure:"
- Continuity equation: A PDE expressing conservation of mass for evolving probability measures under a velocity field. "and evolves according to the mean-field continuity equation"
- Dirac mass: A probability measure concentrated at a single point. "converges weakly to a Dirac mass supported at some point $x_\infty\inS^{d-1}$."
- Edgeworth expansions: Asymptotic series refining the central limit theorem to approximate distributions more accurately. "Using Edgeworth expansions and the KacâRice formula, we can show that is of order "
- Equiangular model: A symmetry-reduced model where all pairwise inner products are equal, yielding a one-dimensional dynamics for correlations. "Section~\ref{sec:equiangular} introduces the equiangular model, which provides a tractable one-dimensional reduction capturing clustering rates, the effect of normalization, and the phase transition in long-context Transformers."
- Geodesic: The shortest path on a manifold (here, the great-circle path on the sphere). "move along the unique geodesic connecting them and merge in finite rescaled time."
- Grönwall argument: A technique using Grönwall’s inequality to bound solutions of differential inequalities. "In fact, using a Gr\"onwall argument, one obtains exponential convergence to a single cluster as soon as all tokens initially lie in a common open hemisphere."
- Hardmax-like dynamics: A limiting regime where attention concentrates on the single most similar token, approximating an argmax (hard selection). "a final pairing phase governed by hardmax-like dynamics~\cite{hardmax}, during which the two closest clusters merge."
- Heteroclinic orbits: Trajectories connecting distinct saddle points in a dynamical system. "connected by heteroclinic orbits that describe the gradual merging of clusters."
- Interacting particle system: A model where particles evolve with velocities depending on the states of other particles. "Transformer attention as an interacting particle system"
- Kac–Rice formula: A tool to compute the expected number of critical points of random fields. "Using Edgeworth expansions and the KacâRice formula"
- Kernel density estimator (KDE): A nonparametric estimator of a probability density via averaging kernel bumps over data points. "the Mean-Shift algorithm defines clusters as basins of attraction of the modes of a kernel density estimator (KDE)"
- Kuramoto model: A canonical system for synchronization of coupled oscillators on the circle. "the classical (homogeneous) Kuramoto model~\cite{kuramoto1975self, acebron2005kuramoto}"
- Logarithmic attention scaling: Growing the attention temperature proportionally to log sequence length to avoid uniform averaging in long contexts. "adopt a logarithmic attention scaling ."
- McKean–Vlasov SDE: A stochastic differential equation where the drift depends on the solution’s current law. "the empirical distribution of the system converges to the solution of the McKean--Vlasov SDE"
- McKean–Vlasov type: Refers to mean-field equations whose coefficients depend on the evolving distribution. "the equation is nonlinear and of McKeanâVlasov type."
- Mean-field dynamics: The evolution where each particle interacts with the aggregate (empirical) distribution of all particles. "This situates Transformers within the broad mathematical framework of mean-field dynamics."
- Mean-field limit: The continuum limit as the number of particles grows, yielding a PDE or measure-valued flow. "continuum (mean-field) limits."
- Mean-Shift clustering: An algorithm that moves points along the gradient of a kernel density estimate to cluster at modes. "The dynamics~\eqref{eq:SA} are closely related to a continuous-time analogue of the classical Mean-Shift clustering algorithm."
- Metastability: Long-lived intermediate states where evolution is extremely slow before transitioning to the final equilibrium. "Metastability and the formation of multiple clusters."
- Polyak–Łojasiewicz inequality: A condition relating function suboptimality to gradient norm that yields convergence rates for gradient flows. "a Polyak--{\L}ojasiewicz-type inequality near "
- Porous medium equation: A nonlinear diffusion PDE with degenerate diffusivity, modeling slower spreading than heat flow. "it converges to a porous medium type equation"
- Reverse heat equation: A formal anti-diffusive limit where mass concentrates rather than spreads. "converges formally to a reverse heat equation."
- Riemannian gradient: The gradient defined with respect to a manifold’s metric (here, the sphere). "interpreting as the Riemannian gradient on the sphere"
- Saddle-to-saddle dynamics: Evolution that lingers near a sequence of saddle points with sharp transitions between them. "Saddle-to-saddle dynamics and the staircase profile."
- Softmax (velocity field): The attention-induced vector field where weights are exponentials normalized across tokens. "the softmax velocity field in~\eqref{eq:SA} converges"
- Synchronization: The process where system components align to a common state or phase. "the classical framework to paper synchronization"
- Tangent space: The vector space of directions tangent to a manifold at a point. "denotes the orthogonal projection onto ."
- Torus (one-dimensional): The circle represented as the interval with endpoints identified. "where denotes the one-dimensional torus"
- Wasserstein gradient flow: Gradient flow of an energy functional with respect to the Wasserstein metric on probability measures. "is the Wasserstein gradient flow~\cite{ambrosio2005gradient, CheNilRig25} of the interaction energy"
- Wasserstein–Fisher–Rao gradient flow: A gradient flow combining transport (Wasserstein) and mass change (Fisher–Rao) effects. "weighted tokens that evolve according to the Wasserstein-Fisher-Rao gradient flow whereby particles evolve and are also dynamically reweighted"
- Weak convergence: Convergence of probability measures tested against bounded continuous functions. "converges weakly to a Dirac mass"
Practical Applications
Overview
The paper develops a mathematically grounded view of Transformer attention as an interacting particle system with mean-field limits, connecting it to Wasserstein gradient flows, synchronization (Kuramoto), and mean-shift clustering. It proves global clustering (representation collapse) under broad conditions, quantifies rates via a tractable equiangular reduction, shows how normalization (Pre-LN vs Post-LN and variants) regulates contraction speed, and identifies a phase transition for long-context attention when the temperature scales as a logarithm of sequence length. These insights support concrete applications in model design, training, diagnostics, and long-context stability.
Below are actionable applications grouped into immediate and long-term, with sector references, potential tools/products/workflows, and key assumptions or dependencies.
Immediate Applications
The following can be deployed now with moderate engineering and validation effort.
- Temperature scaling for long-context stability — Sectors: software/LLMs, education, healthcare, legal
- Use the paper’s phase transition result to set attention temperature β as βn = γ log n, and keep γ near the critical regime γ ≈ 1/(1 − ρ) (ρ is average inter-token cosine) to avoid uniform averaging and collapse while preserving sparse mixing.
- Tool/workflow: “Context-Aware Temperature Scaler” that estimates ρ on-the-fly per batch/layer and sets βn; deployable as a training-time callback or inference-time knob for long documents/EHRs/long transcripts.
- Assumptions/dependencies: Equiangular reduction approximates early-layer behavior; requires reliable estimation of ρ; multi-head and MLP interactions may modulate effects.
- Normalization scheme selection to manage contraction speed — Sectors: software/LLMs
- Prefer Pre-LN (or speed-regulated LN variants) for deep stacks to slow directional contraction (polynomial decay ~1/t² vs exponential for Post-LN), preserving expressive multi-cluster structure longer.
- Tool/workflow: Unified LN “speed regulator” implementation that exposes the s_i(t) factor per token (Post-LN: s_i=1; Pre-LN: s_i=‖x_i‖; Peri-LN/Mix-LN/ngpt/sqrt-scaling mapped to s_i variants); accompanied by automated unit tests on clustering rates using equiangular diagnostics.
- Assumptions/dependencies: Results derived on SA/USA abstractions; real models have Q/K/V/MLP/residuals; still empirically aligns with practice (e.g., GPT/LLaMA pre-LN).
- Representation collapse monitoring and alerts — Sectors: software/LLMs, MLOps
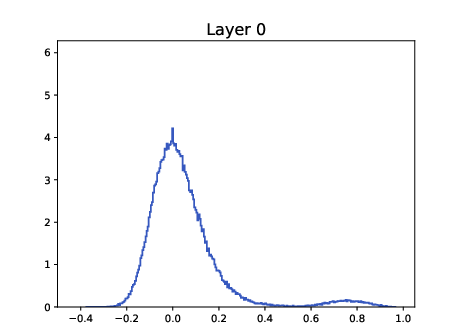
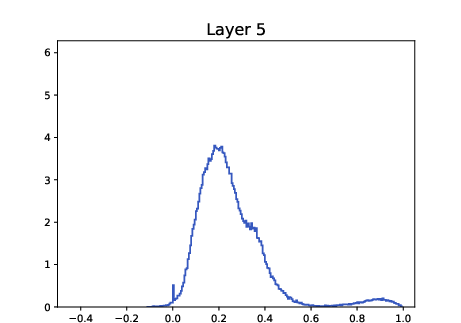
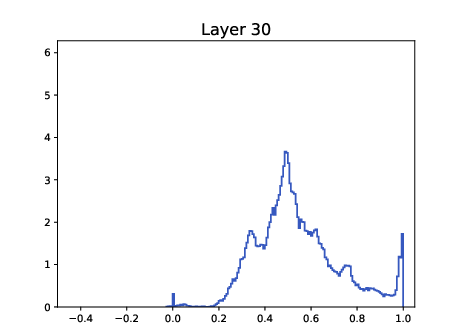
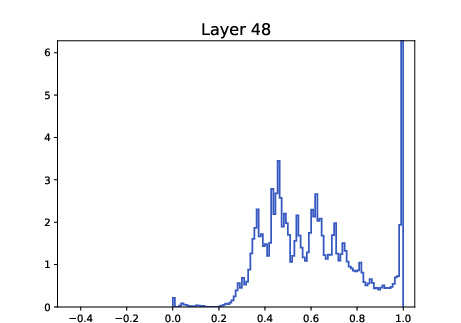
- Track pairwise cosine distributions across layers to detect metastable multi-cluster formation and dangerous drift toward single-cluster collapse (as in ALBERT histogram evidence).
- Tool/workflow: “Clustering Dashboard” with per-layer histograms of ⟨xi, xj⟩, cluster-count proxies (e.g., modality of KDE on the sphere), and alarms for over-contraction; integrate with training pipelines for early stopping or β/LN schedule adjustments.
- Assumptions/dependencies: Access to intermediate embeddings; compute overhead manageable; metrics sensitive to tokenization and task distribution.
- β schedules to shape expressivity over depth — Sectors: software/LLMs
- Start from smaller β in early/mid layers to encourage multi-cluster metastable structure; optionally increase later to consolidate; or keep β modest to avoid anti-diffusive regimes that over-fragment then collapse.
- Tool/workflow: “Attention Phase Controller” that schedules β by layer depth and observed ρ; supports per-head β if needed.
- Assumptions/dependencies: Small-β mean-field guarantees and metastability insights; tuning may be task-specific.
- Cluster-aware token routing in Mixture-of-Experts (MoE) — Sectors: software/LLMs
- Use attention-induced cluster structure to route tokens to specialists, reducing interference and preserving diversity before collapse.
- Tool/product: “ClusterRoute” MoE gate that derives clusters from attention/KDE on the sphere and routes clusters to stable experts, with guardrails that detect when clusters begin to merge.
- Assumptions/dependencies: Robust, low-latency clustering; interplay with expert capacity and load balancing.
- Mean-shift-inspired chunking for retrieval and summarization — Sectors: information retrieval/RAG, enterprise search
- Apply spherical mean-shift on token or sentence embeddings to merge semantically coherent spans, improving context windows and reducing redundancy.
- Tool/workflow: “Spherical Mean-Shift Chunker” with Gaussian kernel on the sphere; tune kernel bandwidth using β heuristics; deploy in preprocessing for RAG pipelines.
- Assumptions/dependencies: Embedding quality; choice of kernel bandwidth; domain-dependent evaluation.
- Long-context diagnostics and guardrails — Sectors: software/LLMs, compliance
- Measure γ relative to ρ to detect if attention is subcritical (averaging and collapse risk), critical (sparse mixing sweet spot), or supercritical (identity-like regime); adjust βn or add sparsity constraints accordingly.
- Tool/workflow: “Phase Regime Detector” that compares γ and 1/(1−ρ) per layer and suggests parameter tweaks.
- Assumptions/dependencies: Correct estimation of ρ; multi-head heterogeneity; task-level tolerances.
- Research tooling for dynamics simulation — Sectors: academia
- Provide open-source SA/USA simulators, equiangular ODE solvers, and PDE mean-field approximations to paper clustering, metastability, and LN speed regulation under controlled conditions.
- Tool/product: “Transformer Dynamics Lab” toolkit with reproducible experiments and visualizations of staircase energy profiles, saddle transitions, and Kuramoto reductions.
- Assumptions/dependencies: Educational/research setting; abstraction fidelity vs. full architectures.
Long-Term Applications
These require further research, scaling, or productization to reach robust deployment.
- Phase-aware attention architectures — Sectors: software/LLMs
- Design layers that maintain near-critical βn ≈ (log n)/ (1−ρ) with feedback control to preserve sparse mixing without collapse, potentially per head and per layer.
- Product: “Critical Attention” modules with dynamic β controllers and stability guarantees; combine with content-adaptive sparsity.
- Assumptions/dependencies: Robust estimators for ρ under nonstationary inputs; stability under training noise and MLP/residual interactions.
- Energy-regularized Transformers (gradient-flow design) — Sectors: software/LLMs
- Embed energy landscape constraints (Wasserstein gradient flow analogues) to bound contraction and prevent representation collapse, shaping the saddle hierarchy for desired coarsening behavior.
- Product: “Energy-Shaped Attention” layers with regularizers that control ∥∇Eβ∥ near multi-cluster manifolds (slow motion), preserving expressivity.
- Assumptions/dependencies: Differentiable energy proxies compatible with large-scale training; empirical trade-offs in accuracy, speed, and stability.
- Noise-injection schedules (Noisy Transformers) — Sectors: software/LLMs
- Use controlled stochasticity (SDE on the sphere with parameter κ) to counteract over-contraction and improve generalization/diversity, analogous to diffusion-inspired regularization.
- Product: “Stochastic Attention” with κ-annealing; evaluate on long-context tasks and robustness benchmarks.
- Assumptions/dependencies: Careful calibration to avoid degrading signal; alignment with optimizer and normalization dynamics.
- Automated hyperparameter design using equiangular/mean-field predictors — Sectors: software/LLMs, MLOps
- Build meta-optimizers that precompute contraction rates and clustering trajectories (using the equiangular ODE and small-β mean-field) to auto-tune β schedules, LN selection, and context scaling.
- Product: “Dynamics-Guided AutoTuner” integrating with training pipelines.
- Assumptions/dependencies: Model mismatch between abstractions and full stacks; head-wise variability.
- Cluster-preserving objectives and regularizers — Sectors: software/LLMs
- Penalize over-contraction (e.g., via diversity terms on cosine similarity distributions) or enforce minimum cluster counts at intermediate layers to sustain multi-cluster metastable states.
- Product: “Expressivity Guardrails” as loss terms or layer constraints; evaluate on reasoning, summarization, long-context retention.
- Assumptions/dependencies: Task-dependent optimal cluster count; possible trade-offs with accuracy.
- Explainability via cluster evolution — Sectors: software/LLMs, safety/fairness
- Visualize and quantify token cluster formation and coalescence across layers, linking multi-cluster phases to semantic abstraction stages and detecting minority signal suppression early.
- Product: “ClusterLens” explainability suite with curriculum-level insights; fairness probes that monitor whether minority-context tokens prematurely collapse.
- Assumptions/dependencies: Interpretability of clusters for complex inputs; evaluation frameworks for fairness/retention.
- Cross-domain synchronization and consensus algorithms — Sectors: robotics, sensor networks, energy
- Translate attention-inspired interaction rules and metastability control into multi-agent consensus protocols (e.g., Kuramoto-like coupling with speed regulation) for robust coordination with tunable coarsening phases.
- Product: “Consensus via Attention” libraries for swarm robotics or distributed sensing; stability proofs using mean-field dynamics.
- Assumptions/dependencies: Mapping from token interactions to physical agent coupling; communication constraints and delays.
- Policy and deployment guidelines for long-context LLMs — Sectors: policy/compliance
- Establish best practices to disclose attention scaling choices and collapse risk for long documents; require monitoring of representation diversity to mitigate over-summarization or loss of minority context.
- Workflow: “Long-Context Compliance Checklist” including βn setting, diversity metrics, and audit reports of cluster dynamics.
- Assumptions/dependencies: Standardization across vendors; measurable links between clustering metrics and user-level harms.
Notes on Assumptions and Dependencies
- Many results assume simplified SA/USA dynamics with spherical normalization, identity Q/K/V, and continuous-time flow; real models have multi-head, residuals, MLPs, and training noise.
- Equiangular reductions are most predictive in high dimensions or near-orthogonal initializations; early-layer behavior often approximates this.
- Mean-field rates hold under small β and density assumptions; large β introduces complex metastability and multi-cluster states.
- Long-context phase transition insights rely on estimating average cosine ρ; robust estimation per batch/layer/head is a practical requirement.
- Normalization choices (Pre-LN vs Post-LN and variants) map to speed regulation factors s_i(t), which affect directional contraction; empirical validation in target architectures is recommended.
Collections
Sign up for free to add this paper to one or more collections.