Multi-view diffusion geometry using intertwined diffusion trajectories (2512.01484v1)

Abstract: This paper introduces a comprehensive unified framework for constructing multi-view diffusion geometries through intertwined multi-view diffusion trajectories (MDTs), a class of inhomogeneous diffusion processes that iteratively combine the random walk operators of multiple data views. Each MDT defines a trajectory-dependent diffusion operator with a clear probabilistic and geometric interpretation, capturing over time the interplay between data views. Our formulation encompasses existing multi-view diffusion models, while providing new degrees of freedom for view interaction and fusion. We establish theoretical properties under mild assumptions, including ergodicity of both the point-wise operator and the process in itself. We also derive MDT-based diffusion distances, and associated embeddings via singular value decompositions. Finally, we propose various strategies for learning MDT operators within the defined operator space, guided by internal quality measures. Beyond enabling flexible model design, MDTs also offer a neutral baseline for evaluating diffusion-based approaches through comparison with randomly selected MDTs. Experiments show the practical impact of the MDT operators in a manifold learning and data clustering context.

• The paper introduces a novel formulation for multi-view diffusion using time-inhomogeneous random walk operators, establishing a unified framework for multi-modal data fusion.
• It leverages intertwined diffusion trajectories with optimization strategies like random sampling and convex methods to achieve robust manifold recovery and improved clustering performance.
• The approach generalizes traditional diffusion maps by offering enhanced control over local and global connectivity, validated on both synthetic and real-world datasets.

Multi-view Diffusion Geometry Using Intertwined Diffusion Trajectories

Introduction and Motivation

The paper "Multi-view diffusion geometry using intertwined diffusion trajectories" (2512.01484) presents a unified theoretical and algorithmic framework for multi-view representation learning rooted in the generalization of diffusion maps via Multi-view Diffusion Trajectories (MDTs). As multi-view datasets become ubiquitous in scientific and industrial domains—where observations from disparate modalities or sources are available—the challenge of fusing complementary, heterogeneous information becomes central. Traditional methods fuse views by constructing static composite operators (e.g., products or convex combinations of kernels), often lacking the flexibility to capture intricate relationships and information flows across modalities.

MDTs define fusion as a time-inhomogeneous process that sequentially intertwines operators from different views, forming a trajectory of random walk operators whose composite dynamics reflect both local and global cross-view connectivity. This formulation generalizes standard diffusion maps, Alternating Diffusion (AD), Integrated Diffusion (ID), and similar fusion strategies, while enabling principled operator learning driven by internal task-specific criteria.

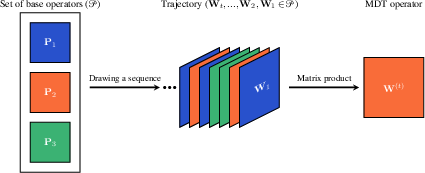
Figure 1: MDT operator construction as a left-product of a sequence of random walk operators drawn from different views, encoding the temporal interplay among modalities.

Theoretical Framework: Multi-view Diffusion Trajectories

MDT Formulation

Let $P$ denote a set of transition matrices, each representing a view-specific diffusion operator. An MDT is instantiated as a sequence $(_i)_{i=1}^t$ where each $_i \in P$, and the MDT operator for length $t$ is defined as the matrix product $^{(t)} = _t _{t-1} \cdots _1$. This encapsulates a time-inhomogeneous Markov chain over the data graph whose connectivity and mixing properties are determined by the choice and order of the operators.

The framework generalizes the single-view diffusion operator $^t$ (when $P$ contains only one element) to arbitrary compositions, supporting deterministic, randomized, or optimized selection policies for the trajectory.

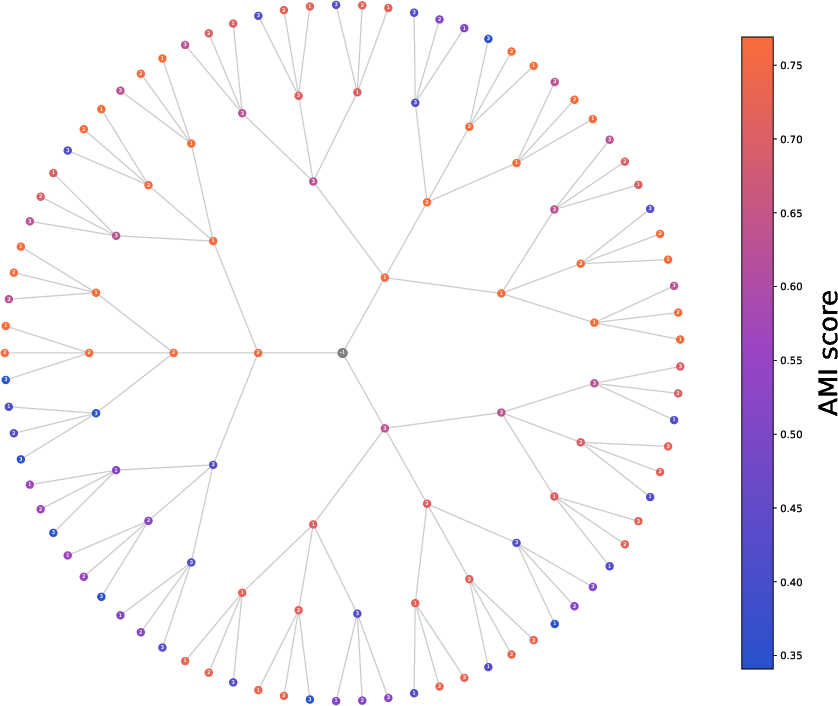
Figure 2: Tree representation of the MDT trajectory space for three views, where each path corresponds to a unique operator product sequence. Node color correlates with clustering performance, illustrating the effect of trajectory choice.

Fundamental Properties

Under mild conditions—i.e., all $P$ elements are irreducible, aperiodic row-stochastic matrices—the resulting MDT operator defines an irreducible, aperiodic, and ergodic Markov process. For any $t$, the product $^{(t)}$ admits a unique stationary distribution $\pi_t$, and the process converges to a rank-one stationary regime as $t\to \infty$. Unlike classical diffusion, the time-inhomogeneous trajectory provides more nuanced control over the scale and fusion of cross-view information.

Notably, $^{(t)}$ is generally non-symmetric and not self-adjoint, so embeddings derived from its SVD (rather than eigendecomposition) preserve trajectory-dependent diffusion distances.

Diffusion Geometry and Embeddings in the MDT Framework

Trajectory-dependent Diffusion Distance and Map

For each trajectory, the diffusion distance between datapoints $x_i$ and $x_j$ is

$$_{^{(t)}}(x_i, x_j) = \sum_{k=1}^{N}\frac{1}{\pi_t(k)}\big(^{(t)}_{ik}-^{(t)}_{jk}\big)^2,$$

generalizing the spectral smoothing, denoising, and metric preservation properties of single-view diffusion maps to arbitrary multi-view fusion paths.

The SVD of $^{(t)}$ yields trajectory-dependent embeddings, with the Euclidean distance in the embedded space exactly matching the defined diffusion distance.

Operator Learning and Trajectory Selection

Optimization Strategies

A major contribution of the framework is enabling unsupervised operator learning in the trajectory space, leveraging task-driven internal quality measures (e.g., clustering indices such as Calinski-Harabasz, contrastive embedding objectives) for guidance. Optimization can be realized via random sampling (MDT-Rand), beam search, convex combinations and gradient-based methods (MDT-Direct, MDT-Cvx), or continuous interpolation strategies, with flexible mechanisms for tuning the number of diffusion steps $t$ by spectral entropy heuristics.

Randomly sampled trajectories are advocated as neutral baselines for benchmarking, while trajectory optimization can adaptively weight, order, or repeat view operators to maximize downstream performance.

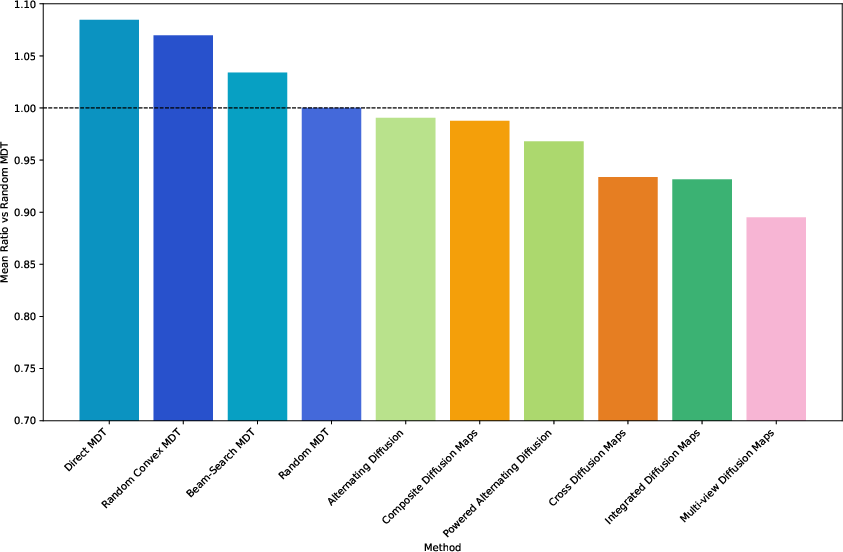
Figure 3: PRR index comparing clustering performance of various methods to MDT-Rand, underlining the competitive baseline strength of random MDTs relative to alternative diffusion fusion schemes.

Empirical Evaluation

Manifold Learning

MDT variants are rigorously benchmarked on nonlinear multi-view manifold recovery tasks using synthetic datasets (e.g., Helix-A, Helix-B, Deformed Plane) and contrastive criteria. MDT embeddings match or surpass those from AD, ID, and MVD, robustly capturing latent geometric structures even in the presence of view-specific distortions.

Clustering

Extensive experiments across real-world multi-view datasets (K-MvMNIST, L-MvMNIST, Olivetti, Yale, 100Leaves, L-Isolet, MSRC, Multi-Feat, Caltech101-7) show that MDT variants optimized in convex or discrete trajectory spaces generally yield higher adjusted mutual information (AMI) and stronger internal quality scores than fixed fusion approaches. Random MDTs provide robust reference points, often outperforming or closely matching more complex methods.

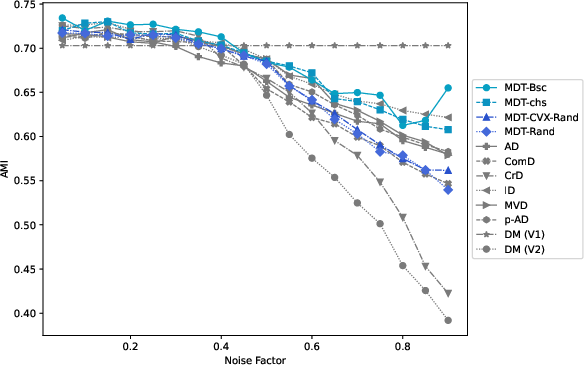
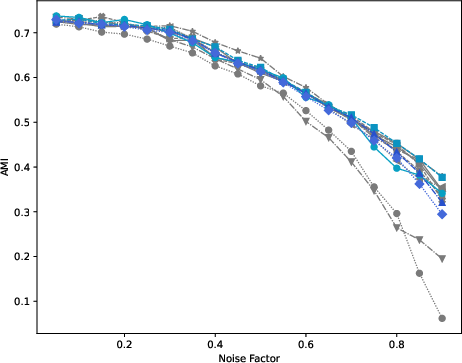
Figure 4: MDT-based clustering performance on K-MvMNIST, demonstrating resilience to increasing cross-view noise.

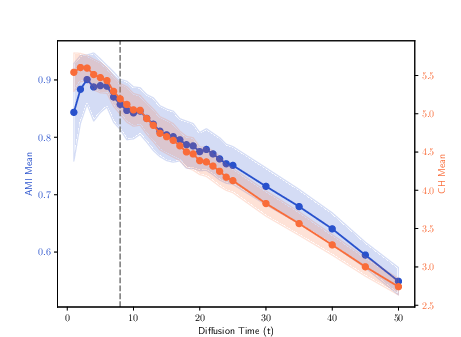
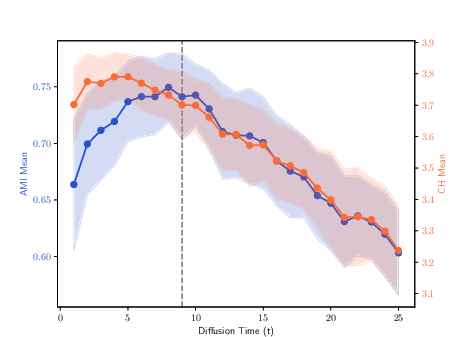
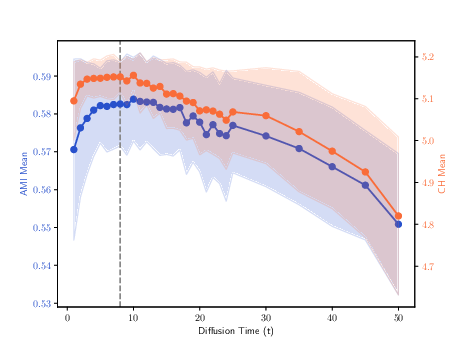
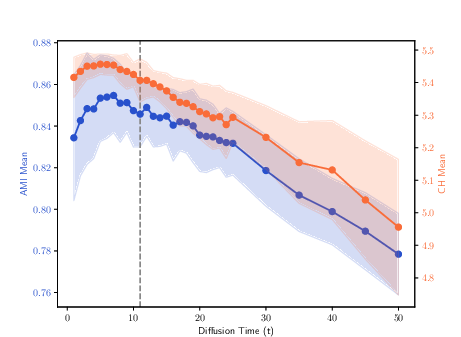
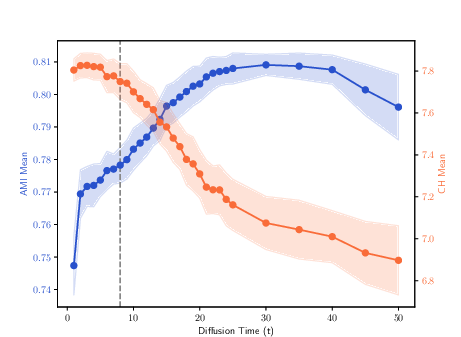
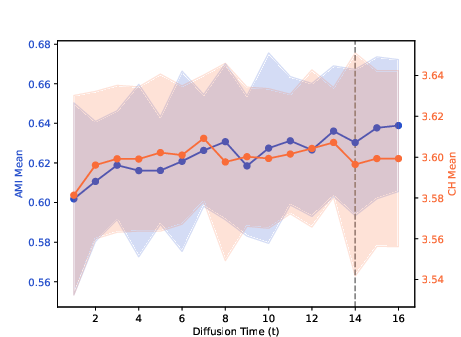
Figure 5: Clustering results for the 100Leaves dataset, highlighting the effect of MDT trajectory selection on complex multi-class data.

Implications and Future Directions

Practical Implications

MDTs present a scalable, flexible baseline and advanced tool for multi-view representation learning in manifold learning, clustering, and possibly semi-supervised or supervised fusion scenarios. Their operator learning capabilities allow adaptive response to view reliability, noise, or informativeness, bypassing the rigid rules of prior composite kernel methods.

Theoretical Extensions

The unified probabilistic formulation naturally integrates and subsumes numerous prior operator-based fusion models, offering a common language for analysis and comparison. Continuous-time analogs (potentially linking to heat kernels and more general geometric flows), supervised extensions, more expressive operator sets (including localized or attention-weighted variants), and connections to neural graph-based methods are compelling avenues for further research.

Conclusion

Multi-view Diffusion Trajectories generalize and unify diffusion geometry in multi-modal settings, offering theoretically solid, algorithmically powerful, and empirically validated fusion mechanisms. The ability to learn, optimize, and adapt trajectories in operator space fundamentally enhances the granularity and effectiveness of multi-view data representation and fusion. MDTs should be considered essential baselines and starting points in the development and evaluation of future multi-view learning systems.