Multilayer network science: theory, methods, and applications (2511.23371v1)
Abstract: Multilayer network science has emerged as a central framework for analysing interconnected and interdependent complex systems. Its relevance has grown substantially with the increasing availability of rich, heterogeneous data, which makes it possible to uncover and exploit the inherently multilayered organisation of many real-world networks. In this review, we summarise recent developments in the field. On the theoretical and methodological front, we outline core concepts and survey advances in community detection, dynamical processes, temporal networks, higher-order interactions, and machine-learning-based approaches. On the application side, we discuss progress across diverse domains, including interdependent infrastructures, spreading dynamics, computational social science, economic and financial systems, ecological and climate networks, science-of-science studies, network medicine, and network neuroscience. We conclude with a forward-looking perspective, emphasizing the need for standardized datasets and software, deeper integration of temporal and higher-order structures, and a transition toward genuinely predictive models of complex systems.
Sponsor
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
What is this paper about?
This paper is a big-picture guide to “multilayer networks.” It explains how to paper complicated systems—like social media, power grids, the internet, the brain, or ecosystems—where the same things (people, machines, species, brain regions) are connected in more than one way at the same time. Instead of using just one map of connections, multilayer networks use several layers (like different maps stacked together), one for each type of connection or each moment in time. The paper reviews the main ideas, tools, and real-world uses of this approach.
What questions are the authors asking?
In simple terms, the authors ask:
- How should we describe and measure systems that have many types of connections at once?
- How do we find meaningful groups (communities) in these multilayer systems?
- How do processes like spreading diseases, sharing information, or synchronizing behavior work when multiple layers interact?
- How do time and group interactions (more than two at once) change what we see?
- Where is this useful in the real world (infrastructure, health, finance, climate, and more)?
- What’s missing right now, and what should researchers build next (like shared datasets, software, and better predictive models)?
How did they paper it?
This is a review paper. That means the authors did not run one new experiment; instead, they read and organized many recent studies to explain the current “state of the art.” They also lay out common language, methods, and open problems so others can build on them.
The building blocks (with simple analogies)
- Nodes and links: Think of nodes as “things” (people, stations, websites) and links as “connections” (friendships, cables, roads).
- Layers: Imagine different layers like different apps you use (texting, gaming, video calls). The same person appears in each app, but the connections differ. Stacking these gives a multilayer network.
- Interlayer links: These connect the same node across layers (your account on different apps), or different nodes across layers (a power station relying on an internet server).
Core tools (explained in everyday terms)
- Adjacency matrix and “supra-adjacency” matrix: These are big tables that record who is connected to whom. A supra-adjacency matrix is like one giant table that includes all layers at once.
- Laplacian and eigenvalues: These are math tools that help us understand how things “flow” on the network (like heat, traffic, or opinions). One special number (often called λ₂) tells us how hard it is to break the network apart or how fast things can synchronize.
- Multilayer metrics designed for layers:
- Participation coefficient: Does a node spread its connections across many layers (a true all-rounder) or mostly in one layer (a specialist)?
- Mutually largest connected component (MLCC): The biggest set of nodes that stay connected in every layer at the same time—useful for judging overall system resilience.
- Interlayer correlations: Do nodes popular in one layer tend to be popular in another? This matters for how processes spread or synchronize.
Finding groups (communities)
Communities are groups of nodes more tightly connected to each other than to the rest. In multilayer networks, there are three main ways to find them:
- Flattening: Merge all layers into one and run standard community detection. It’s simple but loses layer details.
- Layer-by-layer: Find communities in each layer, then combine the results (using ideas like consensus or feature fusion).
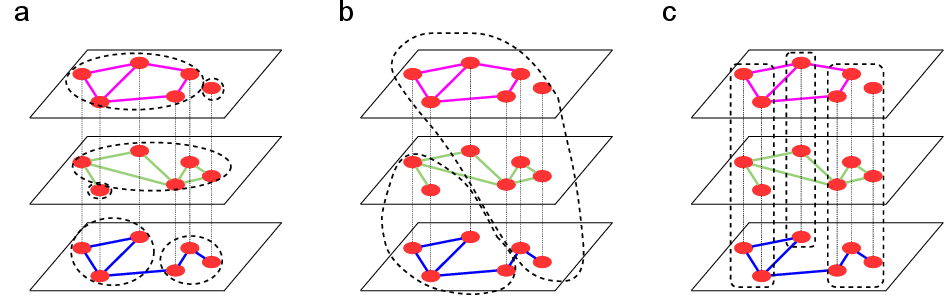
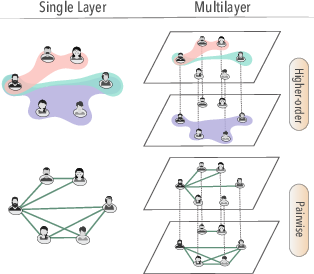
- True multilayer methods: Work on all layers together and detect communities of node-layer pairs (for example, the same person might belong to different groups in different layers). These can find:
- Intralayer communities (within a single layer),
- Cross-layer communities (spanning multiple layers),
- Pillar communities (the same members across layers).
Timing and group interactions
- Temporal networks: When connections change over time, each time-slice can be a layer. Order matters—a path that looks possible in a static picture might be impossible if the timings don’t line up.
- Higher-order interactions: Not all interactions are pair-to-pair. Some involve groups (like group chats or chemical reactions with multiple reactants). Models like hypergraphs capture this. These can show behaviors (like sudden, jumpy transitions) that simple pairwise models miss.
Machine learning tools
The paper also covers methods that turn multilayer networks into vectors (“embeddings”) to help with tasks like predicting future links or uncovering hidden structure. This is handy for large, complex datasets.
What did they find, and why is it important?
From many studies, the paper highlights key lessons:
- Layers matter: Many systems cannot be understood using a single, merged network. Different layers reveal different patterns, and their interactions can create new behaviors.
- Interdependence can be risky: When layers depend on each other (e.g., power grid and internet), failures can cascade quickly and cause abrupt, system-wide breakdowns—unlike the smoother failures seen in single-layer systems.
- Structure shapes dynamics: Interlayer connections can speed up or slow down spreading, synchronization, or consensus. Small changes in how layers connect can have big effects.
- Time changes everything: The order and timing of contacts drastically affect what can spread, who is central, and which routes are possible.
- Groups change outcomes: Higher-order (group) interactions can cause sudden jumps, multiple stable states, or mixed patterns (some parts ordered, some not)—behaviors missed by pair-only models.
- Better detection and inference: New community detection and statistical tools (like multilayer block models) can uncover real groups, link layers, and test if a multilayer view is truly needed.
- Broad applications: The multilayer approach advances understanding in:
- Critical infrastructure and resilience,
- Epidemic spreading and awareness,
- Social behavior and information flow,
- Financial and economic networks,
- Ecology and climate systems,
- Science-of-science (how research fields evolve),
- Medicine (disease-gene-drug networks),
- Neuroscience (different brain connectivity types).
What is the impact of this research?
This review sets the roadmap for the field:
- It gives researchers a shared toolkit and vocabulary to paper complex, layered systems.
- It shows where multilayer models make a practical difference—for example, designing more robust infrastructures, planning better epidemic responses (combining disease and awareness layers), or understanding brain function across different types of connections.
- It calls for community resources: standard datasets, open software, and benchmarks so results are comparable and reproducible.
- It pushes toward the next step: combining time and higher-order interactions and building models that don’t just explain the past but predict what will happen next.
In short, the paper explains how to think in layers—because the world works in layers—and shows how that mindset can lead to smarter decisions, safer systems, and better science.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a consolidated list of the main knowledge gaps, limitations, and open questions that remain unresolved in the paper, stated concretely to guide future research.
- Lack of standardized, open multilayer datasets with ground truth: Curate datasets that include explicit interlayer links/weights, temporal stamps, higher-order interactions, and metadata, with agreed file formats (tensor, supra-adjacency, event graph), and reproducible train/validation/test splits honoring temporal order.
- Absence of rigorous null models and statistical tests for multilayer community detection: Develop multilayer-aware null models that preserve cross-layer correlations and temporal/higher-order structures, along with hypothesis tests to assess the significance of detected communities and mesoscale patterns.
- Limited algorithms for heterogeneous multilayer networks (different node sets per layer): Design community detection, centrality, and spectral methods that no longer assume multiplexity (same nodes across layers), including principled interlayer mappings and constraints.
- Unresolved estimation of interlayer coupling strengths and dependencies from data: Provide statistically consistent estimators (with confidence intervals) for interlayer weights and dependency structures under sampling noise, missing data, and unequal layer coverage.
- Metadata integration beyond post hoc validation: Build probabilistic inference frameworks (e.g., SBMs with covariates) that jointly incorporate node/edge attributes during multilayer community detection and model selection, avoiding label-based validation biases.
- Uncertainty quantification under incomplete and biased data: Create debiasing, imputation, and uncertainty propagation methods for multilayer metrics (e.g., participation coefficient, MLCC), spectral quantities, and inferred communities when layers have uneven sampling.
- Comparative guidance on representations (tensor vs supra-adjacency vs event graph): Establish criteria and benchmarks to determine which representation preserves the dynamics relevant to a target process, and quantify information loss when converting between them.
- General conditions for spectral discontinuities and their dynamical consequences: Extend theory of eigenvalue crossings and abrupt transitions beyond simplified two-layer, undirected cases to weighted, directed, temporal, and higher-order multilayer networks.
- Design and control of interlayer coupling for desired dynamics: Develop optimization algorithms (with cost/robustness constraints) to place or weight interlayer links that maximize synchronizability, accelerate diffusion, or mitigate cascades.
- Predictive (not merely descriptive) multilayer models: Create models that forecast cross-layer dynamics with out-of-sample validation, including causal inference of interventions (e.g., awareness seeding reducing epidemics) and counterfactual analysis.
- Quantifying the “added value” of multilayer over aggregation: Define tests and decision procedures that determine when multilayer modeling is necessary for a given task, and when aggregation suffices without significant loss in accuracy.
- Scalability to massive, high-dimensional systems: Develop subquadratic, streaming, and distributed algorithms (including GPU-enabled) for multilayer community detection, spectral analysis, and dynamical simulations at NL-scale.
- Minimal temporal backbones tailored to a target process: Formalize criteria and efficient algorithms to extract process-specific temporal backbones (e.g., epidemic time-respecting paths), with accuracy–privacy trade-offs and error guarantees.
- Multi-timescale inference in temporal multilayer networks: Provide methods to detect, separate, and model interacting timescales (process vs network evolution), and quantify their impact on thresholds, phase transitions, and metastability.
- Machine learning and embeddings for multilayer/temporal networks: Develop interpretable, cross-layer embeddings that respect constraints (timing, causality, higher-order interactions), with robust train/test protocols and metrics for tasks like link prediction and influence forecasting.
- Canonical operators for higher-order systems: Establish unified, well-posed definitions of adjacency and Laplacians that decouple structure from dynamics in hypergraphs and simplicial complexes, including sensitivity analyses and guidelines for model choice.
- Inference of higher-order interactions from pairwise data: Create scalable, noise-tolerant algorithms to detect group interactions (triads and beyond), validate against ground truth, and quantify uncertainty in inferred higher-order structures.
- Joint multilayer–higher-order modeling: Develop analytical tools (e.g., percolation theory, MSF) and simulation frameworks for systems that combine layered architectures with group interactions, including phase diagrams and control strategies.
- Temporal hypergraphs at scale: Provide algorithms, null models, and process models for evolving group interactions (duration, concurrency), including benchmarks demonstrating when temporal hypergraphs outperform pairwise temporal networks.
- Statistical significance and reproducibility in multilayer community detection: Introduce uncertainty-aware consensus partitions, confidence intervals on assignments, and standardized evaluation metrics for intralayer, cross-layer, and pillar communities.
- Causality across layers: Adapt causal discovery to multilayer temporal data to distinguish correlation from causation (e.g., awareness–epidemic, resource–synchronization), and design empirical interventions to test inferred mechanisms.
- Software and interoperability gaps: Build unified, well-documented APIs and pipelines that support tensors, supra-adjacency, event graphs, and hypergraphs, with standardized outputs, provenance tracking, and cross-domain interoperability.
- Handling directionality, signed/inhibitory couplings, and durations: Extend models and metrics to directed edges, negative interlayer couplings (antagonistic interactions), and interaction durations, and analyze their effects on dynamics and robustness.
- Taxonomy of when multiplexity enhances or inhibits processes: Derive predictive rules linking interlayer structural correlations and topology to dynamical outcomes (e.g., thresholds, prevalence, synchronization ranges), validated across domains.
- Empirical validation of model-predicted phenomena: Design experiments and data collection protocols (e.g., multi-modal neuro/social sensing) to test multiplex-induced behaviors such as explosive synchronization, chimera states, and topology-driven instabilities.
Glossary
- Activity-driven frameworks: A class of generative models for temporal networks in which nodes become active and create contacts without memory. "These models range from memoryless activity-driven frameworks~\cite{perra_activity_2012,starnini_topological_2013} to non-Markovian extensions capturing burstiness and memory effects~\cite{moinet_burstiness_2015}."
- Adjacency tensor: A tensor representation that encodes intralayer and interlayer connections in a multiplex network, preserving layer separation. "A multiplex network can then be represented by an adjacency tensor of order 4 with elements ."
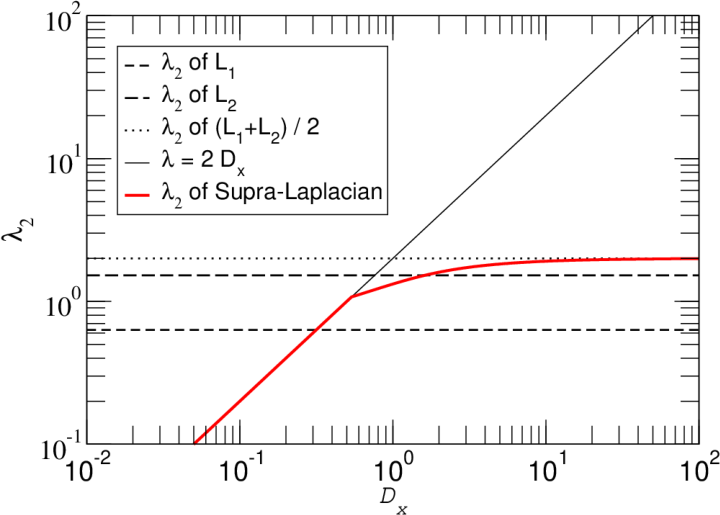
- Algebraic connectivity (Fiedler value): The second-smallest eigenvalue of the Laplacian that measures network cohesiveness and affects dynamics like synchronization. "The algebraic connectivity or Fiedler value~\cite{Fiedler1973}, given by the second-smallest eigenvalue () of the supra-Laplacian matrix, is a key metric."
- Betweenness centrality: A centrality measure quantifying how often a node appears on shortest paths; generalized for multilayer networks. "Some of them are purely topological, such as the eigenvector, the Katz, and the betweenness centralities~\cite{DeDomenico2013, DeDomenico2015ranking, sola2013eigenvector, taylor2021}."
- Burstiness: The tendency of events to cluster in time rather than occurring uniformly, impacting temporal network processes. "new phenomena, such as the burstiness of human interactions, where events are clustered in time rather than occurring randomly~\cite{barabasi2005origin,karsai2018bursty}."
- Cascading failures: Domino-like breakdowns where failures in one layer propagate and cause failures elsewhere. "producing abrupt percolation transitions and cascading failures, phenomena not observed in isolated networks."
- Chimera-like states: Dynamical regimes combining coherent and incoherent activity across network modules. "The interplay between these types of couplings gives rise to chimera-like states, where coherent and incoherent activity coexist across modules."
- Clique percolation method: A community detection technique based on percolation of overlapping cliques, adapted to multilayer settings. "Local exploration methods, like seed set expansion~\cite{interdonato17}, label propagation~\cite{boutemine17} or the clique percolation method~\cite{afsarmanesh18}, as well as random walk-based algorithms such as Infomap~\cite{dedomenico15} and Walktrap~\cite{kuncheva15}, have also been adapted."
- Consensus partition: An aggregated community assignment that best matches multiple input partitions. "one could derive a consensus partition, which is the division that is closest to all the input ones, on average~\cite{strehl02}."
- Degree assortativity: A correlation pattern describing whether high-degree nodes tend to connect to other high-degree nodes. "Beyond intralayer patterns like degree assortativity (whether high-degree nodes connect to other high-degree nodes~\cite{pastor01b,newman02}), we can measure interlayer correlations."
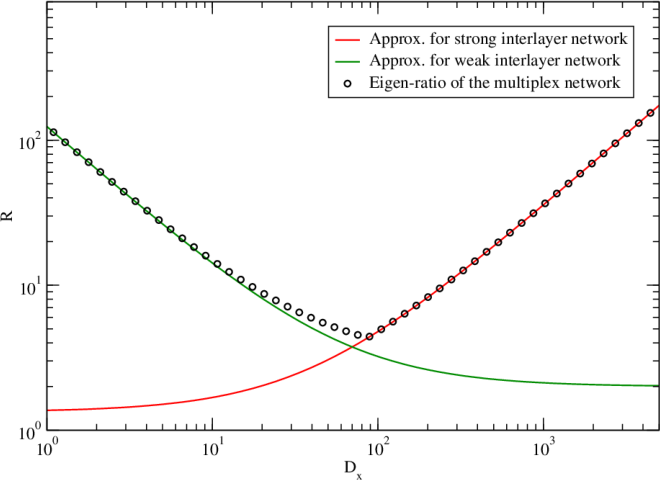
- Eigenratio: The ratio of the largest to the second-smallest Laplacian eigenvalues, used to assess synchronizability. "The synchronizability of a network can be assessed by the eigenratio R = \frac{\lambda_N}{\lambda_2},"
- Eigenvector centrality: A centrality measure where a node’s importance depends on the importance of its neighbors, extended to multilayer networks. "Some of them are purely topological, such as the eigenvector, the Katz, and the betweenness centralities~\cite{DeDomenico2013, DeDomenico2015ranking, sola2013eigenvector, taylor2021}."
- Event graph: A representation where interactions themselves are nodes, linked by temporal adjacency. "The event graph, in contrast, treats interactions themselves as nodes, linking temporally adjacent events involving shared participants~\cite{kivela2018mapping}."
- Explosive synchronization: An abrupt transition to synchrony induced by interlayer feedback or structural features. "This mutual feedback leads to the spontaneous emergence of explosive synchronization and highly heterogeneous resource distributions."
- Hawkes: A point-process model capturing self-exciting temporal dynamics used as a generative mechanism for time-stamped interactions. "models based on Hawkes or other dynamical processes"
- Hypergraphs: Higher-order network models where hyperedges can connect more than two nodes, capturing group interactions. "Mathematically, higher-order interactions are usually modelled using hypergraphs or simplicial complexes~\cite{Battiston2020,Boccaletti2023,Torres2021}."
- Infomap: A community detection algorithm based on random walks and information compression, adapted for multilayer networks. "Local exploration methods, like seed set expansion~\cite{interdonato17}, label propagation~\cite{boutemine17} or the clique percolation method~\cite{afsarmanesh18}, as well as random walk-based algorithms such as Infomap~\cite{dedomenico15} and Walktrap~\cite{kuncheva15}, have also been adapted."
- Interdependent networks: Multilayer systems where nodes in one layer depend functionally on nodes in another, altering robustness and dynamics. "A major turning point came with the study of interdependent networks, where nodes in one layer depend on nodes in another layer for functionality~\cite{buldyrev_2010,Vespignani2010Apr}."
- Interlayer mutual information: An information-theoretic measure of redundancy or similarity between layers’ connectivity patterns. "This can be done by calculating the interlayer mutual information or other correlation measures between the adjacency matrices of different layers."
- Katz centrality: A centrality measure that sums paths of all lengths with attenuation, generalized for multilayer networks. "Some of them are purely topological, such as the eigenvector, the Katz, and the betweenness centralities~\cite{DeDomenico2013, DeDomenico2015ranking, sola2013eigenvector, taylor2021}."
- Kuramoto phase oscillator: A canonical nonlinear oscillator model used to study synchronization on networks. "In networks where each node represents a Kuramoto phase oscillator, determines the timescale for convergence to the synchronized state~\cite{Almendral2007}."
- Label propagation: A fast, heuristic community detection method that spreads labels through the network. "Local exploration methods, like seed set expansion~\cite{interdonato17}, label propagation~\cite{boutemine17} or the clique percolation method~\cite{afsarmanesh18}, as well as random walk-based algorithms such as Infomap~\cite{dedomenico15} and Walktrap~\cite{kuncheva15}, have also been adapted."
- Master Stability Function (MSF): A framework that reduces synchronization stability analysis to the eigenvalues of coupling matrices. "The stability of the synchronized state in these systems can be analyzed using the Master Stability Function (MSF) formalism~\cite{pecora98},"
- Modularity maximization: A community detection approach extended with multilayer null models to handle interlinks and intralinks. "Modularity maximization was generalized by defining a multilayer null model based on random walks, with intralinks and interlinks playing different roles~\cite{mucha10}."
- Multiplex network: A multilayer network where the same node exists across layers and interlayer links connect node replicas. "A multiplex network is a specific and widely used type of multilayer network where nodes represent the same entity on every layer, and interlayer links only connect a node to itself across different layers."
- Mutually largest connected component (MLCC): The largest set of nodes connected within each and every layer simultaneously. "Another network-level metric with no single-layer equivalent is the mutually largest connected component (MLCC)."
- Non-Markovian extensions: Temporal models that incorporate memory effects and burstiness beyond the memoryless assumption. "to non-Markovian extensions capturing burstiness and memory effects~\cite{moinet_burstiness_2015}."
- PageRank: A random-walk-based centrality measure, generalized to multilayer contexts. "Notable examples include PageRank~\cite{halu2013multiplex}"
- Participation coefficient: A metric that quantifies how evenly a node’s connections are distributed across layers. "For instance, the participation coefficient measures how evenly a node's links are spread across the different layers."
- Percolation transitions: Structural phase transitions in connectivity, which can be abrupt in interdependent systems. "producing abrupt percolation transitions and cascading failures, phenomena not observed in isolated networks."
- Pillar communities: A constrained multilayer community type where all replicas of a node across layers belong to the same community. "Pillar communities are a constrained type where if a node belongs to a community, all of its counterparts in other layers also belong to the same community."
- Random walk occupation probability: A centrality defined by the steady-state probability that a random walker occupies a node. "Notable examples include PageRank~\cite{halu2013multiplex} or a centrality related to the random walk occupation probability~\cite{sole2016random}, among others."
- Reaction-diffusion systems: Dynamical systems where entities diffuse and react, exhibiting new instabilities on multiplex networks. "A paradigmatic case in which multiplexity alters the behaviour of a well-understood process is that of reaction-diffusion systems."
- Relay layer: An intermediary layer that mediates synchronization between layers that are not directly connected. "Another work examined how two layers not directly connected can synchronize through the mediation of a central relay layer~\cite{Leyva2018}."
- Seed set expansion: A local community detection strategy that grows communities from seed nodes. "Local exploration methods, like seed set expansion~\cite{interdonato17}, label propagation~\cite{boutemine17} or the clique percolation method~\cite{afsarmanesh18}, as well as random walk-based algorithms such as Infomap~\cite{dedomenico15} and Walktrap~\cite{kuncheva15}, have also been adapted."
- Simplicial complexes: Higher-order structures where, unlike general hypergraphs, all subsets of a group interaction are present. "Mathematically, higher-order interactions are usually modelled using hypergraphs or simplicial complexes~\cite{Battiston2020,Boccaletti2023,Torres2021}."
- Stochastic block model (SBM): A probabilistic generative model used for community detection and layer inference in multilayer networks. "Furthermore, statistical inference methods, primarily based on the stochastic block model (SBM), offer a principled framework to detect communities, infer relationships between layers, and even test whether an observed single-layer network is better explained as an aggregation of hidden layers~\cite{peixoto15,debacco17}."
- Supra-adjacency matrix: A block matrix representing the entire multiplex as a single large graph, with intralayer and interlayer blocks. "the supra-adjacency matrix is a block matrix."
- Supra-adjacency representation: A multilayer encoding for temporal networks where node-time pairs become nodes linked by observed interactions. "The supra-adjacency representation encodes node-time pairs as nodes in a multilayer structure, linking them according to the observed interactions~\cite{valdano2015analytical,sato2019dyane}."
- Supra-Laplacian: The Laplacian constructed from the supra-adjacency matrix, linking structure to dynamics across layers. "Similarly, the supra-Laplacian matrix can be constructed from the supra-adjacency matrix ~\cite{kivela14, gomez2013}."
- Temporal backbones: Filtered subgraphs highlighting interaction pairs that are statistically significant over time. "At the local scale, temporal backbones highlight node pairs whose interaction frequencies significantly exceed what would be expected under a temporal null model~\cite{kobayashi2019structured}."
- Temporal cores: Dense time-localized substructures identified by extending core decomposition to temporal windows. "temporal cores generalize the static core decomposition to uncover dense substructures active over defined time windows~\cite{galimberti2018mining}."
- Temporal motifs: Frequently recurring, time-ordered patterns of interactions in temporal networks. "Temporal motifs identify frequently recurring, time-ordered subgraphs~\cite{kovanen2013temporal},"
- Temporal networks: Networks with time-resolved interactions, often represented as sequences of snapshots. "A temporal network can be represented as a sequence of static snapshots, which naturally fits the multilayer network framework where each layer is a snapshot in time."
- Temporal paths: Time-respecting sequences of interactions that constrain the flow of information or contagion. "Researchers recognized that information flows along temporal paths, which are a set of time-respecting sequences of interactions~\cite{kempe2000connectivity,holme2005network}."
- Temporal rich-club coefficient: A measure of whether highly connected nodes form persistent, simultaneous ties over time. "Similarly, the temporal rich-club coefficient measures whether highly connected nodes in the aggregate network tend to form simultaneous, persistent connections~\cite{pedreschi2022temporal}."
- Tensor formalism: A representation framework that models multilayer networks with tensors to explicitly preserve layer distinctions. "Second, we have the formalism based on the supra-adjacency matrix, which represents the entire multilayer system as a single, larger network." [Note: preceding sentence] "First, we have the tensor formalism, in which the separation of layers can be maintained explicitly."
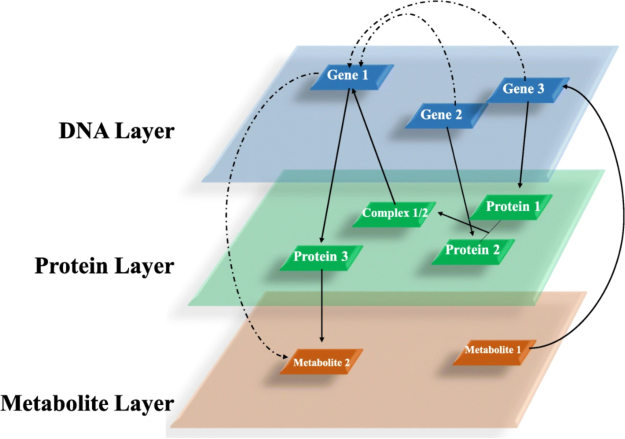
- Triadic percolation: Percolation processes defined over group (triad) interactions in higher-order or multilayer settings. "Recent work has begun to explore multilayer extensions of higher-order systems (Fig.~\ref{fig:hypergraph}), such as triadic percolation processes and interdependent dynamics across layers~\cite{Sun2023,Chang2023}."
- Turing-like pattern formation: Spatial pattern formation driven by reaction-diffusion dynamics, enabled by interlayer coupling. "Remarkably, the presence of interlayer coupling allows for Turing-like pattern formation even when both species have identical mobility ratesâsomething impossible in single-layer networks."
- Walktrap: A community detection algorithm based on random walks that has been adapted to multilayer networks. "Local exploration methods, like seed set expansion~\cite{interdonato17}, label propagation~\cite{boutemine17} or the clique percolation method~\cite{afsarmanesh18}, as well as random walk-based algorithms such as Infomap~\cite{dedomenico15} and Walktrap~\cite{kuncheva15}, have also been adapted."
Practical Applications
Immediate Applications
The following items are deployable with existing data, methods, and computational tooling outlined in the paper. Each bullet notes sectors, concrete use cases, enabling tools/workflows, and key assumptions/dependencies impacting feasibility.
- Critical infrastructure resilience assessment and planning
- Sectors: energy, telecommunications, transportation, water
- Use case: quantify robustness and identify weak points in interdependent systems (e.g., power grid–ICT coupling), prioritize redundancy and backup placement, and plan islanding strategies.
- Tools/workflows: build a supra-adjacency from asset registries; compute spectral indicators (λ₂, eigenratio R) and MLCC; run percolation/cascade simulations; use Master Stability Function (MSF) to tune coupling.
- Assumptions/dependencies: accurate multi-layer topology and interlayer mappings; availability of failure propagation models; stationarity or known coupling ranges; cross-operator data sharing.
- Cascading failure tabletop drills and contingency design
- Sectors: emergency management, utilities, public safety
- Use case: simulate plausible failure chains across layers to inform drills and response protocols; rank assets by multilayer centrality and participation coefficient to prioritize protection.
- Tools/workflows: multiplex percolation stress tests; layer-specific community detection; scenario generation via SBM-inferred mesoscale structure.
- Assumptions/dependencies: validated interdependence rules; access to detailed infrastructure inventories; scenario calibration with historical incidents.
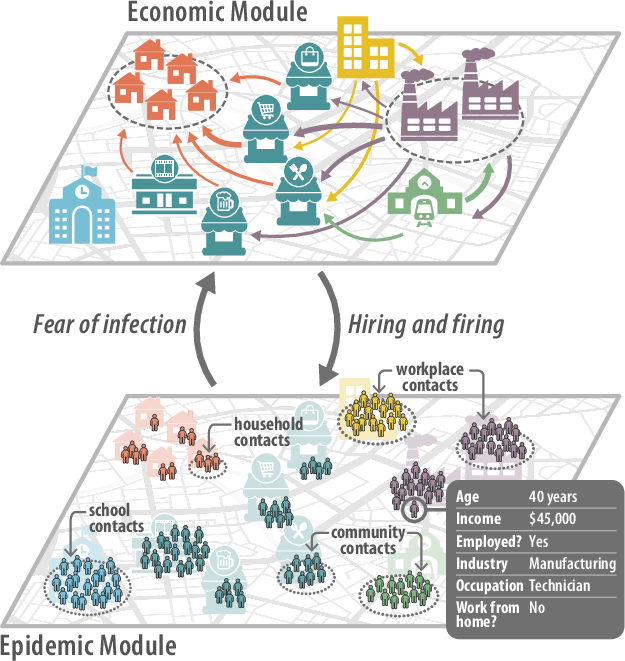
- Epidemic–awareness co-diffusion strategy design
- Sectors: healthcare, public health policy, social platforms
- Use case: design targeted health messaging campaigns that inhibit disease spread by leveraging the awareness layer; adjust thresholds to reduce prevalence based on cross-layer feedback.
- Tools/workflows: two-layer SIR/SEIR models coupled to an information diffusion layer; threshold and parameter sweeps; temporal event-graph contact modeling for micro-targeting.
- Assumptions/dependencies: high-resolution contact data and reliable social media diffusion signals; behavioral inhibition effects are correctly modeled; privacy and consent frameworks.
- Hospital infection control via temporal backbones
- Sectors: healthcare
- Use case: identify time-respecting transmission paths and high-risk wards/shifts; redesign rotas and cleaning schedules; adjust cohorting and room assignments.
- Tools/workflows: temporal networks from sensor data; event graphs; temporal motif and backbone extraction; time-respecting centrality for intervention targeting.
- Assumptions/dependencies: wearable sensor or EHR-derived proximity data; privacy-preserving pipelines; buy-in from clinical operations.
- Cross-platform misinformation monitoring and moderation
- Sectors: software/platforms, public policy, media
- Use case: track communities bridging platforms; identify cross-layer influencers using participation coefficient; prioritize interventions on multi-active accounts.
- Tools/workflows: multilayer Infomap or SBM; interlayer similarity/redundancy measures; embedding-based anomaly detection.
- Assumptions/dependencies: platform data access and interoperability; robust identity linkage across layers; moderation policy constraints.
- Marketing and customer segmentation across channels
- Sectors: retail, fintech, digital advertising
- Use case: detect cross-market segments and multi-channel communities; tailor offers to pillar communities and cross-layer clusters.
- Tools/workflows: feature/partition integration; multilayer community detection; node embeddings for link prediction and next-best-offer.
- Assumptions/dependencies: unified customer IDs; consented multi-source data; stable segment behavior across layers.
- Supply chain risk monitoring in interdependent networks
- Sectors: manufacturing, logistics
- Use case: integrate supplier–customer–finance–logistics layers; identify bottlenecks and critical brokers; stress-test for shocks and reroute contingencies.
- Tools/workflows: supra-adjacency construction; MLCC size sensitivity; interlayer assortativity/correlation analysis; embedding-based risk scoring.
- Assumptions/dependencies: multi-party data sharing; standardized ontologies; up-to-date transactional feeds.
- Financial systemic risk stress testing
- Sectors: finance, central banking, regulation
- Use case: model contagion across interbank, derivatives, cross-holdings layers; assess thresholds for abrupt transitions; inform macroprudential buffers.
- Tools/workflows: multilayer SBM inference; percolation/cascade simulations; layer-synchronized stress scenarios.
- Assumptions/dependencies: regulatory access to exposures; timely, granular data; policy frameworks for scenario deployment.
- Multimodal transportation scheduling and optimization
- Sectors: transportation, urban planning
- Use case: analyze time-respecting routes across public transit, micro-mobility, and road networks; identify temporal motifs causing congestion; redesign schedules for synchrony.
- Tools/workflows: temporal multilayer network modeling; event-graph path analysis; motif-based rescheduling.
- Assumptions/dependencies: timestamped GTFS/traffic feeds; reliable interlayer transfer data; operational flexibility.
- Brain network analysis and synchronization control
- Sectors: neuroscience, neuroengineering
- Use case: characterize multi-modal connectivity (EEG/fMRI/DTI) and control synchronization regimes; detect chimera states; assess resource–synchrony feedback.
- Tools/workflows: multiplex Kuramoto models; MSF-based stability ranges; relay-mediated synchronization analysis.
- Assumptions/dependencies: accurate modality alignment; individualized parameter calibration; clinical interpretability.
- Drug repurposing and patient stratification via network medicine
- Sectors: pharma, precision medicine
- Use case: detect disease modules across multi-omics layers; predict drug–disease links; stratify patients by multilayer centrality and community membership.
- Tools/workflows: multilayer community detection (SBM); embeddings for link prediction; cross-layer similarity to validate targets.
- Assumptions/dependencies: curated, interoperable omics and phenotype datasets; rigorous validation (in vitro/in vivo); regulatory pathways.
- Climate teleconnection monitoring and early warnings
- Sectors: energy planning, agriculture, policy
- Use case: track temporal climate networks across variables (pressure, temperature, precipitation) to flag regime shifts; support seasonal planning.
- Tools/workflows: snapshot similarity clustering; temporal motifs and autocorrelation; backbone extraction for actionable signals.
- Assumptions/dependencies: high-quality reanalysis/remote-sensing data; domain-calibrated thresholds; caution about causality.
- Campus-level public health and timetable optimization
- Sectors: education
- Use case: reduce transmission risk by re-timing classes/cohorts based on temporal rich-club and core analysis; instrument contact-respecting intervention design.
- Tools/workflows: temporal core decomposition; time-respecting path mapping; scenario testing.
- Assumptions/dependencies: sensor or Wi-Fi-derived proximity logs; stakeholder buy-in; privacy safeguards.
Long-Term Applications
The following items are strategically promising but require further research, scaling, data standardization, or development before broad deployment.
- Real-time predictive digital twins of interdependent infrastructures
- Sectors: energy, transportation, smart cities
- Use case: continuously simulate cross-layer dynamics and control (e.g., frequency regulation tied to ICT states), enabling anticipatory mitigation of cascades.
- Tools/workflows: integrated temporal multilayer models; MSF-guided controllers; streaming data assimilation.
- Assumptions/dependencies: standardized datasets/software; low-latency telemetry; robust model calibration; cross-operator governance.
- Hypergraph–multiplex contagion management for group exposures
- Sectors: public health, workplace safety, events
- Use case: model and mitigate discontinuous transitions and multistability in group-based transmission (e.g., classrooms, meetings) across venue layers.
- Tools/workflows: temporal hypergraphs; triadic percolation; higher-order threshold models; intervention optimization.
- Assumptions/dependencies: reliable capture of group interactions; tractable calibration; policy mechanisms for adaptive interventions.
- Macroprudential regulation grounded in multilayer systemic risk metrics
- Sectors: finance, policy
- Use case: codify stress test standards using MLCC, interlayer assortativity/correlation, and abrupt transition diagnostics; mandate cross-layer disclosures.
- Tools/workflows: regulatory dashboards; standardized reporting; scenario libraries.
- Assumptions/dependencies: legal authority; global harmonization; confidentiality management.
- Privacy-preserving temporal backbone extraction and data sharing
- Sectors: healthcare, platforms, mobility
- Use case: share minimal, process-relevant network backbones for research and operations without full raw data disclosure.
- Tools/workflows: null-model filtering; differential privacy atop event-graph representations; federated analysis.
- Assumptions/dependencies: accepted privacy standards; provable utility guarantees; stakeholder incentives.
- Personalized digital wellbeing assistants via multiplex embeddings
- Sectors: consumer software, mental health
- Use case: detect harmful cross-platform information flows, nudge consumption patterns, and dampen cascade risks.
- Tools/workflows: user-level multilayer embeddings; participation coefficient–based alerts; on-device inference.
- Assumptions/dependencies: user consent and transparency; model robustness; ethical safeguards.
- Neuromodulation therapies informed by multiplex synchronization regimes
- Sectors: healthcare, medical devices
- Use case: tailor stimulation protocols to exploit chimera states and relay synchronization; manage transitions between resting and task-related activity.
- Tools/workflows: patient-specific multiplex models; closed-loop control; clinical trial pipelines.
- Assumptions/dependencies: high-quality multi-modal data; safety and efficacy trials; regulatory approval.
- Integrated ecological–climate management and early warning systems
- Sectors: conservation, agriculture, insurance
- Use case: link food webs and habitat networks with climate layers to predict tipping points; guide adaptive resource management.
- Tools/workflows: multilayer ecological networks; temporal teleconnection analysis; scenario planning.
- Assumptions/dependencies: sustained monitoring; cross-disciplinary calibration; uncertainty quantification.
- Autonomous grid control via spectral optimization
- Sectors: energy
- Use case: design controllers that optimize eigenratio R across layers to maintain synchrony under disturbances; dynamic coupling reconfiguration.
- Tools/workflows: spectral control policies; digital twin integration; fast optimization solvers.
- Assumptions/dependencies: advanced sensing and actuation; cyber-physical security; regulatory frameworks.
- Standardized software stacks and benchmarks for multilayer/higher-order analytics
- Sectors: software, academia
- Use case: reproducible pipelines for community detection, temporal motifs, hypergraph Laplacians, and embeddings; shared datasets for model evaluation.
- Tools/workflows: open-source libraries; data schemas; automated validation harnesses.
- Assumptions/dependencies: community consensus; funding; long-term maintenance.
- Urban epidemic–mobility digital twin
- Sectors: policy, urban planning
- Use case: integrate contact networks with transit layers to co-optimize public health and mobility; simulate interventions (masking, timetabling, routing).
- Tools/workflows: event-graph modeling; co-diffusion dynamics; multi-objective optimization.
- Assumptions/dependencies: rich IoT data; interagency collaboration; social acceptance.
- Cross-layer cybersecurity risk simulation
- Sectors: cybersecurity, critical infrastructure
- Use case: simulate attacks propagating across ICT–OT–physical layers; identify demultiplexing strategies to isolate impacts.
- Tools/workflows: multiplex percolation with attack vectors; relay-layer analysis; resilience playbooks.
- Assumptions/dependencies: detailed OT/ICT maps; sensitive data access; adversarial modeling.
- Science-of-science decision support for funding portfolios
- Sectors: research policy, funding agencies
- Use case: model knowledge diffusion across fields and collaboration layers to optimize portfolios and anticipate emerging domains.
- Tools/workflows: multilayer SBM inference; temporal embedding of co-authorship/citation networks; scenario analysis.
- Assumptions/dependencies: comprehensive bibliometric data; policy alignment; fairness and bias audits.
Collections
Sign up for free to add this paper to one or more collections.