Visualizing LLM Latent Space Geometry Through Dimensionality Reduction (2511.21594v1)

Abstract: LLMs achieve state-of-the-art results across many natural language tasks, but their internal mechanisms remain difficult to interpret. In this work, we extract, process, and visualize latent state geometries in Transformer-based LLMs through dimensionality reduction. We capture layerwise activations at multiple points within Transformer blocks and enable systematic analysis through Principal Component Analysis (PCA) and Uniform Manifold Approximation (UMAP). We demonstrate experiments on GPT-2 and LLaMa models, where we uncover interesting geometric patterns in latent space. Notably, we identify a clear separation between attention and MLP component outputs across intermediate layers, a pattern not documented in prior work to our knowledge. We also characterize the high norm of latent states at the initial sequence position and visualize the layerwise evolution of latent states. Additionally, we demonstrate the high-dimensional helical structure of GPT-2's positional embeddings, the sequence-wise geometric patterns in LLaMa, and experiment with repeating token sequences. We aim to support systematic analysis of Transformer internals with the goal of enabling further reproducible interpretability research. We make our code available at https://github.com/Vainateya/Feature_Geometry_Visualization.

• The paper demonstrates a systematic pipeline using PCA and UMAP to reveal latent space geometry in transformer models.
• It finds a distinct separation between attention and MLP representations, supporting component disentanglement.
• The study shows that positional encoding differences in GPT-2 and LLaMa significantly affect latent state patterns.

Visualizing LLM Latent Space Geometry Through Dimensionality Reduction

Introduction

The paper "Visualizing LLM Latent Space Geometry Through Dimensionality Reduction" (2511.21594) systematically investigates the geometry of latent state representations in Transformer-based LLMs. It analyzes internal activations of both GPT-2 and LLaMa by capturing layerwise representations and employing PCA and UMAP for dimensionality reduction. The objective is twofold: to expose interpretable geometric patterns underpinning feature organization and to delineate differences in how attention and MLP pathways—core elements of the Transformer—encode and manipulate internal representations. The methodology and results contribute to mechanistic interpretability, providing reproducible frameworks to probe LLM internals.

Transformer Architectural Perspectives

The paper adopts the residual stream-centric view of Transformer architectures, emphasizing the shared communication channel induced by skip connections. Rather than treating the model as a strict depth-wise sequence, this perspective highlights the additive, compositional nature of component outputs, underscoring the collaborative organization of feature subspaces. This unifies the analysis of various architectural elements—token embedding, multi-head attention, MLP, normalization, and unembedding layers—within a single representational geometry.

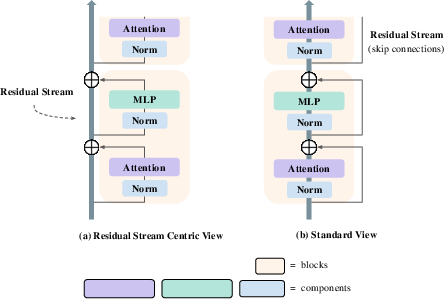
Figure 1: The standard sequential and residual stream-centric perspectives of Transformer architectures are mathematically equivalent but facilitate different analytical decompositions.

Methodology: Latent State Capture and Visualization Pipeline

The authors design a robust three-stage pipeline: (1) extracting activations (latent states) across multiple well-defined capture points within every Transformer block, (2) organizing latent representations together with metadata, and (3) applying dimensionality reduction (PCA and UMAP) for low-dimensional visualization. Capture locations reflect key architectural operations: pre- and post-normalization, attention, MLP, and post-residual addition activations. Modes include "text" (full sequence sampled from datasets) and "singular" (isolated token probing).

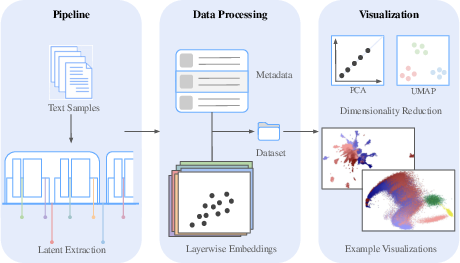
Figure 2: Schematic overview of the latent state extraction, metadata structuring, and dimensionality reduction pipeline.

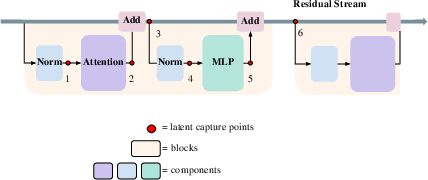
Figure 3: The six capture points per Transformer block, enabling isolation of normalization, attention, and MLP activations, both before and after residual addition.

Layerwise Norm Dynamics and Position Dependence

Systematic analysis of latent state norms across layers and sequence positions reveals several phenomena:

• The initial (0-th) sequence position consistently yields activations with significantly higher norm, in both GPT-2 and LLaMa, regardless of token identity. These high-norm states are robust to architecture details—emerging despite LLaMa's use of relative positional encoding (RoPE) and not only with the <BOS> token.
• Maximum activation norm is not concentrated in early or late layers, but appears in intermediate blocks, subsequently suppressed towards output.

This has direct implications for interpretability and preprocessing: outlier-norm activations dominate low-dimensional projections, potentially obscuring nuanced geometry unless properly handled.

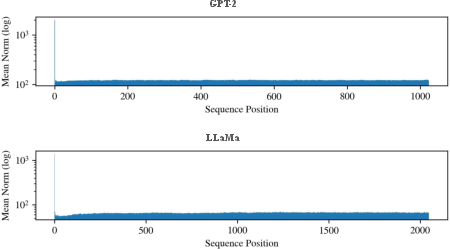
Figure 4: Norm trajectories of latent states from intermediate layers across sequence positions, demonstrating pronounced spikes at the 0-th token for both models.

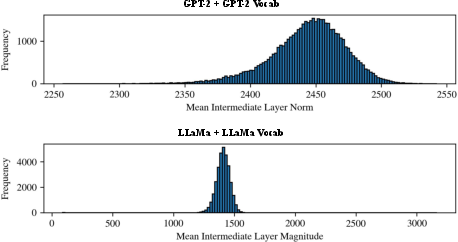
Figure 5: Histogram of intermediate layer latent state norms for all vocabulary tokens input as the initial token, confirming high-norm behavior is ubiquitous.

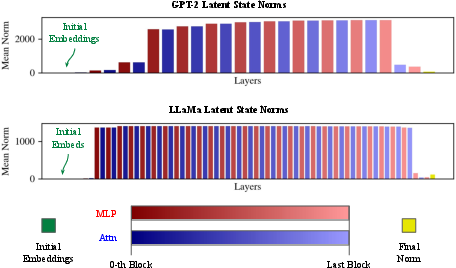
Figure 6: Norm profile of all tokens, stratified by layer index for each model; maximum norms occur in intermediate layers.

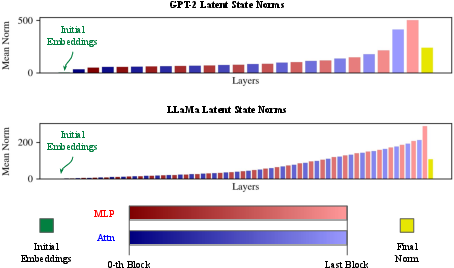
Figure 7: Aggregated layerwise norm progression across all sequence positions (initial token excluded), revealing consistent architectural patterns.

Layerwise Geometry and Principal Component Structure

When projecting unit-normalized latent states with PCA, clear layerwise progressions emerge in both models, though the structure differs by the nature of positional encoding:

• In GPT-2, strong helical or oscillatory structure is apparent, reflecting the impact of learned positional embeddings.
• In LLaMa, distinct geometric patterns are less pronounced, attesting to the complex effects of RoPE positional encodings.

Sample averaging along sequence or instance dimensions further reveals that variability is captured both by position and by layerwise transformation.

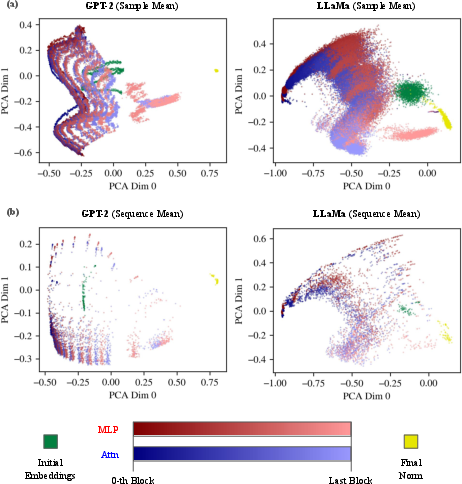
Figure 8: PCA projections of layerwise latent state geometry in GPT-2 and LLaMa; panel (a) averages across samples, panel (b) across sequence positions.

Separation of Attention and MLP Outputs

A key result is the discovery of a persistent separation in the geometric support of pre-add activations from attention and MLP components across intermediate layers. This holds under both PCA and UMAP analysis, regardless of model or probe strategy (unit or raw vectors). Notably, attention-derived representations (blue) and MLP outputs (red) inhabit distinct regions in the low-dimensional embedding space.

This observation suggests that attention and feedforward submodules do not simply conspire within the same representational directions but contribute orthogonally to transformation geometry, supporting decomposability hypotheses. To the authors' knowledge, this separation was previously undocumented.

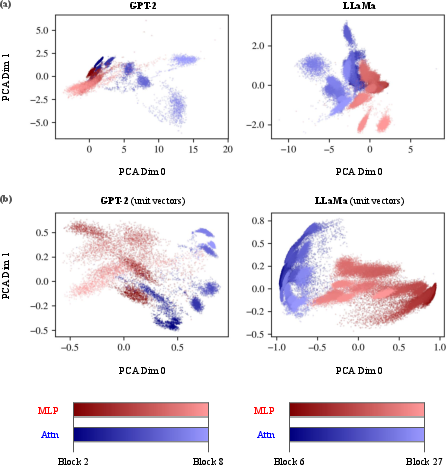
Figure 9: PCA visualizations of pre-add activations, demonstrating clear separation between attention and MLP output geometry.

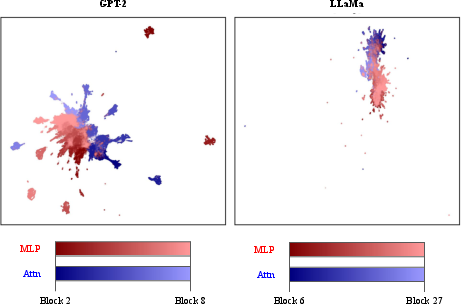
Figure 10: UMAP projections confirm distinct clustering of attention and MLP activations independent of PCA's linearity constraints (cosine metric).

Effects of Sequence Position: Absolute vs. Relative Encoding

Position-dependent geometric signatures are dissected via PCA projections of post-add latent states:

• GPT-2: Positional embeddings induce a high-dimensional helix, visible in projections across all principal component pairs.
• LLaMa: RoPE produces a low-dimensional transition ("tail") in initial positions, converging into an amorphous dense region for later tokens. Structure dissipates quickly in higher PC pairs, indicating lower-dimensionality of sequence effects.

These patterns, especially for LLaMa, highlight the interplay between architecture and representational geometry, and raise open questions about how sequence length and token repetition modulate internal state organization.

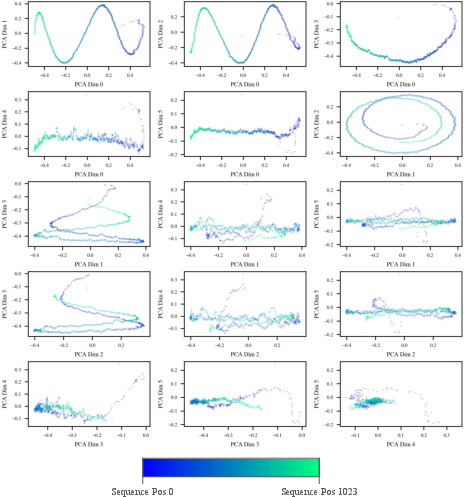
Figure 11: Post-add latent state PCA projections for GPT-2 reveal high-dimensional helical structure tied to learned position embedding.

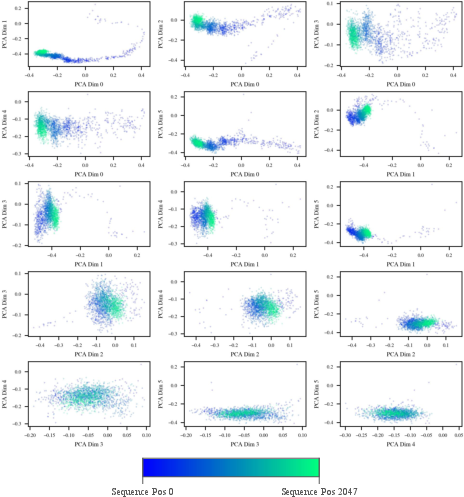
Figure 12: For LLaMa, position-dependent structure is confined to early sequence tokens; later tokens merge in latent space, reflecting RoPE’s design.

Dynamics Under Repeating Token Inputs

A repeating token experiment on LLaMa (with "e") demonstrates a convergence phenomenon:

• Initially, intermediate layer norms are modest, but after $\sim$100 repetitions, later sequence positions' norms sharply increase.
• The final latent vectors for these positions are geometrically similar to the initial <BOS> token state.

This indicates that the model, under RoPE mechanisms, converges to a nearly position-independent representation for large $t$ (except for the outlier initial token). This resonates with prior findings on the constancy of massive activations.

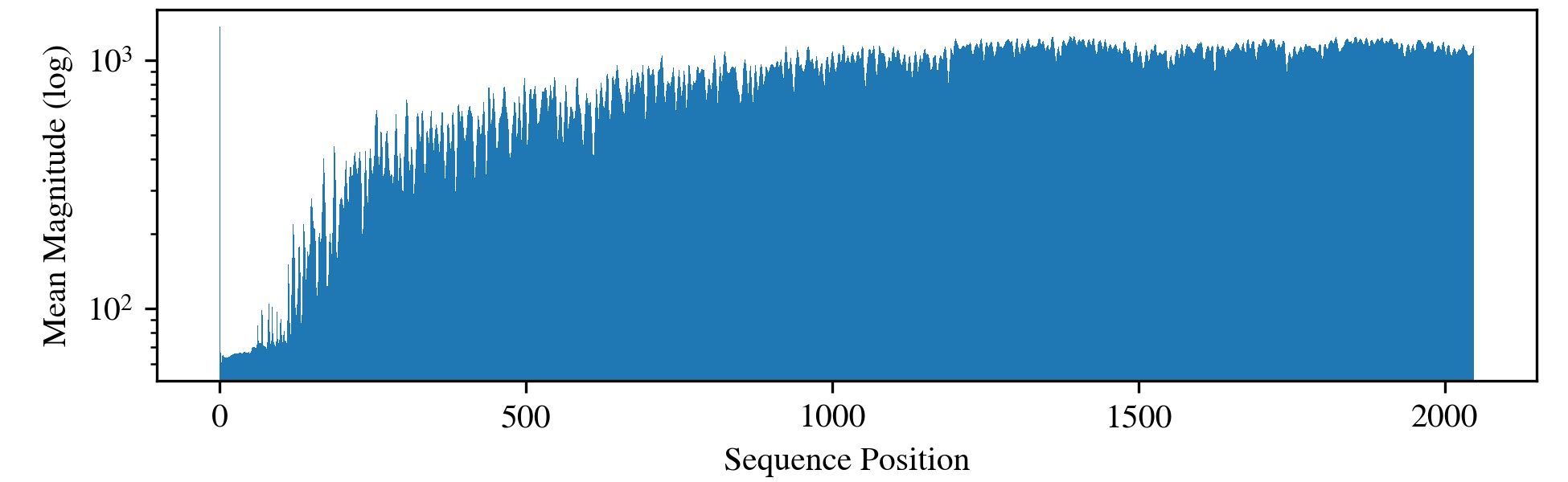
Figure 13: Norm progression across repeated "e" tokens, showing initial moderation followed by a sharp increase.

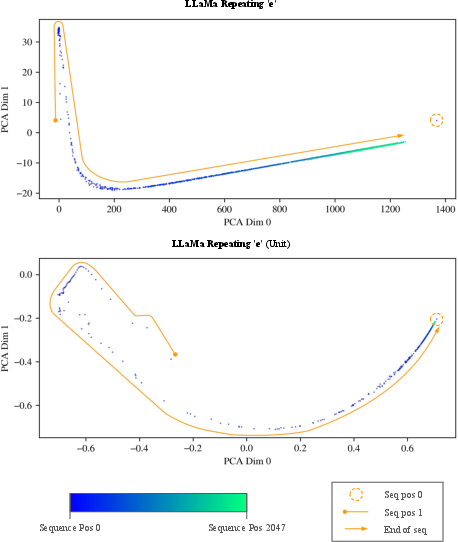
Figure 14: PCA projections reveal latent vector convergence for long repeats; initial position occupies a similar region as terminal tokens.

Implications and Future Directions

These results have both practical and theoretical implications for LLM interpretability:

• Component disentanglement: The distinct separation of attention and MLP representations supports strategies for targeted intervention or ablation (e.g., monosemantic dictionary learning) and justifies the use of component-specific probes in future mechanistic studies.
• Norm-based anomalies: Recognition and removal of initial token artifacts are essential for clean, interpretable low-dimensional analysis.
• Architectural generalization: Relative position encoding architectures (RoPE) induce qualitatively distinct geometric signatures from learned embedding models, indicating that interpretability results may not neatly transfer across LLM families.
• Scaling and invariance: Repeating token convergence suggests that large-scale models may develop position-invariant subspaces in the limit, with implications for context window design and extrapolative robustness.

Prospective work should further quantify the extent and functional implications of component separation, as well as tracing how geometric observables correlate with emergent behaviors such as factual recall, in-context learning, and failure modes.

Conclusion

The systematic layerwise and componentwise visualization of latent state geometry in LLMs offers concrete insight into representational structure and transformation dynamics. In particular, the demonstrated separation between attention and MLP activations, and the nuanced effects of position encoding, invite deeper theoretical analysis and form a productive basis for developing scalable interpretability tools. The provided pipeline and codebase are likely to facilitate robust, reproducible interpretability research and support the ongoing formalization of feature geometry in large models.