Deep Learning as a Convex Paradigm of Computation: Minimizing Circuit Size with ResNets (2511.20888v1)

Abstract: This paper argues that DNNs implement a computational Occam's razor -- finding the simplest' algorithm that fits the data -- and that this could explain their incredible and wide-ranging success over more traditional statistical methods. We start with the discovery that the set of real-valued function $f$ that can be $ε$-approximated with a binary circuit of size at most $cε^{-γ}$ becomes convex in theHarder than Monte Carlo' (HTMC) regime, when $γ>2$, allowing for the definition of a HTMC norm on functions. In parallel one can define a complexity measure on the parameters of a ResNets (a weighted $\ell_1$ norm of the parameters), which induce a `ResNet norm' on functions. The HTMC and ResNet norms can then be related by an almost matching sandwich bound. Thus minimizing this ResNet norm is equivalent to finding a circuit that fits the data with an almost minimal number of nodes (within a power of 2 of being optimal). ResNets thus appear as an alternative model for computation of real functions, better adapted to the HTMC regime and its convexity.

• The paper establishes a convex framework connecting HTMC norms and ResNet parameter norms to approximate minimal circuit size for real-valued functions.
• It introduces the HTMC norm and a corresponding ResNet norm, providing quantitative sandwich bounds that relate continuous function complexity with circuit size minimization.
• The analysis yields PAC generalization bounds and suggests new optimization pathways for designing efficient deep learning models in high dimensions.

Deep Learning as Convex Computation: The Circuit Size Minimization Perspective for ResNets

Introduction and Motivation

This work presents a rigorous framework bridging circuit complexity and deep learning, specifically analyzing Residual Networks (ResNets) as computational models that effectively approximate minimal-size circuits for real-valued functions. Motivated by the longstanding difficulty of the minimal circuit size problem (MCSP)—which is NP and conjectured to be NP-complete—this paper identifies a function complexity regime, the Harder than Monte Carlo (HTMC) regime, in which the set of $\epsilon$-approximable functions by circuits of size $O(\epsilon^{-\gamma})$ becomes (essentially) convex for $\gamma > 2$. This leads to the introduction of the HTMC norm, which measures function complexity in this setting.

Concurrently, the paper constructs a ResNet-induced function norm, related to a weighted $\ell_1$ measure of the ResNet parameters, capturing how "prunable" a ResNet is for function approximation. Crucially, the HTMC and ResNet norms are connected via a quantitative sandwich bound, establishing both upper and lower estimates between them, and thereby relating circuit minimization and deep learning optimization in the HTMC regime.

Real-Valued Function Computation and the HTMC Regime

Boolean circuit complexity traditionally addresses discrete-valued functions; this paper generalizes circuit size to real-valued function approximation. Given normed functions $$f: \mathbb{R}^{d_\mathrm{in}} \to \mathbb{R}^{d_\mathrm{out}}$$, $C(f, \epsilon)$ denotes the minimal binary circuit size required to $\epsilon$-approximate $f$. The circuit complexity scaling exponent $\gamma$ determines the test error decay rate: for mean squared error over $N$ samples, $R_{\mathrm{test}} = O(N^{-2/(2+\gamma)})$.

The central observation is that when $\gamma > 2$, the set of functions with $C(f, \epsilon) = O(\epsilon^{-\gamma})$ is convex up to constants. Defining the HTMC norm,

$$\|f\|_{H^\gamma} = \max_\epsilon \epsilon^\gamma C(f, \epsilon),$$

makes minimization of $\|f\|_{H^\gamma}$ the continuous analog of MCSP. Theoretical analysis demonstrates that the "unit ball" of this norm is convex up to an $\mathcal{O}(1)$ inflation for all $\gamma > 2$.

Enforcing convexity enables the application of convex optimization machinery for approximating MCSP within this regime—a notable departure from the nonconvex, combinatorial nature of the generic MCSP.

Parameter Complexity and the ResNet Norm

To connect continuous representations with the discrete circuit viewpoint, the paper introduces a complexity measure $R(\theta)$ for a ResNet parameter vector $\theta$, structured as a weighted $\ell_1$ norm which encodes how the function can be pruned while maintaining an $\epsilon$-approximation. This complexity is tied to the sensitivity of the function with respect to its parameters, and is formally connected to the minimal circuit size realizable after pruning.

Parallel to the HTMC norm, a ResNet function norm $\|\cdot\|_{R^\omega}$ is defined via: $$\|f\|_{R^\omega}^\omega = \max_\epsilon \epsilon^{\omega - 1} \min_{\theta: \|f - f_\theta\| \leq \epsilon} R(\theta)$$ This pseudo-norm enjoys properties analogous to the HTMC norm in terms of subadditivity and compositional structure, although it strictly encodes more regularity due to its Lipschitz and Hölder continuity controls.

The Sandwich Theorem: Bridging Discrete and Continuous Complexity

A primary contribution is the establishment of a sandwich inequality: $$\|f\|_{H^{\gamma = 2 \omega + \delta}} + \|f\|_{C^{1/\omega}} \lesssim \|f\|_{R^\omega} \lesssim \|f\|_{H^{\omega - \delta}} + \|f\|_{C^{1/(\omega - \delta)}}$$ where $C^\alpha$ denotes the Hölder norm of order $\alpha$. The left inequality is achieved through a "pruning bound," associating networks with small parameter complexity with functions of low HTMC norm. The right inequality is a "construction bound," demonstrating how to express a complex function as a superposition of functions (Tetrakis functions) with efficient ResNet implementations.

Tetrakis Functions and Vertex Approximation

To analyze the extremal structure of the HTMC norm unit ball, the paper introduces Tetrakis functions, derived from the Tetrakis triangulation of the hypercube:

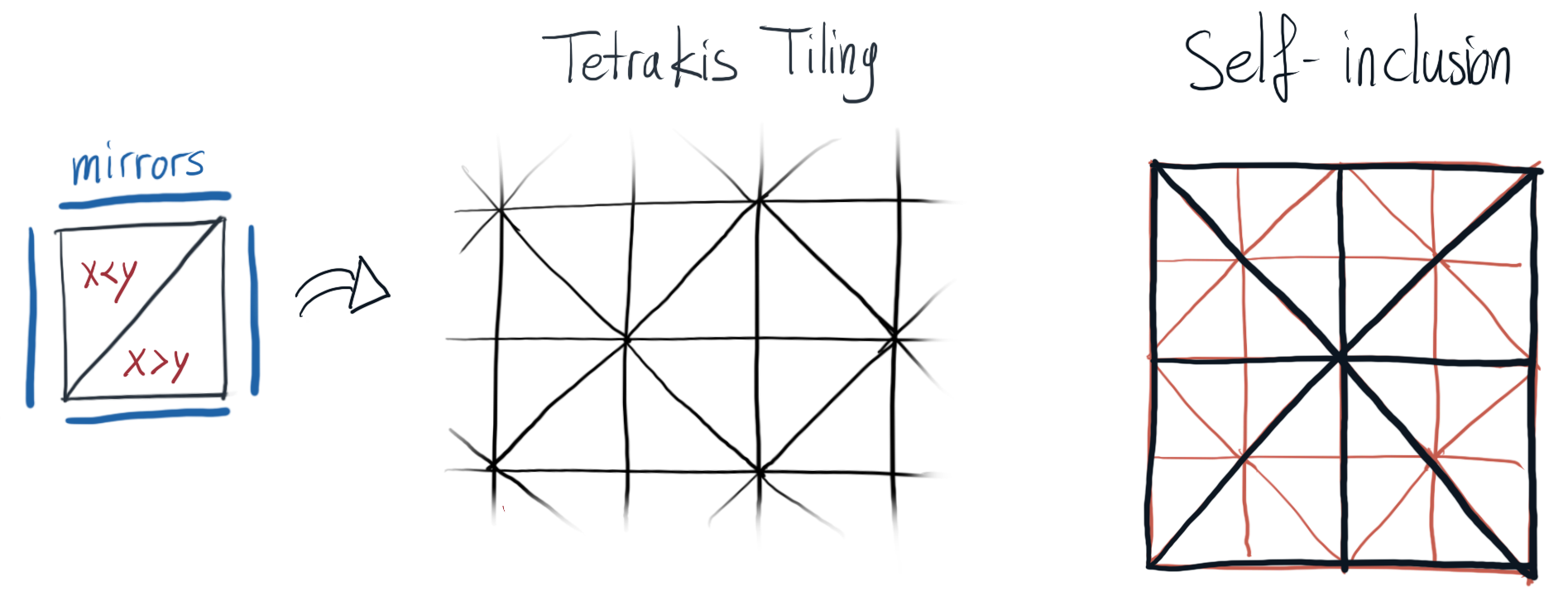
Figure 1: The Tetrakis triangulation in 2D.

These functions serve as atomic approximators, closely representing "vertices" of the (nearly convex) HTMC ball. Any sufficiently regular function with bounded HTMC and Hölder norm can be decomposed as a sum of Tetrakis functions, each admitting an explicit construction as a ResNet with computable parameter complexity, as shown by precise upper complexity bounds.

Generalization and Statistical Rates

Minimizing the HTMC or ResNet norm yields strong statistical performance. The paper derives PAC-style generalization bounds: for the noiseless MSE loss, the excess risk is bounded by

$$R(f) \lesssim \|f\|_{H^\gamma}^{2/(2 + \gamma)} N^{-2/(2+\gamma)}$$

up to logarithmic factors, where $\gamma$ is the relevant complexity exponent. In high dimensions, the HTMC regime allows for rates that do not suffer the curse of dimensionality (unlike standard Hölder classes), supporting the assertion that ResNets are effective at adapting to structured low-complexity functions beyond kernel or classical methods.

Composition and Subadditivity

A significant technical aspect is the convexity and near subadditivity of the complexity measures under function addition and composition. This property is essential not only for the sandwich bound but also for supporting the practical trainability and representation power of DNNs, especially when modeling compositional or hierarchical functions frequently encountered in real-world applications.

Practical and Theoretical Implications

By elucidating the connection between (almost optimal) circuit complexity minimization and ResNet-based deep learning, the theory provides a formal justification for the empirical success of DNNs, especially in high-complexity function approximation domains. The framework opens the possibility for the design of convex optimization algorithms closely approximating MCSP within the HTMC regime; with differentiable surrogates to the ResNet complexity, one could, in principle, achieve gradient-based minimization directly towards minimal-size circuit solutions.

The convexity structure also explains why overparameterized DNNs, trained with greedy methods such as SGD, are capable of learning compositional and hierarchical algorithms. Moreover, the decomposition into Tetrakis functions suggests new algorithmic paradigms, such as Frank-Wolfe-style optimization in the space of atomic circuits.

Prospective Directions

The results indicate several fundamental paths for theoretical and algorithmic development:

• Global convergence analysis: With the convexity of the function space, analysis of gradient descent dynamics in overparameterized DNNs for direct minimization of function complexity or circuit size becomes approachable.
• Architecture generalization: While this paper focuses on ResNets, the principles extend, in principle, to other architectures with suitable norm structures.
• Combinatorially efficient algorithms: The atomic decomposition and convex geometry of HTMC balls may allow optimization strategies for MCSP beyond brute-force exponential methods, albeit with open problems regarding implementation and scalability.

Conclusion

This paper rigorously connects the minimal circuit size problem for real function approximation and optimization over deep neural networks, specifically ResNets, by establishing a convex function space framework within the HTMC regime. The demonstrated equivalence (up to power-law factors) between circuit size minimization and ResNet complexity minimization—with explicit function norms, atomic decompositions, and generalization guarantees—offers a new theoretical grounding for the success of deep learning, particularly in the context of learning structured algorithms and functions inaccessible to classical statistical methods. The theoretical apparatus provided opens the door to convexification strategies, optimization algorithms, and global convergence analysis for DNN-based circuit minimization (2511.20888).