Hierarchical Causal Structure Learning

Abstract: Traditional statistical approaches primarily aim to model associations between variables, but many scientific and practical questions require causal methods instead. These approaches rely on assumptions about an underlying structure, often represented by a directed acyclic graph (DAG). When all variables are measured at the same level, causal structures can be learned using existing techniques. However, no suitable methods exist when data are organized hierarchically or across multiple levels. This paper addresses such cases, where both unit-level and group-level variables are present. These multi-level structures frequently arise in fields such as agriculture, where plants (units) grow within different environments (groups). Building on nonlinear structural causal models, or additive noise models, we propose a method that accommodates unobserved confounders as well as group-specific causal functions. The approach is implemented in the R package HSCM, available at https://CRAN.R-project.org/package=HSCM.

• The paper introduces a Hierarchical Structural Causal Model (HSCM) to capture causal dependencies across group and unit levels, handling unobserved confounders and nonlinear functions.
• It employs a modular approach leveraging CAM for separate estimation of causal structures at multiple hierarchical levels, validated via detailed simulation studies.
• The methodology is applied to agricultural data, providing insights into genotype and environmental interactions influencing maize and winter wheat yields.

Hierarchical Causal Structure Learning: A Detailed Overview

Introduction

Understanding causal relationships in complex hierarchical systems is essential for addressing scientific and practical challenges. The paper "Hierarchical Causal Structure Learning" (2511.20021) presents a methodology for learning causal structures in hierarchical data, which involves variables measured at different levels, such as unit-level within groups. Utilizing a structural causal model (SCM) framework, this approach accounts for unobserved confounders and introduces a method to handle grouped and nested data using nonlinear causal models.

Hierarchical Structural Causal Model (HSCM)

The Hierarchical Structural Causal Model (HSCM) introduced involves a framework to capture causal dependencies across both group-level and unit-level variables. The model structure accommodates unobserved group-level confounders, allowing for a more flexible representation of complex interaction patterns often seen in real-world phenomena.

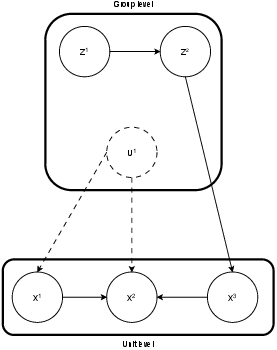
Figure 1: Example of a DAG corresponding to a HSCM with two observed group-level variables, one unobserved group-level confounder, and three unit-level variables.

The HSCM is formulated using equations that define the relationship between observed group-level variables $\bm{Z}$, unobserved group-level confounders $\bm{U}$, and observed unit-level variables $\bm{X}$. The model assumes additive noise and nonlinear causal functions to ensure identifiability, following practices from existing SCM literature. Extensions to HSCM include consideration for group-specific relationships and additional grouping factors, enhancing the model's applicability across diverse datasets.

Causal Structure Learning

Learning the causal structure in hierarchical models leverages existing methodologies designed for single-level SCMs. The proposed method utilizes the CAM approach to estimate causal relationships at both the group and unit levels separately. This modular approach allows for the reliable detection of causal dependencies, even in the presence of confounding factors.

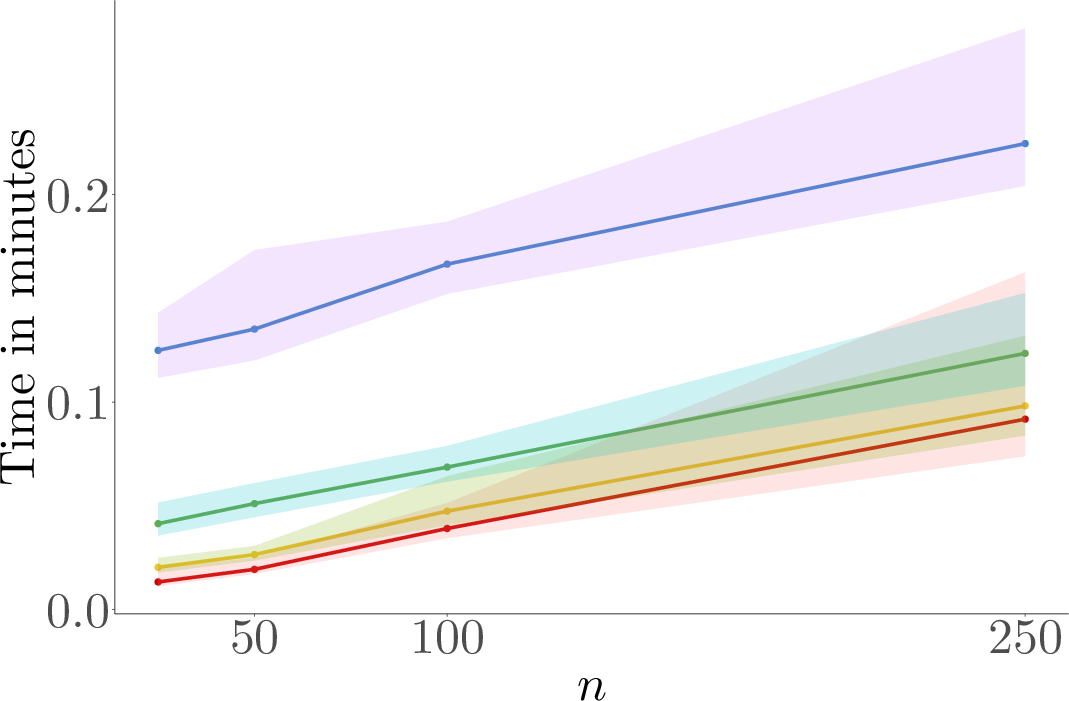
Figure 2: Computation time for the proposed method in minutes. The colors represent different numbers of groups.

The learning procedure is robust to various extensions, such as unobserved unit-level confounders and group-specific functions. The paper outlines a systematic algorithm for estimating causal structures, detailing each step of the process from preliminary neighborhood selection to significance testing.

Simulation Study

A comprehensive simulation study validates the proposed HSCM framework. Various settings were considered, involving different numbers of groups and unit-level observations. Metrics such as Structural Hamming Distance (SHD) and root mean squared error (RMSE) were used to evaluate the accuracy of the estimated causal structure and functions.

Results from these simulations demonstrate the method's efficacy across varying complexity levels and data sizes, highlighting the importance of sufficient sample sizes for accurate causal inference.

Applications on Maize and Winter Wheat Data

The methodology was applied to real-world agricultural datasets, showcasing its practical utility. The estimated DAGs for maize and winter wheat provided insights into the causal factors influencing yield, demonstrating typical findings in agricultural research concerning genotype and environmental interactions.

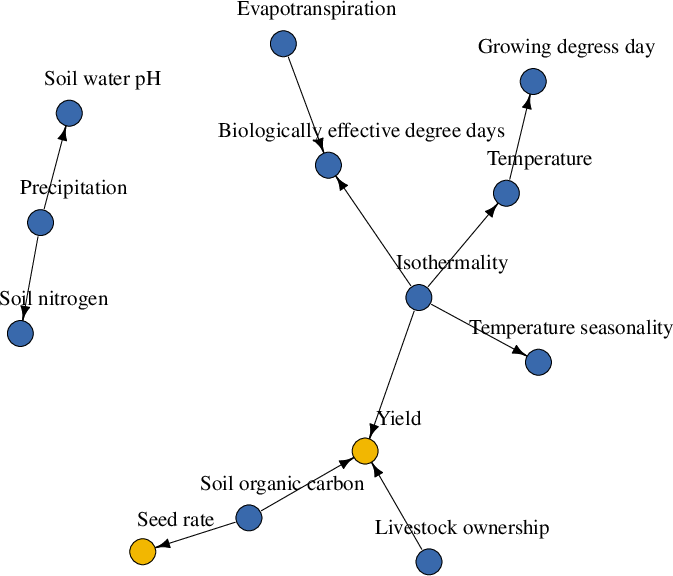
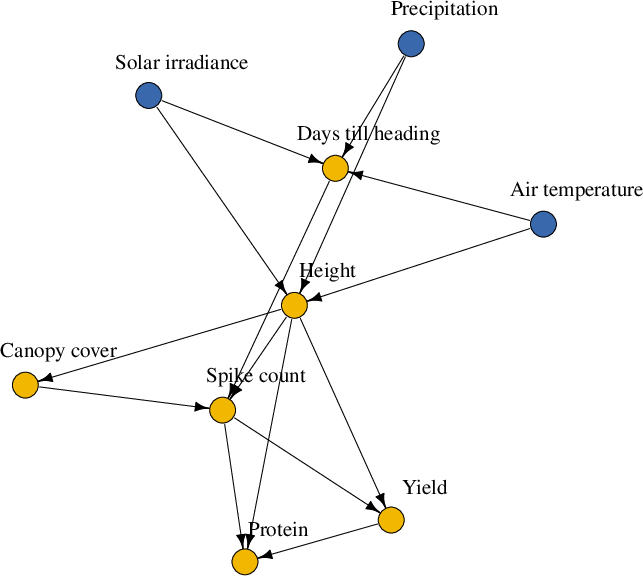
Figure 3: Maize DAG

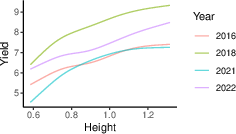
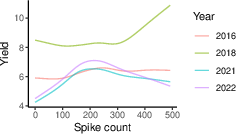
Figure 4: Estimated effect of plant height on yield

In the applications, yield was identified as a trait influenced by several variables, both at the unit and group levels. This aligns with established knowledge in agronomy and emphasizes the model's capability to uncover intricate causal networks within nested data structures.

Conclusion

The "Hierarchical Causal Structure Learning" paper advances causal discovery methodologies by developing a flexible framework to address hierarchical data's complexities. The HSCM model contributes significantly to fields reliant on nested structures, enabling more accurate interpretations of data.

Future research could explore the model's extension to dynamic systems, examine theoretical properties under relaxed assumptions, and assess computational aspects for high-dimensional data. Additionally, applying this methodology to other domains beyond agriculture can substantiate its generalizability and effectiveness in diverse applications.