Financial Information Theory (2511.16339v1)

Abstract: This paper introduces a comprehensive framework for Financial Information Theory by applying information-theoretic concepts such as entropy, Kullback-Leibler divergence, mutual information, normalized mutual information, and transfer entropy to financial time series. We systematically derive these measures with complete mathematical proofs, establish their theoretical properties, and propose practical algorithms for estimation. Using S&P 500 data from 2000 to 2025, we demonstrate empirical usefulness for regime detection, market efficiency testing, and portfolio construction. We show that normalized mutual information (NMI) behaves as a powerful, bounded, and interpretable measure of temporal dependence, highlighting periods of structural change such as the 2008 financial crisis and the COVID-19 shock. Our entropy-adjusted Value at Risk, information-theoretic diversification criterion, and NMI-based market efficiency test provide actionable tools for risk management and asset allocation. We interpret NMI as a quantitative diagnostic of the Efficient Market Hypothesis and demonstrate that information-theoretic methods offer superior regime detection compared to traditional autocorrelation- or volatility-based approaches. All theoretical results include rigorous proofs, and empirical findings are validated across multiple market regimes spanning 25 years of daily returns.

• The paper establishes a rigorous framework by applying measures like entropy, KL divergence, and mutual information to financial time series data.
• It introduces practical estimation techniques using k-nearest neighbor methods that effectively detect market regime shifts and periods of stress.
• The study demonstrates actionable applications such as entropy-adjusted Value at Risk and NMI-based trading signals for enhanced risk management.

Financial Information Theory: An Overview

Introduction

The paper "Financial Information Theory" (2511.16339) presents a comprehensive approach to analyzing financial time series using information-theoretic concepts. Traditional statistical tools often rely on second-order moments or linear correlations, which may not adequately capture complex, nonlinear dependencies and structural changes in financial markets. By applying information-theoretic measures such as entropy, Kullback-Leibler (KL) divergence, mutual information, normalized mutual information (NMI), and transfer entropy, this paper provides robust, model-free techniques for assessing market dynamics without assuming linearity or Gaussianity of financial data.

Theoretical Framework

The authors establish a rigorous theoretical foundation for using information-theoretic measures in finance, complete with mathematical proofs and practical estimation algorithms. The paper emphasizes four main contributions:

1. Rigorous Formulation: Core information-theoretic quantities, including entropy, KL divergence, mutual information, and transfer entropy, are thoroughly reviewed and formalized with proofs of their properties.
2. Estimation Techniques: Practical methods for calculating entropy, NMI, and transfer entropy from financial time series data are proposed, focusing on k-nearest neighbor ($k$-NN) approaches.
3. Empirical Validation: The application of these measures using S&P 500 data from 2000 to 2025 demonstrates their efficacy in regime detection and market efficiency testing.
4. Practical Applications: Recommendations for entropy-adjusted Value at Risk (VaR) and NMI-based market efficiency diagnostics are offered, showcasing the actionable insights these techniques provide for risk management and portfolio construction.

Empirical Findings

The empirical section applies these concepts to the S&P 500 returns, validating the theory over a 25-year period. Key findings include:

• Entropy and Market Stress: Shannon entropy effectively captures periods of high market uncertainty, with notable spikes during the 2008 financial crisis and the COVID-19 pandemic, reflecting wider distribution characteristics during volatile periods.

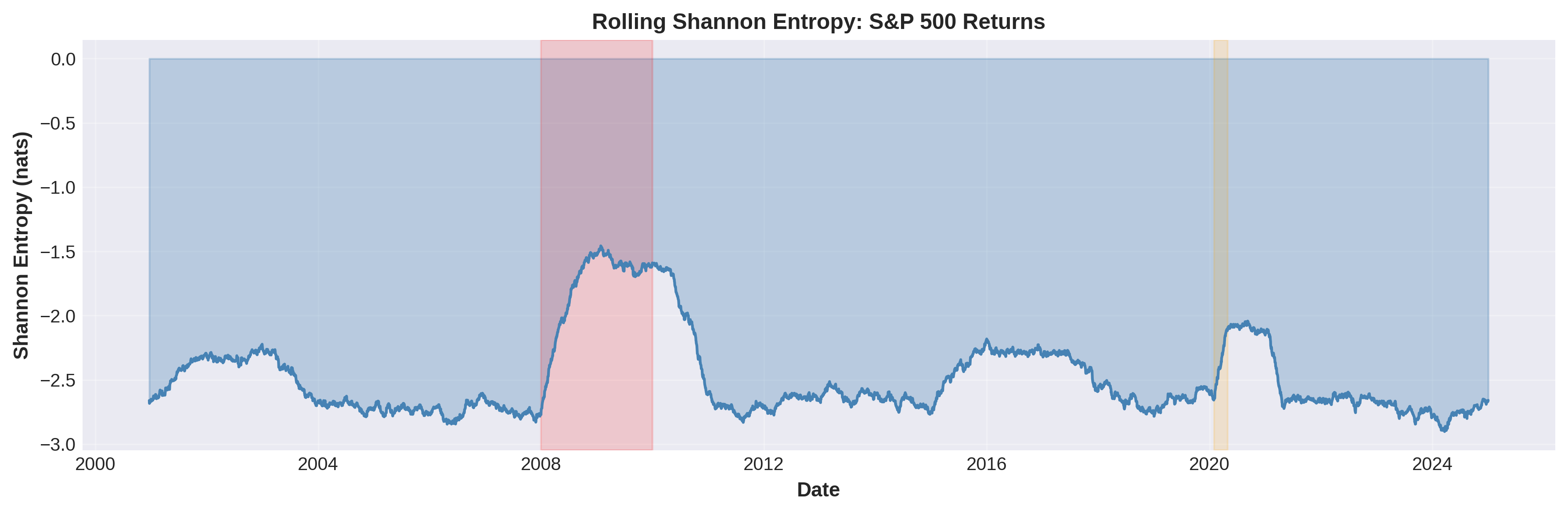
  Figure 1: Rolling Shannon Entropy for S&P 500 Returns (2000--2025).

• Regime Detection via KL Divergence: KL divergence identifies structural breaks and market regime shifts more effectively than volatility-based methods, with significant spikes corresponding to major financial disruptions.

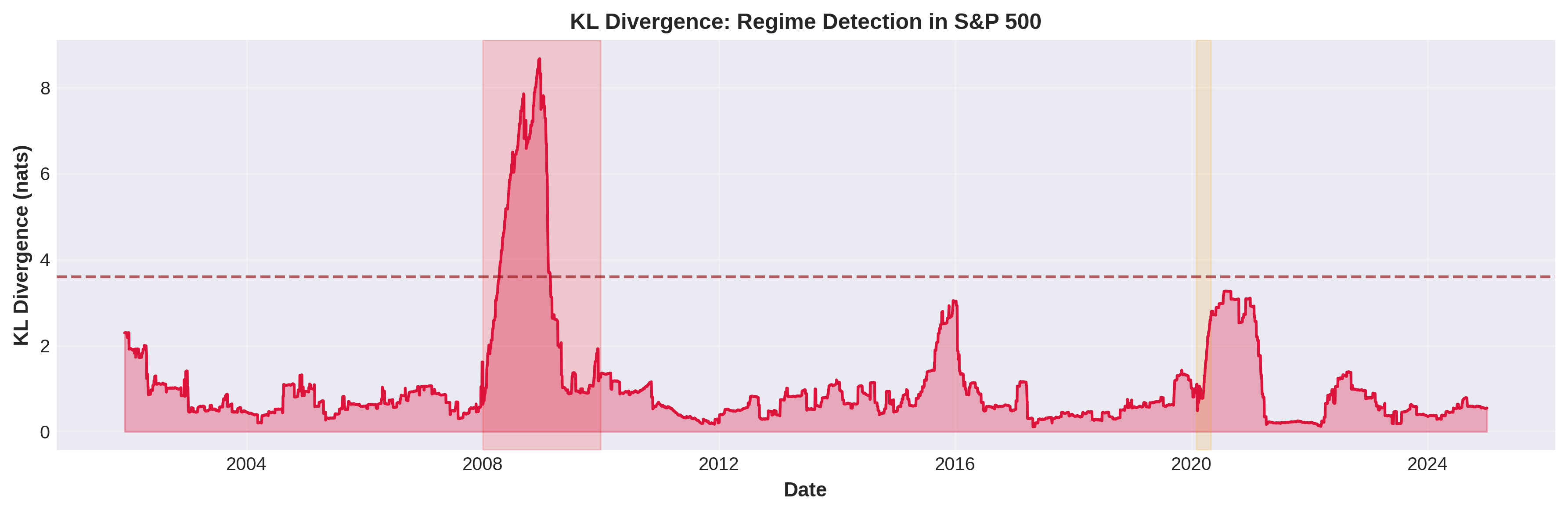
  Figure 2: KL Divergence for Regime Detection in S&P 500 (2000--2025).

• Market Efficiency and NMI: NMI remains low under normal conditions, supporting the Efficient Market Hypothesis (EMH), while deviations during crises indicate temporary market inefficiency allowing for potential exploitation via trading strategies.

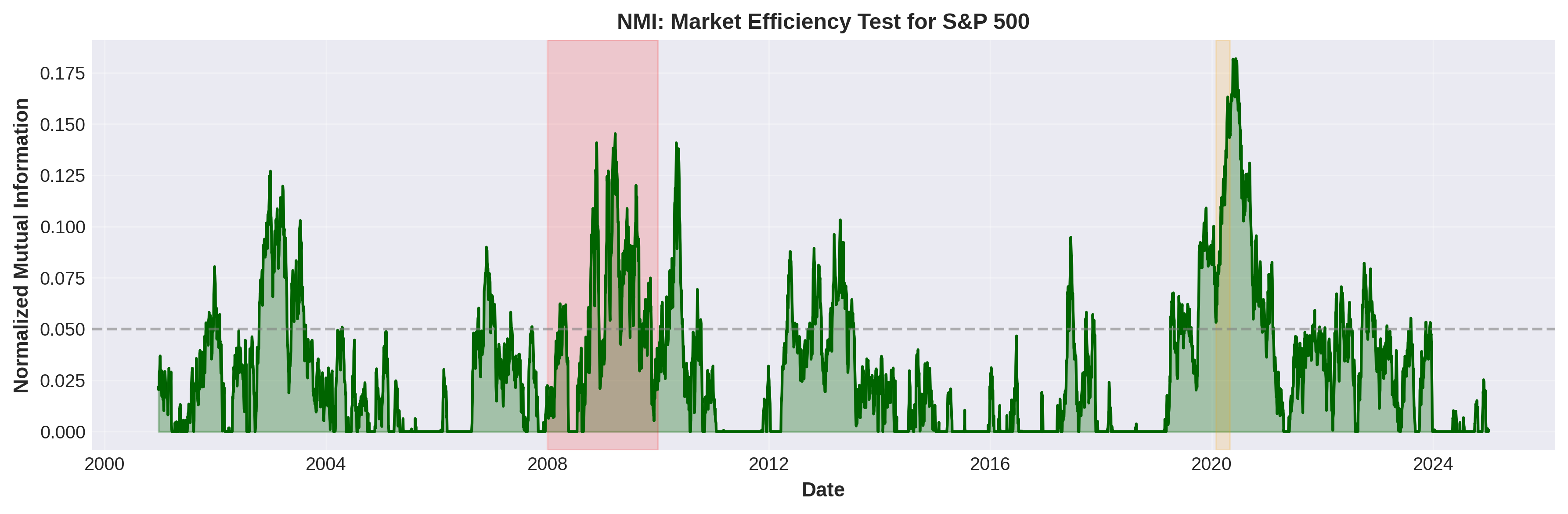
  Figure 3: Normalized Mutual Information (NMI) for Market Efficiency Testing (2000--2025).

Practical Implications

The research advances the application of information theory in finance through several practical tools:

• Entropy-Adjusted VaR: Enhances traditional VaR models by incorporating KL divergence to adjust risk limits dynamically, reflecting real-time market conditions.
• Information-Theoretic Diversification: Suggests portfolio strategies based on entropy measures, ensuring a diversified allocation by minimizing total correlation among assets.
• NMI-Based Trading Signals: Proposes adaptive trading strategies that detect and exploit inefficiencies signaled by elevated NMI values, specifically during periods of structural change.

Theoretical and Practical Advancements

This paper contributes substantially to the understanding of market dynamics through the lens of information theory, providing both theoretical advancements and practical algorithms for market participants. The techniques presented allow for sophisticated diagnostics of market regimes, more robust risk management practices, and nuanced assessments of market efficiency that go beyond traditional autocorrelation and volatility metrics.

Conclusion

Financial Information Theory as formulated in this paper serves as a powerful framework for analyzing financial time series, with its theoretical constructs effectively translating into practical financial tools. By utilizing entropy, KL divergence, and NMI, the research presents a model-free and robust approach to understanding the complex dynamics of financial markets, ensuring these methods will remain relevant as financial complexity continues to evolve.