Better LLM Reasoning via Dual-Play (2511.11881v2)

Abstract: LLMs have achieved remarkable progress through Reinforcement Learning with Verifiable Rewards (RLVR), yet still rely heavily on external supervision (e.g., curated labels). Adversarial learning, particularly through self-play, offers a promising alternative that enables models to iteratively learn from themselves - thus reducing reliance on external supervision. Dual-play extends adversarial learning by assigning specialized roles to two models and training them against each other, fostering sustained competition and mutual evolution. Despite its promise, adapting dual-play training to LLMs remains limited, largely due to their susceptibility to reward hacking and training instability. In this paper, we introduce PasoDoble, a novel LLM dual-play framework. PasoDoble adversarially trains two models initialized from the same base model: a Proposer, which generates challenging questions with ground-truth answers, and a Solver, which attempts to solve them. We enrich the Proposer with knowledge from a pre-training dataset to ensure the questions' quality and diversity. To avoid reward hacking, the Proposer is rewarded for producing only valid questions that push the Solver's limit, while the Solver is rewarded for solving them correctly, and both are updated jointly. To further enhance training stability, we introduce an optional offline paradigm that decouples Proposer and Solver updates, alternately updating each for several steps while holding the other fixed. Notably, PasoDoble operates without supervision during training. Experimental results show that PasoDoble can improve the reasoning performance of LLMs. Our project page is available at https://hcy123902.github.io/PasoDoble.

• The paper demonstrates the effectiveness of dual-play in LLM reasoning by introducing PasoDoble, which leverages competitive interactions between a proposer and solver.
• It integrates a robust reward function and external knowledge to generate challenging math questions evaluated on benchmarks like AIME and MATH-500.
• The dual-agent paradigm offers scalability and insights into adversarial training dynamics, encouraging further exploration of multi-agent and domain-specific extensions.

Dual-Play for LLM Reasoning: An Expert Review of PasoDoble

Motivation and Context

Recent advancements in LLMs have leveraged Reinforcement Learning with Verifiable Rewards (RLVR), effectively utilizing outcome-based supervision for tasks requiring complex reasoning. However, RLVR and related label-free approaches are bottlenecked by their reliance on high-quality, curated supervision—limiting their scalability to domains with scarce labeled data. In response, adversarial learning paradigms, particularly self-play and dual-play, have emerged as promising alternatives, enabling models to create their own training signals.

Dual-play, characterized by two interacting agents with specialized roles, is an underexplored but theoretically compelling adversarial protocol for LLM training. The core challenge is adapting dual-play for LLMs without succumbing to reward hacking and training instability. The "Better LLM Reasoning via Dual-Play" (2511.11881) introduces PasoDoble, a dual-play framework that directly addresses these obstacles.

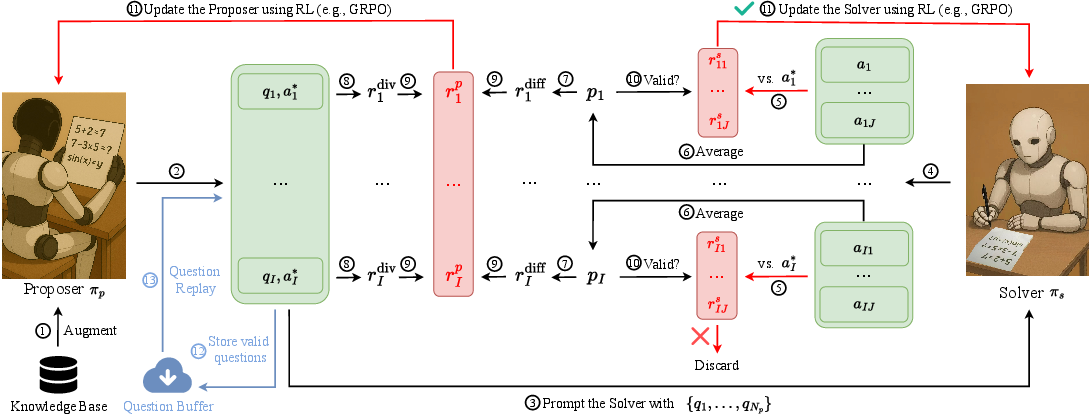
Figure 1: PasoDoble comprises Proposer, Solver, Knowledge Base, and Question Buffer for adversarial dual-play training.

PasoDoble Framework: Formulation and Training

PasoDoble instantiates dual-play as a competitive interaction between a Proposer and a Solver, both initialized from a common pre-trained LLM. The Proposer generates challenging math questions and ground-truth answers, drawing upon a knowledge base (MegaMath-Pro-Max), while the Solver attempts to solve these questions multiple times. The training loop is structured to ensure that:

• The Proposer's reward is inversely correlated with Solver accuracy (harder questions, higher reward) and augmented by a diversity term to prevent repetition.
• The Solver is rewarded strictly on correctness, confined to questions deemed valid (passing rates above a threshold, diversity exceeding cutoff).
• Both agents are updated synchronously (online), or alternately (offline), with the latter decoupling updates to enhance stability.

To prevent reward hacking (e.g., the Proposer generating ill-formed or unsolvable questions), the reward function incorporates rigorous validity checks. The necessity of external knowledge is specifically motivated by the need to maintain question/answer quality—particularly since both roles are initially weak and lack domain specificity.

PasoDoble operates without explicit supervision during adversarial training, leveraging only prior pre-training data for initial grounding.

Experimental Results: Reasoning Gains and Scaling Properties

PasoDoble was evaluated across a suite of math benchmarks, including AIME, AMC, GSM8K, MATH-500, and OlympiadBench, using multiple base models (Qwen2.5 and Qwen3 variants from 0.5B to 4B parameters).

Strong numerical results are observed:

• For Qwen3-1.7B-Base, average pass@1 accuracy improved by 11.42 (online) and 12.75 (offline) points.
• The largest model, Qwen3-4B-Base, gained 15.96 (online) and 15.10 (offline) points.
• Performance gains are monotonic with model scale.
• Improvements are sustained over hundreds of update steps, contrasting sharply with R-Zero, where training plateaus after three iterations.

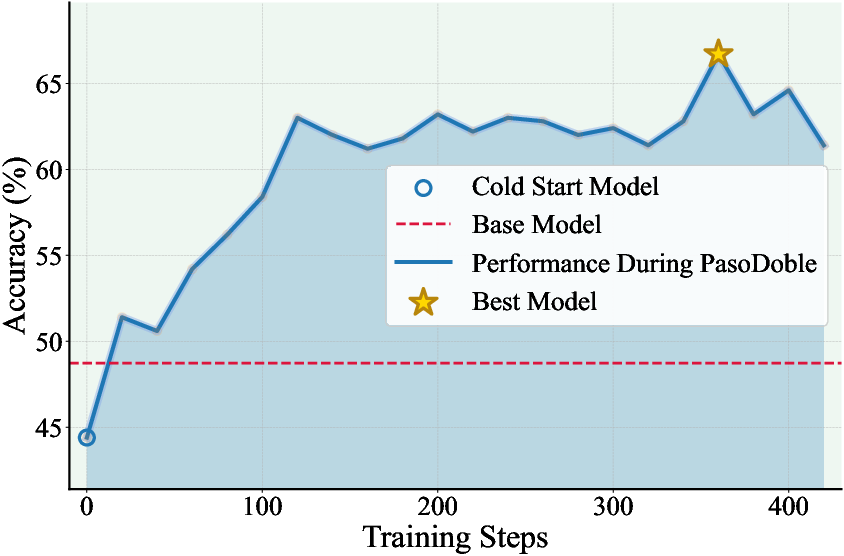
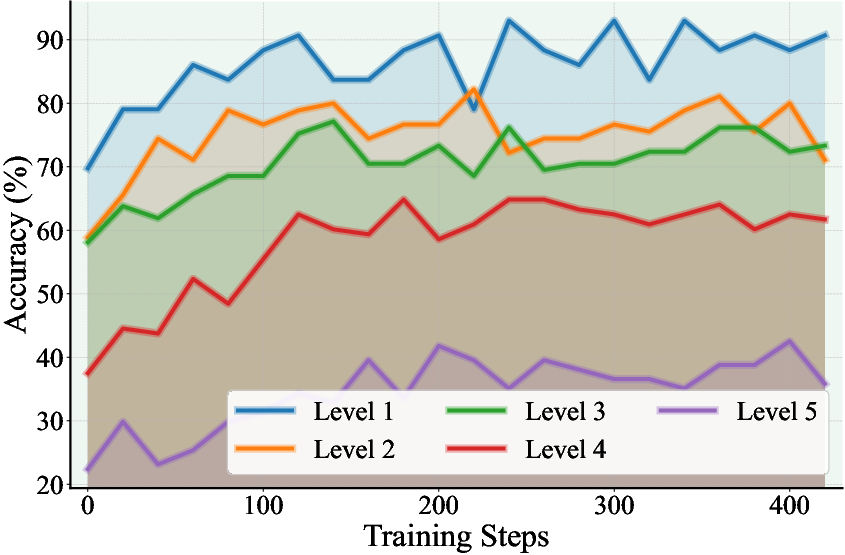
Figure 2: Accuracy trajectory of PasoDoble-trained models on MATH-500 demonstrates consistent improvement.

Ablation results reveal robust requirements:

• Joint training of Proposer and Solver is essential; freezing either agent rapidly saturates performance.
• The external knowledge base disproportionately benefits larger models; for small models, its absence may actually improve sample quality due to alignment with model capacity.
• Removing ground-truth answers (i.e., pure unsupervised feedback) collapses performance, indicating the critical role of verifiable signal.
• Diversity rewards and careful thresholding for question retention are also necessary to sustain progress and prevent degenerate learning.

Analysis of Training Dynamics and Question Generation

PasoDoble enables nuanced control and measurement of the evolving interaction between Proposer and Solver:

• Training dynamics on MATH-500 show rapid accuracy gains primarily in the earliest phase, followed by slower, oscillatory improvements.
• Problem difficulty distribution evolves toward intermediate and hard questions, with diversity and sampling efficiency improving across iterations.
• Empirical assessment of Proposer outputs using GPT-5-mini demonstrates high-quality retrieval (accuracy >70%) for questions with passing rates above threshold, validating the filtering strategy.
• Proposer-composed questions are not simple copies from the knowledge base; analyses of ROUGE-L and EM against internal candidate completions show strong novelty, confirming true reasoning rather than memorization.

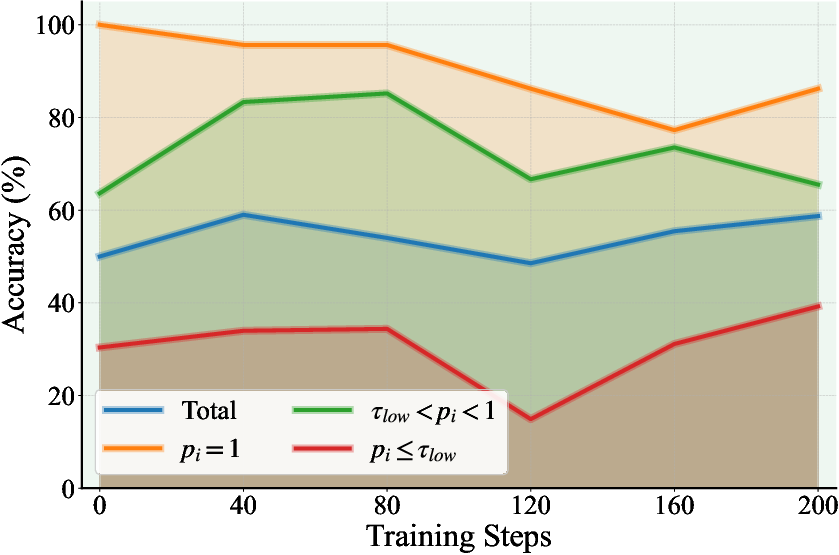
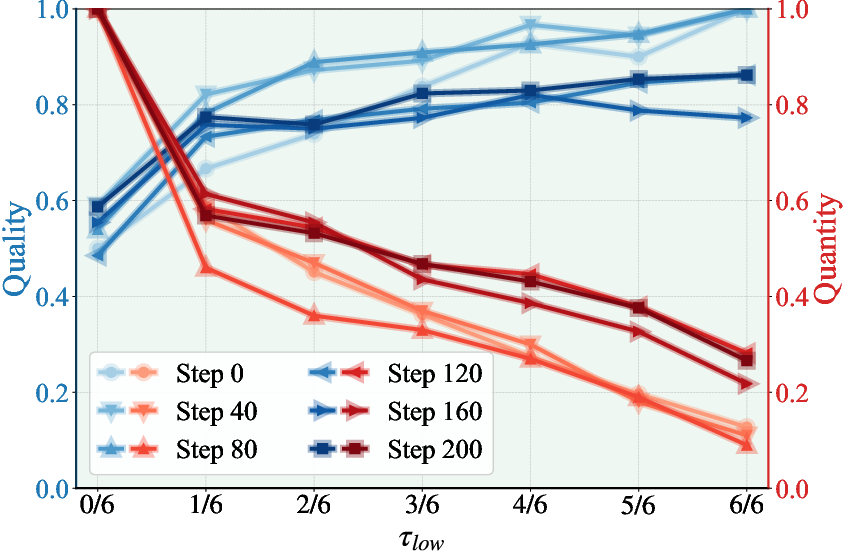
Figure 3: Fraction of Proposer-generated QA pairs matching reference answers as a function of passing-rate threshold.

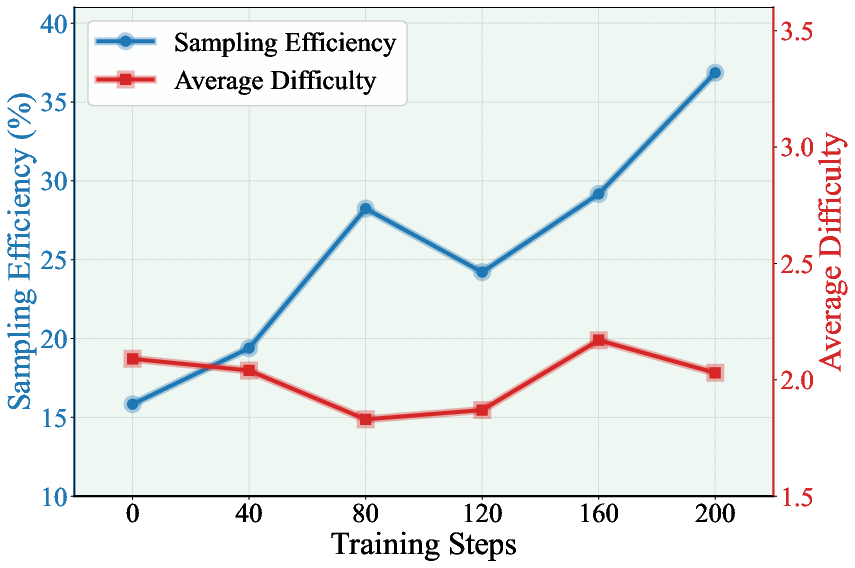
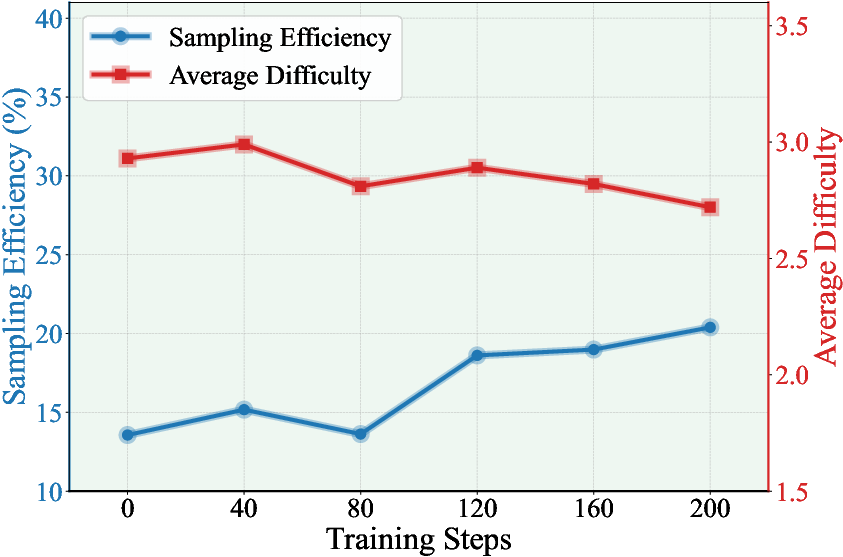
Figure 4: Average question difficulty and sampling efficiency trends with and without external knowledge.

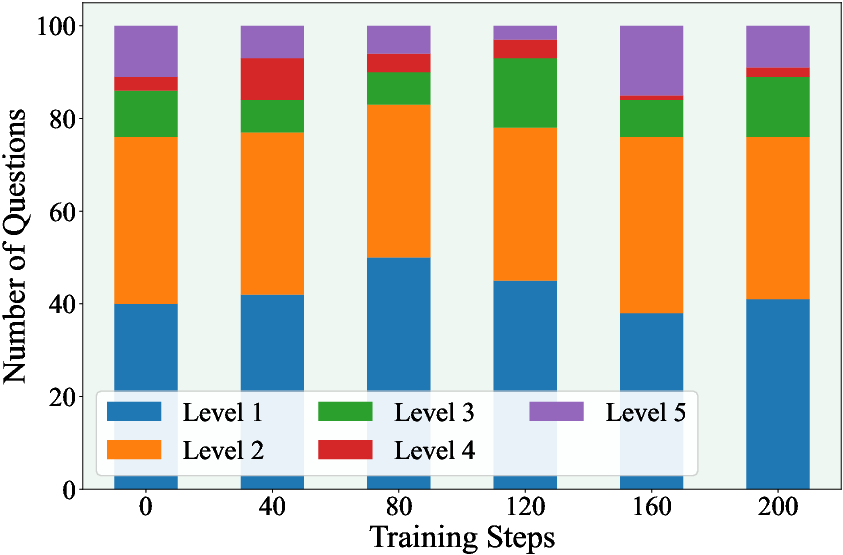
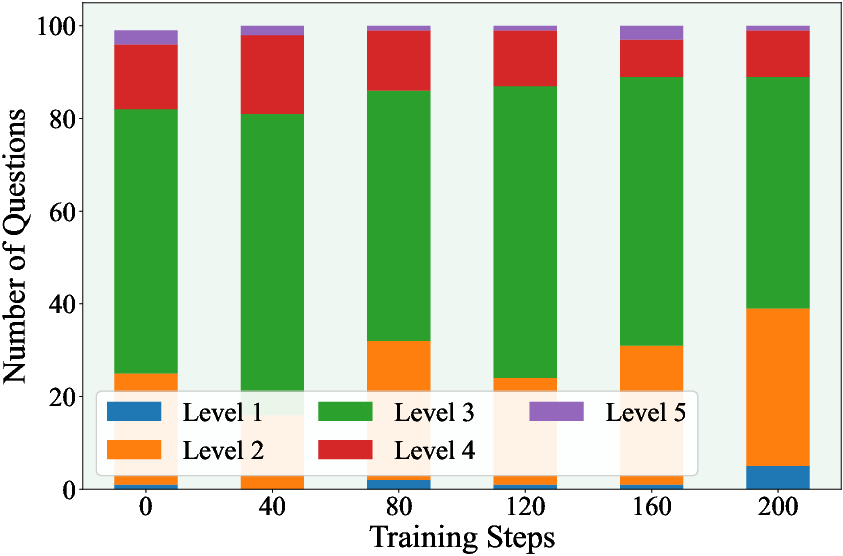
Figure 5: Number of generated questions per difficulty level throughout training.

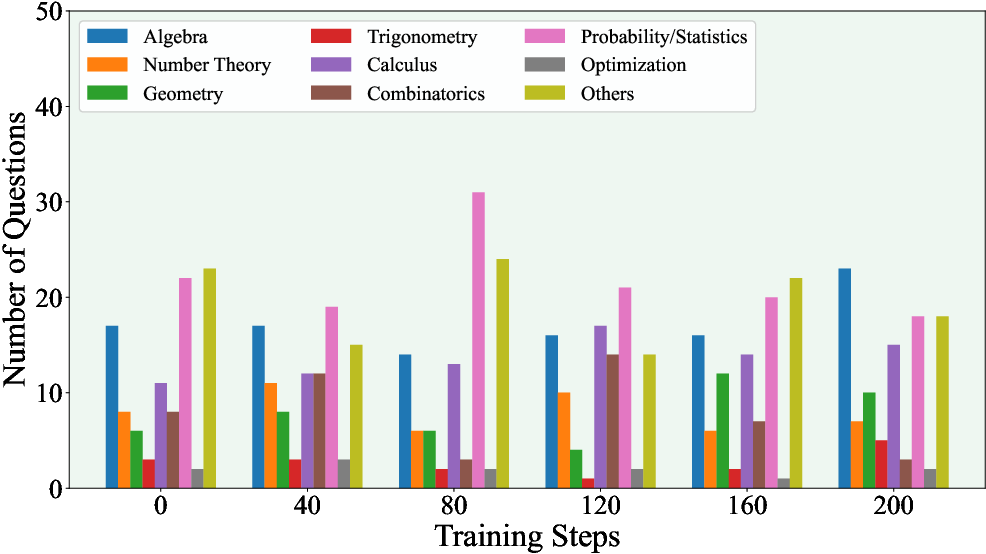
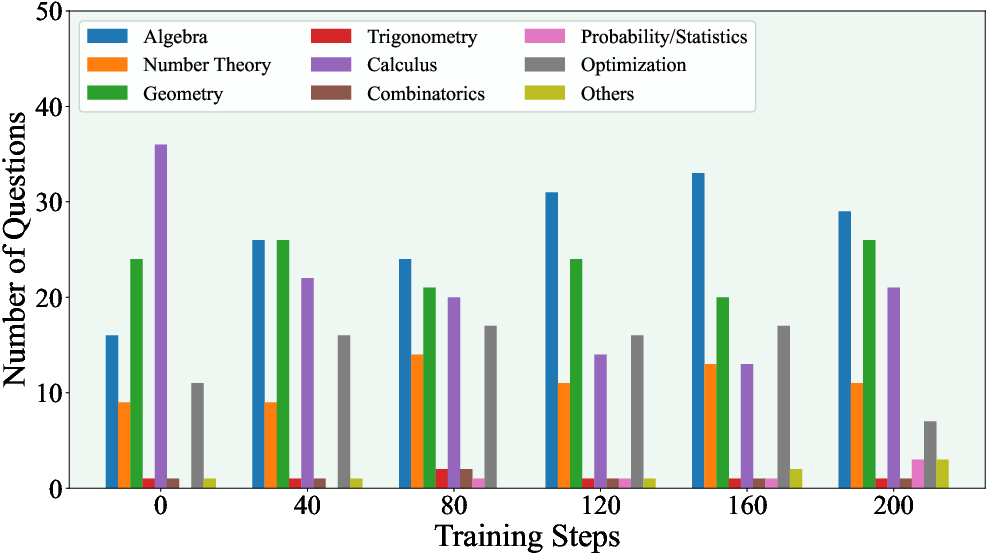
Figure 6: Domain diversity in generated questions, showing wide coverage when external knowledge is present.

Implications and Theoretical Extensions

PasoDoble demonstrates that competitive co-evolution of agents (dual-play) enables LLMs to self-generate challenging, diverse, and high-quality training signals without direct supervision, effectively bridging pre-training and post-training. The approach introduces complementary specialization—an adversary to generate tasks, a solver to attack them—replacing supervision with an automated curriculum aligned to the model's competence.

The empirical evidence encourages several theoretical developments:

• Adversarial multi-agent protocols could further be generalized (e.g., triple-play with proposer, solver, verifier, or four-play with critics and knowledge retrievers), introducing richer collaborative and competitive training dynamics.
• Specialized conditioning of the knowledge base, perhaps adaptive to model performance, may yield meta-curricula that amplify scaling gains and domain transfer.
• Mechanisms for preserving valid but hard QA pairs may be necessary to prevent loss of signal as models saturate simpler problem classes.

Practically, PasoDoble suggests a scalable direction for domain-specialized reasoning LLMs, particularly in settings with minimal labeled data.

Limitations and Future Directions

Observed limitations include:

• Gains saturate for smallest (<1B) models and narrow significantly for out-of-domain tasks such as GPQA/SuperGPQA, indicating domain specificity and scale sensitivity.
• Even with high-quality math knowledge, improvements asymptote after several hundred steps, implying a need for mechanisms (e.g., adaptive buffer eviction, meta-proposer strategies) that can sustain long-term co-evolution.
• Generalization to broader domains and integration with multimodal or agentic protocols remain open research challenges.

Conclusion

PasoDoble provides a technically sound and empirically validated dual-play framework for LLM reasoning enhancement. Through adversarial co-evolution between Proposer and Solver, guided by judicious reward design and external knowledge integration, it achieves significant and scaling improvements in mathematical reasoning—without explicit supervision. The protocol bridges critical gaps between pre-training knowledge anchoring and post-training curriculum, offering a template for next-generation, label-efficient LLM training pipelines.

Continued progress will require refining dual-play for further stability and generality, exploring multi-agent extensions, and developing robust techniques for transfer outside the math domain. PasoDoble sets a precedent for adversarially-shaped, self-supervised model evolution in language modeling.