Drift Estimation for Diffusion Processes Using Neural Networks Based on Discretely Observed Independent Paths (2511.11161v1)

Abstract: This paper addresses the nonparametric estimation of the drift function over a compact domain for a time-homogeneous diffusion process, based on high-frequency discrete observations from $N$ independent trajectories. We propose a neural network-based estimator and derive a non-asymptotic convergence rate, decomposed into a training error, an approximation error, and a diffusion-related term scaling as ${\log N}/{N}$. For compositional drift functions, we establish an explicit rate. In the numerical experiments, we consider a drift function with local fluctuations generated by a double-layer compositional structure featuring local oscillations, and show that the empirical convergence rate becomes independent of the input dimension $d$. Compared to the $B$-spline method, the neural network estimator achieves better convergence rates and more effectively captures local features, particularly in higher-dimensional settings.

• The paper proposes a neural network estimator that accurately recovers the drift function from high-frequency, discretely observed SDE trajectories.
• The paper demonstrates superior performance over spline methods by resolving local drift fluctuations and overcoming the curse of dimensionality.
• The paper provides a detailed theoretical analysis with a non-asymptotic L2 risk bound decomposed into training, approximation, and diffusion-induced errors.

Drift Estimation for High-Frequency Diffusion Trajectories via Neural Networks

Problem Formulation and Background

The paper addresses the nonparametric estimation of the drift component $b(\cdot)$ for a time-homogeneous diffusion process governed by the SDE

$dX_t = b(X_t)\,dt + \sigma(X_t)\,dB_t,$

where $X_t\in\mathbb{R}^d$, with access to $N$ i.i.d. high-frequency discretely observed independent trajectories. Unlike approaches assuming ergodicity or infinite time horizons, the focus is on fixed time intervals, and estimation of the drift is constructed for a compact domain, typically $[0,1]^d$. The data regime considered is particularly relevant in applications where repeated experimentation or simulation yields multiple short, densely sampled stochastic trajectories, common in physical and biological systems and experimental settings.

Traditional statistical approaches for drift estimation in SDEs have relied on kernel methods, series estimators (e.g., $B$-splines), or, in recent work, deep learning-based function approximation. While methods leveraging the long-time regime ($T\rightarrow\infty$) have well-developed theory, theoretically-underpinned neural network-based estimators in the high-frequency, fixed-horizon, multi-path setting are far less studied.

Neural Network Drift Estimator: Construction and Theoretical Guarantees

The authors propose to estimate the drift function component-wise via ReLU neural networks acting on the observation domain, employing the empirical squared-loss over discrete increments as the objective:

$$Q_{\mathcal{D}_N}(f) = \frac{1}{NM} \sum_{n=1}^{N} \sum_{m=0}^{M-1} \left( Y_{t_m}^{(n)} - f(\bar{X}_{t_m}^{(n)}) \right)^2,$$

where $Y_{t_m}^{(n)}$ is the increment-based estimate of the drift at $t_m$ along path $n$. The estimator $\hat{f}_N$ is the outcome of empirical risk minimization (ERM) over a sparsity-constrained, bounded ReLU network class. The theoretical analysis yields a non-asymptotic $L^2$ estimation risk upper bound that decomposes as:

1. Training Error: captures suboptimality in practical stochastic optimization relative to the ERM minimizer.
2. Approximation Error: reflects the distance between the true drift function and its best neural network approximant in the chosen class.
3. Diffusion-induced Error: a process-dependent term scaling as ${\log N}/{N}$, quantifying the impact of temporal and sample dependence.

For compositional functions, the analysis leverages network approximation properties (via depth and width scaling), yielding explicit rates analogous to those known for nonparametric regression with neural networks.

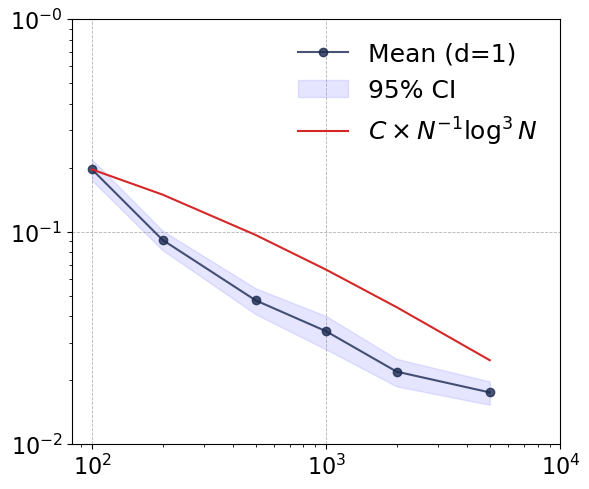
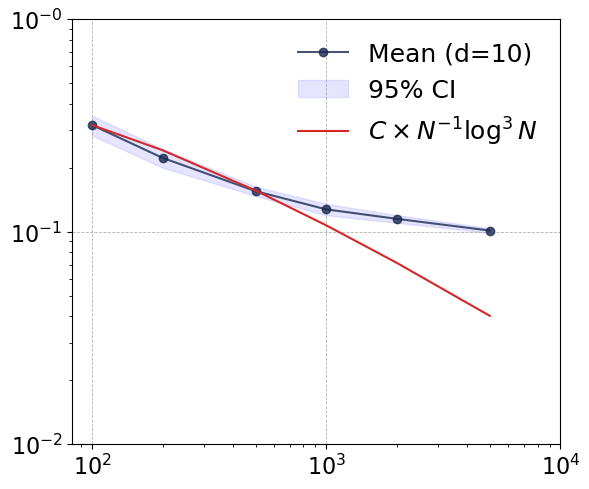
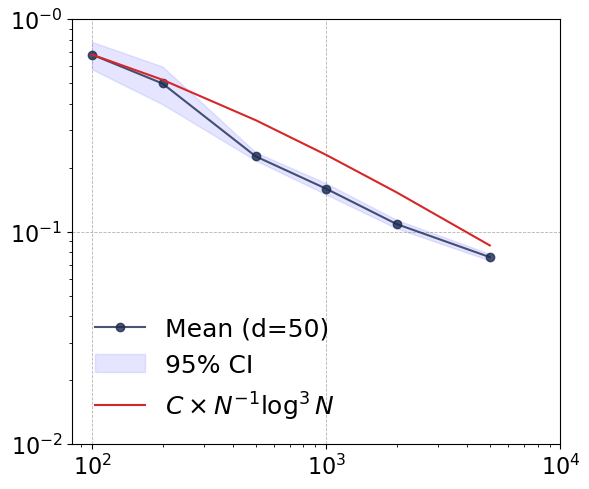
Figure 1: Convergence rates of the proposed estimator across dimensions $d=1,2,10,50$, demonstrating dimension-robust empirical performance.

Numerical Results: High-Dimensional and Comparison Analysis

A central component of the experimental paper is the comparison of the neural estimator with a $B$-spline-based method across varying input dimensions and training sample sizes. The drift function for assessment is chosen to exhibit strong local fluctuations and compositional structure, emphasizing the importance of expressive approximators.

Empirical convergence rates are tracked in terms of log-log error-vs-sample curves. Notably, as dimension increases ($d=1 \rightarrow 50$), the neural estimator maintains convergence rates close to the theoretical envelope $O(N^{-1}\log^3 N)$, and its empirical error decouples from input dimension for large $N$. This phenomenon is consistent with well-chosen network hyperparameters and the compositional smoothness of the test function.

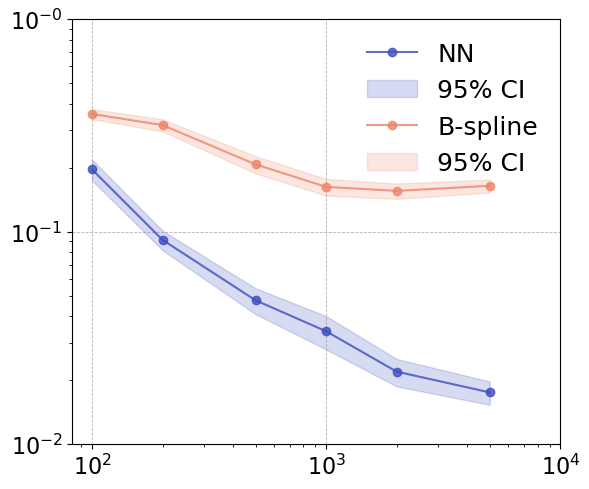
Figure 2: Convergence rate comparison for $d=1$ and $d=2$ between neural network and $B$-spline estimators.

When benchmarked against the $B$-spline approach, the neural estimator exhibits both faster risk decay and markedly improved recovery of local fluctuations, especially as $d$ increases. The $B$-spline approach suffers from the curse of dimensionality due to tensor-product basis construction, which quickly results in intractable memory requirements; for moderate $d$, storing basis matrices becomes computationally prohibitive.

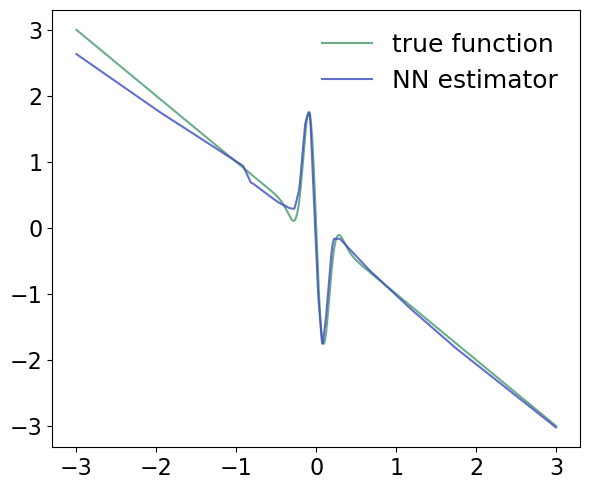
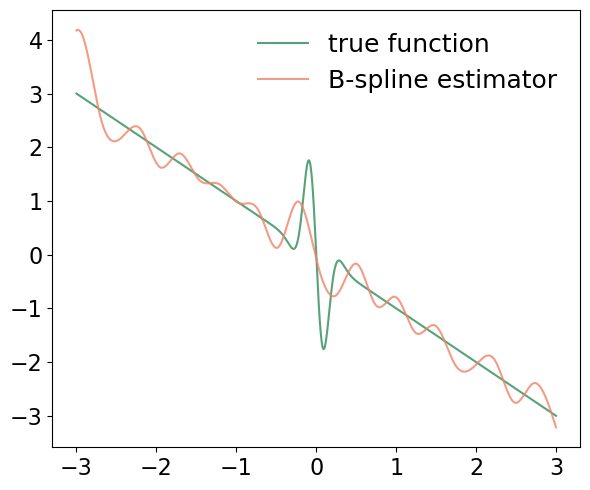
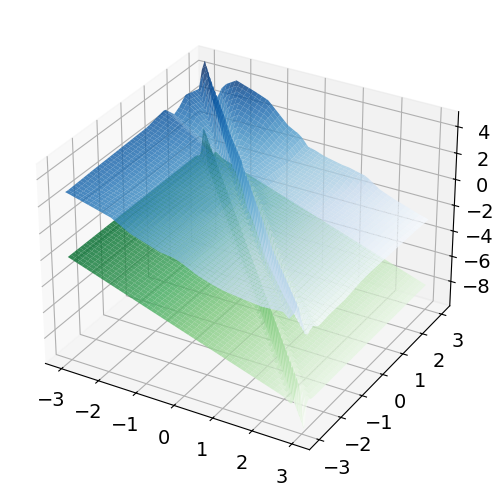
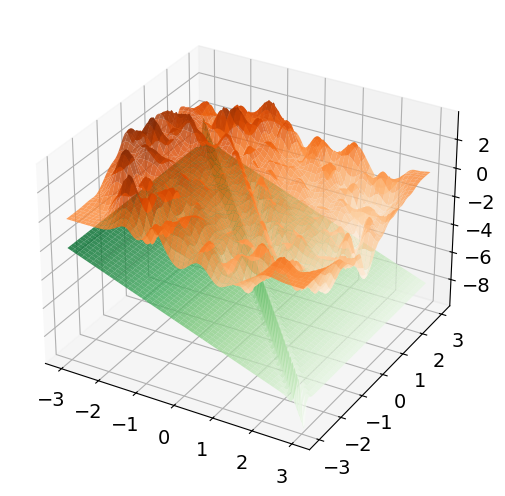
Figure 3: Neural network estimator's output for $d=1$—faithfully capturing local oscillatory structure in the drift.

The performance gap is further highlighted in the estimator's ability to recover local drift features: the neural estimator resolves rapid local change robustly, while the spline-based estimator oversmooths and fails in higher dimensions.

Complexity, Scalability, and Practical Considerations

Memory and computational analysis substantiate the scalability of the neural estimator. For the $B$-spline estimator, parameter count—and thus memory—scales exponentially in $d$. In contrast, the neural estimator's resource usage scales at most linearly (contingent upon network architecture), making it feasible for high-dimensional settings under reasonable hardware assumptions.

The neural estimator's practical feasibility is reinforced by the dataset regime: small-$T$, large-$N$, and high-frequency sampling, as commonly seen in experimental sciences and synthetic models.

Theoretical Implications and Future Directions

The presented analysis deepens the bridge between statistical learning theory for neural networks and stochastic process inference. The main results demonstrate that, for drift estimation with repeated high-frequency trajectory data, neural ERM achieves controlled error rates that are competitive or superior to classical nonparametric approaches. The explicit handling of temporal dependence in error decomposition is a significant advancement.

Possible future developments include:

• Extending theoretical results to dependent path settings or correlated noise.
• Incorporating adaptive network architecture selection via data-driven procedures.
• Exploring robustness under model mismatch (i.e., when the true SDE deviates from the assumed generative model).
• Applying uncertainty quantification approaches, including Bayesian neural network variants, for inferential confidence.

Conclusion

This work provides a theoretically-supported and empirically validated neural network framework for nonparametric drift estimation from high-frequency, independently observed SDE trajectories. The estimator achieves fast, nearly dimension-independent convergence, robustly recovers local structure missed by spline methods, and scales efficiently in high-dimensional regimes. These properties make it a compelling tool for applied stochastic modeling and provide a rigorous foundation for further methodological advances in neural inference for stochastic dynamical systems.