Eigenfunctions of deformed Schrödinger equations (2511.10636v1)

Abstract: We study the spectral problems associated with the finite-difference operators $H_N = 2 \cosh(p) + V_N(x)$, where $V_N(x)$ is an arbitrary polynomial potential of degree $N$. These systems can be regarded as a solvable deformation of the standard Schrödinger operators $p^2 + V_N(x)$, and they arise naturally from the quantization of the Seiberg-Witten curve of four-dimensional, $\mathcal{N} = 2$, SU($N$) supersymmetric Yang-Mills theory. Using the open topological string/spectral theory correspondence, we construct exact, analytic eigenfunctions of $H_N$, valid for arbitrary polynomial potentials and describing both bound and resonant states. Our solutions are entire in $x$ for generic values of the energy, and become $L^2$-normalizable only at a discrete set of energies. An interesting feature of these Hamiltonians is the existence of special loci in the parameter space of the potential, the so-called Toda points. The eigenfunctions exhibit enhanced decay at these points, leading to spectral degeneracies for confining potentials and to a real energy spectrum for unbounded ones. Our results provide a rare example of a quantum-mechanical spectral problem that is exactly solvable, admitting explicit, analytic eigenfunctions for both bound and resonant states.

• The paper presents an explicit construction of analytic eigenfunctions for deformed Schrödinger operators with arbitrary polynomial potentials, addressing both bound and resonant states.
• It employs techniques from the open TS/ST correspondence and Coulomb branch parameters to cancel singularities and produce entire eigenfunctions.
• The work reveals a breakdown of the standard oscillation theorem and uncovers enhanced spectral degeneracies at special quantized moduli known as Toda points.

Analytic Eigenfunctions for Deformed Schrödinger Operators

Introduction

The paper establishes a novel class of exactly solvable quantum spectral problems described by difference operators of the form $H_N = 2 \Lambda^N \cosh(p) + V_N(x)$, where $V_N(x)$ is a polynomial potential of degree $N$. These operators constitute a solvable deformation of standard Schrödinger operators and emerge naturally from the quantization of the Seiberg-Witten curve associated with four-dimensional $\mathcal{N}=2$ SU($N$) supersymmetric Yang-Mills theory. The core technical achievement is the explicit construction of analytic, exact eigenfunctions, valid for arbitrary polynomial potentials and describing both bound and resonant quantum states.

Spectral Problem Definition

The primary object of paper is the spectral problem for the operator

$$H_N = \Lambda^N \left(\psi(x+\hbar) + \psi(x-\hbar) \right) + V_N(x)\psi(x) = E\psi(x),$$

with $V_N(x) = \sum_{k=0}^{N-1} (-1)^k h_k x^{N-k}$ and energy $E$. The nature of the spectral problem depends on the parity of $N$:

• Even $N$: $V_N(x)$ is confining, leading to a discrete spectrum of bound states. The operator is self-adjoint.
• Odd $N$: $V_N(x)$ is confining as $x\to+\infty$ but unbounded from below as $x\to-\infty$, resulting in resonances with complex energies.

A robust numerical treatment uses complex dilatation for $N$ odd to produce fast convergence for eigenstates that display power-law decay in one direction.

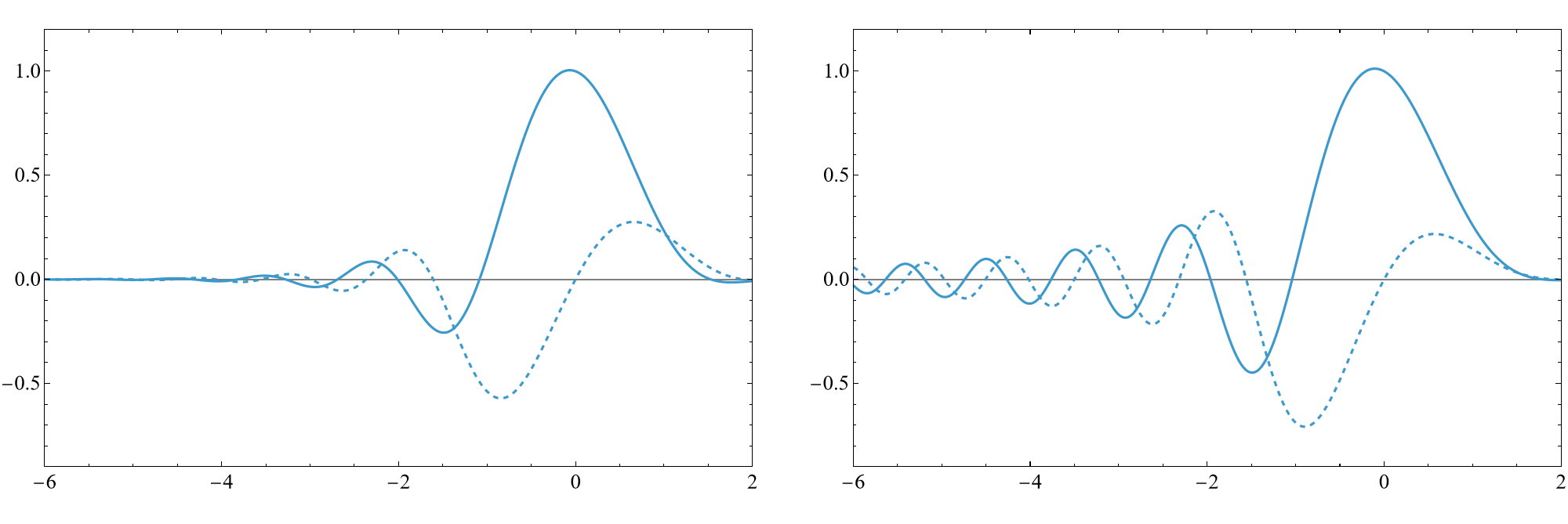
Figure 1: Numerical ground state eigenfunction ($E_0 \approx 0.54151 + 0.25905$) for $V_3(x)=x^3$, computed via complex dilatation.

Construction of Analytic Eigenfunctions

The analytic eigenfunctions are obtained using the open topological string/spectral theory (TS/ST) correspondence, leveraging explicit formulas for partition functions and instanton contributions from supersymmetric gauge theory. Key steps include:

• Use of Coulomb branch parameters $a_I$ via generalized Matone relations, replacing potential moduli $h_k$ with well-controlled gauge theory parameters.
• Explicit eigenfunction expressions involving Weyl group orbits, special defect partition functions $Z_D$, and additional entire functions $_n(x,\boldsymbol{a},\Lambda,\hbar)$ constructed to cancel singularities in $x$.

For $N$ even:

$$\psi_N^{\text{even}}(x,h) = Z_D(x,\boldsymbol{a},\Lambda,\hbar) \sum_{n \in \mathcal{W}_N \cdot \gamma} {}_n(x,\boldsymbol{a}) + \exp\left(\frac{2\pi x}{\hbar}\right)Z_D(-x,\mathbf{f}(\boldsymbol{a}),\Lambda,\hbar)\sum_{n \in \mathcal{W}_N \cdot (\gamma + e_N)} {}_n(-x,\mathbf{f}(\boldsymbol{a})).$$

For $N$ odd (resonant case):

$$\psi_N^{\text{odd}}(x,h) = Z_D(x,\boldsymbol{a},\Lambda,\hbar)\sum_{n \in \mathcal{W}_N \cdot \gamma} {}_n(x,\boldsymbol{a}) + \exp\left(\frac{\pi x}{\hbar}\right)Z_D(-x,\mathbf{f}(\boldsymbol{a}),\Lambda,\hbar)\sum_{n \in \mathcal{W}_N \cdot \gamma} {}_n(-x,\mathbf{f}(\boldsymbol{a})).$$

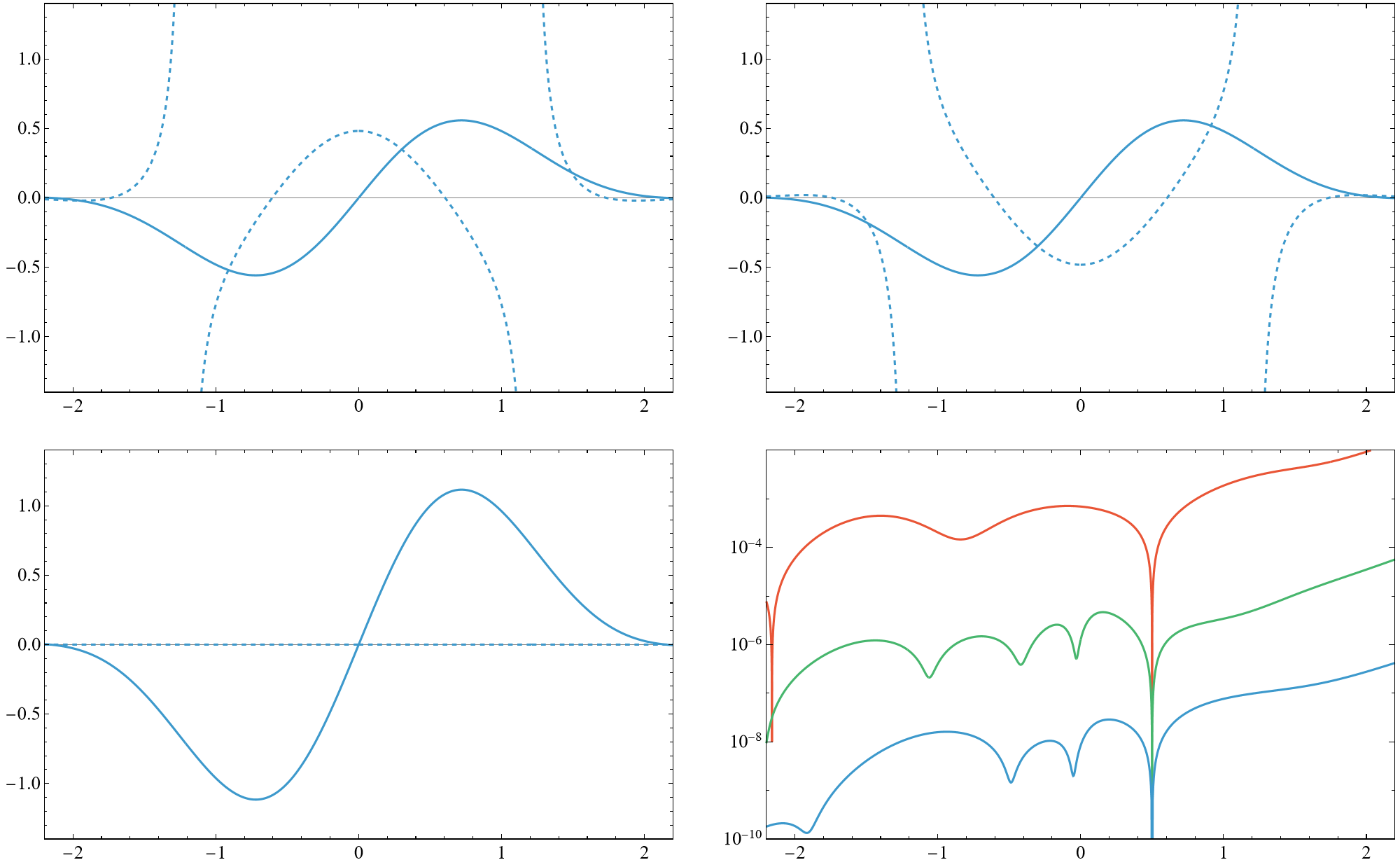
Crucially, individual saddle terms are non-entire, developing simple poles as functions of $x=a_I + k \hbar$, but their sum yields an entire solution for arbitrary $h_k$ (verified numerically for $N=2,3,4,5,6$ up to cubic order in $\Lambda$).

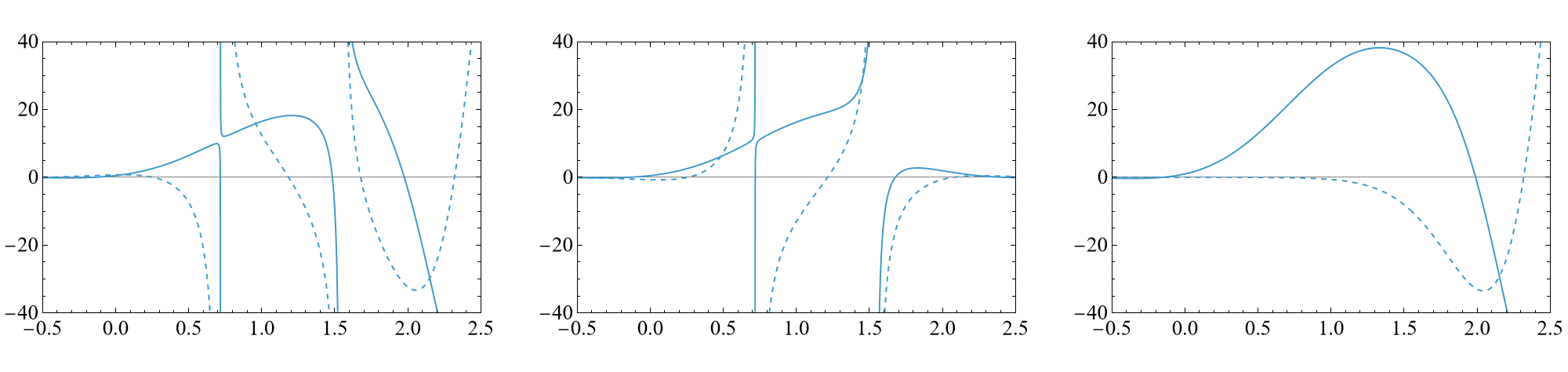
Figure 2: Off-shell eigenfunction for $V_3(x)$, $h_2 = -4$, $h_3 = -2.5$, showing the poles in single saddles and their cancellation in the full sum.

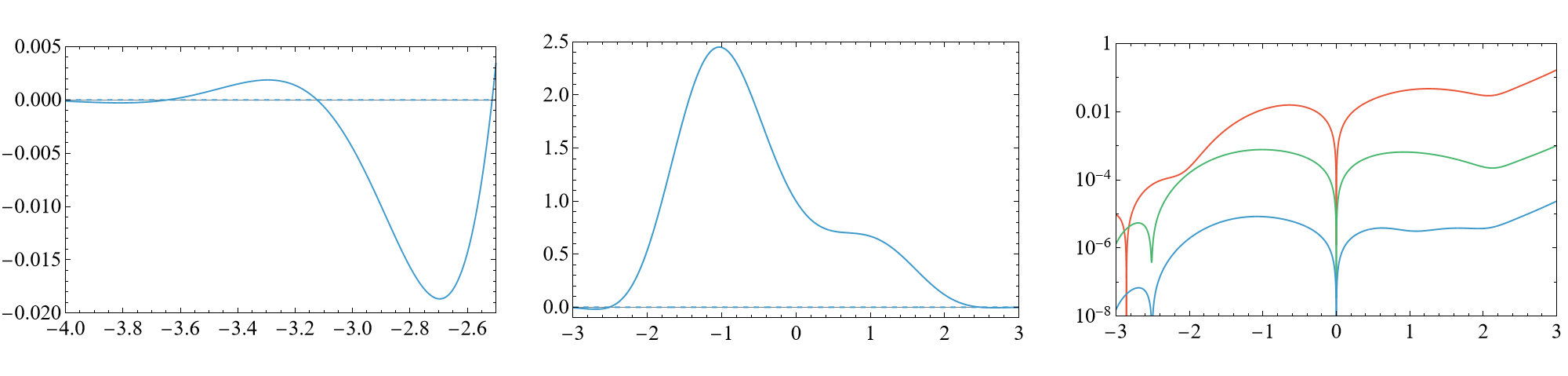
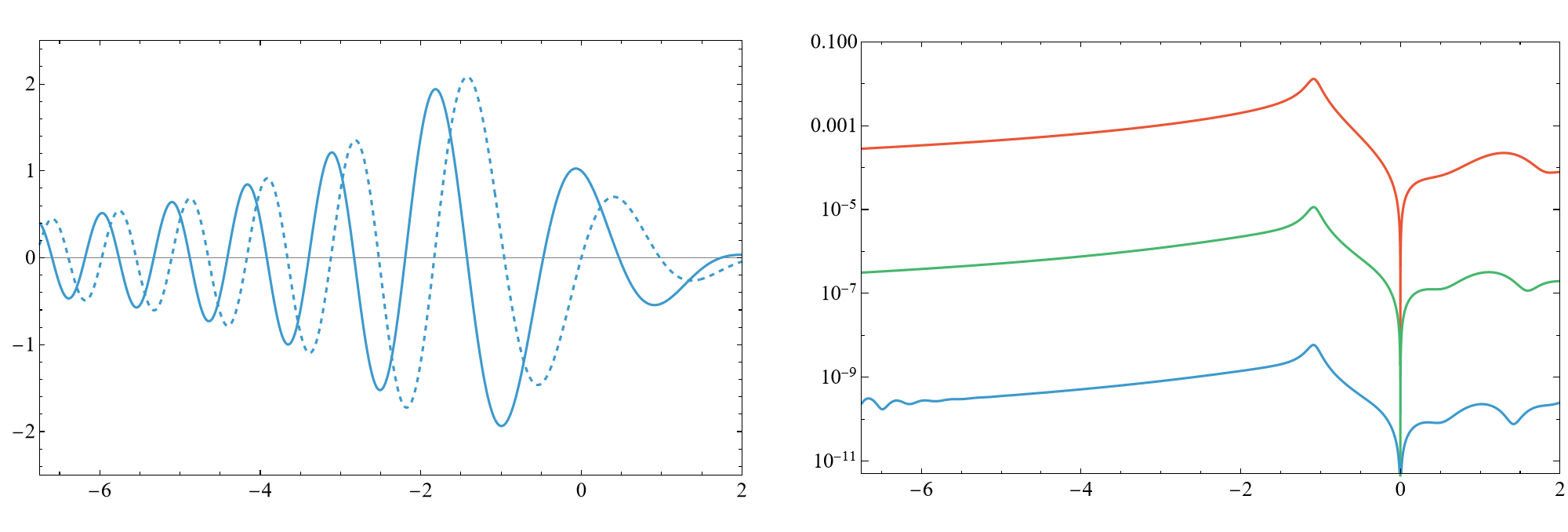
Figure 3: Ground state, $V_4(x)$, $h_2 = -3$, $h_3 = -0.1$, illustrating the failure of the oscillation theorem and excellent agreement with numerical diagonalization.

Quantization and Square Integrability

For generic energies, these analytic solutions are not $L^2$-normalizable. Square integrability is achieved at discrete energy values $E = E_k$, determined by an explicit quantization condition derived from the analytic structure of the eigenfunctions and the underlying Fredholm determinant:

• For $N$ even, the spectrum is purely discrete, as proved rigorously in [Laptev:2015loa].
• For $N$ odd, complex resonances arise, but real energies and enhanced decay occur at special loci in moduli space ("Toda points").

  Figure 4: Third excited state, $V_3(x)$ with $h_2 = 0$; colored curves show convergence as more terms in the $\Lambda$-expansion are included.

Algebraic and Geometric Insights

The spectral problem is closely related to integrable systems, specifically the Baxter equation for the closed quantum Toda lattice. The connection is manifest in the use of Weyl orbits, SU($N$) representations, and structure of the analytic eigenfunctions. In particular:

• Toda Points: Special values of $h_k$ ("Toda points") lead to spectral degeneracy and enhanced eigenfunction decay. At these points, all $h_k$ are quantized, matching the full set of quantization conditions from integrability theory.
• Oscillation Theorem Violation: The standard oscillation theorem fails generically; the $n$-th eigenfunction does not have exactly $n$ zeros, aside from the standard potentials. This anomaly is evident even in the symmetric quartic double well.

  Figure 5: First excited state of symmetric $V_4(x)$ with $h_2=3.5$, $h_3=0$, exhibiting cancellation of poles and agreement between analytic and numerical results.

Asymptotic Behavior and Physical Interpretation

Eigenfunctions exhibit unconventional asymptotics:

• For $N$ even, exponential decay at both infinities for on-shell states.
• For $N$ odd, exponential decay as $x\to+\infty$ and power-law decay (oscillatory) as $x\to-\infty$, characteristic of resonance states—yet still square-integrable.

Strong numerical agreement is observed between the constructed analytic solutions and numerical diagonalization in both asymptotic regimes and for intermediate values of $x$.

Figure 6: Ground state for $V_3(x)$ with $h_2=-5$, displaying precise match between analytic and numerically computed eigenfunctions.

Derivation from Open Topological String Theory

The construction of eigenfunctions is derived rigorously from the open TS/ST correspondence on toric $Y^{N,0}$ Calabi-Yau geometries. The difference operators arise as quantized mirror curves, with analytic solutions constructed from sums over root lattices and canonical modifications ensuring background-independence and analyticity for both open and closed moduli.

Implications and Future Directions

The established correspondence yields explicit analytic solutions for deformed Schrödinger-type operators, providing a rare solvable model for higher polynomial potentials. The analytic control offered by the TS/ST correspondence and gauge theory methods hints at broader applicability, including potentials with matter and more general gauge groups.

Key implications include:

• New families of quantum systems with exact spectral data for both bound and resonance states.
• Breakdown of textbook oscillation theorems in quantum difference equations, necessitating new mathematical frameworks.
• Enhanced spectral degeneracies and reality conditions for spectra at special moduli values, relevant for integrability theory and supersymmetric gauge theory.

Potential future developments include:

• Extension to matter-coupled Seiberg-Witten geometries.
• Deeper mathematical analysis of difference operators with unbounded potentials.
• Applications to quantum integrable systems and the paper of resurgence phenomena in non-perturbative quantum mechanics.

Conclusion

This work provides a complete analytic solution to the spectral problem of polynomially deformed difference Schrödinger operators arising from supersymmetric gauge theory quantization. Eigenfunctions can be constructed for arbitrary polynomial degrees, are explicit and entire in $x$, and are rigorously matched to numerical methods. The analysis uncovers new spectral phenomena, such as non-standard node distribution and enhanced degeneracies, and builds technical bridges between quantum mechanics, supersymmetric gauge theory, and topological string theory. The results invite extensive further exploration in both mathematical physics and integrable systems.