Work distribution and fluctuation theorem in AdS/CFT (2511.10305v1)

Abstract: From the AdS/CFT dictionary, we derive a bulk dual of the work distribution defined by the two-point measurement on the boundary, yielding a bulk formulation of the Tasaki-Crooks fluctuation theorem. We argue that this not only provides a holographic prescription of the work distribution, but is also expected to capture some "mesoscopic" aspects of quantum gravity.

• The paper establishes a holographic bulk prescription that translates boundary work distributions into gravitational path integrals and recovers the Tasaki–Crooks theorem.
• It employs the Schwinger–Keldysh formalism to map CFT work statistics to partition functions on bulk spacetime manifolds, demonstrated through a cyclic scalar field perturbation in AdS₃.
• The study links mesoscopic quantum gravity dynamics with thermodynamics by connecting boundary two-point measurements to bulk Brown–York energy fluctuations.

Work Distribution and Fluctuation Theorem in AdS/CFT

Introduction and Background

This work establishes a holographic bulk prescription for the work distribution and the Tasaki–Crooks fluctuation theorem (TCFT) in the context of AdS/CFT. The paper connects modern nonequilibrium quantum thermodynamics—specifically TPM-derived work statistics and fluctuation relations—to the gravitational sector via holography. The operational framework combines the statistical mechanics of mesoscopic systems with the emergent thermodynamics of gravitational backgrounds, motivated by extensive developments in black hole entropy, horizon thermodynamics, and generalized entropy in gravitational systems.

The key technical contributions involve (1) translating the boundary definition of the work distribution $p(W)$ and the associated characteristic function to bulk gravitational path integrals, and (2) verifying the Tasaki–Crooks theorem at leading perturbative order for a concrete bulk example, thus providing evidence of its utility in probing "mesoscopic" quantum gravity dynamics.

Quantum Work Distribution and Fluctuation Theorem: Boundary Definition

The Tasaki–Crooks theorem describes the relation between forward and reversed work distributions under a two-point measurement protocol for a quantum system with time-dependent Hamiltonian $H(t)$. One prepares an initial Gibbs state, applies a process protocol via $H(t)$, and defines work as the difference between final and initial projective measurement outcomes.

This leads to the work statistics: $$p(W) = \sum_{m,n} \delta(E_n^v - E_m^0 - W) p_{m\to n}$$ where $p_{m\to n}$ is the transition probability between energy eigenstates, and $U$ is the dynamical evolution operator. The characteristic function $G(u)$ is the Fourier transform: $$G(u) = \mathrm{Tr}\left[U e^{-i(u - i\beta) H(0)}U^\dagger e^{iu H(v)}\right]/Z(0)$$ Similarly, the reverse process yields $\tilde G(u)$.

The Tasaki–Crooks fluctuation theorem asserts: $\tilde p(-W) = e^{-\beta (W-\Delta F)}p(W)$ where $\Delta F$ is the free energy difference. Averaging over $p(W)$ yields the Jarzynski equality.

Bulk Prescription via AdS/CFT Dictionary

The translation of the work distribution into bulk variables leverages the Schwinger–Keldysh closed time path formalism. The characteristic functions $G(u)$ and $\tilde G(u)$ map to partition functions over bulk spacetimes $M$ and $\tilde M$, incorporating both Lorentzian and Euclidean segments glued together (Figure 1 & Figure 2). These manifolds encode the analytically continued boundary conditions and the time-dependent protocol.

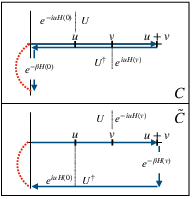
Figure 1: The closed time contours $C$ ($\tilde C$) for $G(u)$ ($\tilde G(u)$), indicating the Schwinger–Keldysh structure and periodic boundary conditions.

Specifically,

$$G(u) = e^{iS[\Phi; M]}/Z(0), \quad \tilde G(u) = e^{iS[\Phi; \tilde M]}/Z(v)$$

where $S$ is the bulk action, $\Phi$ collects bulk fields, and boundary conditions are set by the CFT protocol. The contour's structure encodes both "forward" and "backward" time evolution and the thermal initialization.

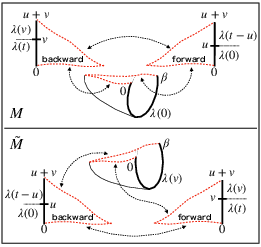
Figure 2: Bulk spacetime manifolds $M$ ($\tilde M$) required for path integral calculation of $G(u)$ ($\tilde G(u)$), illustrating Lorentzian evolution, Euclidean segments, and the potential for both black hole and horizonless saddle solutions.

This construction permits the explicit bulk calculation of $p(W)$ as a functional integral, with work statistics derived by solving the bulk equations of motion under appropriate boundary/junction conditions across the gluing surfaces defined by the Schwinger–Keldysh contour.

Interpretation of Bulk Work Statistics

The average work $\langle W \rangle$ on the CFT side corresponds to the expectation value change under unitary evolution. In the bulk, this maps to the change in Brown–York (BY) energy associated with dynamical evolution initiated from prescribed boundary conditions—effectively representing the energy influx into the bulk geometry corresponding to the protocol.

Unlike classical gravity, where deterministic evolution precludes a distribution over work due to fixed metric and BY energy, the full distribution $p(W)$ in the quantum regime reflects off-shell gravitational dynamics encoded in the path integral formalism. This suggests $p(W)$ measures quantum fluctuations in bulk energy resulting from boundary protocol, probing aspects of quantum gravity inaccessible through classical means.

Explicit Example: Scalar Field in AdS$_3$/CFT$_2$

To exemplify the formalism, the paper computes $p(W)$ for a cyclic scalar field perturbation in AdS$_3$—dual to a CFT$_2$ deformation. At leading order in a weak source, with the BTZ black hole background, the distribution is: $$p(W) = (1-q)\delta(W) + e^{\beta W/2}\;\frac{\pi(\Delta-1) r_+^{2\Delta-2}}{\Gamma(\Delta)\Gamma(\Delta+1)}\cdot\int\frac{dk}{(2\pi)^2} |\lambda_{W,k}\Gamma(\gamma_{W,k})\Gamma(\gamma_{W,-k})|^2$$ with $q$ the probability for nonzero work and $\lambda_{W,k}$ the protocol's Fourier coefficients. Verification reveals $\tilde p(W) = p(W)$ for this class of protocol, confirming the invariance under time-reversal in these circumstances. The average work matches independently calculated BY energy change from initial value problem evolution, indicating the operational connection between $p(W)$ and metric perturbations caused by time-dependent boundary conditions.

Implications, Extensions, and Future Directions

The holographic formulation of the work fluctuation theorem provides a novel avenue to analyze nonequilibrium processes in gravitational theories and potentially quantum gravity. The bulk prescription not only offers computational access to work statistics but also ties the underlying quantum fluctuations in bulk energy to measurable boundary protocols, bridging thermodynamic fluctuation relations with gravitational dynamics.

Several extensions are anticipated:

• Generalization to multitrace operator deformations, charged or spinning boundary operators, and strongly coupled initial states.
• Analysis of the relationship between boundary FTs, their bulk duals, and the emergence of various forms of the second law, especially in holographic composite or open systems.
• Implementation of Lindblad evolution and open system fluctuation relations in holography.
• Deeper investigation of the precise bulk process corresponding to boundary TPM, which may require further development of quantum gravitational path integral techniques.

The approach provides both a framework for practical evaluation of nonequilibrium energy fluctuations in holography and a conceptual bridge toward understanding quantum gravity's "mesoscopic" properties—those between microscopic quantum degrees and macroscopic thermodynamic behavior.

Conclusion

This paper constructs and verifies a holographic bulk dual for the Tasaki–Crooks fluctuation theorem, enabling calculation of work distribution and corresponding fluctuation relations directly in gravitational theories via AdS/CFT. The work connects nonequilibrium statistical mechanics to dynamical processes in quantum gravity and establishes $p(W)$ as a probe of quantum gravitational dynamics not captured by classical computations. This formalism offers prospective routes for exploring the quantum statistical properties of gravity and for formulating generalized fluctuation theorems beyond current semiclassical paradigms.