OUGS: Active View Selection via Object-aware Uncertainty Estimation in 3DGS (2511.09397v1)
Abstract: Recent advances in 3D Gaussian Splatting (3DGS) have achieved state-of-the-art results for novel view synthesis. However, efficiently capturing high-fidelity reconstructions of specific objects within complex scenes remains a significant challenge. A key limitation of existing active reconstruction methods is their reliance on scene-level uncertainty metrics, which are often biased by irrelevant background clutter and lead to inefficient view selection for object-centric tasks. We present OUGS, a novel framework that addresses this challenge with a more principled, physically-grounded uncertainty formulation for 3DGS. Our core innovation is to derive uncertainty directly from the explicit physical parameters of the 3D Gaussian primitives (e.g., position, scale, rotation). By propagating the covariance of these parameters through the rendering Jacobian, we establish a highly interpretable uncertainty model. This foundation allows us to then seamlessly integrate semantic segmentation masks to produce a targeted, object-aware uncertainty score that effectively disentangles the object from its environment. This allows for a more effective active view selection strategy that prioritizes views critical to improving object fidelity. Experimental evaluations on public datasets demonstrate that our approach significantly improves the efficiency of the 3DGS reconstruction process and achieves higher quality for targeted objects compared to existing state-of-the-art methods, while also serving as a robust uncertainty estimator for the global scene.
Sponsored by Paperpile, the PDF & BibTeX manager trusted by top AI labs.
Get 30 days freePaper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a single, actionable list of what remains uncertain or unexplored in the paper and where future work could concretely extend the method.
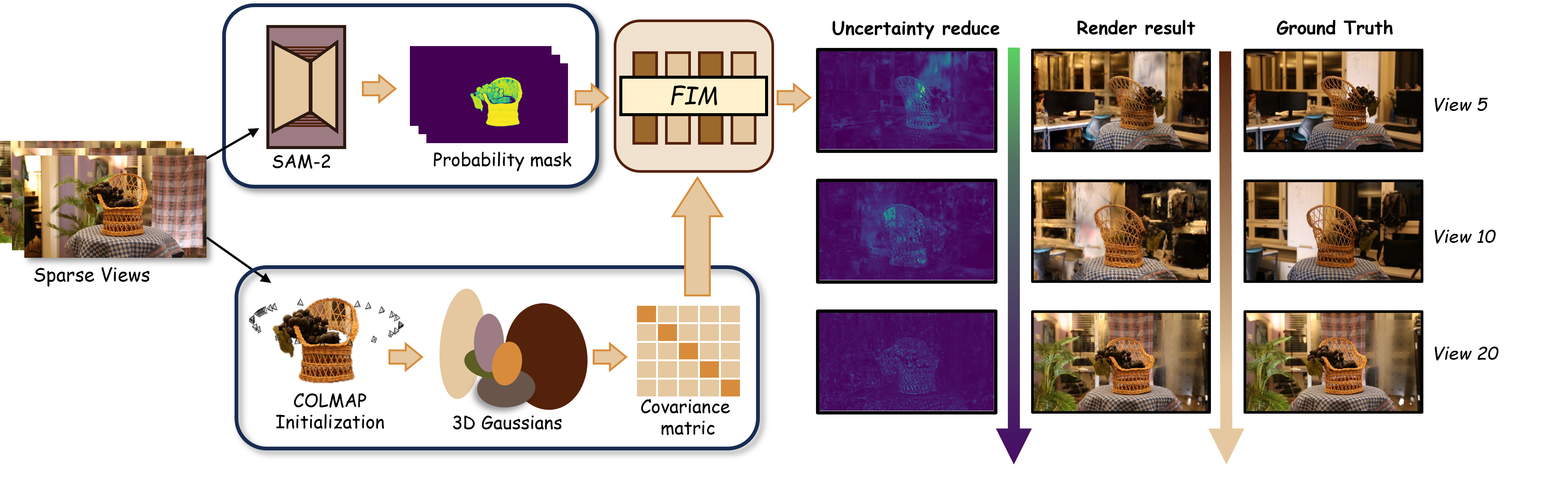
- Reliance on externally provided semantic masks (SAM‑2): no joint reconstruction–segmentation, no multi‑view consistency, no explicit handling of occlusions/partial visibility, and limited analysis under segmentation domain shift or severe mask noise/outliers.
- Single‑object focus: no formulation for multi‑object NBV with competing priorities, dynamic weighting, or fairness constraints; no paper of inter‑object trade‑offs in shared view budgets.
- Diagonal Fisher approximation: independence across parameters within and across Gaussians is assumed; missing structured correlations (e.g., position–opacity, neighboring Gaussians) and no evaluation of block‑diagonal/KFAC/Shampoo‑style alternatives versus compute overhead.
- First‑order uncertainty propagation (JΣJᵀ): no empirical analysis of breakdown regimes (e.g., highly nonlinear alpha compositing, saturated transmittance, sharp occlusion boundaries); second‑order or unscented approximations not benchmarked.
- Score design: the view score uses the sum of pixel‑wise trace(Σ); no comparison to alternative criteria (e.g., log‑determinant, largest eigenvalue, entropy, mutual information, or geometry‑biased weights) and their impact on NBV.
- Mask usage and uncertainty: masking is implemented as M(u)² scaling; mask uncertainty is not modeled or propagated, and alternative soft weighting schemes (e.g., calibration with mask reliability, boundary‑aware emphasis) are not explored.
- Geometry vs appearance decomposition: no experiments that separately score or weight geometric and appearance uncertainty to prioritize geometry early or adapt weighting over time.
- Calibration of predictive uncertainty: evaluation relies on AUSE only; no reliability diagrams, negative log‑likelihood, or expected calibration error; no separation of aleatoric vs epistemic components.
- Noise model and σ²: the Fisher–covariance link assumes a (homoscedastic) noise scale, but σ² is unspecified and uncalibrated; heteroscedastic image noise and HDR effects are not modeled.
- Computational profile: lack of runtime/memory analysis of Jacobian computation and Fisher updates for candidate views; scalability of per‑candidate uncertainty scoring with many Gaussians and large candidate sets is unquantified.
- Large‑scale scenes: beyond mentioning difficulty, there is no concrete strategy for memory/compute reduction (e.g., tiling, hierarchical LOD, on‑the‑fly pruning/merging, region‑of‑interest Jacobians).
- NBV planner myopia: the selection is greedy and per‑step; no look‑ahead/planning under motion/occlusion constraints, no trajectory or kinematic cost modeling, and no exploration–exploitation analysis.
- Candidate view space: the method selects from a discrete set of images; extension to continuous camera spaces, physical feasibility constraints, and real‑robot integration remain unaddressed.
- Stopping criteria: no uncertainty‑based termination rule or budget‑aware stopping condition beyond a fixed number of views.
- Robustness to pose/geometry initialization: sensitivity to COLMAP pose errors or poor Gaussian initialization is not analyzed; no closed‑loop pose refinement or uncertainty‑aware re‑localization.
- Dynamic or non‑Lambertian scenes: method assumes static scenes and SH‑based appearance; moving objects, specular/transparent materials, and lighting changes are not evaluated or explicitly modeled in uncertainty.
- Occlusion/visibility reasoning: uncertainty is not integrated with learned or geometric visibility priors; no explicit modeling of how candidate views disocclude high‑uncertainty regions.
- Hyperparameter sensitivity: aside from EMA momentum, key choices (λ regularization, SH order, σ², mask thresholding strategy, number of candidate views) lack sensitivity analyses.
- Fairness of object‑aware benchmarking: baselines that do not support masked scoring still evaluated with object‑only metrics; a standardized protocol for object‑centric NBV evaluation (metrics, masks, candidate sets) is not established.
- Geometry‑specific evaluation: despite geometric/appearance uncertainty decomposition, no geometry‑focused metrics (e.g., depth/normal/mesh error) are reported to validate geometric gains.
- Combining paradigms: integration of object‑aware Fisher with information‑theoretic selection (e.g., mutual information) or learned policies (RL/IL) is not investigated.
- Growth/pruning of Gaussians driven by uncertainty: no strategy to use uncertainty for adaptive Gaussian splitting, merging, or pruning during active acquisition.
- Online compute budget: no paper of how often to recompute Fisher/uncertainty, sub‑sampling pixels/Gaussians for fast surrogate scores, or anytime scoring under tight latency constraints.
Glossary
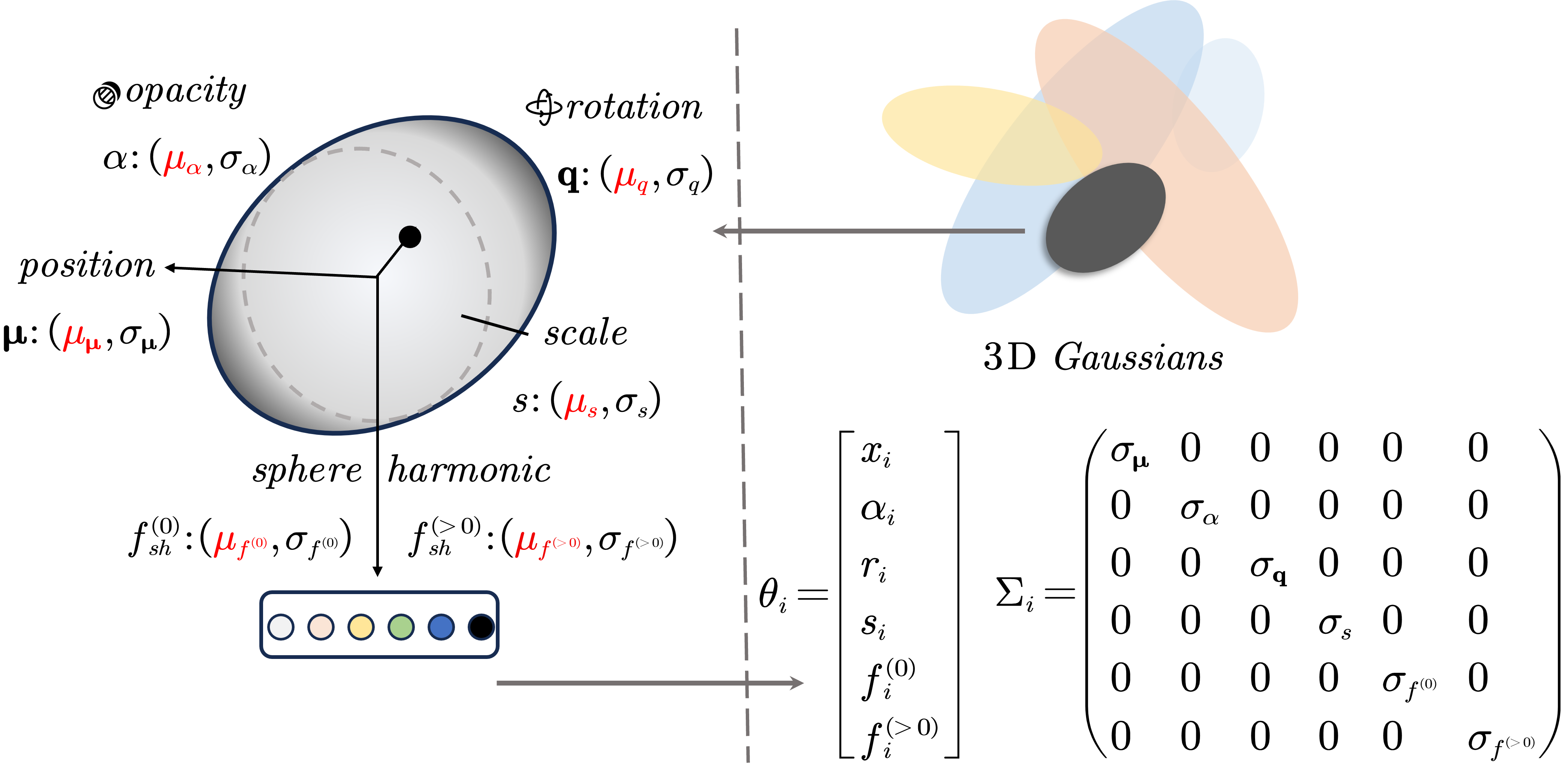
- 3D Gaussian Splatting (3DGS): An explicit scene representation using many 3D Gaussian primitives, enabling fast differentiable rendering. "Recent advances in 3D Gaussian Splatting (3DGS) have achieved state-of-the-art results for novel view synthesis."
- Alpha compositing: A standard image blending technique that accumulates colors and transparency along viewing rays. "Rendering in 3DGS uses a differentiable splatting approach based on standard alpha compositing."
- Anisotropic: Having direction-dependent properties; in 3DGS, Gaussians can scale differently along different axes. "represents a scene as a collection of anisotropic 3D Gaussian primitives"
- Area Under the Sparsification Error (AUSE): A metric that evaluates how well predicted uncertainty aligns with actual errors (lower is better). "The table reports the Area Under the Sparsification Error (AUSE), a rigorous metric for uncertainty quality (lower is better)."
- Block-diagonal matrix: A matrix composed of smaller square matrices along the diagonal, used to stack independent covariance blocks. "we stack the per-Gaussian covariances into a block-diagonal matrix"
- COLMAP: A structure-from-motion and multi-view stereo pipeline often used to initialize 3D scene geometry. "The 3D Gaussians are initialised with COLMAP"
- Covariance: A measure of joint variability among parameters; here propagated to pixel uncertainty via the Jacobian. "By propagating the covariance of these parameters through the rendering Jacobian"
- Differentiable rasterization pipeline: A rendering process whose outputs are differentiable with respect to scene parameters, enabling gradient-based optimization. "leveraging a fast, differentiable rasterization pipeline"
- Diagonal FIM approximation: An assumption that keeps only the Fisher Information Matrix’s diagonal entries to decouple parameters for efficiency. "we make a key simplifying assumption: we approximate the full FIM with its diagonal entries only"
- Exponential Moving Average (EMA): A smoothing method that updates statistics using exponentially decaying weights over time. "using an exponential moving average (EMA) of the squared gradients"
- Farthest-point strategy: A selection heuristic that chooses initial views that are maximally separated to improve coverage. "four initial views are selected using the farthest‑point strategy"
- Fisher Information Matrix (FIM): A matrix that quantifies how sensitive model predictions are to parameter changes; its inverse approximates parameter covariance. "inverse of the Fisher Information Matrix (FIM)"
- Fisher information gain: An information-theoretic criterion that measures expected improvement from acquiring a new view. "FisherRF proposes using Fisher information gain as a more principled metric."
- Frontier exploration: A planning strategy that prioritizes views on the boundary between known and unknown regions. "select views based on metrics like Shannon entropy or frontier exploration"
- Hessian-based metric: A second-derivative-based sensitivity measure used to quantify and prune uncertain Gaussians. "uses a Hessian-based metric to prune Gaussians with high uncertainty."
- Hierarchical Bayesian priors: Structured prior distributions over parameters that capture multi-level uncertainty. "use hierarchical Bayesian priors"
- Jacobian: The matrix of first-order partial derivatives mapping parameter perturbations to changes in rendered pixel colors. "through the rendering Jacobian"
- LPIPS: A learned perceptual image similarity metric used to evaluate visual quality. "Hence, we apply PSNR, SSIM, and LPIPS to evaluate the result."
- Maximum a posteriori (MAP) estimate: The parameter values that maximize the posterior probability given data and priors. "θ⋆ is the MAP estimate after optimization."
- Mutual information: A measure of shared information between variables; used to select views that most reduce uncertainty. "selects views that maximize mutual information."
- Neural Radiance Fields (NeRF): An implicit volumetric representation that synthesizes views by learning radiance and density fields. "The advent of Neural Radiance Fields (NeRF) marked a breakthrough"
- Neural Visibility Fields: Models that predict which scene regions are visible from a viewpoint to guide view planning. "Neural Visibility Fields learn to predict which parts of a scene are visible from a given viewpoint"
- Next-Best-View (NBV) planning: The process of selecting the next camera viewpoint to maximally improve reconstruction. "Active view selection, or Next-Best-View (NBV) planning, is a long-standing problem in computer vision and robotics"
- Occupancy maps: Grids that encode free, occupied, or unknown space, commonly used in robotic exploration. "maximize the exploration of unknown free space using occupancy maps."
- Opacity: A scalar controlling a Gaussian’s transparency contribution in compositing. "A scalar opacity value "
- Parallax: Apparent displacement of scene features due to viewpoint changes; important for depth reasoning. "characterised by long-baseline parallax and strong depth discontinuities."
- PSNR: Peak Signal-to-Noise Ratio, a fidelity metric for reconstructed images. "Hence, we apply PSNR, SSIM, and LPIPS to evaluate the result."
- Quaternion: A four-dimensional representation of 3D rotation used for Gaussian orientation. "an orientation quaternion ."
- SAM2: A segmentation model used to obtain object masks for object-aware uncertainty. "object masks are obtained from SAM2"
- Semantic probabilities: Class-likelihoods per pixel used to weight an object’s soft mask. "a soft mask based on semantic probabilities."
- Shannon entropy: An information measure used to evaluate uncertainty or information content in view selection. "select views based on metrics like Shannon entropy or frontier exploration"
- Soft mask: A probabilistic per-pixel weighting in [0,1] that isolates an object in uncertainty estimation. "we introduce a soft mask based on semantic probabilities."
- Spatial Uncertainty Field: An auxiliary learned field that predicts uncertainty across space. "adds a Spatial Uncertainty Field for sparse inputs"
- Spherical Harmonics (SH): A basis for representing view-dependent color on the sphere via low-order coefficients. "view-dependent color modeled by Spherical Harmonics (SH)."
- Splatting: A rendering technique that projects and blends primitives (Gaussians) onto the image plane. "Rendering in 3DGS uses a differentiable splatting approach"
- SSIM: Structural Similarity Index Measure, a perceptual metric for image quality. "Hence, we apply PSNR, SSIM, and LPIPS to evaluate the result."
- Variational inference: A method to approximate complex posteriors by optimizing a tractable family of distributions. "employ variational inference."
- Voxel-grid representations: Discrete volumetric grids used to model and plan in 3D environments. "voxel-grid representations and select views based on metrics like Shannon entropy or frontier exploration"
Collections
Sign up for free to add this paper to one or more collections.