The Dark Energy Survey Supernova Program: A Reanalysis Of Cosmology Results And Evidence For Evolving Dark Energy With An Updated Type Ia Supernova Calibration
Abstract: We present improved cosmological constraints from a re-analysis of the Dark Energy Survey (DES) 5-year sample of Type Ia supernovae (DES-SN5YR). This re-analysis includes an improved photometric cross-calibration, recent white dwarf observations to cross-calibrate between DES and low redshift surveys, retraining the SALT3 light curve model and fixing a numerical approximation in the host galaxy colour law. Our fully recalibrated sample, which we call DES-Dovekie, comprises $\sim$1600 likely Type Ia SNe from DES and $\sim$200 low-redshift SNe from other surveys. With DES-Dovekie, we obtain $Ω{\rm m} = 0.330 \pm 0.015$ in Flat $Λ$CDM which changes $Ω{\rm m}$ by $-0.022$ compared to DES-SN5YR. Combining DES-Dovekie with CMB data from Planck, ACT and SPT and the DESI DR2 measurements in a Flat $w_0 w_a$CDM cosmology, we find $w_0 = -0.803 \pm 0.054$, $w_a = -0.72 \pm 0.21$. Our results hold a significance of $3.2σ$, reduced from $4.2σ$ for DES-SN5YR, to reject the null hypothesis that the data are compatible with the cosmological constant. This significance is equivalent to a Bayesian model preference odds of approximately 5:1 in favour of the Flat $w_0 w_a$CDM model. Using generally accepted thresholds for model preference, our updated data exhibits only a weak preference for evolving dark energy.
Summary
- The paper recalibrates the DES SN Ia dataset using updated photometry and SALT3 modeling to reduce systematic errors.
- Improved zero-point calibration with DA white dwarfs and Gaia SEDs refines distance measurements and minimizes cross-survey biases.
- Evidence for a time-evolving dark energy equation of state is weakened, aligning cosmological constraints more closely with ΛCDM.
Recalibration of the Dark Energy Survey Supernova Program: Cosmological Impact and Evidence for Evolving Dark Energy
Introduction and Motivation
The Dark Energy Survey Supernova Program (DES-SN) has been foundational in providing large, homogeneous samples of Type Ia supernovae (SNe Ia), critical for precision cosmology through distance-redshift measurements. This study presents a full reanalysis of the DES 5-year SN Ia cosmology results, introducing an updated, physically-motivated calibration for cross-survey photometry, improved modeling in the SALT3 framework, and corrections to the color law implementation. The recalibrated sample, termed DES-Dovekie, contains 1600 DES SNe Ia and 200 low- SNe from other surveys, and addresses key systematic errors—particularly in photometric calibration—that can mimic or obscure cosmological signals such as time evolution in the dark energy equation of state.
Photometric Cross-Calibration and Improvements
Calibration Advances
DES-Dovekie incorporates a revised photometric cross-calibration exploiting new DA white dwarf spectra, expanded usage of the Gaia SED standards, and refined error modeling in the cross-survey zero-points and filter functions. This is visually summarized in the zeropoint offset comparison across calibration approaches:
Figure 1: Calibration offsets for DES, CfA3S, CfA3K, CSP, and Foundation filters at the surveys' median redshifts; the improvement in DES calibration precision is highlighted by reduced uncertainty with the DA WD reference.
The recalibration leads to non-negligible shifts in the relative zeropoints, notably for the DES sample, providing improved control of relative distances across redshift and survey.
Light Curve Modeling and Color Law
SALT3 was retrained on the recalibrated dataset, excising problematic low- data as warranted by the improved calibration, and the implementation of the Fitzpatrick (1999) color law was upgraded from a polynomial approximation to an exact formula. This correction ensures consistency between dust extinction modeling in simulation and lightcurve fitting, crucial for accurate bias corrections—especially when simulating populations with a wide range.
Data Selection and Sample Characterization
The DES-Dovekie sample is constructed using stringent quality and host association criteria on the original DES-SN5YR transient database; events passing these criteria align closely in parameter distribution to the previous release except for a small offset in the mean color among DES events, explained by calibration-induced shifts rather than sample composition.
Figure 2: Distributions of comparing DES-SN5YR and DES-Dovekie samples, indicating primary shifts only in the DES SN color distribution.
Simulations of the recast sample using the updated SALT3/Dovekie calibration confirm robust agreement in redshift, stretch, and color distributions between data and model:
Figure 3: Simulated versus observed statistical distributions for key SN parameters, showing excellent correspondence and supporting unbiased cosmological inference.
Systematic Error Budget
A principal result of this work is a rigorous, fully-propagated systematic error budget for cosmological inference from SNe Ia. The uncertainties on and arise from calibration/modeling, SN astrophysics (e.g., host-galaxy correlations, intrinsic scatter), Milky Way extinction, survey selection, classification contamination, and redshift uncertainties.
Figure 4: Systematic and statistical error contributions to in Flat CDM from SNe Ia alone.
Figure 5: Systematic and statistical uncertainties on in Flat CDM with and without CMB priors, revealing dominant contributions from SN properties and calibration/modeling.
Calibration/modeling uncertainties have increased relative to the previous release, largely due to a correction in weighting the photometric systematics, but this rectifies a documented underestimation in prior work. Astrophysical systematics, particularly from host-galaxy dust models, remain a leading source of uncertainty.
Figure 6: Median binned differences in SN Ia distance modulus for the nine calibration systematic realizations, showing lack of significant redshift-dependent trends.
Survey modeling and photometric classification systematics are shown to be subdominant; possible biases from galaxy catalog depth (Figure 7, left) and redshift-efficiency modeling (Figure 7, right) produce negligible effects on distance measurements.
Figure 7: The left panel shows no significant distance bias from changing the galaxy catalog; the right panel indicates negligible impact from altering spectroscopic redshift efficiencies.
Cosmological Constraints and Model Selection
Flat CDM Results
With the recalibrated SN sample, the matter density in Flat CDM is measured with SNe alone as . When combined with the Planck+ACT+SPT CMB and DESI BAO data, the constraint sharpens to , in good agreement with external probes.
Figure 8: Constraints on for Flat CDM from DES-Dovekie (blue), Planck CMB (grey), DESI BAO (black), and their combination (dark blue).
Extensions to CDM and Time-Evolving Dark Energy
Weak evidence is found for evolving dark energy:
- In Flat CDM, joint constraints yield , .
- The frequentist improvement in fit versus Flat CDM is (equivalent to ), but Bayesian model preference (Δlogℤ = -1.7) only mildly supports the time-varying model, corresponding to odds of 5:1.
This preference is substantially weaker than prior DES analyses, which reported up to significance. The recalibrated distances reduce the relative dimness of low- SN Ia compared to mid- objects, but leave the cosmological inferences internally consistent and more robust to cross-survey calibration concerns.
Implications and Theoretical Interpretation
Systematics and Calibration Robustness
This study demonstrates that meticulous calibration—including the inclusion of DA white dwarf standards and corrected color law implementations—significantly mitigates artefactual signals that can masquerade as evolving dark energy. The observed reduction in evidence for time variation in arises from improved control of low-to-high redshift photometric systematics rather than statistical fluctuations or sample composition.
Remaining Systematic Uncertainties
Astrophysical systematics, particularly those related to dust and host-galaxy properties, remain non-trivial. The presented analysis sets a benchmark for future SN cosmology studies, emphasizing transparent, reproducible calibration transfer and systematic quantification. Ongoing and future low- SN surveys, as well as cross-comparison with alternative standardization schemes (e.g., hierarchical Bayesian models), will be necessary to further constrain residual systematics.
Model Selection, Hubble Tension, and Future Prospects
No strong statistical evidence for is found when using current state-of-the-art calibration and joint analysis with CMB and BAO. The analysis solidifies the lack of a cosmographically-driven resolution to the Hubble tension within standard extensions to dark energy. The improved internal cross-consistency demonstrated here should serve as a model for LSST and future large SN surveys.
Conclusion
The recalibrated DES-Dovekie SN Ia data provide the most systematic-error controlled distance-redshift sample to date for cosmological inference. The updated calibration, revised SALT3 model, and accurate color law implementation collectively reduce the previously reported evidence for time-varying dark energy to "weak" in model-preference parlance. The matrix of systematics presented here demonstrates that further progress toward sub-percent constraints on dark energy properties will require improvements both in photometric calibration (ideally with new, independently calibrated low- samples) and in the astrophysical modeling of SN Ia environments. Future advancements in deeply cross-calibrated, multi-survey SN Ia samples and expanded astrophysical modeling are essential for next-generation cosmological measurements.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
What this paper is about (simple overview)
Scientists use special exploding stars called Type Ia supernovae as “standard candles” to measure how far away galaxies are. This helps them figure out how the universe is expanding and what “dark energy” is doing. This paper re-checks (reanalyses) five years of supernova data from the Dark Energy Survey (DES), using better “calibration” and updated tools. The goal is to see whether the earlier hints that dark energy might be changing over time still hold up.
The main questions the paper asks
- Did small measurement tweaks (calibration updates and model fixes) change what we think about dark energy?
- How do the improved supernova distances affect the basic ingredients of the universe (like how much matter there is)?
- When we combine these supernova results with other big datasets (like the cosmic microwave background and galaxy maps), do we still see signs that dark energy is evolving over time?
How the researchers did it (in everyday language)
Think of this project like double-checking a huge set of measurements with better rulers and a cleaned-up instruction manual.
- Calibrating the “rulers”: Different telescopes and surveys measure brightness slightly differently, a bit like different rulers being off by a millimeter. The team carefully cross-checked and aligned these “rulers” using very well-understood stars, including white dwarfs (which act like reliable “standard lamps”), and data from Gaia and the Hubble Space Telescope. This step is called “cross-calibration.”
- Updating the supernova model: They retrained a widely used model called SALT3 (you can think of it like a recipe that turns a supernova’s changing brightness and color over time into a distance). The new training uses the improved calibration so distances come out more accurate.
- Fixing a dust formula: Light from supernovae passes through dust, which acts like tinted sunglasses—making light dimmer and redder. The team found and fixed a small mathematical shortcut in how the dust effect was calculated, especially important for the fake (simulated) data used to correct biases.
- Correcting for “selection bias”: Brighter or bluer supernovae are easier to spot, so your sample can be skewed. The team ran many realistic simulations to understand and correct for these effects, ensuring the final distances aren’t biased.
- Handling impostors: Not every explosion in the sky is a Type Ia supernova. They used machine learning to estimate, for each event, the chance that it’s really a Type Ia, and they accounted for the small fraction that aren’t.
- Combining with other evidence: They compared the DES supernova distances with two other powerful clues:
- The cosmic microwave background (very ancient light from the early universe) from Planck, ACT, and SPT.
- Galaxy “sound waves” called BAO from DESI (these measure how fast the universe has expanded over time).
What they found and why it matters
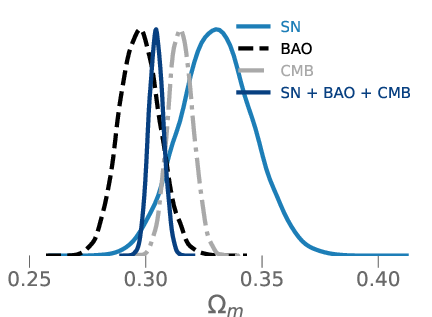
- A small but important shift in matter content: Using their newly calibrated supernova sample (they call it DES-Dovekie), they find the matter fraction of the universe is Ωm = 0.330 ± 0.015 in a flat universe with a cosmological constant (the usual ΛCDM model). This is a modest change (down by 0.022) from the earlier DES-SN5YR result, driven by better calibration.
- Weaker evidence that dark energy changes over time: When DES-Dovekie supernovae are combined with CMB and DESI BAO data, the best-fit dark energy parameters are w0 = −0.803 ± 0.054 and wa = −0.72 ± 0.21 (these numbers describe how dark energy might change with time). This combination still prefers “evolving dark energy” over a simple cosmological constant (w = −1), but the strength of the evidence drops from about 4.2σ to 3.2σ. In everyday terms:
- Before: stronger hint that dark energy changes with time.
- Now: the hint is weaker—only a “weak preference” by common standards (about 5:1 odds in Bayesian terms).
- Calibration really matters: A few hundredths of a magnitude (a tiny change in brightness) can shift cosmology results. By improving the cross-calibration and fixing a small dust-law approximation, some of the earlier tension eased.
- Internal checks passed: Simulations matched the real data well, and when they tested the full pipeline on fake universes, it successfully recovered the right answers. That gives confidence the analysis is sound.
What this means going forward
- Dark energy might still be evolving, but the evidence is not strong yet. With the improved measurements, the case is more cautious than before.
- Tiny measurement details can have big effects. This work shows that careful calibration—making sure all the “rulers” agree—is crucial. As future surveys (like Rubin Observatory and NASA’s Roman mission) bring even more supernovae, getting these details right will be essential.
- The updated tools and open pipeline will help the community double-check and build on these results. That’s how we’ll pin down whether dark energy is truly changing or if the universe is still well described by a simple cosmological constant.
In short
The team remeasured supernova distances with better calibration and a fixed model, then combined them with other top datasets. The result: the universe likely has about one-third matter, and while there’s still a hint that dark energy changes over time, it’s weaker than before. More and even better data will be needed to make a firm call.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a focused list of what remains missing, uncertain, or unexplored in the paper, framed as concrete items future researchers can act on.
Calibration and photometry
- Quantify residual inter-survey zero-point and bandpass uncertainties after Dovekie, including correlated errors across filters and surveys; publish end-to-end propagation into distances and cosmology.
- Validate cross-calibration independently (e.g., HST CALSPEC spectrophotometric standards, overlapping fields, cross-observed SNe across surveys) to demonstrate the ≤0.01 mag requirement is met across the full redshift range.
- Propagate uncertainties from DA white dwarf atmosphere models and Gaia spectrophotometric calibration into SN distances and the systematic covariance.
- Assess the impact of not reprocessing low‑z photometry (e.g., consistent scene modeling, chromatic corrections, DCR) on relative calibration and colors; test remeasuring low‑z fluxes with a uniform pipeline.
- Revisit filter transmission functions and shifts (PS1, CfA, CSP) with independent measurements; quantify sensitivity of μ(z) to remaining bandpass errors.
Light-curve modeling and standardization
- Test the sensitivity of cosmology to SALT3.DOV training choices: training sample selection, wavelength coverage, basis flexibility, and error model; compare to alternative models (e.g., SNEMO, SUGAR, BayeSN).
- Investigate potential circularity: calibration used in SALT training influences fitted colors and bias corrections; quantify iteration stability and convergence.
- Explicitly model intrinsic scatter components (coherent vs chromatic; dependence on color/stretch/host) and quantify their effect on β, μ, and w0–wa.
- Probe nonlinearity or breaks in the color–luminosity relation (β), and any redshift dependence; assess whether such effects mimic evolving dark energy.
- Evaluate robustness of distances to the choice of dust/extinction law: vary F99 vs CCM/OD94 and host dust parameter distributions; quantify the cosmology shift.
- Quantify the impact of the fixed F99 implementation on fitted color, β, and μ beyond simulations, especially in regimes with significant host extinction.
Bias corrections, selection, and classification
- Stress-test BBC bias corrections: dependence on the 4D binning scheme, grid resolution, and simulation realism (detection pipeline, cadence, observing conditions); compare against forward-modeling approaches or hierarchical analyses.
- Audit the ∼100 SNe that differ between DES-Dovekie and DES-SN5YR (inclusions/exclusions), and quantify how these changes affect μ and cosmology.
- Assess cosmology sensitivity to the σx1 cut change and to the SNN classification threshold (P_Ia); explore continuous probability weighting vs hard cuts.
- Calibrate SNN probabilities with spectroscopically confirmed subsamples; quantify residual non‑Ia contamination vs redshift and its cosmology impact; repeat with SCONE and SNIRF to bound classifier systematics.
- Quantify selection bias from excluding hostless SNe (d_DLR>4), including effects on redshift, color, and host property distributions.
Host galaxy effects
- Test evolution and functional form of the “mass step” (γ): redshift dependence, continuous dependence on M*, sSFR, or rest‑frame u−r; report cosmology sensitivity to these choices.
- Evaluate robustness of host galaxy mass estimates (PEGASE2/Kroupa) by comparing to alternative SED‑fitting codes (e.g., Prospector, CIGALE) and propagate mass uncertainties into γ and μ.
- Model host dust law evolution (R_V, A_V) with environment/redshift and its interplay with color and β; quantify impacts on bias corrections and w0–wa.
Cosmological modeling and external data combinations
- Perform explicit analyses allowing curvature (Ω_k≠0) for both ΛCDM and w0–wa CDM, and quantify how Ω_k freedom changes model preference for evolving dark energy.
- Systematically vary Bayesian priors (e.g., Ω_m upper bound, w0 range, w0+wa constraint, Σmν) and report impacts on parameter posteriors and evidence; assess prior‑driven shifts.
- Quantify dependence on CMB likelihood choices: full Planck vs Planck‑lite, ACT/SPT calibration priors, lensing amplitudes; evaluate potential overlap‑induced correlations rather than assuming they are negligible.
- Assess BAO dataset dependence: compare DESI DR2 to DES photometric BAO and SDSS BAO; report consistency and stability of w0–wa constraints across BAO choices.
- Test sensitivity to peculiar velocity modeling (velocity dispersion, flow models, heliocentric vs CMB-frame transforms) on low‑z distances and cosmology.
- Decompose the evolving dark energy preference by probe: perform leave‑one‑out analyses (SNe-only, BAO-only, CMB-only, and combinations) and apply tension metrics to pinpoint drivers.
Systematics covariance and reproducibility
- Expand and publish the full systematic covariance components (calibration, dust law, classification, selection, bandpass shifts, photometric errors, redshift/pv errors), including realistic inter‑systematic correlations.
- Cross‑validate Bayesian evidence (ΔlogZ) with multiple samplers (e.g., MultiNest, PolyChord) and report variance due to sampler settings; provide uncertainty estimates beyond a single 0.2 value.
- Provide versioned, open artifacts (SALT3.DOV training inputs and outputs, calibration surfaces, biasCor simulations, classification models, cosmology configs) to enable independent, bit‑for‑bit replication.
Residuals and diagnostics
- Examine Hubble residual correlations with SN parameters (x1, c), host properties (M*, u−r), sky position, and observing conditions; identify unmodeled trends.
- Investigate the source and consequences of the DES color distribution mean shift (Δc≈−0.014): disentangle calibration vs training demographics; quantify its effect on β and μ.
- Report and model the remaining Hubble diagram scatter (RMS≈0.169): partition into measurement vs intrinsic components, and test if scatter depends on SN or host properties.
Practical Applications
Immediate Applications
Below are actionable use cases that leverage the paper’s findings, improved methods, and open pipeline components and can be deployed now, subject to noted assumptions and dependencies.
- Cross-survey photometric calibration workflow for precision astronomy
- Sectors: academia (astronomy, cosmology), instrumentation, software
- Use case: apply the Dovekie cross-calibration (DA white dwarf standards, Gaia spectroscopy, PS1 interstitial reference) to recalibrate existing and ongoing supernova and galaxy surveys to achieve ~0.01 mag relative accuracy across redshift and instruments.
- Tools/products/workflows: Dovekie calibration solution; updated filter transmission shifts; DA white dwarf spectral models; Gaia spectral integration; Pan-STARRS interstitial approach; improved zero points and uncertainty model.
- Assumptions/dependencies: access to calibrator catalogs (Gaia, HST, SDSS, PS1) and instrument passbands; adoption of exact F99 color law; consistent application of chromatic/atmospheric corrections; instrument teams willing to update passband models.
- End-to-end reproducible SN cosmology pipeline for reanalysis and validation
- Sectors: academia (cosmology), research software engineering
- Use case: re-run and stress-test published SN cosmology results with the updated pipeline (SALT3.DOV, correct calibration weights, fixed color law, regenerated bias corrections) to quantify systematics and cross-check claims of evolving dark energy across data releases.
- Tools/products/workflows: SNANA (with exact Fitzpatrick 99 color law); SALT3.DOV; BBC (BEAMS with Bias Corrections); PIPPIN orchestration; Cosmosis + Nautilus sampler; Planck-py, ACT-DR6-Lite, candl likelihoods; improved interface to DES-SN5YR pipeline.
- Assumptions/dependencies: computational resources for nested sampling; availability of public likelihoods and survey inputs; stable priors; trained personnel in using the software stack.
- Photometric-only supernova classification and contamination-aware inference
- Sectors: academia (astronomy, ML), software/AI
- Use case: use SuperNNova (and alternatives) plus BEAMS mixture modeling to perform cosmology with photometrically classified SN Ia samples while rigorously down-weighting non-Ia contamination via probability-aware likelihoods.
- Tools/products/workflows: SuperNNova; SCONE; SNIRF; BEAMS framework; updated Dust2Dust population model; 4D cell bias corrections in {z, c, x1, log10(M⋆)}.
- Assumptions/dependencies: realistic simulations for training and bias correction; robust host-galaxy redshifts; monitoring of classifier domain shift across surveys.
- Adoption of exact Fitzpatrick (1999) color law and atmospheric chromatic corrections in imaging pipelines
- Sectors: academia (imaging surveys), instrumentation; industry (remote sensing, earth observation)
- Use case: implement exact F99 color law and refine differential chromatic refraction (DCR) corrections to reduce bias in color-dependent photometry and derived distances or reflectances.
- Tools/products/workflows: updated SNANA color law implementation; chromatic/DCR correction modules; validated passband models.
- Assumptions/dependencies: accurate source SEDs or spectral proxies; well-characterized filter profiles; sufficient calibration observations across airmass and color.
- Host-galaxy property modeling to reduce residuals (mass step, u–r color)
- Sectors: academia (astronomy), data science
- Use case: integrate host-galaxy mass and rest-frame color into standardization to reduce residual scatter and systematic offsets (“mass step” correction).
- Tools/products/workflows: uniform host SED fitting pipeline (PEGASE2 + Kroupa IMF); cross-survey host photometry ingestion (uJHK, GALEX UV).
- Assumptions/dependencies: consistent host photometry across surveys; reliable mass/color estimation across redshift; separation of host-driven and intrinsic SN color/luminosity effects.
- Education and training in uncertainty quantification and model preference
- Sectors: education, academia
- Use case: course modules and labs that teach mixture modeling (BEAMS), bias corrections via simulations (BBC), frequentist vs Bayesian model preference (Wilks vs evidence), and reproducible cosmology workflows.
- Tools/products/workflows: public DES-SN5YR/DES-Dovekie pipeline; Cosmosis + Nautilus; Planck/ACT/SPT likelihoods; demo notebooks.
- Assumptions/dependencies: open access to data and code; instructors familiar with the software stack; manageable compute for classroom-scale runs.
Long-Term Applications
Below are applications that require further research, scale-up, or community adoption before being broadly feasible.
- Millimagnitude-level global cross-calibration across next-generation surveys (Rubin LSST, Roman, Euclid)
- Sectors: academia (astronomy/cosmology), instrumentation, standards
- Use case: institutionalize Dovekie-like cross-calibration (DA white dwarfs, Gaia spectra, overlapping interstitial surveys) to unify photometric systems across multiple telescopes and epochs, enabling robust cosmology and precision time-domain astrophysics.
- Tools/products/workflows: standardized spectral standard catalogs; cross-survey calibration-as-a-service; routine passband monitoring and updates; unified calibration uncertainty budgets.
- Assumptions/dependencies: long-term stewardship of calibration catalogs; coordinated survey operations; stable instrument characterization; agreement on standards and governance.
- Strengthened constraints (or refutation) of evolving dark energy
- Sectors: academia (cosmology), policy (prioritization of survey resources)
- Use case: integrate larger SN samples with improved calibration and multi-probe analyses (BAO, CMB lensing) to clarify whether the weak preference for evolving dark energy persists, diminishes, or strengthens.
- Tools/products/workflows: expanded SN samples from LSST/Roman; refined systematic covariance modeling; multi-probe inference platforms; improved prior setting based on astrophysical bounds.
- Assumptions/dependencies: control of cross-survey systematics to ≲0.01 mag; multi-probe consistency; improved modeling of dust, selection, and host effects.
- Generalized multi-instrument cross-calibration frameworks beyond astronomy
- Sectors: energy and climate (satellite remote sensing), healthcare (multi-modal imaging), robotics (multi-sensor fusion)
- Use case: adapt “interstitial reference” and physics-based color law ideas to cross-calibrate fleets of sensors (e.g., satellites, medical scanners) using shared spectral/physical standards and overlapping targets to reduce inter-instrument biases.
- Tools/products/workflows: reference target catalogs (spectral phantoms/standards), passband or modality response modeling, probability-weighted fusion to handle “contamination” (non-target signals).
- Assumptions/dependencies: availability of trusted standards; accurate instrument response characterization; domain-specific adaptation of color/SED laws; regulatory approval for clinical use cases.
- Standardized uncertainty accounting and evidence-based model preference in large collaborations
- Sectors: academia, finance, software engineering, policy
- Use case: institutionalize systematic covariance construction (as in Eq. for Csyst), nested sampling for evidence, and publishing of prior choices; use evidence ratios alongside frequentist significance in decision-making (e.g., scientific claims, model deployment).
- Tools/products/workflows: reproducible pipelines with systematic toggles; evidence calculators (Nautilus/Polychord/MultiNest); governance guidelines for priors and model comparison.
- Assumptions/dependencies: organizational buy-in; training in Bayesian methodology; compute resources; clear thresholds for “weak,” “moderate,” and “strong” preference.
- Cost-effective photometric-only cosmology at scale
- Sectors: academia, research infrastructure policy
- Use case: reduce reliance on spectroscopic confirmation by maturing photometric classification plus contamination-aware inference (BEAMS), enabling larger cosmological samples at lower cost.
- Tools/products/workflows: high-fidelity simulations for classifier training; continuous domain-adaptation; routine performance audits; probabilistic weighting in inference pipelines.
- Assumptions/dependencies: stable classifier generalization across redshift and survey conditions; validated low contamination rates; ongoing monitoring and recalibration.
- Bias-correction-aware ML for time-series analytics in other domains
- Sectors: finance (event classification), energy (grid anomalies), healthcare (wearable signals)
- Use case: translate BBC-like simulation-informed bias corrections and BEAMS-like mixture modeling to time-series classification systems where selection effects and contamination bias downstream inference.
- Tools/products/workflows: simulation frameworks to replicate detection/selection processes; probabilistic labels and contamination priors; joint estimation of nuisance parameters (analogous to α, β).
- Assumptions/dependencies: ability to model selection/detection pipelines; access to representative training data; organizational willingness to report and propagate uncertainty.
- Expanded white dwarf spectral standards and calibration products
- Sectors: academia, instrumentation vendors
- Use case: develop commercial-grade calibration packages (spectral libraries, ETL tools for passbands, uncertainty models) for observatories and instrument manufacturers.
- Tools/products/workflows: curated DA white dwarf catalogs; automated passband fitting and monitoring; APIs for calibration ingestion.
- Assumptions/dependencies: sustained observational programs; vendor collaboration; quality assurance standards; ongoing updates with Gaia/HST releases.
Glossary
- AAOmega spectrograph: A multi-object optical spectrograph used to obtain galaxy and supernova spectra. Example: "OzDES on the AAOmega spectrograph"
- Atacama Cosmology Telescope (ACT): A millimeter-wave telescope in Chile that measures the cosmic microwave background with high resolution. Example: "Atacama Cosmology Telescope (ACT)"
- Baryon acoustic oscillations (BAO): Regular, periodic fluctuations in the density of the visible baryonic matter of the universe that serve as a standard ruler for cosmology. Example: "Measurements of baryon acoustic oscillations (BAO)"
- Bayesian evidence: The marginal likelihood of the data under a model, used to compare models by integrating the likelihood over the prior. Example: "others preferring Bayesian evidence"
- BEAMS with Bias Correction (BBC): A method that combines Bayesian classification with simulation-based bias corrections to infer supernova distances and cosmology. Example: "The BEAMS with Bias Correction (BBC) method"
- candl likelihood: A software likelihood package for using SPT and other CMB data in cosmological inference. Example: "implemented in the candl likelihood"
- cosmic microwave background (CMB): Relic radiation from the early universe used to constrain cosmological parameters. Example: "cosmic microwave background (CMB)"
- DA white dwarfs: Hydrogen-atmosphere white dwarfs used as spectrophotometric standards for precise calibration. Example: "The addition of DA white dwarfs"
- Dark Energy Camera (DECam): A wide-field optical imager on the Blanco 4-m telescope used by DES. Example: "Dark Energy Camera (DECam"
- DESI DR2: The second data release from the Dark Energy Spectroscopic Instrument, providing BAO measurements among other datasets. Example: "DESI DR2"
- Differential Chromatic Refraction: Wavelength-dependent refraction by Earth’s atmosphere that shifts object positions and affects photometry. Example: "Differential Chromatic Refraction"
- Directional Light Radius (d_DLR): A metric to associate a supernova with its most likely host galaxy based on distance scaled by galaxy light profile. Example: "Directional Light Radius ()"
- Dust2Dust: A population model describing supernova and dust parameters used in simulations for bias corrections. Example: "Dust2Dust"
- equation-of-state parameter: The ratio w = P/ρ describing dark energy’s pressure-to-density relation; w = −1 for a cosmological constant. Example: "equation-of-state parameter"
- F99 Colour Law: The Fitzpatrick (1999) extinction law specifying wavelength-dependent dust reddening used in SN modeling. Example: "F99 Colour Law"
- Flat ΛCDM: The standard cosmological model with a cosmological constant (Λ), cold dark matter (CDM), and zero spatial curvature. Example: "Flat CDM"
- Flat CDM: A dark energy model allowing time-varying equation of state w(a) = w0 + (1−a)wa in a spatially flat universe. Example: "Flat CDM"
- Fragilistic: A cross-survey photometric calibration solution that preceded Dovekie in DES analyses. Example: "Fragilistic calibration solution"
- Gaia spectroscopy: Spectral data from the Gaia mission used to characterize filters and improve cross-calibration. Example: "Gaia spectroscopy"
- Hubble Diagram: A plot of distance modulus versus redshift used to infer the expansion history of the universe. Example: "Hubble Diagram"
- initial mass function: The distribution of stellar masses at formation used in host galaxy modeling. Example: "initial mass function"
- luminosity distance: A distance measure inferred from observed flux and intrinsic luminosity, entering SN distance moduli. Example: "The luminosity distance is given by"
- mass step: An empirical luminosity offset in standardized SN Ia magnitudes correlated with host-galaxy stellar mass. Example: "the `mass step'"
- Markov Chain Monte Carlo (MCMC): A sampling method for exploring parameter posteriors in high-dimensional spaces. Example: "MCMC"
- Nautilus: A nested sampling algorithm used to sample posteriors and compute Bayesian evidence. Example: "Nautilus"
- OzDES: A spectroscopic follow-up program for DES using the Anglo-Australian Telescope to obtain host galaxy redshifts. Example: "OzDES"
- Pantheon+: A compilation of low- and high-redshift SNe Ia used for cosmological analyses. Example: "Pantheon+"
- PEGASE2 templates: Galaxy spectral templates used to estimate host galaxy properties like stellar mass and color. Example: "PEGASE2 templates"
- peculiar velocities: Deviations from pure Hubble flow due to local gravitational motions, important at low redshift. Example: "peculiar velocities"
- principal component analysis: A statistical method; in SALT it motivates the decomposition of SN SED variability. Example: "similar to a principal component analysis"
- SALT2 model: An empirical spectral time-series model for Type Ia supernovae used to fit light curves. Example: "SALT2 model"
- SALT3 model: An updated SALT model with expanded training data and wavelength coverage for improved SN fitting. Example: "SALT3 model"
- scale factor: The cosmological expansion factor a = 1/(1+z) used in parameterizing w(a). Example: "scale factor"
- Scene Modelling Photometry (SMP): A photometry pipeline that simultaneously models SN and host-galaxy flux. Example: "Scene Modelling Photometry"
- spectral energy distribution (SED): The flux of an object as a function of wavelength or frequency; central to SN modeling. Example: "spectral energy distribution (SED)"
- SPT-3G: The third-generation camera on the South Pole Telescope providing high-precision CMB measurements. Example: "SPT-3G"
- SuperNNova (SNN): A recurrent neural network classifier trained on SN photometry to assign SN types. Example: "SuperNNova (SNN"
- transverse comoving distance: The comoving distance across the line of sight, entering cosmological distance calculations. Example: "The transverse comoving distance is"
- Tripp estimator: A linear relation using fitted SN parameters (mB, x1, c) to estimate distance modulus. Example: "Tripp estimator"
- TTTEEE: Combined temperature and E-mode polarization power spectra of the CMB used for parameter constraints. Example: "TTTEEE"
- Union3: A supernova compilation/analysis showing evidence for time-varying dark energy. Example: "Union3"
- Wilks' Theorem: A result giving the distribution of likelihood ratio statistics for nested models, used for model preference. Example: "Wilk's Theorem"
- ZP offsets: Photometric zero-point adjustments used to align calibration between surveys. Example: "ZP offsets"
Collections
Sign up for free to add this paper to one or more collections.