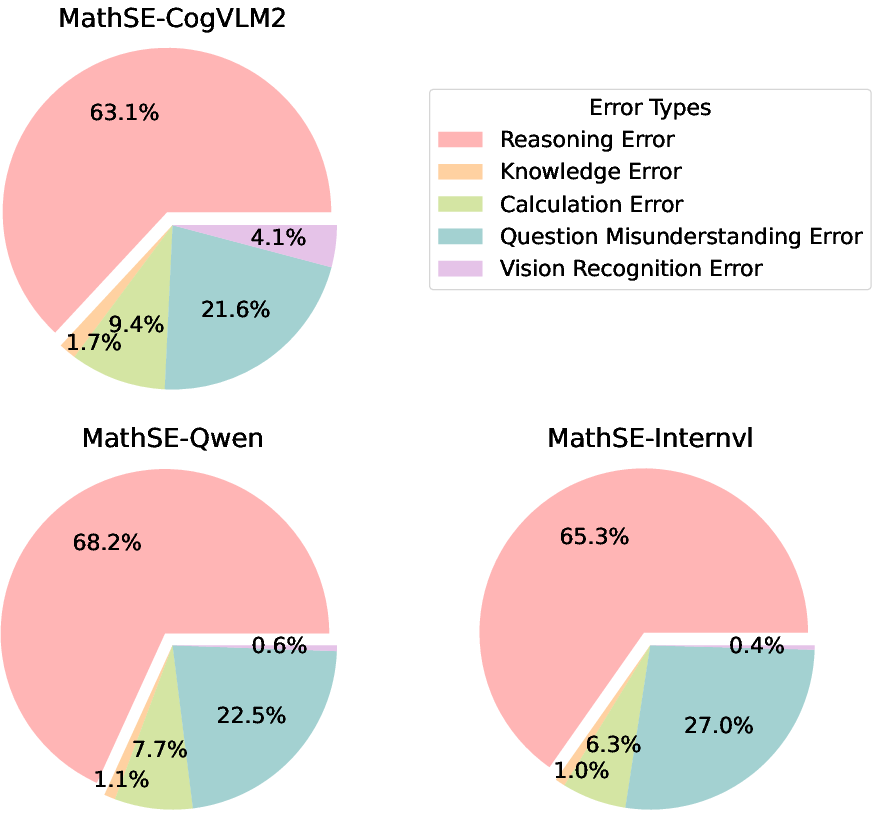MathSE: Improving Multimodal Mathematical Reasoning via Self-Evolving Iterative Reflection and Reward-Guided Fine-Tuning (2511.06805v1)

Abstract: Multimodal LLMs (MLLMs) have demonstrated remarkable capabilities in vision-language answering tasks. Despite their strengths, these models often encounter challenges in achieving complex reasoning tasks such as mathematical problem-solving. Previous works have focused on fine-tuning on specialized mathematical datasets. However, these datasets are typically distilled directly from teacher models, which capture only static reasoning patterns and leaving substantial gaps compared to student models. This reliance on fixed teacher-derived datasets not only restricts the model's ability to adapt to novel or more intricate questions that extend beyond the confines of the training data, but also lacks the iterative depth needed for robust generalization. To overcome these limitations, we propose \textbf{\method}, a \textbf{Math}ematical \textbf{S}elf-\textbf{E}volving framework for MLLMs. In contrast to traditional one-shot fine-tuning paradigms, \method iteratively refines the model through cycles of inference, reflection, and reward-based feedback. Specifically, we leverage iterative fine-tuning by incorporating correct reasoning paths derived from previous-stage inference and integrating reflections from a specialized Outcome Reward Model (ORM). To verify the effectiveness of \method, we evaluate it on a suite of challenging benchmarks, demonstrating significant performance gains over backbone models. Notably, our experimental results on MathVL-test surpass the leading open-source multimodal mathematical reasoning model QVQ. Our code and models are available at \texttt{https://zheny2751\allowbreak-dotcom.github.io/\allowbreak MathSE.github.io/}.

• The paper introduces a self-evolving fine-tuning paradigm that uses ORM-guided error diagnosis and iterative reflection to enhance multimodal mathematical reasoning.
• It employs a three-stage pipeline with initial supervised fine-tuning on GPT-4o distilled data, followed by error detection and iterative corrective reflections.
• Empirical results show 8–16% accuracy gains on major mathematics benchmarks, demonstrating improved error reduction and adaptability in MLLMs.

MathSE: Iterative Self-Evolution for Multimodal Mathematical Reasoning in MLLMs

Motivation and Limitations of Static Fine-Tuning

Recent advances in Multimodal LLMs (MLLMs) have demonstrated strong performance on vision-language tasks, but their capabilities lag behind on complex mathematical reasoning. Traditional approaches largely rely on supervised fine-tuning with datasets distilled from powerful teacher models such as GPT-4o. While these methods yield improvements, the reliance on static, teacher-derived datasets constrains the model’s adaptability and generalization. Models trained in this manner often lack the iterative refinement necessary to address novel or more challenging problems, and inherit static reasoning patterns disconnected from evolving data distributions.

Human learning, in contrast, proceeds through cycles of practice, feedback, and reflection—enabling adaptive mastery and robust generalization. Motivated by this paradigm (Figure 1), MathSE introduces a dynamic, self-evolving learning framework for MLLMs, filling the gap between one-shot fine-tuning and the continuous self-improvement observed in human learning.

Figure 1: Illustration of the human learning process that inspires our approach.

MathSE Framework: Iterative Refinement via Outcome Reward and Reflection

MathSE employs a three-stage pipeline (Figure 2): (1) initial supervised fine-tuning via GPT-4o-distilled Chain of Thought data, (2) Outcome Reward Model (ORM)-guided error detection and feedback, and (3) iterative reflection and reward-guided fine-tuning. This design directly addresses the shortcomings of static datasets by enabling the model to learn from its own outputs and refine reasoning processes iteratively.

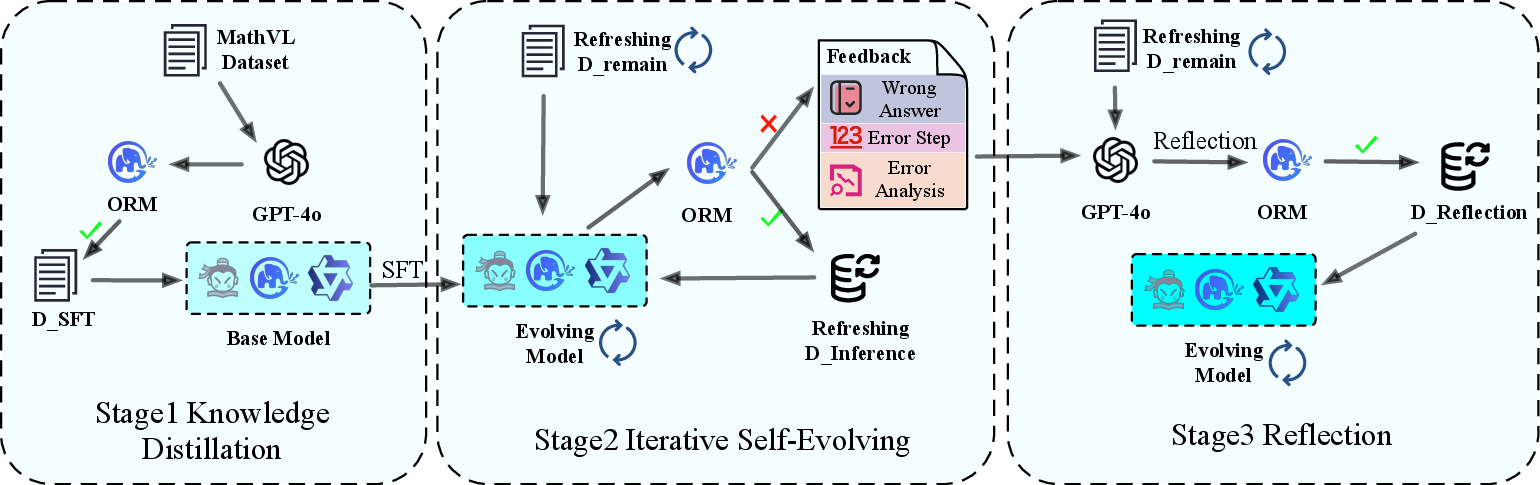
Figure 2: Overview of the MathSE Framework, which contains three stages to iteratively enhance mathematical reasoning abilities.

Initial Fine-Tuning

The process commences with standard supervised fine-tuning (SFT) on high-quality GPT-4o-distilled step-by-step reasoning traces. The objective is to bootstrap the model with foundational multimodal mathematical reasoning capability.

ORM-Guided Evaluation and Feedback

Post SFT, the model generates reasoning paths on the remaining corpus. A key innovation is the ORM—a dedicated verifier trained on a diverse corpus of correct and incorrect multimodal reasoning paths with step-localized error annotations (see Section 4.3). The ORM evaluates complete reasoning traces for global correctness, pinpoints the erroneous step if a mistake is detected, and produces detailed, actionable error analysis. This qualitative diagnostic feedback is crucial for deeper model introspection and targeted improvement, in contrast to scalar or binary rewards used in earlier outcome reward modeling paradigms.

Iterative Reflection and Fine-Tuning

Incorrect traces identified by the ORM, along with feedback, are provided as prompts to a powerful LLM (e.g., GPT-4o) to generate corrected, reflective reasoning paths via structured reflection prompts. These refined traces are incorporated back into the training set, and fine-tuning proceeds. The process repeats—each round leveraging improved reasoning and feedback to yield increasing gains in correctness and generalization.

Empirically, accuracy improves monotonically across self-evolving rounds (Figure 3), with the proportion of consistently correct samples rising significantly, and persistently incorrect samples decreasing.

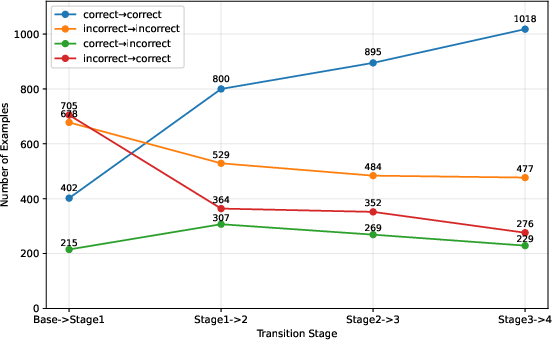
Figure 3: Accuracy changes during self-evolving process.

Implementation Details and Data Considerations

Three competitive MLLM backbones (CogVLM2, Qwen2-VL-7B, and InternVL2.5-8B) are used to instantiate MathSE, finely balancing between scale, architectural diversity, and visual-processing competence. The training pipeline employs large-scale, diverse multimodal math datasets (MathVL, GeoQA+, ChartQA, etc.), with careful data curation to maximize coverage across mathematical domains and complexity.

The ORM is realized through SFT on 60k annotated traces consisting of paired correct and incorrect solutions, with comprehensive error typologies (reasoning, knowledge, calculation, question understanding, vision recognition). Ablations indicate strong performance improvements when including detailed error-step identification and analysis, with overall ORM accuracy on binary judgment exceeding 97%.

Empirical Results

Benchmark Performance

Across standard math multimodal benchmarks (MathVista, MathVerse, MathVision, MathVL-test), MathSE produces substantial gains over both base models and state-of-the-art open-source models. On MathVL-test, MathSE-InternVL achieves 65.13% accuracy—a notable improvement (12+ points) over the leading open-source QVQ-72B and closed-source frontier models such as Claude 3.5 Sonnet and GPT-4o. All three MathSE variants exhibit large absolute improvements (8–16%) across mathematics benchmarks when compared to their respective backbones.

Ablation and Error Analysis

Ablations confirm that the self-evolving training regime using both initial distilled data and model-generated, ORM-filtered traces (240k total) leads to ~4% higher accuracy than a pure 240k GPT-4o baseline. The inclusion of ORM-guided reflection yields further improvements over using GPT-4o reflections or omitting reflection altogether.

The error analysis (Figure 4) indicates that reasoning errors dominate residual mistakes, followed by question misunderstanding, knowledge errors, and minor contributions from calculation or visual recognition errors. Exemplars of correct, refined, and erroneous reasoning paths and ORM feedback are provided (Figures 5–11), illustrating the framework’s diagnostic interpretability.

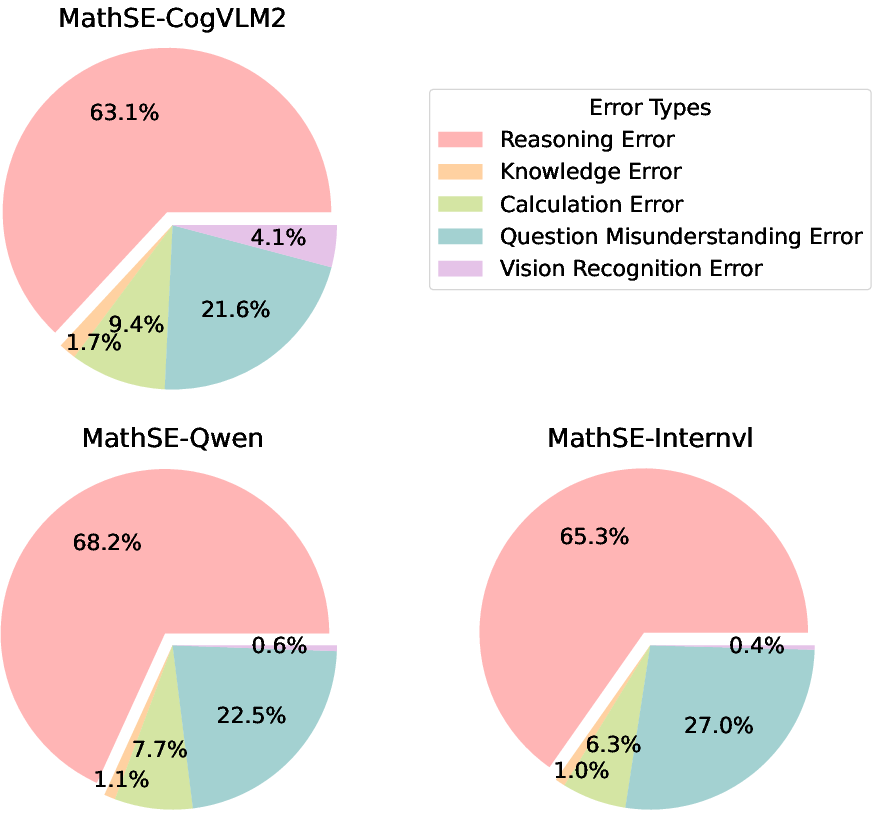
Figure 4: Distribution of different error types across three models on MathVL-test.

Figure 5: Example of correct reasoning path generated by Math-Vision.

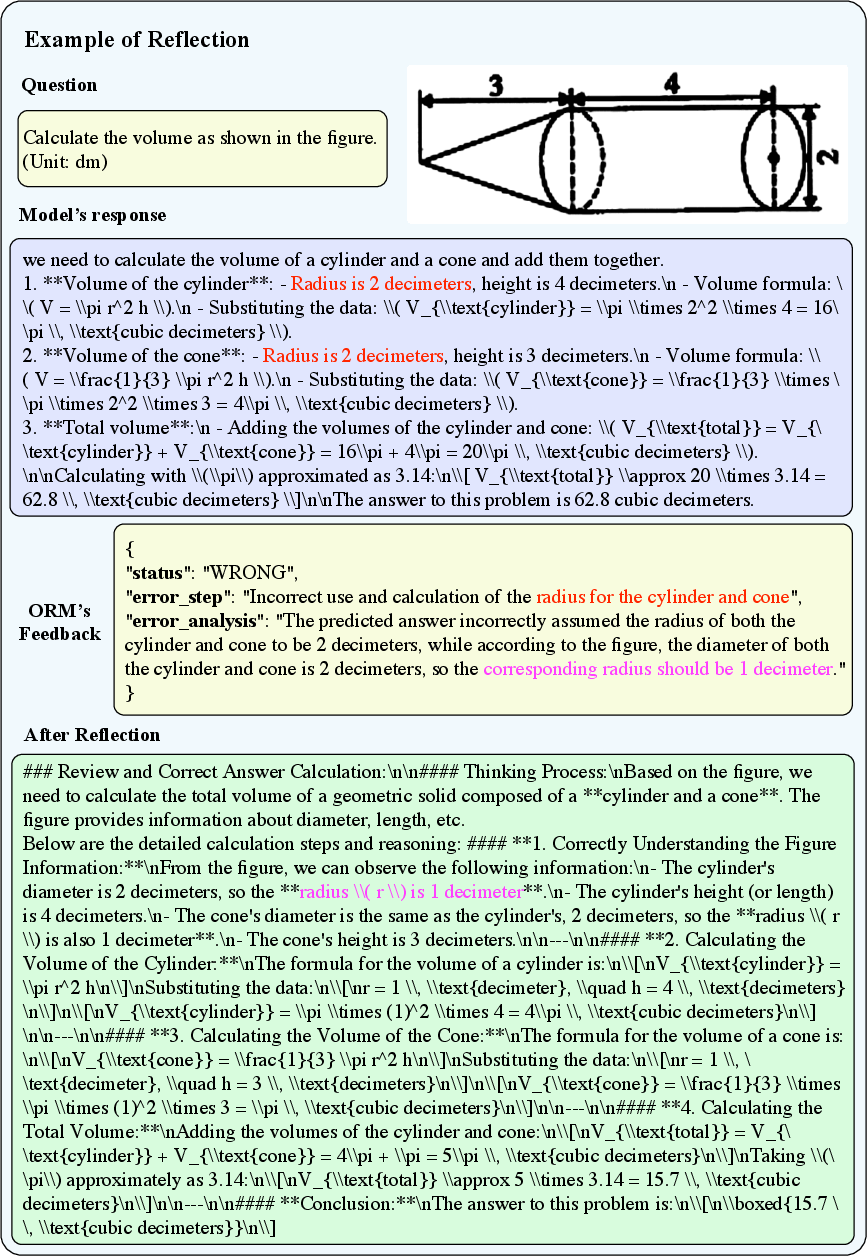
Figure 6: Example of reflection generated with incorrect reasoning path and ORM's Feedback.

Figure 7: Example of reasoning error identified by our ORM.

Figure 8: Example of knowledge error identified by our ORM.

Figure 9: Example of calculation error identified by our ORM.

Figure 10: Example of question understanding error identified by our ORM.

Figure 11: Example of vision recognition error identified by our ORM.

Theoretical and Practical Implications

The iterative, diagnostic reflection approach in MathSE offers theoretically stronger alignment with human learning, facilitating robust adaptation to out-of-distribution mathematical problems. In contrast to approaches that aggressively distill teacher output or rely on reward modeling that only computes scalar or binary scores, MathSE leverages step-localized, interpretable feedback, supporting trace-level introspection and fine-grained correction.

Practically, MathSE closes the gap between static supervision and true self-improvement, providing a scalable path for multi-modal mathematical skill acquisition without heavy reliance on ever-larger labeled datasets or inflexible teacher models. The paradigm is modular, generalizing to related domains where complex reasoning over language and vision is required.

Future Directions

Despite substantial improvements, the error breakdown suggests opportunities for enhancing language-vision alignment and improving capacities for abstract multi-hop reasoning. ORM development could benefit from explicit causal tracing, and external symbolic verifiers could be integrated for tasks requiring formal correctness. Combining MathSE with process-supervision techniques that track intermediate state spaces may enhance both transparency and robustness.

The self-evolving, reflection-centric training paradigm introduced in MathSE is applicable beyond mathematical reasoning; other domains with scarce labeled data and strong multi-step reasoning demands may benefit from similar iterative refinement approaches.

Conclusion

MathSE establishes an iterative, self-evolving fine-tuning paradigm for MLLMs, uniting outcome-guided error diagnosis and high-quality reflection to yield significant gains on complex multimodal mathematical reasoning. This work substantiates the value of human-inspired, iterative training methodologies, setting a foundation for future models capable of robust adaptive reasoning and efficient self-correction.