- The paper presents a novel self-evolution framework that uses Monte Carlo Tree Search and code-augmented chain-of-thought to improve math reasoning in small LLMs.
- It introduces a Process Preference Model that refines reasoning steps through pairwise ranking, leading to higher solution accuracy on benchmarks.
- Experimental results show significant performance boosts, with improvements up to 90% on the MATH benchmark and superior results on Olympiad-level tests.
rStar-Math: Small LLMs Excel in Math Reasoning Through Self-Evolved Deep Thinking
The paper "rStar-Math: Small LLMs Can Master Math Reasoning with Self-Evolved Deep Thinking" (2501.04519) introduces rStar-Math, a novel approach that enables small LLMs (SLMs) to achieve state-of-the-art performance in mathematical reasoning. This is accomplished through a self-evolutionary process leveraging Monte Carlo Tree Search (MCTS) for "deep thinking," guided by an SLM-based process reward model (PRM). The key innovations include code-augmented CoT data synthesis, a process preference model (PPM) training method, and a self-evolution recipe for iteratively improving reasoning capabilities.
Key Methodological Innovations
The rStar-Math framework hinges on three primary innovations designed to overcome the challenges of training SLMs for complex mathematical reasoning.
Code-Augmented CoT Data Synthesis
This method addresses the issue of unreliable intermediate steps in generated reasoning trajectories. It leverages MCTS to decompose problem-solving into multi-step generation. At each step, the policy SLM samples candidate nodes, generating both a one-step CoT and corresponding Python code (Figure 1). Only nodes with successful code execution are retained, ensuring the correctness of intermediate steps. Furthermore, extensive MCTS rollouts assign a Q-value to each step based on its contribution to trajectories leading to the correct answer, thereby identifying high-quality reasoning steps.

Figure 1: An illustration of how the policy model generates a one-step NL CoT alongside its corresponding Python code.
Process Preference Model (PPM) Training
Training a reliable PRM for math reasoning has been an open question. Instead of directly using noisy Q-values as reward labels, the PPM leverages Q-values to distinguish between positive (correct) and negative (incorrect) steps. This method constructs preference pairs for each step based on Q-values and uses a pairwise ranking loss to optimize PPM's score prediction for each reasoning step, achieving more reliable labeling.
Self-Evolution Recipe
rStar-Math employs a four-round self-evolution recipe to progressively build both a frontier policy model and PPM from scratch (Figure 2). In each round, the latest policy model and PPM are used to perform MCTS, generating increasingly high-quality training data. This iterative process refines the policy SLM, improves the PPM's reliability, generates better reasoning trajectories via PPM-augmented MCTS, and expands training data coverage to tackle more challenging problems.
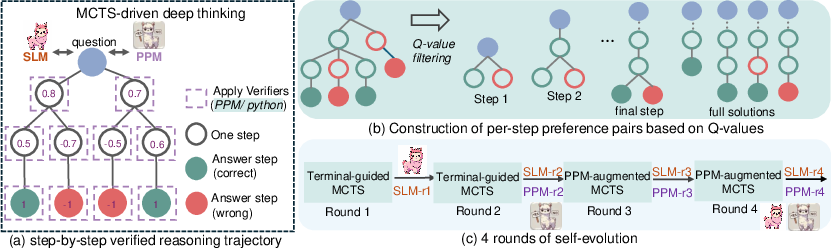
Figure 2: A visual representation of the rStar-Math framework showing a system diagram.
Experimental Results and Analysis
Extensive experiments across four SLMs (1.5B-7B) and seven math reasoning tasks demonstrate the effectiveness of rStar-Math. Notably, rStar-Math improves all four SLMs, matching or even surpassing OpenAI o1 on challenging math benchmarks. On the MATH benchmark, rStar-Math boosts Qwen2.5-Math-7B from 58.8\% to 90.0\% and Phi3-mini-3.8B from 41.4\% to 86.4\%, outperforming o1-preview by +4.5\% and +0.9\%. On the Olympiad-level AIME 2024, rStar-Math solves an average of 53.3\% (8/15) of the problems, exceeding o1-preview by 8.7\% and all other open-sourced LLMs (Table 1).
Ablation Studies
Ablation studies validate the superiority of step-by-step verified reasoning trajectories over state-of-the-art data synthesis baselines, as well as the PPM's effectiveness compared to outcome reward models and Q-value-based PRMs. These studies confirm that the three proposed innovations contribute significantly to the overall performance of rStar-Math.
Intrinsic Self-Reflection
One unexpected finding is the emergence of intrinsic self-reflection capability within the MCTS-driven deep thinking process (Figure 3). The model can recognize errors and self-correct with a correct answer, even without explicit self-reflection training data or prompts. This suggests that advanced System 2 reasoning can foster intrinsic self-reflection.
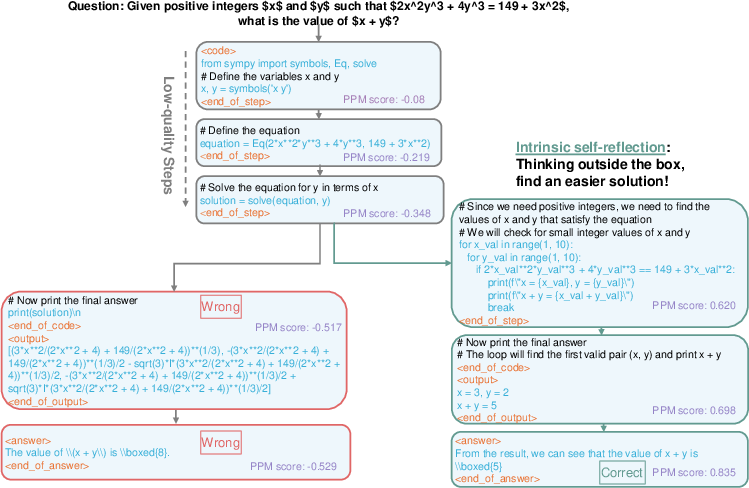
Figure 3: An example illustrating rStar-Math's ability to recognize low-quality reasoning steps and backtrack to simpler approaches.
Scaling Test-Time Compute
Increasing test-time computation improves reasoning accuracy across all benchmarks, though with varying trends (Figure 4). On Math, AIME, and Olympiad Bench, rStar-Math shows saturation or slow improvement at 64 trajectories, while on College Math, performance continues to improve steadily.

Figure 4: Showing the trends in reasoning performance when scaling up the test-time compute.
PPM's Influence
Experiments indicate that the PPM is the key determinant of the upper performance limit in System 2 deep thinking. The PPM shapes the reasoning boundary in System 2 deep thinking (Figure 5), effectively identifying critical theorem-application intermediate steps within the policy model's deep thinking process. These steps are predicted with high reward scores, guiding the policy model to generate the correct solution.
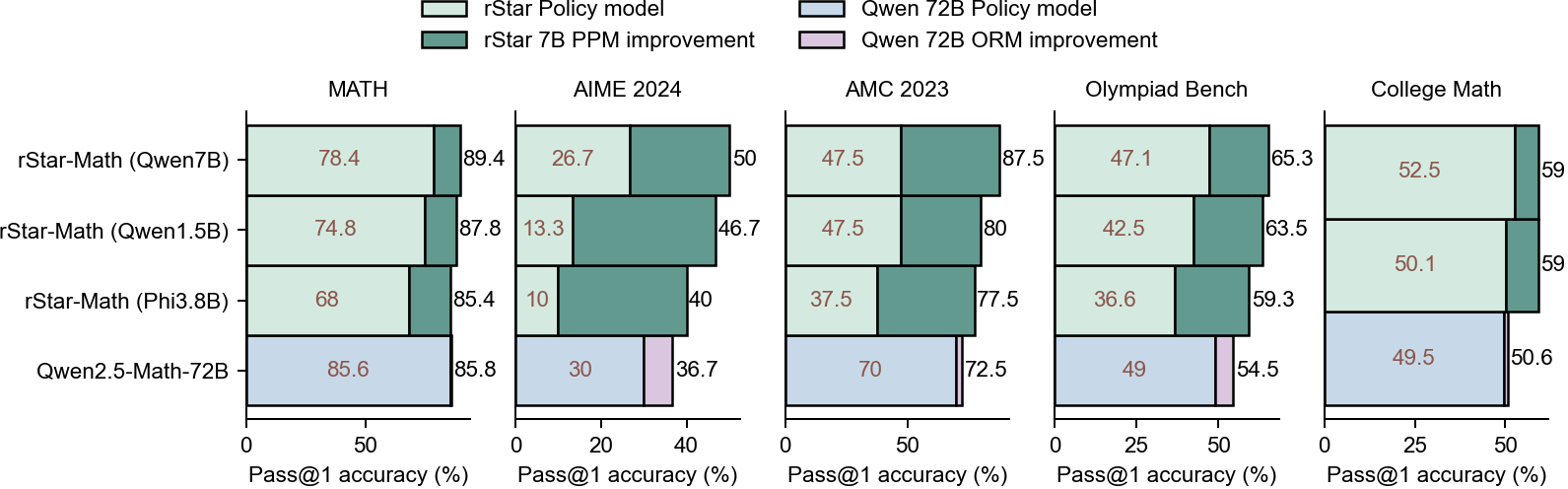
Figure 5: A visual showing that reward models primarily determine the final performance.
Implications and Future Directions
The rStar-Math framework presents a compelling approach for enhancing the mathematical reasoning capabilities of SLMs, achieving performance comparable to or even surpassing larger models like OpenAI's o1. The innovations in data synthesis, reward modeling, and self-evolution offer valuable insights for training SLMs in other complex reasoning tasks. Future research could explore generalizing rStar-Math to other domains, such as code and commonsense reasoning, and further improving its ability to solve challenging math problems by incorporating external knowledge and tools.
Conclusion
rStar-Math demonstrates that small LLMs can achieve state-of-the-art performance in mathematical reasoning through a self-evolved deep thinking approach. The paper's key contributions include a novel code-augmented CoT data synthesis method, a process preference model training approach, and a self-evolution recipe for iteratively improving reasoning capabilities. The experimental results and analysis highlight the effectiveness of rStar-Math and provide valuable insights for training SLMs in complex reasoning tasks.




