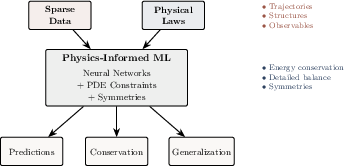
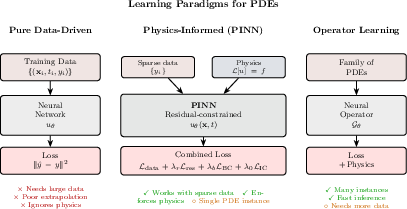
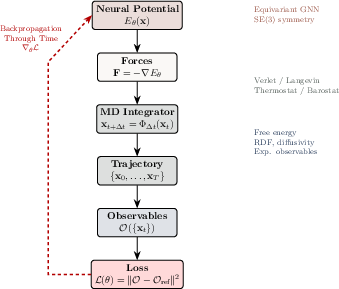
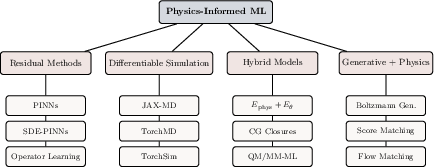
Learning Biomolecular Motion: The Physics-Informed Machine Learning Paradigm (2511.06585v1)

Abstract: The convergence of statistical learning and molecular physics is transforming our approach to modeling biomolecular systems. Physics-informed machine learning (PIML) offers a systematic framework that integrates data-driven inference with physical constraints, resulting in models that are accurate, mechanistic, generalizable, and able to extrapolate beyond observed domains. This review surveys recent advances in physics-informed neural networks and operator learning, differentiable molecular simulation, and hybrid physics-ML potentials, with emphasis on long-timescale kinetics, rare events, and free-energy estimation. We frame these approaches as solutions to the "biomolecular closure problem", recovering unresolved interactions beyond classical force fields while preserving thermodynamic consistency and mechanistic interpretability. We examine theoretical foundations, tools and frameworks, computational trade-offs, and unresolved issues, including model expressiveness and stability. We outline prospective research avenues at the intersection of machine learning, statistical physics, and computational chemistry, contending that future advancements will depend on mechanistic inductive biases, and integrated differentiable physical learning frameworks for biomolecular simulation and discovery.

• The paper introduces physics-informed machine learning to integrate physical laws with data-driven models for enhanced biomolecular motion prediction.
• It details frameworks like PINNs, operator learning, and differentiable MD to enforce energy conservation and thermodynamic constraints.
• The study discusses limitations and future directions for scaling these methods in modeling protein folding, kinetics, and catalysis.

Physics-Informed Machine Learning for Biomolecular Motion: Paradigms, Frameworks, and Implications

The reviewed paper provides a comprehensive account of the interface between molecular simulation and machine learning, specifically focusing on the physics-informed machine learning (PIML) paradigm in biomolecular dynamics. The discussion spans theoretical underpinnings, methodological innovations, the emerging software ecosystem, practical limitations, and future perspectives. The central thesis is that effective integration of domain-specific physical priors with data-driven methods yields models that are simultaneously predictive, stable, interpretable, and generalizable, enabling modeling of biomolecular phenomena such as protein folding, free-energy estimation, and enzyme catalysis beyond the capabilities of either approach in isolation.

Figure 1: The physics-informed machine learning paradigm integrating sparse data and governing physical laws in neural models to enhance accuracy, stability, and generalization.

The Physical Basis of PIML in Molecular Systems

The foundation of molecular modeling is rooted in statistical mechanics and thermodynamics, where the probability distribution of molecular conformations is governed by the Boltzmann distribution with the free energy landscape encapsulating both stability and accessibility of states. Classical molecular dynamics (MD) using empirical force fields has been limited by sampling inefficiencies and the inability to capture rare events or long-timescale conformational changes due to timescale separation and the curse of dimensionality.

PIML addresses these constraints by embedding physical structure into learning algorithms. Constraints take the form of energy conservation, detailed balance, symmetries (E(3)/SE(3)), and variational principles, enforcing that learned models respect thermodynamic and kinetic laws. The convergence of energy-based models and learning dynamics, such as Hopfield networks and Boltzmann machines, exemplifies the longstanding connection between physical systems and trainable neural models.

Paradigms for Learning PDE-Governed Molecular Dynamics

A central motif is the enforcement of physical laws through loss functions and inductive biases. The core frameworks analyzed include:

• Physics-Informed Neural Networks (PINNs): These networks minimize composite losses incorporating data fidelity, PDE residuals, boundary, and initial-condition constraints. By leveraging automatic differentiation, PINNs enforce physical admissibility throughout space-time, stabilizing learning where data is sparse.
• Operator Learning Architectures: Models such as DeepONet and the Fourier Neural Operator generalize to families of PDEs, enabling rapid surrogate predictions for varying conditions and system parameters.
• Differentiable Simulation: End-to-end differentiable MD engines (e.g., JAX-MD, TorchMD, TorchSim) allow gradients to flow through integrators, thermostats, and potentials, supporting the direct optimization of physical parameters and force fields against observable-level objectives.

  Figure 2: Contrasting pure data-driven, PINN-based, and operator-learning paradigms for PDE-constrained modeling in biomolecular systems.

Hybrid Physics-ML Potentials and Differentiable MD Engines

The paper establishes that hybridization is essential to bridge the gap between trusted physical models and data-driven corrections. ML potentials account for neglected many-body, electronic, and environmental interactions while maintaining the variational structure required by physical consistency. The hybrid paradigm is formalized as:

$$E_{\mathrm{hyb}}(\mathbf{x}) = E_{\mathrm{phys}}(\mathbf{x}) + E_\theta(\mathbf{x})$$

This structure ensures conservative dynamics, compliance with the fluctuation-dissipation theorem (FDT), and thermodynamic consistency at both equilibrium and nonequilibrium. Differentiable simulation is emphasized for trajectory-centric learning (e.g., learning from observables such as free energies, mean first-passage times, or experimental measurements), providing a flexible and scalable approach for optimizing over both microscopic and ensemble properties.

Figure 3: An ideal differentiable simulation pipeline where the learned potential influences an MD integrator, with observables used for backpropagation to refine model parameters.

Figure 4: Taxonomy of PIML frameworks, spanning residual-based PINNs, operator learning, differentiable MD, hybrid closures, and physics-aware generative models.

Applications in Biomolecular Science

Free-Energy Surface (FES) Learning: PIML frameworks jointly optimize collective variables (CVs) and the associated free-energy profiles, guided by variational and thermodynamic priors. Spectral operator methods (e.g., VAMPnets) and normalizing-flow/Boltzmann generator models enable unbiased equilibrium sampling and estimation of $F(s)$. Surrogate models with automatic differentiation further allow for direct mapping between atomic configurations and CVs without analytic Jacobians.

Protein Folding and Kinetics: Equivariant GNN-based potentials and hybrid PINN frameworks have demonstrated strong results in capturing both the static landscape and dynamic processes, e.g., fold switching and allosteric transitions. Operator-learning approaches recover slow modes and metastable state partitions, extrapolating kinetics from limited trajectory data.

Ligand Binding and Catalysis: Diffusion- and flow-based generative models conditioned by physical constraints facilitate binding pose generation and reweightable ensemble predictions. ML-augmented QM/MM approaches, as implemented in NequIP/GemNet-class GNNs, improve accuracy in catalysis and enzyme mechanism modeling by integrating learned short-range corrections with baseline QM or empirical force fields.

Practical Limitations and Failure Modes

The paper directly addresses several critical challenges:

• Extrapolation Limits: Neural networks are prone to unphysical predictions outside the domain of training data, particularly for strained geometries, rare events, or altered thermodynamic conditions. Architectural regularization and fallback to physical baselines are recommended for mitigation.
• Curse of Dimensionality: Scaling PINNs and neural operators to systems with thousands of degrees of freedom remains largely unsolved; current techniques rely on aggressive CV reduction, hierarchical representations, and operator sparsity.
• Numerical Stiffness: PINNs face difficulties with high-frequency dynamics, often requiring careful loss rebalance, symplectic integration, curriculum learning, or multiple shooting to stabilize training and improve accuracy on multi-timescale systems.
• Nonequilibrium Generalization: Models trained on equilibrium data may violate fluctuation theorems or predict negative entropy production in driven regimes. Pathwise loss terms and training on nonequilibrium trajectories become necessary for physically admissible predictions.
• Data Quality and Bias: The fidelity of PIML is fundamentally limited by the accuracy and coverage of training data. Benchmarks must account for systematic biases in force fields, QM methods, and experimental errors, with active learning, cross-validation, and uncertainty quantification used to target gaps and reduce overconfidence in sparse regimes.

Implications and Future Developments

The review underscores that PIML is not universally superior to classical or purely data-driven approaches. Its primary utility lies in contexts where partial physical knowledge coexists with expensive or limited data, and where consistent modeling across many related systems is required. In routine, low-dimensional or data-poor scenarios, standard numerical or simulation techniques remain preferable.

Future work will concentrate on integrating mechanistic inductive biases directly within architectures ("hard" constraints vs. "soft" penalties), scaling differentiable MD to GPU-native, multi-system simulations, and developing uncertainty-aware, physics-guided active learning for improved data efficiency. Pretraining on large molecular datasets with symmetry- and physics-aware objectives is expected to yield foundational models adaptable to new chemistries and environments with minimal fine-tuning.

Conclusion

By tightly coupling physical principles with machine learning, the PIML paradigm provides a pathway toward accurate, stable, and interpretable models of biomolecular systems. The reviewed frameworks—PINNs, operator networks, differentiable simulations, and hybrid closures—enable the direct incorporation of conservation laws, symmetries, and thermodynamic identities into modern learning techniques. While technical and computational challenges persist, particularly in scalability, model expressiveness, and uncertainty control, PIML methods are rapidly maturing, forming a robust foundation for future biomolecular modeling. The shift from isolated simulation or learning to hybrid, differentiable, and uncertainty-aware scientific modeling signals a paradigm where physics and data are no longer antagonistic but synergistic components of molecular science.