Deep Progressive Training: scaling up depth capacity of zero/one-layer models (2511.04981v1)

Abstract: Model depth is a double-edged sword in deep learning: deeper models achieve higher accuracy but require higher computational cost. To efficiently train models at scale, an effective strategy is the progressive training, which scales up model capacity during training, hence significantly reducing computation with little to none performance degradation. In this work, we study the depth expansion of large models through the lens of optimization theory and feature learning, offering insights on the initialization of new layers, hyperparameter transfer, learning rate schedule, and timing of model expansion. Specifically, we propose zero/one-layer progressive training for the optimal tradeoff between computation and loss. For example, zero/one-layer progressive training on GPT2 can save $\approx 80\%$ compute, or equivalently accelerate $\approx 5\times$ while achieving almost the same loss, compared to to a fully trained 60-layer model with 7B parameters.

• The paper presents zero/one-layer progressive training, enabling full-depth expansion from minimal layers with up to 80% compute savings and negligible loss degradation.
• It systematically evaluates initialization strategies and the WSD learning rate schedule, demonstrating that random initialization or layer copying ensures rapid convergence.
• Empirical tests on GPT2, ResNet, and MoE models confirm that single-stage expansion outperforms multi-stage approaches, yielding a 5× speedup with minimal validation loss delta.

Deep Progressive Training: Scaling Up Depth Capacity of Zero/One-Layer Models

Introduction and Problem Statement

The computational demand for training deep neural networks has dramatically increased with contemporary LLMs, motivating both empirical and theoretical work on compute-efficient training procedures. This paper addresses a central tradeoff: achieving the performance of deep models while drastically reducing training computational resources. Progressive training, or model growth—starting from a smaller model and expanding depth during training—has been considered previously but was generally limited to shallow expansions (e.g., $2\times$–$4\times$ depth increases, saving $30\%$–$50\%$ compute) and often with suboptimal optimization behaviors post-expansion. This work introduces and systematically analyzes zero/one-layer progressive training, where training begins from a network with zero or one trainable layer and expands directly to the full target depth, yielding up to $80\%$ computational savings (up to $5\times$ speedup) with negligible loss degradation (\textless$0.2\%$ validation loss delta on 7B parameter GPT2).

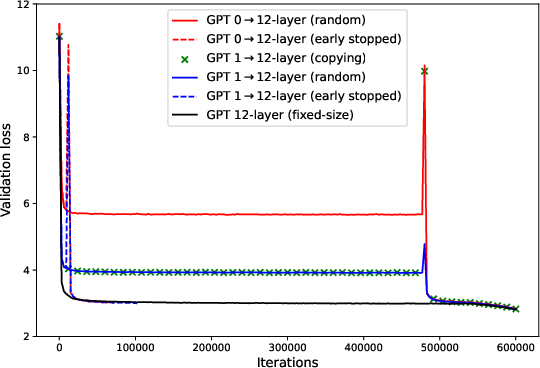
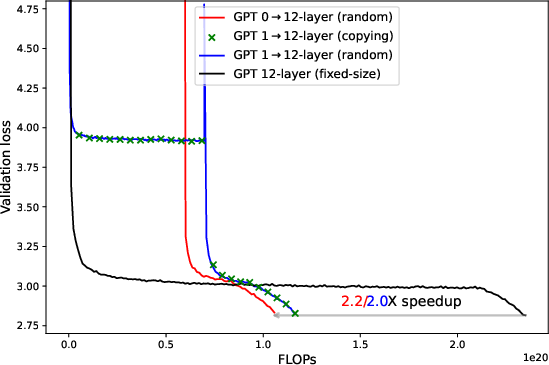
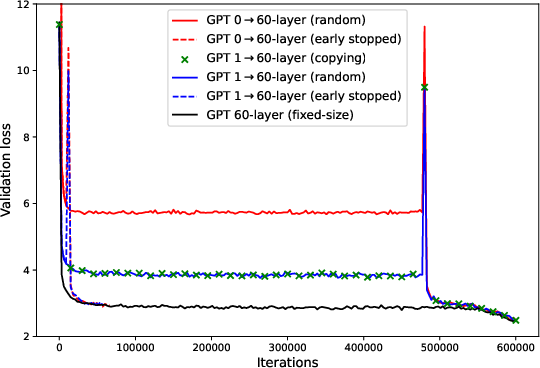
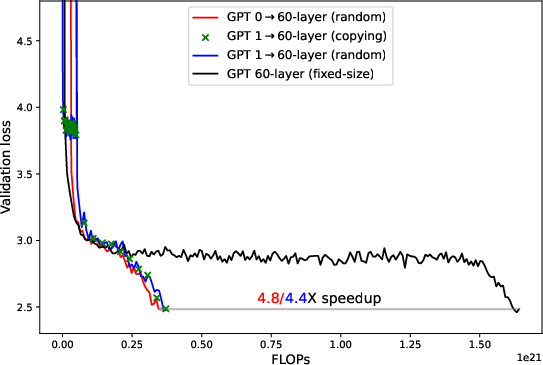
Figure 1: Zero-layer (red, 39M or 0.15B) and one-layer (blue and green, 46M or 0.27B) progressive training can achieve significant speedup over fixed-sized training (black, 12-layer 124M or 60-layer 7B) on GPT2 pre-trained on OpenWebText under WSD schedule. The difference in final validation loss is $<0.5\%$ for 124M runs and $<0.2\%$ for 7B runs.

Methodological Advances and Theoretical Foundations

Initialization Schemes for Depth Expansion

The paper rigorously benchmarks several approaches for initializing new layers at expansion:

• Random initialization and copying (cloning from pre-expansion layers) both provide empirically fast convergence and tractable optimization.
• Zero initialization is function-preserving but yields vanishing gradients and poor trainability.
• Hybrid copying-zero methods (setting specific sub-layers to zero) achieve function-preservation with partial trainability improvements, but remain suboptimal compared to pure copying or random initialization.

For zero-layer expansion, only random initialization is feasible; for one-layer, both random and copying are effective. The analysis connects these strategies to muP theory and feature-learning conditions, ensuring that feature norms remain stable post-expansion and hyperparameters (notably learning rates) can be transferred without retuning.

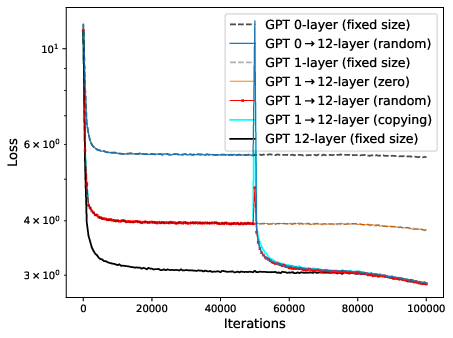
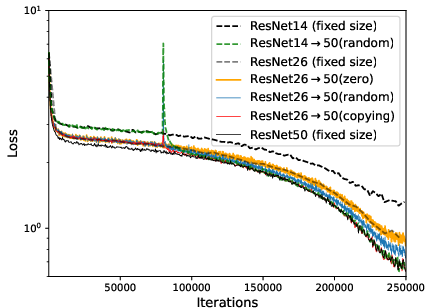
Figure 2: Convergence of zero/one-layer progressive training and fixed-size training. Left: ResNet with depth expansion at 32-th epoch. Right: GPT2 with depth expansion at 50k iterations.

Learning Rate Schedules and the WSD Regime

A strong empirical and theoretical finding is the critical role of learning rate (LR) scheduling. The Warmup-Stable-Decay (WSD) schedule, with a prolonged constant LR phase, enables the latest feasible expansion timing and minimizes validation loss. In contrast, cosine decay schedules are highly sensitive to the time of expansion and degrade more when expansion is delayed.

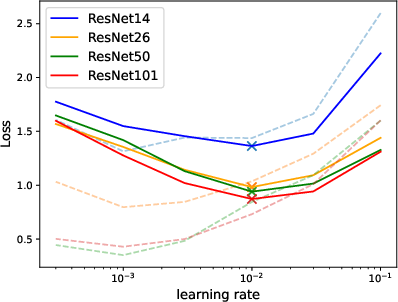
Figure 3: Validation (solid) and training loss (dashed) at different learning rates of Muon-NSGD.

Correspondingly, using the optimal Muon-NSGD optimizer with muP-scaling ensures that hyperparameters tuned for shallow models transfer robustly to the full, expanded depth.

Theoretical Analysis of Progressive Training Dynamics

The paper offers a convex optimization-based convergence theory for progressive training. The depth-expanded training can be framed as projected gradient descent (PGD) on the large model (with new parameters zeroed), followed by stochastic gradient descent (SGD) with optimally-initialized new layers. The final optimization gap versus scratch training is controlled by the proportion of training before expansion, the quality of the new layer initialization, and critically, the LR schedule. The theory explains why WSD schedules allow robust expansion late into training, while traditional decaying LR schedules fail.

Empirical Results: Scaling, Timing, and Tradeoffs

The authors perform extensive empirical studies on GPT2 (up to 7B, 60 layers), ResNet, and Mixture-of-Experts (MoE) models. Key outcomes include:

• Zero/one-layer progressive training allows expansion at up to $0.8T$ (80\% of iteration budget), yielding $5\times$ compute speedup for large models with negligible loss degradation.
• The mixing time (iterations needed for the expanded model to "catch up" to fixed-depth training) is mostly data-dependent ($\sim$number of tokens or images processed), not iteration-count dependent, and is robust to batch size.
• The method is effective across architectures: dense, residual, and MoE models.
• Multi-stage expansions (e.g., doubling depth several times) are not more efficient in loss-compute tradeoff and do not yield improved final accuracy, due to the discovered "mixing behavior" that post-expansion optimization rapidly amortizes the differences—single-stage expansion is preferable.

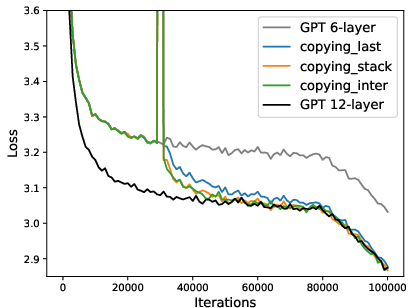
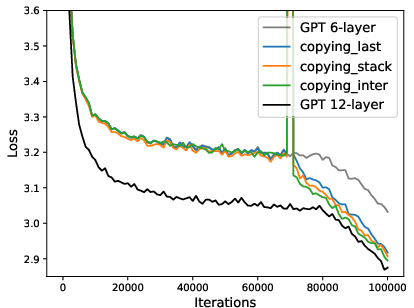
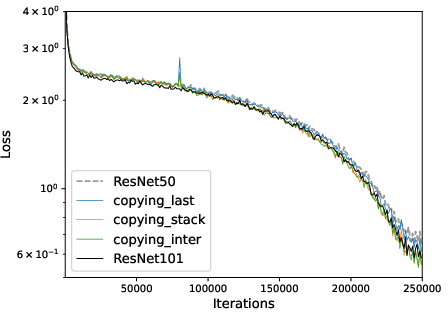
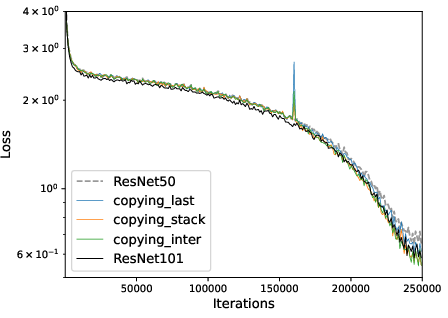
Figure 4: Convergence of multi-layer progressive training and fixed-size training. Left: ResNet with depth expansion at 32/64-th epoch. Right: GPT2 with depth expansion at 30/70k iterations.

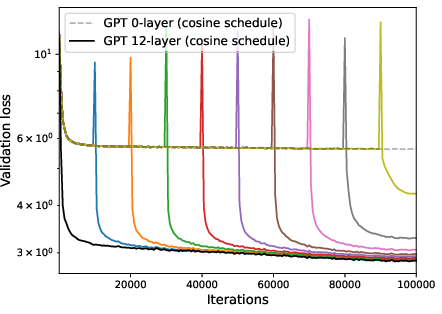
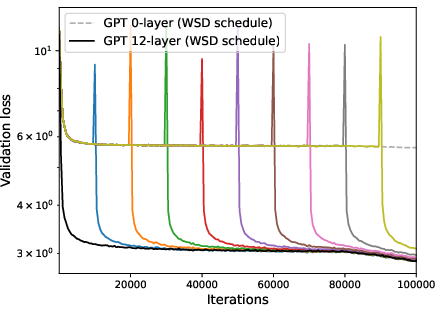
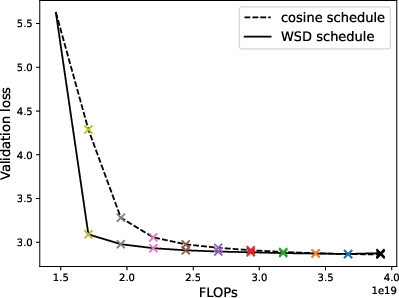
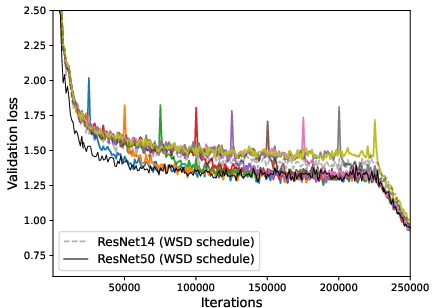
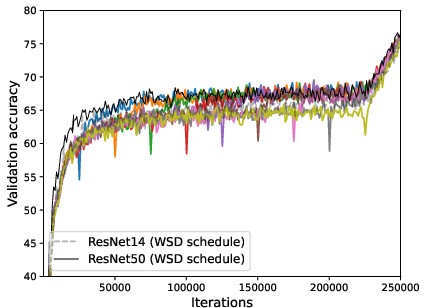
Figure 5: Performance of zero-layer progressive training and fixed-size training, where WSD schedule significantly enhances the progressive training.

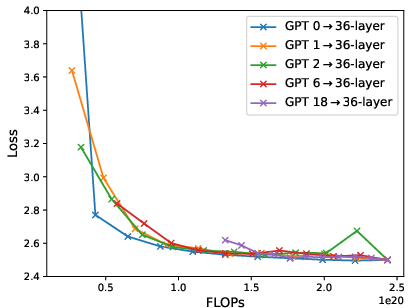
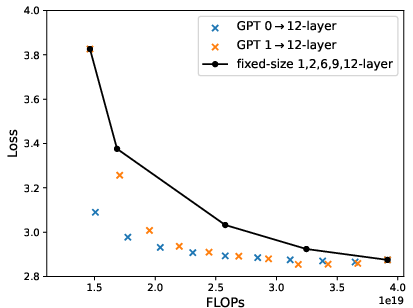
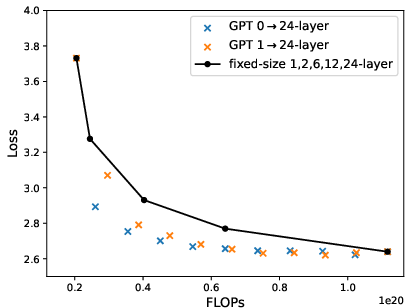
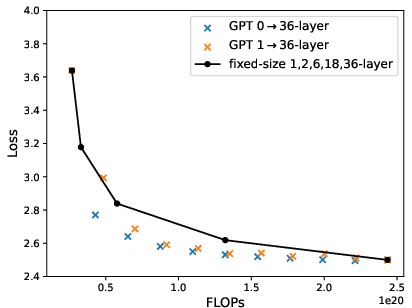
Figure 6: Loss-compute tradeoff (validation loss v.s. FLOPs) of depth expansion from small models to $\{12,24,36\}$-layer GPT2; zero/one-layer expansion achieves the near-optimal frontier.

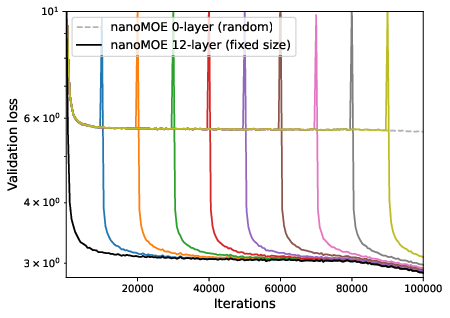
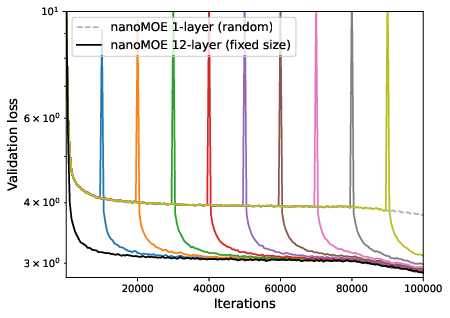
Figure 7: Convergence of zero/one-layer progressive training and fixed-size training for MoE, with random initialization of new layers.

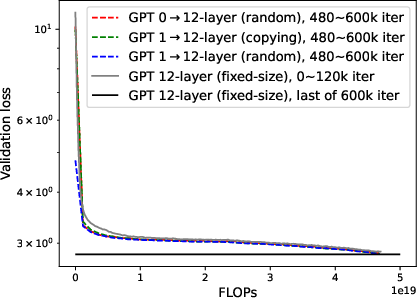
Figure 8: Under the same compute budget, progressive training converges much faster than fixed-size training, despite a transient increase in loss post-expansion.

Implementation Recommendations

The cumulative theoretical and empirical analysis yields a concrete recipe for efficient deep progressive training:

1. Start from zero- or one-layer model; expand to target depth using random initialization (or, for one-layer, copying).
2. Employ muP-scaled optimizers (e.g., Muon-NSGD) for robust hyperparameter transfer.
3. Adopt the WSD learning rate schedule with expansion scheduled in the stable LR phase; avoid expansion during or after LR decay.
4. Determine expansion timing via small-scale fixed-depth and progressive pilot runs, measuring when losses “mix.” Mixing times are data-dependent and can be reused for schedules within the same model family.
5. Single-stage expansion is empirically sufficient; multi-stage expansions do not outperform in efficiency or accuracy.

Practical and Theoretical Implications

This work rigorously demonstrates that training large, deep networks need not be synonymous with prohibitive computational resource consumption. The finding that full-depth models can emerge from single-layer precursors with minimal loss penalty has implications for resource-constrained settings and large-scale foundation model pretraining pipelines. For organizations retraining language or vision models over ever-growing data, zero/one-layer progressive training provides concrete, scalable methodology for $5\times$ compute efficiency gains without architectural compromises.

Theoretically, the result reinforces the utility of convex and muP-based analysis in predicting deep learning optimization behavior, especially in regimes with architectural changes mid-training. Further, the observation that expansion ordering and intermediate multi-stage growth are essentially unnecessary, once mixing behavior is properly recognized, will inform future model scaling approaches.

Conclusion

Zero/one-layer progressive training, when combined with careful initialization, muP-inspired optimization, and the WSD learning rate schedule, allows for near lossless and highly efficient scaling of deep network depth. Empirical results validate that this method achieves optimal compute/loss tradeoff and is robust across model families and scales. These findings suggest a viable paradigm for scaling both the depth and breadth of deep learning models under realistic compute constraints. Future research may extend these results to simultaneous width/depth expansions and finer control over sparse and modular architectures.