Towards Robust Mathematical Reasoning (2511.01846v1)
Abstract: Finding the right north-star metrics is highly critical for advancing the mathematical reasoning capabilities of foundation models, especially given that existing evaluations are either too easy or only focus on getting correct short answers. To address these issues, we present IMO-Bench, a suite of advanced reasoning benchmarks, vetted by a panel of top specialists and that specifically targets the level of the International Mathematical Olympiad (IMO), the most prestigious venue for young mathematicians. IMO-AnswerBench first tests models on 400 diverse Olympiad problems with verifiable short answers. IMO-Proof Bench is the next-level evaluation for proof-writing capabilities, which includes both basic and advanced IMO level problems as well as detailed grading guidelines to facilitate automatic grading. These benchmarks played a crucial role in our historic achievement of the gold-level performance at IMO 2025 with Gemini Deep Think (Luong and Lockhart, 2025). Our model achieved 80.0% on IMO-AnswerBench and 65.7% on the advanced IMO-Proof Bench, surpassing the best non-Gemini models by large margins of 6.9% and 42.4% respectively. We also showed that autograders built with Gemini reasoning correlate well with human evaluations and construct IMO-GradingBench, with 1000 human gradings on proofs, to enable further progress in automatic evaluation of long-form answers. We hope that IMO-Bench will help the community towards advancing robust mathematical reasoning and release it at https://imobench.github.io/.
Sponsored by Paperpile, the PDF & BibTeX manager trusted by top AI labs.
Get 30 days freeSummary
- The paper presents IMO-level benchmarks that assess both short-answer and full proof-writing abilities, vetted by experts.
- It develops robust autograders, with AnswerAutoGrader achieving 98.9% accuracy and ProofAutoGrader showing high Pearson correlations (0.93–0.96).
- The study reveals significant gaps in current LLM performance, setting new standards for rigorous multi-step reasoning evaluation.
Towards Robust Mathematical Reasoning: A Technical Analysis
Motivation and Benchmark Design
The paper addresses the limitations of existing mathematical reasoning benchmarks for LLMs, noting that datasets such as GSM8K, MATH, and AIME have reached saturation and primarily focus on short-answer correctness rather than rigorous multi-step reasoning. To overcome these deficiencies, the authors introduce a suite of benchmarks at the International Mathematical Olympiad (IMO) level, designed to evaluate both answer accuracy and proof-writing capabilities. The suite comprises three main components:
- IMO-AnswerBench: 400 robustified Olympiad problems with short, verifiable answers, spanning Algebra, Combinatorics, Geometry, and Number Theory, and stratified by difficulty.
- IMO-ProofBench: 60 proof-based problems (30 basic, 30 advanced), requiring full, rigorous solutions and graded on a 0–7 scale.
- IMO-GradingBench: 1000 human-graded solutions to advanced IMO-ProofBench problems, enabling evaluation of models' grading capabilities.
The problems are carefully paraphrased and modified to prevent memorization, with distractors and reformulations to ensure nontrivial reasoning is required. The benchmarks are vetted by IMO medalists and mathematicians, ensuring high-quality and diverse coverage.
Figure 1: Topic distribution by category in IMO-AnswerBench, highlighting the breadth of knowledge required, especially in Number Theory and Combinatorics.
Automated Grading Systems
A key technical contribution is the development of robust autograders for both short answers and proofs:
- AnswerAutoGrader: Utilizes Gemini 2.5 Pro to extract and semantically compare final answers, handling algebraic, numerical, and set equivalence. The autograder achieves near-human accuracy (98.9%) in answer verification, as demonstrated by confusion matrix analysis.
Figure 2: Confusion matrix for AnswerAutoGrader vs. human expert grades, showing high agreement over 840 solutions from 14 public models.
- ProofAutoGrader: Employs Gemini 2.5 Pro with detailed prompts including problem statement, candidate solution, reference solution, and grading guidelines. The autograder's scores exhibit high Pearson correlation ($0.93$–$0.96$) with human expert grades on both basic and advanced proof problems.
Figure 3: Correlation between ProofAutoGrader and human experts on advanced IMO-ProofBench, evaluated over 170 internal models.
Despite strong aggregate performance, the autograder is not a perfect substitute for human experts, occasionally missing high-level logical errors or being overly punitive for unconventional but correct solutions.
Model Performance and Robustness
The benchmarks reveal substantial gaps in current model capabilities:
- On IMO-AnswerBench, the Gemini IMO-gold model achieves 80.0% accuracy, outperforming the best non-Gemini model by 6.9% and the best open-weight model by 19.2%. Robustification consistently reduces model performance, confirming the effectiveness of the modifications in preventing memorization.
- On IMO-ProofBench (Advanced), the IMO-gold model scores 65.7%, while the best non-Gemini and open-weight models achieve only 23.3% and 7.1%, respectively. This demonstrates that answer accuracy does not imply robust reasoning, and that proof-writing remains a significant challenge.
Figure 4: Grade distribution for solutions in IMO-ProofBench by difficulty levels, illustrating the increasing proportion of incorrect and partial solutions at higher difficulty.
- On IMO-GradingBench, models struggle to accurately grade proofs, with the best accuracy at 54.0% and best MAE at 18.4%. The benchmark is intentionally challenging, providing only the problem and solution without reference answers or guidelines.
Figure 5: Grade distribution across examples in IMO-GradingBench, showing balanced correct and incorrect grades but significant variance per problem.
Implementation Details and Trade-offs
The autograders are implemented via prompt engineering on Gemini 2.5 Pro, with strict output protocols to ensure deterministic grading. For answer grading, the system focuses solely on final result equivalence, while proof grading requires step-by-step logical verification against detailed rubrics. The agentic framework for Gemini 2.5 Pro (Huang et al.) employs iterative self-verification and bug-fixing, with parallel runs to maximize solution quality.
Resource requirements are substantial, especially for proof grading, which necessitates large context windows and multiple model calls per solution. Human expert evaluation remains costly and is recommended for high-stakes assessments. The risk of future data contamination is noted, as public release of benchmarks may lead to their inclusion in training corpora, threatening benchmark integrity.
Implications and Future Directions
The results indicate that current frontier models, including GPT-5 and Gemini 2.5 Pro, are far from human-level performance in robust mathematical reasoning, particularly in proof-writing and grading. The benchmarks provide a rigorous testbed for future model development, emphasizing the need for deep, verifiable reasoning rather than mere answer-getting.
The release of IMO-Bench and its autograders is expected to shift community focus toward more advanced and reliable AI, with scalable evaluation tools that correlate strongly with human judgment. However, ongoing vigilance is required to prevent benchmark decay due to data contamination.
Theoretically, the work highlights the limitations of current LLM architectures in multi-step reasoning and the importance of explicit reasoning supervision. Practically, the benchmarks and autograders offer a pathway for systematic model evaluation and improvement, with potential applications in education, automated grading, and mathematical research.
Conclusion
The paper presents a comprehensive suite of IMO-level benchmarks and automated grading tools for robust evaluation of mathematical reasoning in LLMs. The results demonstrate that answer accuracy is insufficient for assessing true reasoning capabilities, and that proof-writing and grading remain open challenges. The benchmarks and autograders provide scalable, reliable methods for model evaluation, with strong correlation to human expert judgment. The work sets a new standard for mathematical reasoning evaluation and will drive future progress in AI toward deeper, more verifiable reasoning.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
Explaining “Towards Robust Mathematical Reasoning”
Overview
This paper is about making better, harder tests to see how well AI models can actually do math, not just guess answers. The authors build new, IMO-level benchmarks (the IMO is the International Mathematical Olympiad, a very tough contest for high school students) that check:
- Can a model get the right short answer?
- Can it write a full, correct proof?
- Can it grade someone else’s proof?
They use these tests to guide progress (“north-star metrics”) and show that strong models should be judged on their reasoning, not just their final answers.
What questions did the researchers ask?
The paper looks at simple, clear questions:
- Existing math tests for AI are getting too easy. So, what harder, fairer tests should we use?
- How can we check if a model understands math deeply (by writing proofs), not just tricks for guessing?
- Can we build automatic graders that score answers and proofs in a way that matches human experts?
- Do these tougher tests help improve AI models and reveal where they still struggle?
How did they do the paper?
Think of a “benchmark” like a well-designed sports competition where each game tests a different skill. The authors built three such competitions:
- IMO-AnswerBench (400 problems): Short-answer tasks across Algebra, Geometry, Number Theory, and Combinatorics, at four difficulty levels (from pre-IMO up to IMO-hard). They “robustified” problems so models can’t rely on memorization—by paraphrasing, changing names and numbers, or adding small twists—like rewriting a problem so the answer is a specific number rather than a “yes/no.”
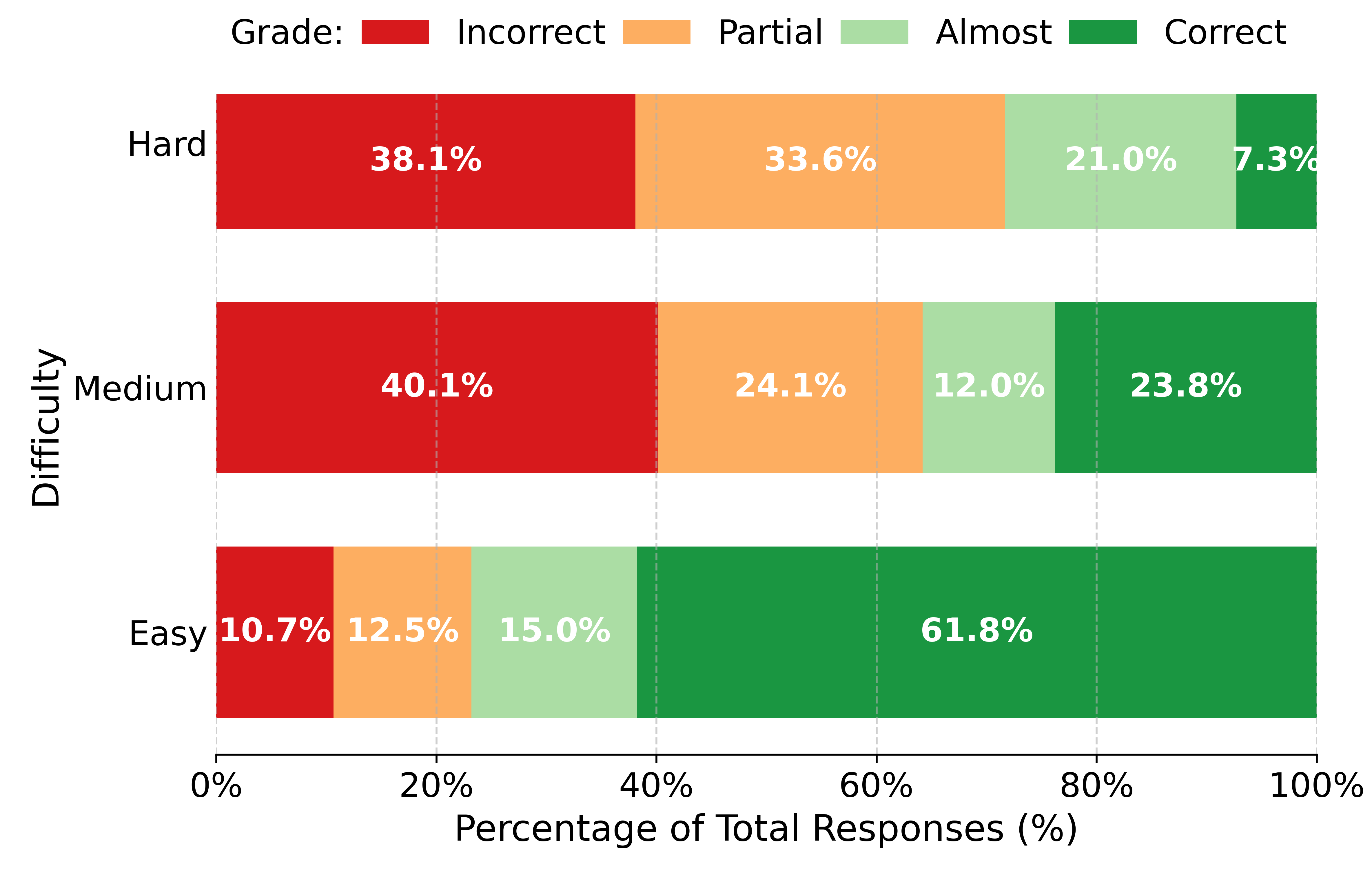
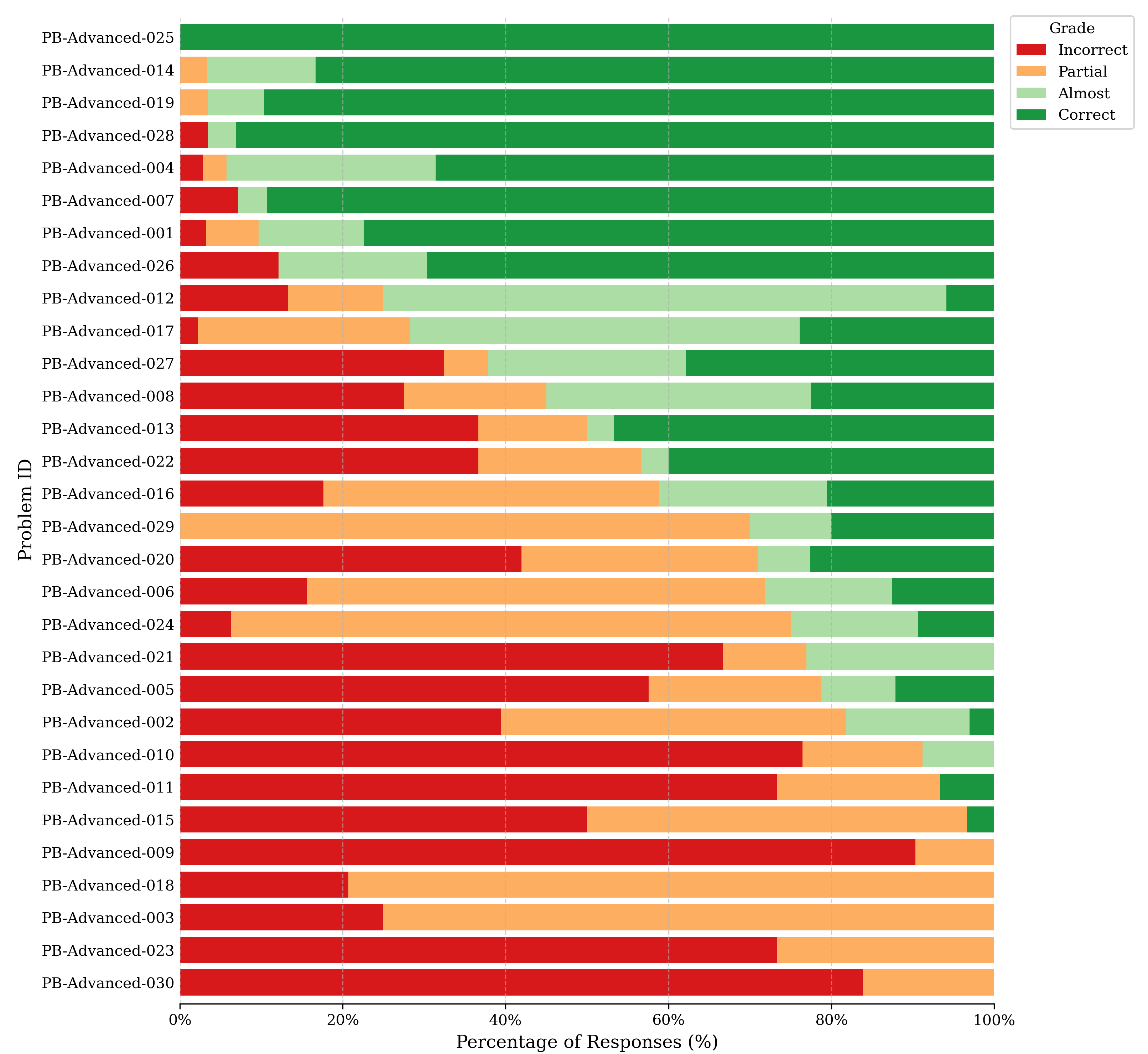
- IMO-ProofBench (60 problems): Proof-writing tasks where models must produce a complete, logical solution. These are split into Basic (easier to medium IMO level) and Advanced (hard, full IMO-style sets, including brand-new problems). Solutions are graded like the IMO, from 0 to 7 points, with simple categories:
- Correct (7), Almost (6), Partial (1), Incorrect (0)
- This focuses on how models reason, step by step.
- IMO-GradingBench (1000 graded examples): A dataset of problems, model-written solutions, and expert scores. It tests whether a model can look at a proof and grade it accurately without seeing an official answer.
They also built two “autograders”:
- AnswerAutoGrader: An AI tool that checks whether a model’s short answer matches the true answer, even if phrased differently. For example, “all real numbers except −4” should count the same as “(−∞, −4) ∪ (−4, ∞).”
- ProofAutoGrader: An AI tool that reads a proof and scores it using the same 0–7 style, with a reference solution and grading rules. It tries to mimic a human grader.
A key idea here is “correlation”: if the autograder’s scores rise and fall similarly to human scores across many models, that’s a strong sign it agrees with human judgment. They measure this with a number between 0 and 1 (closer to 1 means stronger agreement).
Main findings and why they matter
- Harder is better: When they “robustified” problems, model performance dropped across the board. This suggests some models were relying on memorized patterns rather than true reasoning. Making problems trickier helps reveal real ability.
- Short answers aren’t enough: Many models can get final answers but struggle to write correct, complete proofs. On the Advanced ProofBench, most non-Gemini models scored below 25% of the total possible points. That’s a big gap between “answer-getting” and “reasoning.”
- Strong model results: The authors’ Gemini Deep Think model performed very well:
- About 80% on IMO-AnswerBench (roughly 4 out of 5 problems correct)
- About 65.7% on Advanced IMO-ProofBench (close to 2 out of 3 points)
- These are large margins over other models tested. They say these benchmarks helped them reach gold-level performance at IMO 2025.
- Autograders work surprisingly well:
- AnswerAutoGrader matched human judgment almost perfectly (about 98.9% accuracy on correct answers).
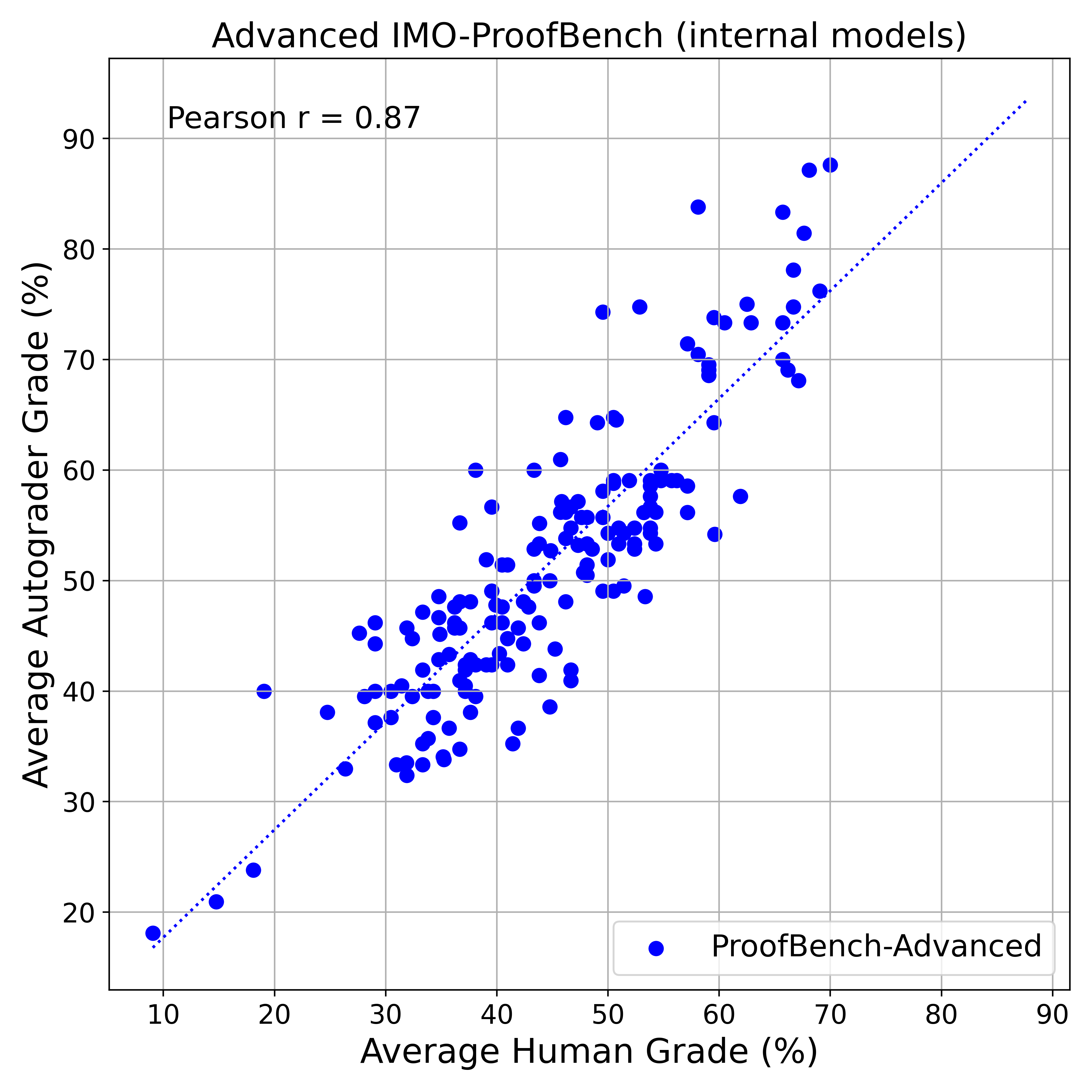
- ProofAutoGrader’s scores strongly tracked human scores (correlation around 0.93–0.96 on public models, and 0.87 on a larger internal set). It’s not perfect, but good enough to help the community test models more easily.
- Grading is hard without help: On IMO-GradingBench, where models must grade with minimal context, even top systems only reached around 54% accuracy. This shows grading proofs is a very tough skill, and structured guidance (like reference solutions) helps a lot.
Why this matters: These results prove that testing real mathematical reasoning needs more than checking final answers. Proof-writing and proof-grading are essential to see if a model truly understands math.
What’s the impact?
- Better goals for the field: These IMO-level benchmarks push AI beyond guessing and toward careful, step-by-step reasoning. They can become standard tests to track real progress.
- Scalable evaluation: Autograders make it possible to evaluate thousands of answers and proofs faster and cheaper, while still aligning closely with human experts. That’s helpful for researchers and developers.
- Honest difficulty: By focusing on hard, diverse problems and proof quality, the benchmarks reveal weaknesses in models that would be hidden by easier tests. This helps avoid “overfitting” (when a model looks good only on familiar data).
- Community resource: The suite (IMO-AnswerBench, IMO-ProofBench, IMO-GradingBench) is released at imobench.github.io so others can use it, compare models fairly, and build stronger reasoning systems.
- Still, use with care: Autograders aren’t perfect—they can miss high-level logical mistakes or penalize unusual but correct solutions. Human experts remain the gold standard for final judgments. There’s also a long-term risk that public benchmarks get memorized by future models, which can make scores less meaningful.
In short: This paper builds tougher, smarter tests for AI math ability, proves that proof-writing is the real challenge, and shows that automatic grading can closely match human experts. It helps shift the focus from “Did the model get the answer?” to “Did it reason correctly?”—a crucial step for creating truly reliable and intelligent systems.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a consolidated list of concrete gaps and unresolved questions that emerge from the paper, intended to guide future research.
- Benchmark scope and representativeness
- Limited domain coverage: focus is confined to Olympiad-style problems in Algebra, Combinatorics, Geometry, and Number Theory; no coverage of proof-heavy undergraduate/advanced topics (e.g., real analysis, abstract algebra, topology), applied math, or multi-disciplinary problems.
- Geometry short-answer bias: the AnswerBench geometry set skews toward angle/length computations, omitting many inherently proof-based geometry tasks that are central to Olympiad reasoning.
- Dataset scale: ProofBench includes only 60 problems (30 basic, 30 advanced), which may be insufficient for robust model ranking, ablations, or fine-grained progress tracking.
- Problem-source diversity: advanced ProofBench is heavily concentrated on a few competitions (USAMO 2025, IMO 2024, and 18 novel problems from contributors), leaving unclear generalization to other years, regions, or lesser-known contests.
- Robustification and contamination
- Robustification validity: no systematic, blinded human paper verifies that all robustified problems preserve equivalence, difficulty, and solution uniqueness; potential risk of accidental changes in problem semantics or difficulty.
- Robustification methodology transparency: the mix of manual and LLM-driven transformations is not fully characterized (error rates, types of transformations, quality control), nor are failure cases cataloged.
- Contamination audit: there is no empirical audit to rule out training data leakage in evaluated models (especially for USAMO/IMO problems); observed overperformance on USAMO vs. novel problems suggests possible exposure but is not quantified.
- Long-term benchmark decay: while future contamination is acknowledged, no concrete mitigation plan (e.g., sequestered test servers, data poisoning detection, watermarking, or legal/robots.txt constraints) is proposed.
- Evaluation design and reproducibility
- Human grading reliability: inter-rater reliability (e.g., Cohen’s kappa, Krippendorff’s alpha, ICC) is not reported; the effect of grader expertise variance, calibration, and rubric interpretation on scores is unknown.
- Grading granularity: mapping to {Correct (7), Almost (6), Partial (1), Incorrect (0)} compresses nuance (e.g., a high partial vs. a minimal partial); no analysis of how this affects model ranking stability or error analysis.
- Run-to-run variance: although some results are averaged over 8 samples, confidence intervals and statistical significance testing are missing; decoding settings (temperature, nucleus sampling) and their effects on variance are under-specified.
- Tool-use parity: evaluation does not clearly standardize or disclose tool/toolchain allowances (e.g., calculators, CAS, diagram tools), context windows, or token budgets, which may confound cross-model comparisons.
- Service instability bias: aborted evaluations (e.g., due to API instability) introduce selection bias; no protocol for handling missing or partial results is specified.
- Prompt and reference solution dependence: proof grading uses provided reference solutions; the impact of reference-solution style/coverage on autograder and human grades is not quantified.
- Autograder validity and limitations
- Answer autograder coverage: near-human accuracy is reported on a subset; robustness to adversarially formatted outputs, multilingual answers, unit conventions, implicit intervals, symbolic equivalences, or composite-set answers is not systematically tested.
- Proof autograder failure modes: known weaknesses include missing high-level logical errors and penalizing unconventional but valid proofs; no taxonomy, frequency analysis, or targeted stress tests for these failure modes are provided.
- Calibration and bias: correlations (Pearson) are reported, but absolute error, grade bias (over-/under-scoring), and rank-order robustness (e.g., Kendall’s tau) across models and topics are not analyzed.
- Minimal-context grading (GradingBench) gap: large performance drop from ProofBench autograder to per-instance GradingBench suggests context dependence; methods to close this gap (e.g., better graders without references) remain unexplored.
- Generality beyond Gemini: autograders are built on Gemini 2.5 Pro; portability, reproducibility with open models, and susceptibility to Goodharting (optimizing for the grader rather than correctness) are not assessed.
- Task design constraints and blind spots
- Short-answer reformulations: AnswerBench often reformulates tasks to produce unique numeric targets; this excludes central Olympiad question types (existence, construction, yes/no) and may incentivize “answer-getting” strategies despite the paper’s goals.
- Lack of step-level verification: there is no stepwise, localized error identification for proofs (e.g., verifying each inference), limiting diagnosis and targeted training (despite citing step verification literature).
- Diagram/visual reasoning: geometry evaluations rely on text; no support for figures or construction steps, potentially underestimating geometry reasoning and missing a key mode of Olympiad problem-solving.
- Time/compute realism: evaluations do not emulate IMO constraints (time limits, attempts, reflective revisions); no analysis of compute/latency accuracy trade-offs or adaptive test-time strategies.
- Analysis depth and diagnostics
- Sparse error analysis: beyond aggregate accuracy and a few category-level trends, there is limited breakdown of error types (e.g., combinatorial invariants, inequalities, extremal arguments, parity) that would guide method development.
- Overfitting detection: while overperformance on USAMO vs. novel problems is observed, there is no systematic metric or protocol for detecting dataset-specific overfitting or solution-style overfitting.
- Topic-level autograder reliability: autograder agreement by topic/difficulty is not reported; it is unclear if certain domains (e.g., combinatorics) are systematically misgraded.
- Dataset construction and release details
- GradingBench composition: solutions come from model generations; the diversity of solution styles is likely limited, and the absence of human-written and adversarially crafted proofs may limit the grader’s generalization.
- Class balancing: GradingBench is roughly balanced across categories; this may distort real-world grade distributions and complicate model calibration for naturally skewed settings.
- Licensing/copyright constraints: the paper does not detail licensing for problem statements/solutions and whether some content is omitted or paraphrased due to copyright, which affects reproducibility.
- Missing multilingual variants: benchmarks are English-only; the effect of translation or multilingual evaluation on both solvers and graders remains unknown.
- Training and benchmarking methodology
- Interaction protocols: multi-turn reasoning, reflection, and self-correction strategies are not standardized across models; their impact on performance and comparability is unclear.
- Hyperparameter disclosure: decoding and retry policies are not fully specified; fairness in resource allocation (tokens, retries, parallel calls) across proprietary models is opaque.
- External tool integration: no controlled experiments assess the benefit of external tools (e.g., SMT solvers, CAS, formal proof assistants), despite their relevance for rigorous verification.
- Open directions for improving evaluation
- Better anti-Goodharting design: mechanisms to discourage “grading to the grader” (e.g., adversarial grader tests, grader ensembles, randomized rubrics, hidden rubric variants) are not proposed.
- Robustification QA: introduce blinded human panels to certify equivalence and difficulty retention post-robustification; report agreement and error corrections.
- Inter-rater and rubric studies: quantify grader agreement, conduct rubric sensitivity analyses, and publish guidelines for harmonizing 0–7 versus 4-bin mappings.
- Step-level and formal verification: incorporate step-by-step verification datasets and explore hybrid informal–formal pipelines (e.g., Lean/Isabelle integration) to close the gap between natural-language reasoning and formal correctness.
- Confidence and deferral: develop and evaluate uncertainty-aware graders that know when to defer to human experts; report selective-risk trade-offs.
- Longitudinal contamination checks: establish periodic revalidation protocols (e.g., canary problems, new sequestered items, provenance tracking) to monitor benchmark freshness.
- External validity and generalization
- Transfer beyond Olympiads: no evidence that gains on these benchmarks translate to research-style proofs, undergraduate coursework, or non-contest mathematical tasks.
- Cross-lingual and cross-format robustness: effects of language, notation variants, and alternative encodings (e.g., LaTeX-heavy, handwritten, OCR) are unexplored.
These gaps suggest concrete next steps: expand and diversify the problem sets (including diagrams and non-numeric goals), rigorously validate robustifications, standardize and disclose evaluation protocols, measure inter-rater reliability, deepen autograder diagnostics and calibration, add step-level verification, audit contamination, and design anti-Goodharting safeguards for grader-driven development.
Practical Applications
Below is an overview of practical, real-world applications that follow directly from the paper’s benchmarks, autograding methods, and evaluation findings. Items are grouped by deployment horizon and connected to sectors, with concrete tools/workflows and feasibility notes.
Immediate Applications
These can be deployed now with modest integration and guardrails, using the released benchmarks and the demonstrated LLM-as-judge autograders.
Academia and Education
- Olympiad training and practice at scale (Education)
- What: Use IMO-AnswerBench and IMO-ProofBench to power adaptive practice, proof-writing drills, and realistic “mock IMO” exams with human-aligned scoring.
- Tools/workflows: LMS plugins (Canvas, Moodle) that (a) assign robustified problems; (b) accept proof-style responses; (c) grade via ProofAutoGrader; (d) surface rubric-aligned feedback (Correct/Almost/Partial/Incorrect, 0–7 mapping).
- Assumptions/dependencies: Access to a reliable judge model (e.g., Gemini 2.5 Pro); rubric+reference solution availability for each task; human spot-checks for edge cases.
- Autograding of university STEM proofs and problem sets (Education)
- What: Instructors upload problem statements, references, and rubrics; students submit proofs; the system provides preliminary scores and feedback, flagging uncertain cases for TA review.
- Tools/workflows: “Proof Grader Assistant” integrated into LMS; batch grading pipelines with per-problem confidence thresholds.
- Assumptions/dependencies: Human oversight remains required; domain shift beyond Olympiad math reduces grading reliability without tuned rubrics.
- Course and curriculum evaluation of reasoning outcomes (Education, Academic Assessment)
- What: Use IMO-GradingBench to benchmark cohorts’ proof quality over time and evaluate interventions (new textbooks, teaching methods).
- Tools/workflows: Cohort-wide pre/post testing, aggregated correlation reports, difficulty-stratified dashboards.
- Assumptions/dependencies: Statistical validity depends on adequate sample sizes and balanced difficulty sets.
Industry (Software, AI, Data/Model Evaluation)
- Reasoning QA for model development and regression testing (Software/AI)
- What: Adopt the suite as “north-star” metrics for internal LLM training cycles; add robustified tasks to catch overfitting and answer-guessing.
- Tools/workflows: Continuous evaluation (EvalOps) pipelines with AnswerAutoGrader and ProofAutoGrader; release gates keyed to proof-level metrics, not just final answers.
- Assumptions/dependencies: Continued access to benchmarks not in the training set; tracking of contamination; compute budget for multi-seed evaluations.
- LLM-as-judge components in evaluation stacks (Software/AI)
- What: Port the paper’s judge prompts and scoring rubric to score long-form reasoning across domains (math today, other reasoning tasks next).
- Tools/workflows: “Generalized Judge Service” microservice that accepts problem, candidate solution, reference, and rubric; returns graded outcomes + rationales.
- Assumptions/dependencies: Correlation to humans demonstrated strongest in math; domain adaptation requires high-quality references and tailored rubrics.
- Reward-model bootstrapping from human-aligned grades (Software/AI)
- What: Use IMO-GradingBench (1000 graded solutions) to train or calibrate reward models that prefer rigorous, logically consistent reasoning traces.
- Tools/workflows: Offline preference modeling; RLHF/RLAIF pipelines seeded with human-graded proof data.
- Assumptions/dependencies: Dataset license compliance; generalization from Olympiad proofs to other domains is nontrivial.
- Benchmark hardening and leakage testing (Software/AI, MLOps)
- What: Apply the paper’s robustification techniques (paraphrasing, distractors, numeric changes) to internal eval sets to prevent shortcut learning and detect memorization.
- Tools/workflows: “Robustify-then-Score” workflow with original vs. perturbed performance diffs; leakage monitors.
- Assumptions/dependencies: Requires SMEs or trusted LLMs to generate valid perturbations without altering problem intent.
Policy and Standards
- Procurement/evaluation criteria for public-sector AI (Policy, Standards)
- What: Require vendors to report proof-level reasoning metrics (e.g., ProofBench scores) and show that outputs are not just correct answers but defensible arguments.
- Tools/workflows: RFP templates referencing proof-based evaluation; minimum correlation thresholds with expert graders.
- Assumptions/dependencies: Benchmarks primarily math-focused; transposition to other policy-relevant domains needs tailored rubrics and references.
- Safety guardrails via rationale verification (Policy, Safety)
- What: Use a proof-judging step to screen long-form rationales for logical gaps before model outputs are shown to end users.
- Tools/workflows: “Rationale Gate” in deployment stacks; escalate uncertain/low-confidence cases to humans.
- Assumptions/dependencies: Human-in-the-loop for high-stakes contexts; false positives/negatives must be tracked.
Daily Life and Consumer Apps
- Rigorous AI math tutors for self-learners and Olympiad aspirants (Education, Consumer)
- What: Tutors that score full solutions, explain deductions, and point to missing lemmas or unjustified steps.
- Tools/workflows: Mobile/web apps embedding AnswerAutoGrader + ProofAutoGrader; paper plans based on topic-level weaknesses.
- Assumptions/dependencies: Clear UI for uncertainty and partial credit; protection against feedback hallucinations by referencing standard solutions.
- Community contest platforms with fair, scalable grading (Education, Nonprofit)
- What: Host regional/national contests with automatic preliminary grading, reducing burden on finite expert judges.
- Tools/workflows: Contest backend that ingests submissions, auto-scores, and queues contentious cases for human adjudication.
- Assumptions/dependencies: Clear appeals process; published rubrics; audit logs for transparency.
Long-Term Applications
These require further research, domain adaptation, scaling, or governance to realize reliably.
Cross-Domain Reasoning and Verification
- Domain-general “proof” graders for STEM and beyond (Healthcare, Law, Engineering, Finance)
- What: Extend the proof-grading paradigm to clinical rationales, legal arguments, engineering design justifications, and investment theses.
- Tools/workflows: Domain-specific references, rubrics, and ontology-aware graders; integration into EHR decision support, contract analysis, spec reviews, and investment memos.
- Assumptions/dependencies: High-quality, domain-specific gold references; rigorous validation against domain experts; liability and compliance frameworks.
- Certified reasoning layers for agentic systems (Robotics, Autonomous Systems, Software Agents)
- What: Agents produce plans alongside proofs-of-correctness-like rationales that a grader validates before execution.
- Tools/workflows: “Plan+Proof” pipelines; graded checkpoints; risk-gated execution policies.
- Assumptions/dependencies: Scalable, real-time grading; robust detection of subtle logical flaws; fallback strategies.
Education at Scale and Assessment Reform
- Accreditation-grade automated assessment of mathematical writing (Education Policy)
- What: National or international exams that accept free-form proofs with audited automated graders, reducing inequities in access to human graders.
- Tools/workflows: Multi-grader ensembles, calibration against expert panels, bias and reliability reporting, randomized audits.
- Assumptions/dependencies: Extensive field validation; public confidence in grading fairness; data privacy for student work.
- Personalized mastery learning with rigorous reasoning checks (Education)
- What: Longitudinal evaluation of a learner’s ability to argue correctly, not just compute answers, spanning K–12 to higher ed.
- Tools/workflows: Reasoning portfolios; skill graphs linking sublemma proficiency; targeted feedback loops; teacher dashboards.
- Assumptions/dependencies: Content authoring at scale; teacher adoption; integration with existing standards.
AI Safety, Governance, and Standards
- Reasoning compliance standards for high-stakes AI (Policy, Safety)
- What: Require models to pass proof-style verification layers in regulated domains (e.g., medication changes, tax decisions, structural calculations).
- Tools/workflows: “Reasoning Trace Compliance” checklists; third-party certification services benchmarking models with robustified tasks.
- Assumptions/dependencies: Cross-sector agreement on acceptable rubrics; mechanisms to prevent benchmark contamination; periodic refresh with hidden/narrow-release items.
- Continually refreshed, contamination-resistant benchmarks (AI Governance)
- What: Rotation of private/narrowly shared problem sets with systematic robustification and post-hoc leakage detection to preserve validity over time.
- Tools/workflows: Secure item banks; watermarking or cryptographic item tracing; performance drift monitors.
- Assumptions/dependencies: Sustainable governance body; contributor pipelines; legal and ethical data practices.
Model Training and Tooling
- Training models to internalize rigorous reasoning (Software/AI)
- What: Use proof-graded signals (0–7, Correct/Almost/Partial/Incorrect) to shape models that argue well, not just answer well (e.g., RL from rubric).
- Tools/workflows: Multi-objective training that rewards both correctness and rigor; curriculum learning from basic to advanced proof sets.
- Assumptions/dependencies: Avoiding overfitting to public benchmarks; generating diverse, novel problems and references; computational cost.
- IDE and notebook “proof lens” for algorithmic development (Software Engineering)
- What: Developers supply invariants and mini-proofs for algorithms; a grader flags missing steps or contradictions in English+code hybrids.
- Tools/workflows: VS Code/Jupyter extensions; spec-to-proof prompts; links to formal tools where feasible.
- Assumptions/dependencies: Bridging informal to formal reasoning; developer ergonomics; alignment with formal verification where needed.
Finance and Enterprise Decision Support
- Audit trails for rationale-backed decisions (Finance, Enterprise Risk)
- What: Investment or policy memos must pass a rationale grader that checks for logical completeness, stated assumptions, and consistent use of evidence.
- Tools/workflows: Decision “check-and-submit” workflows; exception queues; periodic human audits.
- Assumptions/dependencies: Tailored rubrics; explainability expectations; acceptance by compliance teams.
Key feasibility notes across applications:
- Human oversight remains essential in high-stakes settings; the paper shows strong but imperfect correlation between autograders and expert judgment.
- Domain transfer requires domain-specific reference solutions and carefully designed rubrics; math results do not automatically generalize.
- Benchmark contamination risk grows after public release; long-term validity demands rotating, robustified, and partially private items.
- Cost and latency of LLM-as-judge evaluations must be managed via batching, confidence thresholds, and selective human review.
Glossary
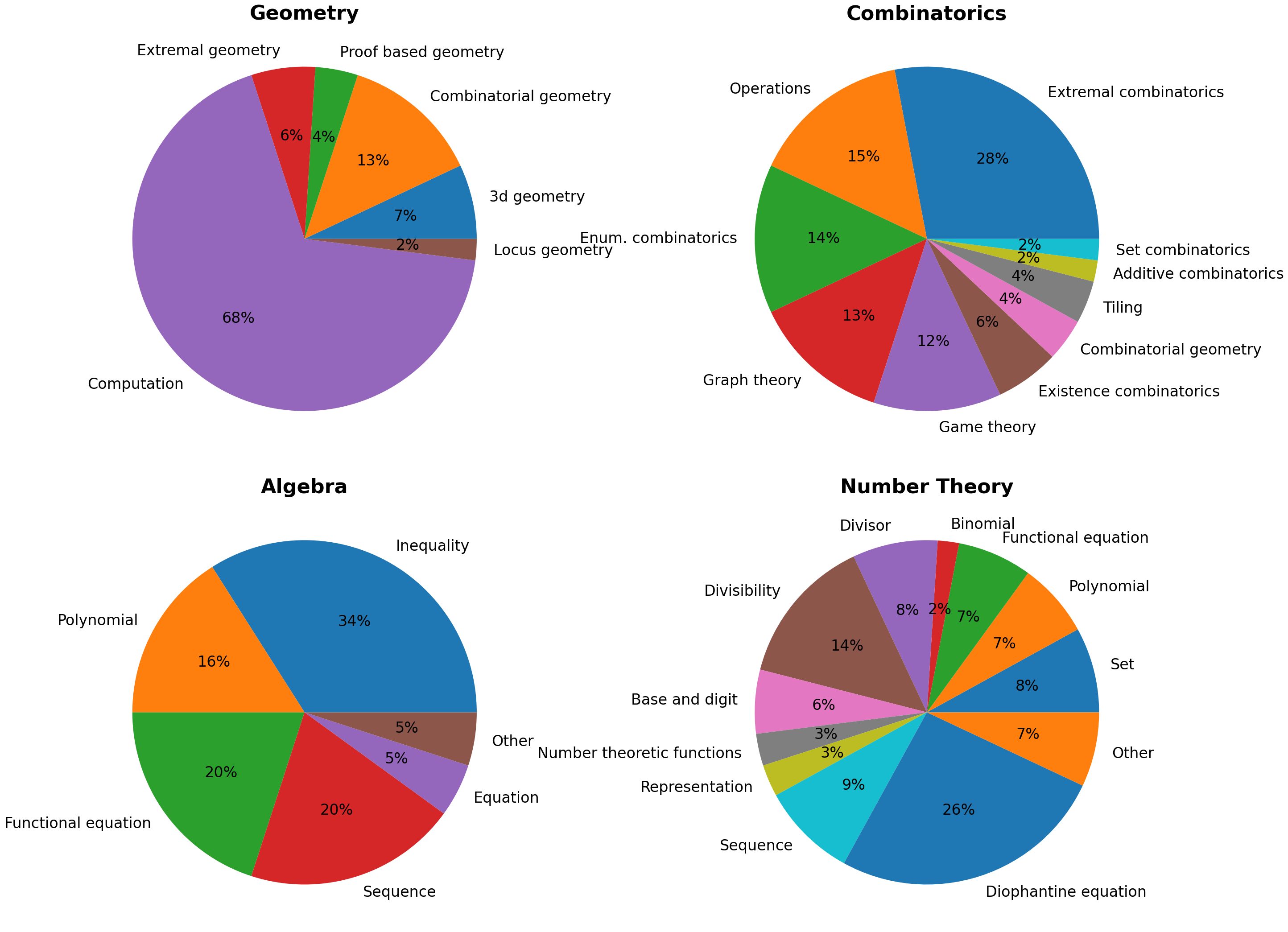
- Additive Combinatorics: A branch of combinatorics focused on the additive properties of sets and the structure of sumsets. "Additive Combinatorics, Set Combinatorics, Tiling, Combinatorial Geometry, Operations (problems involving operations, often requiring finding invariant or monovariant properties), and Game Theory."
- Agentic framework: An orchestration approach that uses tools and multiple model calls to accomplish tasks, rather than a single inference. "Gemini 2.5 Pro with (Huang is an agentic framework rather than a single model call"
- Algebraic Number Theory: The paper of algebraic structures related to integers, such as number fields and rings of integers. "advanced topics such as Algebraic Number Theory."
- Autograder: An automated system that evaluates the correctness and quality of answers or proofs. "The autograder leverages Gemini 2.5 Pro, providing it with a prompt containing the problem statement, the candidate solution, a reference solution, and specific grading guidelines"
- Circumcircle: The unique circle passing through all vertices of a triangle. "such that the circumcircle of triangle is tangent to line ."
- Confusion matrix: A table summarizing classification performance across predicted vs. true labels. "Confusion matrix for vs. human expert grades, over 840 solutions generated by 14 public models (See Table~\ref{tab:imo-proof-bench-manual-result})."
- Data contamination: The process by which benchmark data is inadvertently incorporated into training datasets, compromising evaluation integrity. "The second limitation is the risk of long-term data contamination."
- Diophantine equations: Polynomial equations where integer solutions are sought. "spanning various topics such as Diophantine equations, divisibility problems, polynomials, sequence problems, functional equation problems on the set of integer, existence problems, problems involving arithmetic functions"
- Enumerative Combinatorics: The area of combinatorics concerned with counting the number of combinatorial structures. "covering Graph Theory, Enumerative Combinatorics (combinatorial counting problems), Extremal Combinatorics, Existence Combinatorics"
- Extremal Combinatorics: The paper of maximal or minimal sizes of structures that satisfy certain properties. "covering Graph Theory, Enumerative Combinatorics (combinatorial counting problems), Extremal Combinatorics"
- Foundation models: Large, general-purpose AI models trained on broad data and adaptable to many tasks. "Finding the right north-star metrics is highly critical for advancing the mathematical reasoning capabilities of foundation models"
- Frontier models: The strongest, most advanced AI models available at a given time. "The low performances of latest frontier models such as GPT-5 and on the advanced underscore the difficulty of advanced mathematical reasoning"
- Game Theory: The mathematical paper of strategic interaction among rational agents. "Additive Combinatorics, Set Combinatorics, Tiling, Combinatorial Geometry, Operations (problems involving operations, often requiring finding invariant or monovariant properties), and Game Theory."
- Graph Theory: The paper of graphs, which model pairwise relations between objects. "covering Graph Theory, Enumerative Combinatorics (combinatorial counting problems), Extremal Combinatorics"
- Grading guidelines: Prescriptive criteria used to assess the quality and correctness of solutions. "a reference solution, and specific grading guidelines (see Appendix \ref{subsec:autograder-prompt})."
- International Mathematical Olympiad (IMO): The premier international high school mathematics competition. "the International Mathematical Olympiad (IMO), the world's most celebrated arena for young mathematicians."
- IMO-AnswerBench: A benchmark of 400 robust, short-answer Olympiad problems for evaluating solution accuracy. "Our model achieved 80.0\% on IMO-AnswerBench and 65.7\% on the advanced IMO-ProofBench"
- IMO-GradingBench: A benchmark of 1000 solutions with human-assigned grades for evaluating proof-grading ability. "IMO-GradingBench"
- IMO-ProofBench: A proof-writing benchmark of 60 Olympiad-level problems with detailed grading. "The advanced IMO-ProofBench is much more challenging."
- Incircle: A circle inscribed in a triangle, tangent to all three sides. "segment intersect the incircle of triangle at point ."
- Incenter: The point where the internal angle bisectors of a triangle meet; the center of the incircle. "Let be a triangle with incenter ."
- Invariant: A quantity that remains unchanged under a given set of operations. "finding invariant or monovariant properties"
- Locus: The set of points that satisfy a given geometric condition. "spanning subcategories such as angle and sidelength computation, locus problems, and proof-based geometry problems"
- Mean Absolute Error (MAE): The average absolute difference between predicted and true values. "Mean Absolute Error (MAE) -- model-predicted categories are converted from {\it (Correct, Almost, Partial, Incorrect)} to IMO scores (7, 6, 1, 0)"
- Monovariant: A quantity that changes in a single direction (e.g., non-increasing) under operations, used to prove termination or impossibility. "finding invariant or monovariant properties"
- North-star metrics: Guiding, primary metrics that steer long-term development and evaluation. "Finding the right north-star metrics is highly critical for advancing the mathematical reasoning capabilities of foundation models"
- Overfitting: A model’s tendency to perform well on specific training-like data but poorly on novel data due to memorization of patterns. "suggesting potential overfitting in certain models."
- Pearson correlation coefficient: A measure of the linear relationship between two variables. "yielding high Pearson correlation coefficients of $0.96$ and $0.93$"
- Pre-IMO: A difficulty tier below IMO level, typically middle-school or pre-competition problems. "pre-IMO (middle school or pre-Math Olympiad problems)"
- Reference solution: An authoritative solution used to compare and grade candidate solutions. "the candidate solution, a reference solution, and specific grading guidelines"
- Robustification: Systematic modification of problems to prevent memorization and improve evaluation reliability. "robustification leads to a consistent drop in performance across all models."
- SymPy: A Python library for symbolic mathematics used to represent mathematical objects programmatically. "mathematical objects that can be expressed as SymPy objects."
- Tiling: Covering a plane or region with shapes without gaps or overlaps, studied in combinatorics. "Additive Combinatorics, Set Combinatorics, Tiling, Combinatorial Geometry"
- Triangle inequalities: Conditions on side lengths ensuring a valid triangle: each side is less than the sum of the other two. "triangle inequalities , , and ."
- TST (Team Selection Test): A national exam used to select students for international math competitions. "Another example is a combinatorics problem from USA TST 2005."
- USAMO (United States of America Mathematical Olympiad): A national high-school mathematics competition in the U.S. "6 directly from USAMO 2025."
Collections
Sign up for free to add this paper to one or more collections.