Efficient Curvature-aware Graph Network (2511.01443v1)

Abstract: Graph curvature provides geometric priors for Graph Neural Networks (GNNs), enhancing their ability to model complex graph structures, particularly in terms of structural awareness, robustness, and theoretical interpretability. Among existing methods, Ollivier-Ricci curvature has been extensively studied due to its strong geometric interpretability, effectively characterizing the local geometric distribution between nodes. However, its prohibitively high computational complexity limits its applicability to large-scale graph datasets. To address this challenge, we propose a novel graph curvature measure--Effective Resistance Curvature--which quantifies the ease of message passing along graph edges using the effective resistance between node pairs, instead of the optimal transport distance. This method significantly outperforms Ollivier-Ricci curvature in computational efficiency while preserving comparable geometric expressiveness. Theoretically, we prove the low computational complexity of effective resistance curvature and establish its substitutability for Ollivier-Ricci curvature. Furthermore, extensive experiments on diverse GNN tasks demonstrate that our method achieves competitive performance with Ollivier-Ricci curvature while drastically reducing computational overhead.

• The paper introduces Effective Resistance Curvature as a computationally efficient alternative to the complex Ollivier-Ricci measure.
• It integrates curvature-based adjustments into message passing and graph convolution to boost node classification and pooling performance.
• Experimental results demonstrate over 1300x speedup and improved scalability in large-scale graph representation learning.

Efficient Curvature-aware Graph Network

Graph Neural Networks (GNNs) have increasingly attracted attention due to their ability to capture complex node relationships and graph structures. Traditional GNNs, however, struggle with interpretability and efficiency, particularly at scale. This paper introduces an innovative solution by integrating geometric priors through graph curvature, leveraging the newly proposed Effective Resistance Curvature.

Introduction

The need for increasing interpretability and efficiency in Graph Neural Networks led to the exploration of geometric properties derived from graph curvature. In graph structures, Ollivier-Ricci curvature has traditionally been used to illustrate local geometric distributions between nodes. Despite its strong theoretical foundation and interpretability, the Ollivier-Ricci curvature is computationally intensive, making it impractical for large graphs. This paper addresses this limitation with the introduction of Effective Resistance Curvature, a novel metric grounded in the concept of modeling graphs as electrical circuits where resistance measures connectivity strength.

Effective Resistance Curvature

Effective Resistance Curvature leverages the concept of effective resistance in electrical circuits, modeling graph edges as resistors. In this way, the curvature reflects the ease of message passage between nodes, capturing the geometric structure similarly to Ollivier-Ricci but at lower computational cost. Crucially, effective resistance curvature is analytically shown to be a viable and efficient substitute for Ollivier-Ricci curvature.

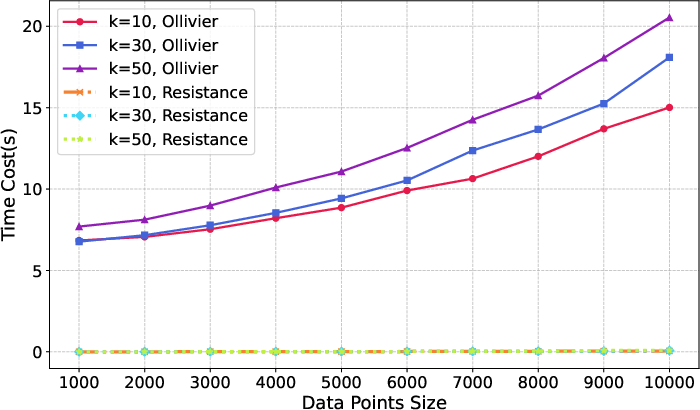
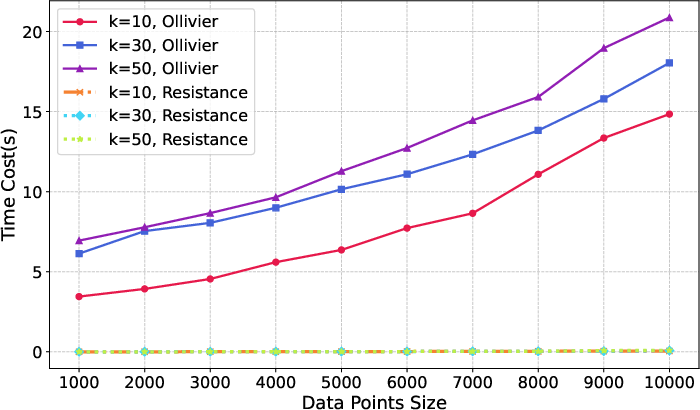
Figure 1: Time cost comparison for Ollivier-Ricci and effective resistance curvature on NW(upper) and RR (lower) graph.

Curvature-aware Graph Neural Networks

The integration of curvature into GNNs is proposed through two mechanisms:

1. Message Passing: Adapting the conventional GCN feature aggregation process by integrating curvature-based edge weight adjustments.
2. Graph Convolution: Utilizing effective resistance curvature to refine the graph convolution operation, optimizing node information accuracy and reducing interference from irrelevant nodes.

Theoretical Analysis

The paper performs an in-depth theoretical examination of Effective Resistance Curvature alongside Ollivier-Ricci. It is proven that effective resistance curvature accurately reflects node distribution and retains computational efficiency by avoiding complex optimal transport computations inherent to Ollivier-Ricci.

Experimental Evaluation

Graph Representation Learning

Experiments on real-world datasets demonstrated that methods integrating Effective Resistance Curvature consistently outperformed traditional curvature implementations in node classification and graph pooling tasks, achieving competitive performance while drastically reducing computational overhead.

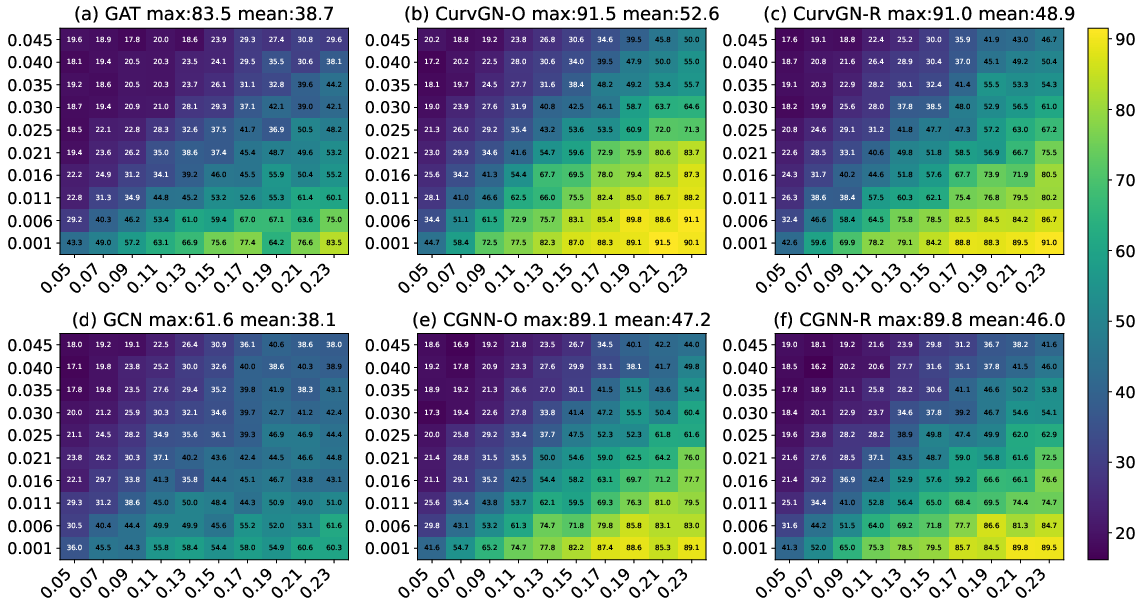
Figure 2: Classification accuracy heatmaps on SBM-generated graphs. (a,d): GAT/GCN baselines; (b,c,e,f): CurvGN/CGNN with Ollivier-Ricci (-O) and resistance (-R) curvature. (Axes: parameter p vs. parameter q)

Efficiency Comparison

Practical evaluations display a significant runtime reduction, highlighting that effective resistance curvature dramatically accelerates computation rates compared to Ollivier-Ricci, evidenced by speedup ratios exceeding 1300x in large-scale graphs.

Empirical Analysis

Further empirical analysis elucidated divergences in graph structure identification, with resistance curvature offering refined detection of bottlenecks in networks.

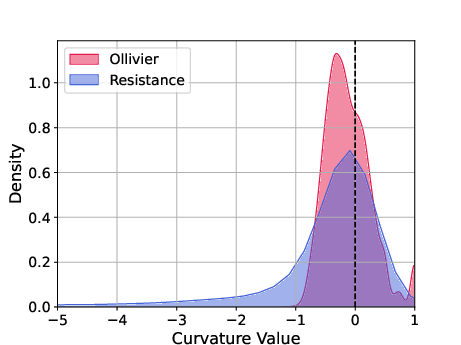
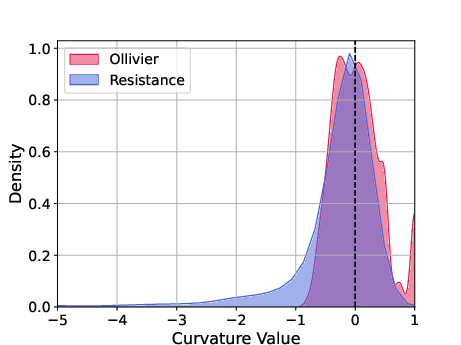
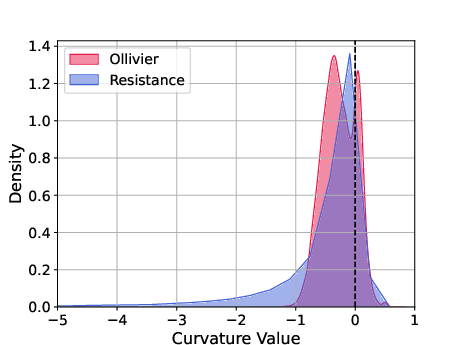
Figure 3: Curvature distribution KDE on three real-world dataset(left: Cora, center: Citeseer, right: PubMed)

Conclusion

This paper presents Effective Resistance Curvature as an efficient alternative to Ollivier-Ricci curvature, effectively capturing graph geometry in a computationally feasible manner for GNNs. The results confirm its competitive performance across various graph-centric tasks, making it suitable for large-scale applications while also improving interpretability through vectorized geometric insights. This approach not only advances theoretical understanding but also enriches practical GNN architectures with enhanced scalability and interpretational depth.