A roadmap for curvature-based geometric data analysis and learning (2510.22599v1)

Published 26 Oct 2025 in cs.LG and math.DG

Abstract: Geometric data analysis and learning has emerged as a distinct and rapidly developing research area, increasingly recognized for its effectiveness across diverse applications. At the heart of this field lies curvature, a powerful and interpretable concept that captures intrinsic geometric structure and underpins numerous tasks, from community detection to geometric deep learning. A wide range of discrete curvature models have been proposed for various data representations, including graphs, simplicial complexes, cubical complexes, and point clouds sampled from manifolds. These models not only provide efficient characterizations of data geometry but also constitute essential components in geometric learning frameworks. In this paper, we present the first comprehensive review of existing discrete curvature models, covering their mathematical foundations, computational formulations, and practical applications in data analysis and learning. In particular, we discuss discrete curvature from both Riemannian and metric geometry perspectives and propose a systematic pipeline for curvature-driven data analysis. We further examine the corresponding computational algorithms across different data representations, offering detailed comparisons and insights. Finally, we review state-of-the-art applications of curvature in both supervised and unsupervised learning. This survey provides a conceptual and practical roadmap for researchers to gain a better understanding of discrete curvature as a fundamental tool for geometric understanding and learning.

Summary

The paper presents a comprehensive framework unifying discrete curvature models to analyze non-Euclidean data structures.
It introduces a computational pipeline that selects appropriate data representations, computes curvature, and extracts geometric features.
Curvature-based approaches are demonstrated to enhance community detection, manifold learning, and graph neural network performance.

Curvature-Based Geometric Data Analysis and Learning: A Comprehensive Roadmap

Introduction

This work provides a systematic and technically rigorous review of discrete curvature models for geometric data analysis and learning, with a focus on their mathematical foundations, computational formulations, and applications in machine learning. The survey addresses the need for a unified framework to understand and apply curvature-driven methods to non-Euclidean data representations, such as graphs, simplicial complexes, cubical complexes, and point clouds. The authors present a detailed taxonomy of discrete curvature notions, discuss their theoretical motivations from Riemannian and metric geometry, and propose a computational pipeline for extracting geometric features from data. The review further synthesizes state-of-the-art applications in community detection, manifold learning, and geometric deep learning, particularly in the context of graph neural networks (GNNs).

Mathematical Foundations of Discrete Curvature

The paper delineates the transition from classical Riemannian curvature—sectional, Ricci, and scalar—to discrete analogues suitable for combinatorial and metric spaces. The principal discrete Ricci curvature models are:

Forman-Ricci Curvature: A combinatorial analogue based on the Bochner-Weitzenböck formula, applicable to cell complexes, graphs, and simplicial complexes. For unweighted graphs, the curvature of an edge $e = (v_1, v_2)$ simplifies to $\kappa_F^\#(e) = 4 - \deg(v_1) - \deg(v_2)$ , directly encoding local connectivity.
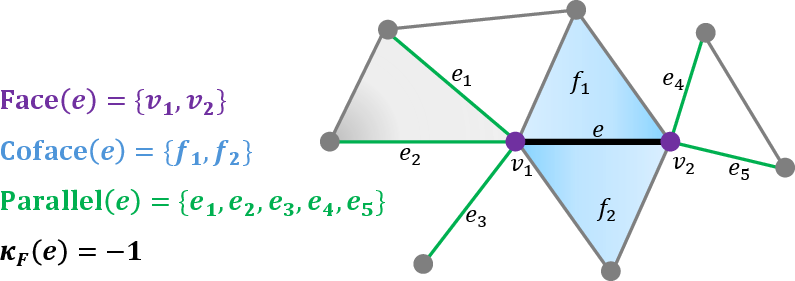
Figure 1: Computation of Forman-Ricci curvature for an edge in an unweighted simplicial complex, illustrating the roles of faces, cofaces, and parallel edges.
Ollivier-Ricci Curvature: Defined via optimal transport between probability measures on the neighborhoods of adjacent vertices, capturing the deviation from flatness in terms of Wasserstein distance. This is the only discrete Ricci curvature known to converge to the Riemannian Ricci curvature in the manifold limit.
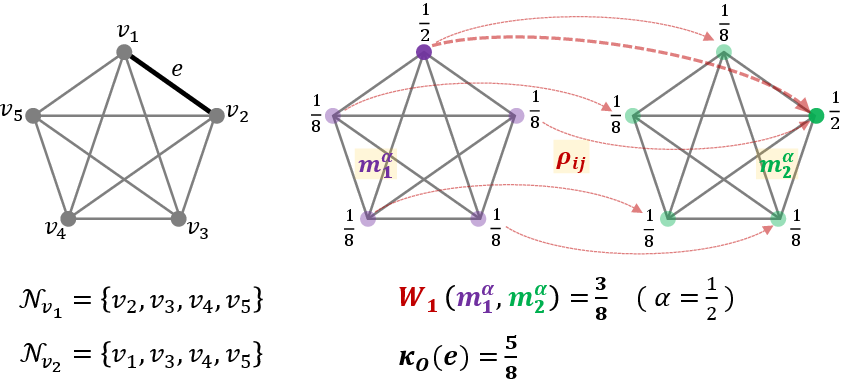
Figure 2: Computation of Ollivier–Ricci curvature for an edge in a complete graph, showing the construction of local probability measures and the optimal transport plan.
Bakry–Émery Curvature: A vertex-based lower bound on Ricci curvature derived from the curvature-dimension inequality, relying on the graph Laplacian and the $\Gamma$ -calculus framework. The curvature at a vertex is determined by the local structure of its punctured 2-ball.
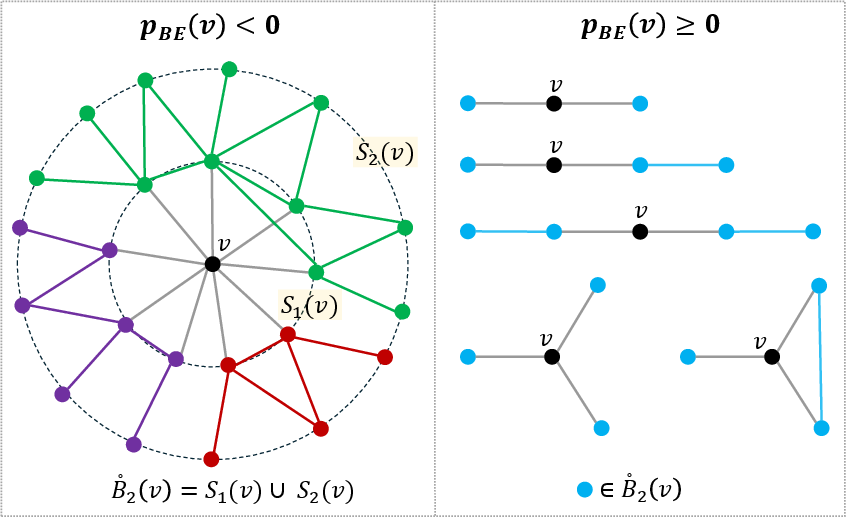
Figure 3: Computation of Bakry–Émery curvature on graphs, highlighting the influence of the local 2-ball structure on the curvature value.
Sectional Curvature: Quantifies the deviation from tripod spaces by measuring the minimal expansion required for three closed balls (centered at three vertices) to intersect. This provides a global geometric invariant for graphs and general metric spaces.
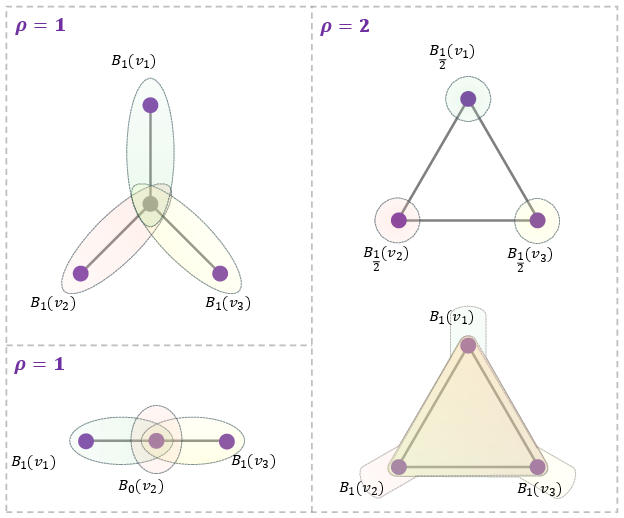
Figure 4: Upper and lower bounds of sectional curvature on graphs, demonstrating the computation on star, path, and complete graph configurations.
Menger-Ricci and Haantjes-Ricci Curvatures: Menger curvature is defined as the reciprocal of the circumradius of a triangle, while Haantjes curvature compares the length of a path to the chord it subtends. Both can be aggregated over edges to yield Ricci-type curvatures.
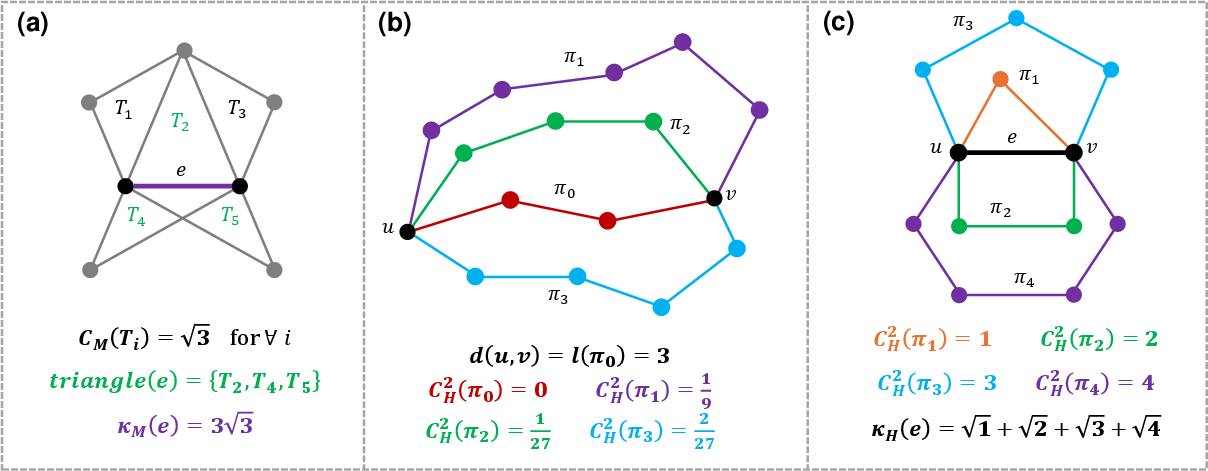
Figure 5: Computation of Menger-Ricci and Haantjes-Ricci curvature on graphs, illustrating aggregation over triangles and paths.
Resistance Curvature: Based on effective resistance in electrical networks, this scalar curvature reflects the structural importance of edges and vertices in maintaining connectivity.
Figure 6: Relationship between random spanning trees, relative resistance of edges, and resistance curvature of vertices.

Computational Pipeline for Curvature-Based Data Analysis

The authors propose a three-step pipeline:

Data Representation: Selection of an appropriate topological model (graph, simplicial complex, cubical complex, hypergraph) based on the data modality.
Curvature Computation: Application of discrete curvature definitions to the chosen representation, with explicit combinatorial or metric formulas for each curvature type.
Feature Extraction: Use of curvature values to featurize vertices, edges, or higher-order structures, enabling multiscale geometric analysis.

The flexibility of Forman-Ricci curvature is emphasized, as it extends naturally to higher-dimensional simplices, allowing for the analysis of higher-order interactions in data.

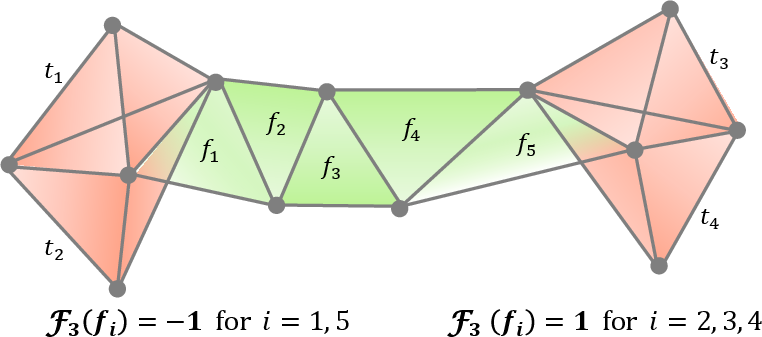
Figure 7: Computation of Forman curvature on 2-simplices in an unweighted simplicial complex, showing the combinatorial dependence on faces, cofaces, and parallel simplices.

Comparative Analysis of Curvature Notions

The review provides a detailed comparison of the qualitative and quantitative behavior of different curvature models on real-world data, such as molecular graphs.

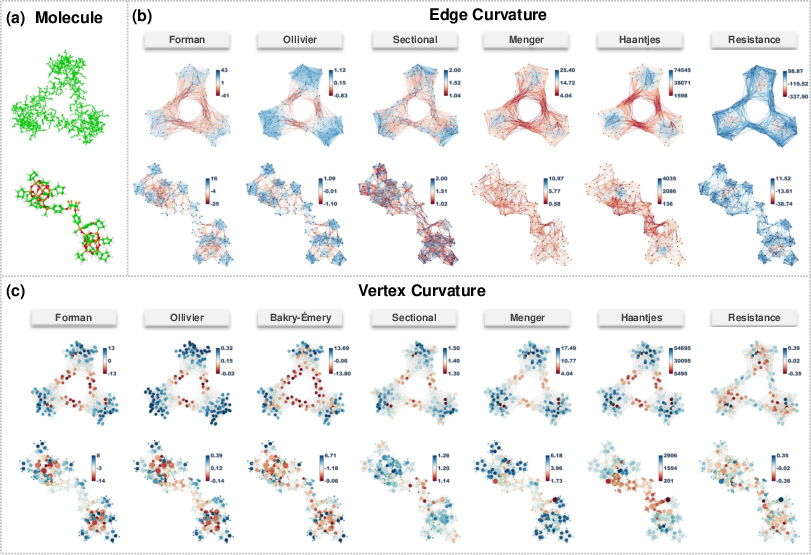
Figure 8: Comparison of different notions of discrete curvature on molecular systems, demonstrating the ability of each curvature to distinguish clusters from bottlenecks.

Key observations include:

Forman-Ricci and Ollivier-Ricci curvatures are sensitive to local bottlenecks and clusters, with negative curvature indicating sparse connectivity.
Sectional curvature provides a global measure, with lower values in tree-like regions and higher values in clique-like regions.
Menger-Ricci and Haantjes-Ricci curvatures, while always non-negative, still differentiate between dense and sparse regions via their aggregation mechanisms.
Resistance curvature captures the importance of edges and vertices in maintaining global connectivity, with high curvature indicating critical points for network robustness.

Applications in Machine Learning

Community Detection

Curvature-based methods for community detection exploit the observation that intra-community edges tend to have positive curvature, while inter-community edges are negatively curved. Two main strategies are:

Incremental Edge Deletion: Iteratively removing negatively curved edges to reveal community structure.
Ricci Flow-Based Methods: Modifying edge weights via discrete Ricci flow, followed by pruning based on curvature-adjusted weights.

These approaches have demonstrated strong empirical performance in both synthetic and real-world networks, with curvature distributions often exhibiting bimodality in networks with pronounced community structure.

Manifold Learning

Curvature-aware manifold learning methods relax the assumption of global or local Euclidean isometry by incorporating curvature information into dimensionality reduction. Both static (curvature-penalized affinity matrices) and dynamic (Ricci flow-based metric learning) approaches are reviewed. Ollivier-Ricci curvature is particularly effective for pruning spurious edges in nearest-neighbor graphs, improving the fidelity of low-dimensional embeddings.

Graph Neural Networks and Representation Learning

Discrete curvature has been integrated into GNNs through several mechanisms:

Graph Rewiring: Removal or reweighting of edges based on curvature to mitigate oversmoothing and oversquashing.
Structural and Positional Encoding: Augmenting node and edge features with curvature-derived statistics to enhance expressivity.
Feature Aggregation: Using curvature to modulate message-passing weights, improving the sensitivity of GNNs to local geometry.
Graph Pooling: Grouping nodes based on curvature similarity to preserve essential structure during pooling operations.
Representation Learning: Embedding graphs in mixed-curvature product manifolds, enabling the modeling of heterogeneous relational structures.

These methods have led to improved performance on tasks such as node classification, link prediction, and graph classification, particularly in settings with complex or hierarchical topologies.

Theoretical and Practical Implications

The survey highlights several theoretical insights:

Discrete curvature provides a principled framework for quantifying geometric and topological properties in non-Euclidean data.
The choice of curvature model should be guided by the data representation, computational constraints, and the specific learning task.
There is substantial complementarity among different curvature notions; combining them can yield richer geometric features.

On the practical side, the review underscores the need for:

Standardized benchmarks for empirical comparison of curvature models.
Scalable algorithms for curvature computation on large and complex data structures.
Extensions of curvature notions to hypergraphs, higher-order complexes, and topological deep learning frameworks.

Future Directions

The authors identify several open challenges:

Development of a unifying theoretical framework to relate and classify discrete curvature models, potentially via semigroup characterizations.
Systematic empirical studies to assess the strengths and limitations of each curvature notion across diverse datasets.
Integration of higher-order curvature models into topological deep learning and geometric machine learning pipelines.
Exploration of curvature-driven learning in domains beyond graphs, such as hypergraphs and simplicial complexes.

Conclusion

This work provides a comprehensive and technically detailed roadmap for curvature-based geometric data analysis and learning. By consolidating mathematical foundations, computational methods, and machine learning applications, it serves as a reference for researchers seeking to leverage discrete curvature in the analysis of complex, non-Euclidean data. The survey demonstrates that discrete curvature is a versatile and interpretable tool, with significant potential for advancing geometric deep learning and topological data analysis.