Tree Training: Accelerating Agentic LLMs Training via Shared Prefix Reuse (2511.00413v1)

Abstract: In agentic LLM scenarios, an agent's interaction process during a single rollout often exhibits branching behaviors. Due to memory retrieval and concurrent tool executions at certain decision points, the token trajectory of one task evolves into a tree-like structure rather than a linear sequence. However, current training pipelines decompose such tree-structured trajectories into separate linear segments, treating each branch as an independent sequence. As a result, shared prefixes across these branches are repeatedly recomputed during both forward and backward passes. To address this inefficiency, we propose Tree Training, a paradigm that computes each shared prefix only once and reuses its intermediate results across related branches during both forward and backward passes, substantially improving computation efficiency in large-scale agentic training. This is achieved via (i) Tree Packing, which efficiently reuses shared computations across trajectories, and (ii) Gradient Restoration, which ensures correct gradient propagation across reused prefixes. Experiments on multiple open-source models demonstrate up to 3.9x reduction in total training time, enabling more efficient agentic LLM SFT and RL training.

• The paper introduces Tree Training, a paradigm that reuses shared token prefixes to eliminate redundant computation, achieving up to 5.7× speedup in ideal settings.
• It employs tree packing strategies, including single-path and multi-path approaches, to optimize memory usage and ensure gradient correctness through a scaling mechanism.
• Experimental results on Qwen3 models demonstrate significant acceleration in both supervised fine-tuning and reinforcement learning, while maintaining numerical fidelity.

Tree Training: Accelerating Agentic LLMs Training via Shared Prefix Reuse

Introduction

The paper introduces Tree Training, a paradigm designed to optimize the training of agentic LLMs by exploiting the inherent tree-structured overlap in token trajectories generated during multi-turn interactions. In agentic scenarios, branching behaviors arise from concurrent tool executions, memory retrieval, and tree-structured planning, resulting in trajectories that share substantial prefix segments. Conventional training pipelines treat each branch as an independent sequence, leading to redundant computation of shared prefixes during both forward and backward passes. Tree Training addresses this inefficiency by computing each shared prefix only once and reusing its intermediate results across all descendant branches, thereby improving computational efficiency in large-scale supervised fine-tuning (SFT) and reinforcement learning (RL) for agentic LLMs.

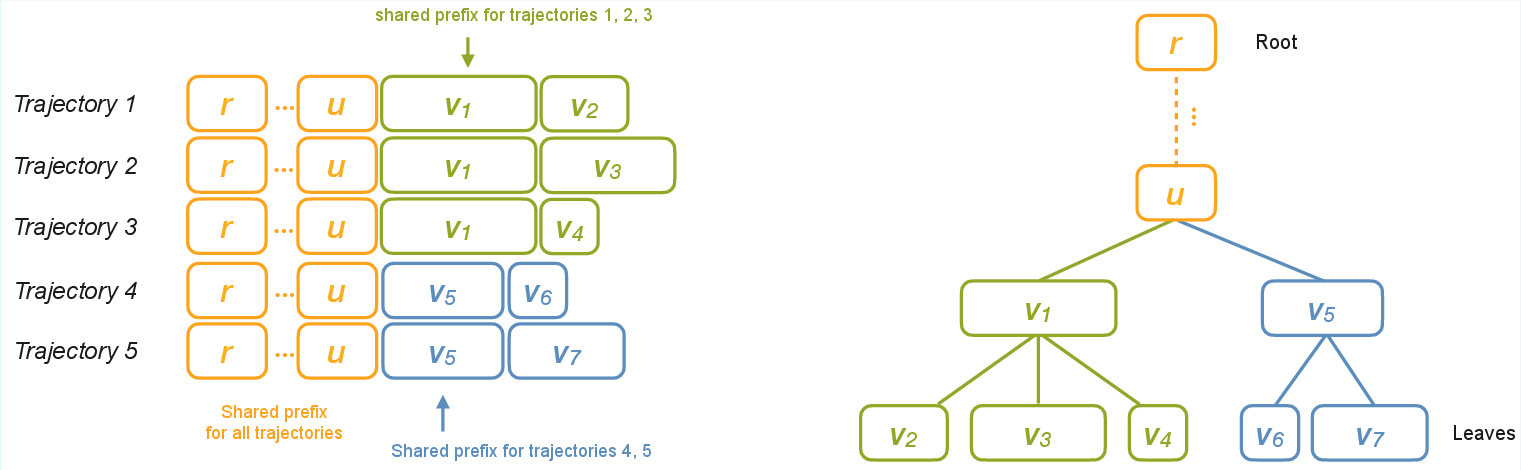
Figure 1: Shared prefixes in agentic trajectories form a hierarchical tree, enabling efficient reuse of computation across branches.

Tree Training Paradigm

Tree Packing

Tree Packing is the core mechanism for representing and processing tree-structured trajectories under memory constraints. It merges overlapping prefixes into a hierarchical tree, where internal nodes represent shared computation and leaves correspond to unique continuations. The packing algorithm optimizes the partitioning of the computation tree into subtrees that fit within a global trajectory-length budget, maximizing reuse of shared prefixes and minimizing overall training cost.

The paper formalizes both single-path and multi-path packing strategies. In single-path packing, a single shared prefix is selected per training step, while multi-path packing generalizes this to allow multiple shared prefixes, further reducing redundant computation. The multi-path dynamic programming formulation is theoretically optimal but computationally expensive; thus, a scalable heuristic is proposed for large trees, prioritizing deep leaves and grouping similar-depth leaves to improve packing homogeneity.

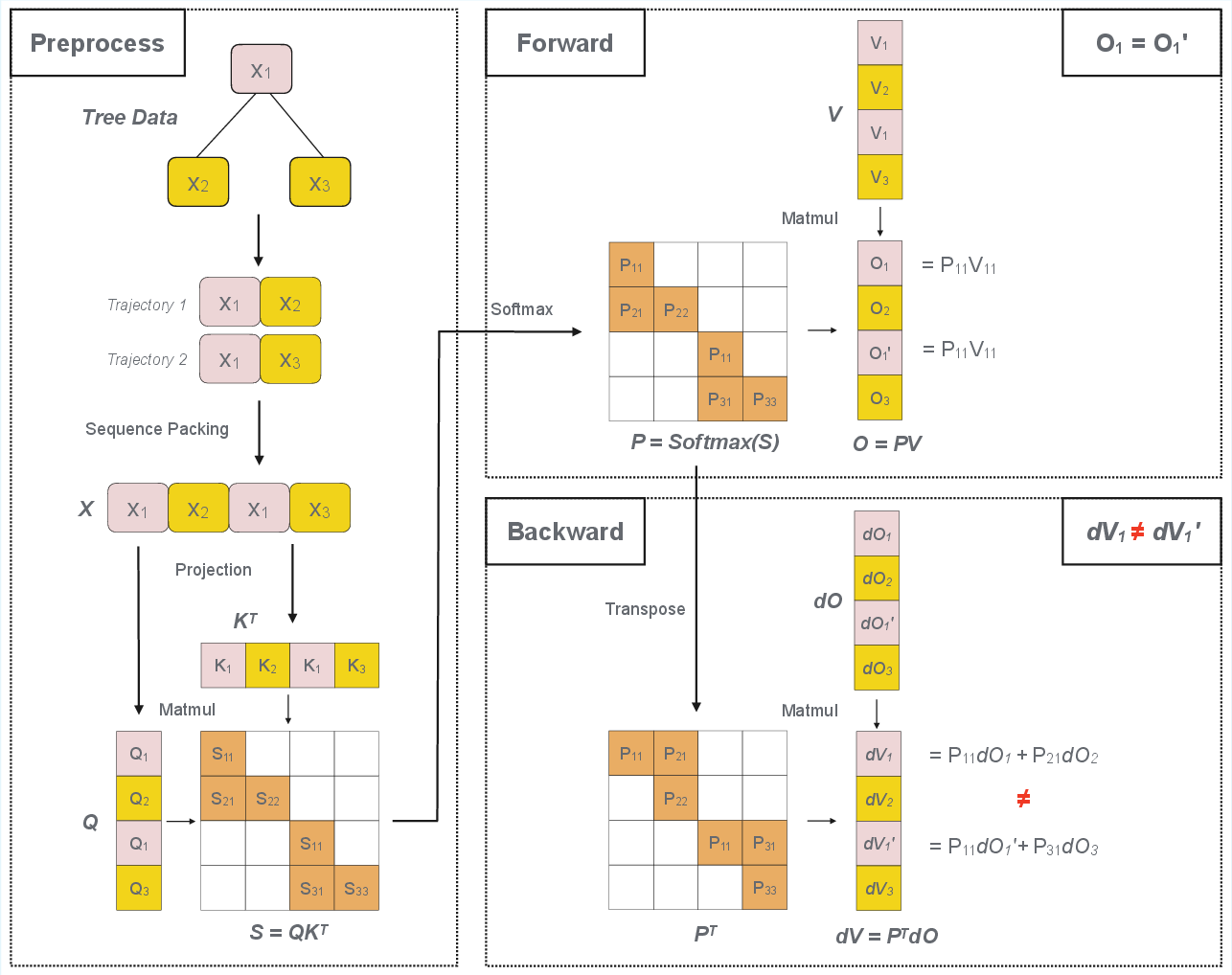
Figure 2: Schematic of preprocess, forward, and backward passes in tree-structured datasets, highlighting prefix and suffix computation.

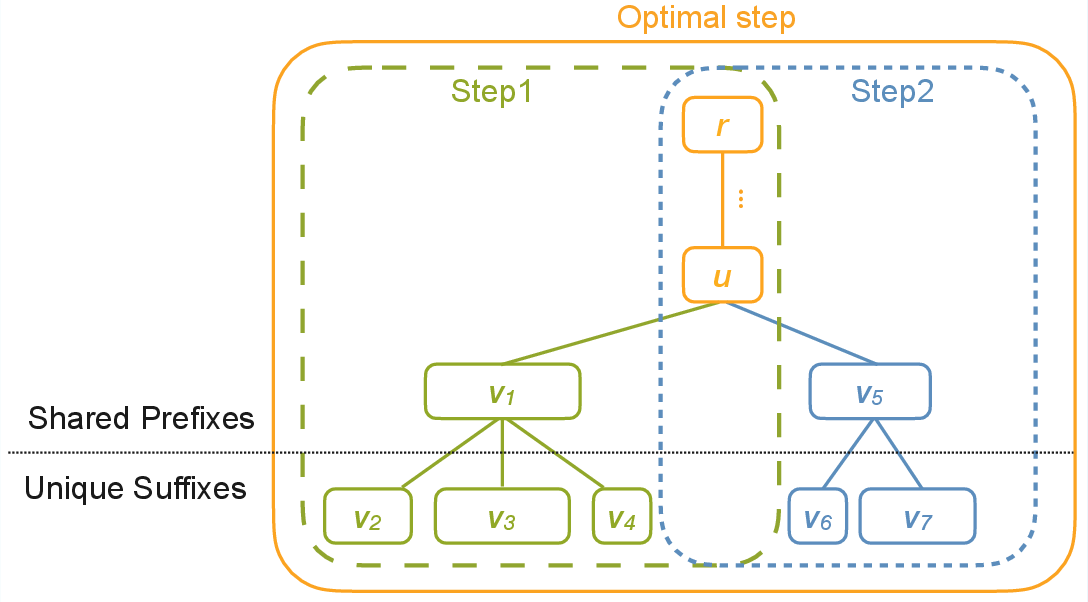
Figure 3: Comparison of single-path and multi-path tree packing, demonstrating superior reuse in the multi-path strategy.

Gradient Restoration

A major technical challenge is ensuring gradient correctness when shared prefixes are computed only once. In the backward pass, gradients for prefix tokens are influenced by all descendant suffixes, making naive reuse of cached activations insufficient. The paper provides a formal analysis of gradient flow in packed prefixes and introduces a gradient restoration algorithm that compensates for omitted redundant computations.

The key insight is that for any linear or attention operation, the gradient for a shared prefix must be scaled by the number of descendant branches that reuse it. This is implemented via a gradient scaler mechanism, which restores the correct influence of each sequence’s prefix on model updates. The approach is transitive across pointwise and attention operations, requiring correction only at the first operation in the backpropagation chain.

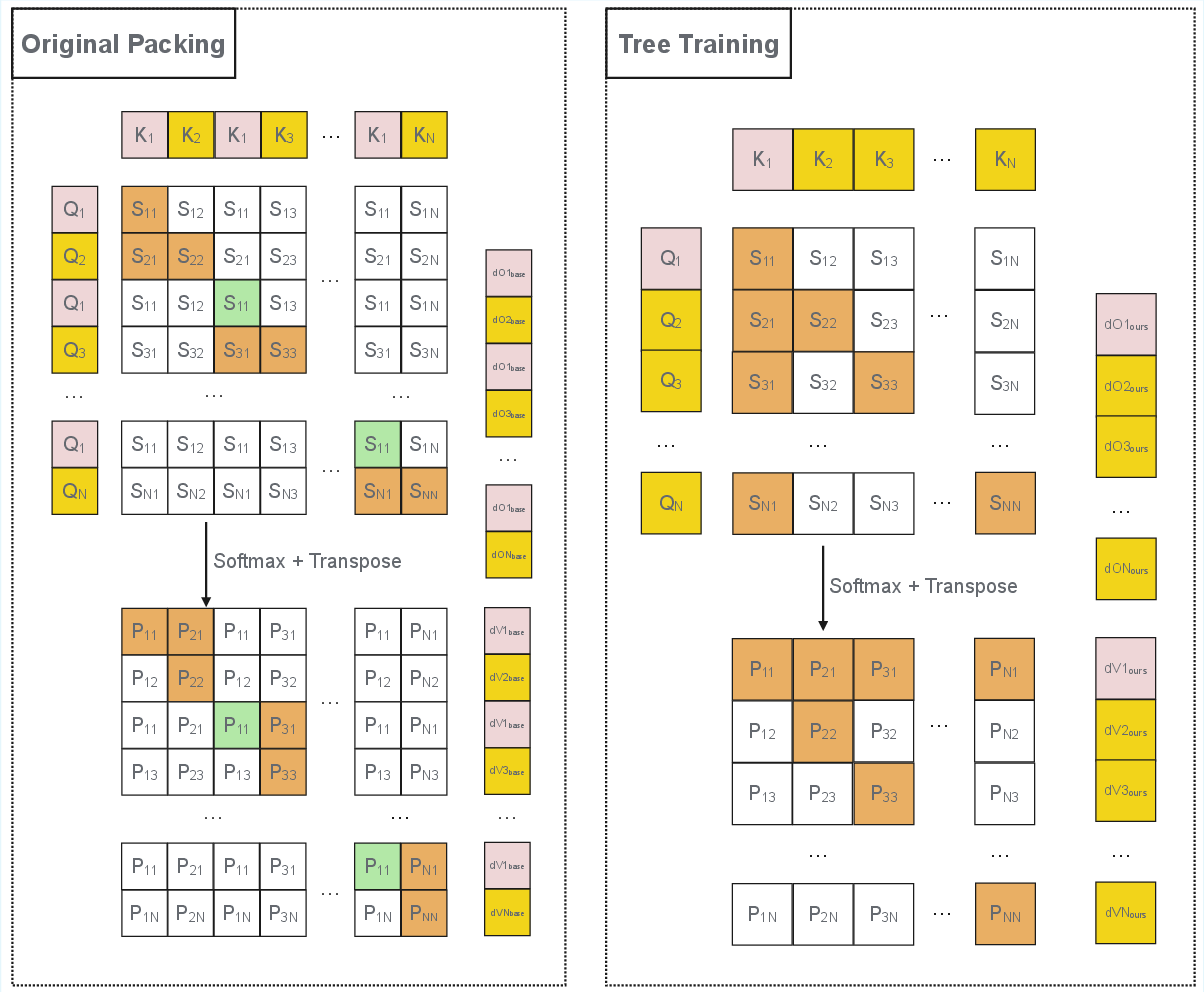
Figure 4: Backward V-gradient computation in tree-packing vs. original packing, with omitted computations highlighted.

Figure 5: Implementation of flattened tree trajectory, including gradient scale tensor, position embedding tensor, and shared-prefix attention mask.

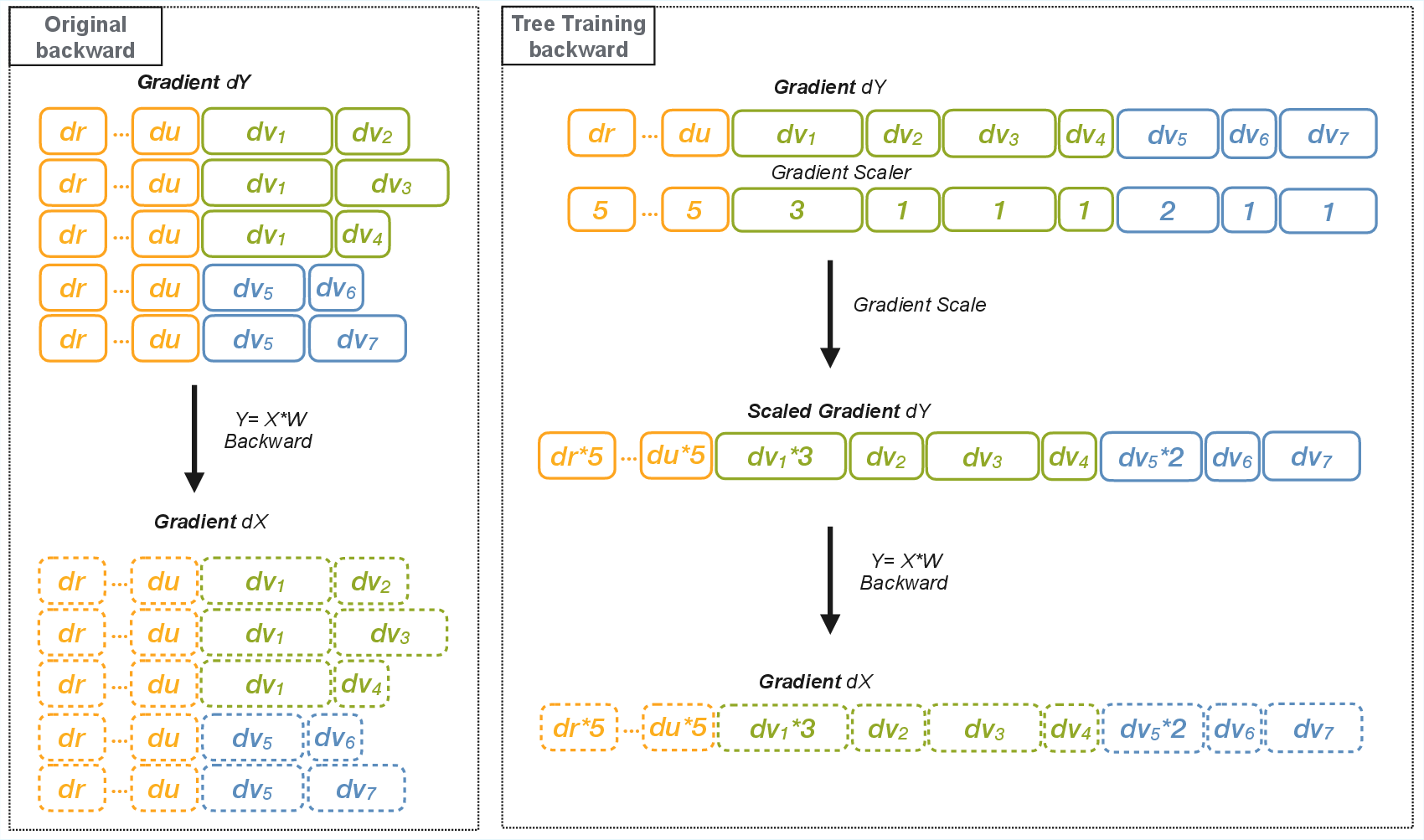
Figure 6: Gradient scaling in Tree Training ensures correct accumulation for shared prefixes reused by multiple trajectories.

Implementation Details

Tree Training is implemented with three main components:

• Shared Prefix Attention Mask: A modified causal mask restricts attention scope, ensuring tokens of different trajectories safely share prefix representations.
• Position Embedding Correction: Position IDs are restored to their original values to maintain consistency in positional information.
• Gradient Scaler: A correction factor is applied during backpropagation to scale gradients of shared prefixes by their reuse counts.

Custom GPU kernels based on Flash Attention V3 are used to efficiently support node-level shared prefix masking.

Experimental Results

Experiments were conducted on Qwen3-8B and Qwen3-32B models using Megatron-LM across synthetic and real-world agentic datasets. The Potential Overlap Ratio (POR) quantifies the intrinsic sub-trajectory overlap, while the Effective Reuse Ratio (ERR) measures realized token reuse under memory constraints.

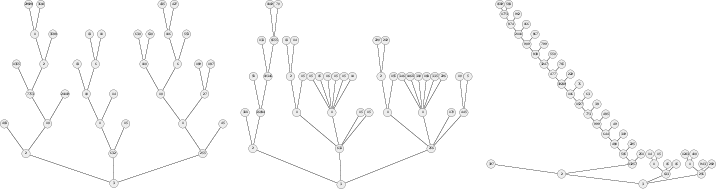
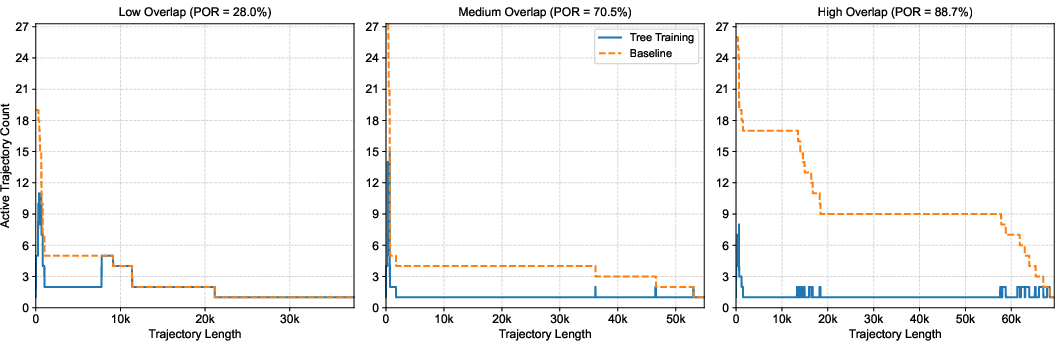
Figure 7: Real agentic trajectory trees with varying degrees of prefix sharing and corresponding token reuse statistics.

Tree Training consistently reduces total training time compared to baseline sequence packing, with improvements scaling monotonically with POR. In ideal settings where full trees fit in memory, up to 5.7× speedup is achieved. Under realistic memory constraints, acceleration remains substantial (4.5–5.3×). On real agentic RL datasets, which exhibit unbalanced and sparse overlap structures, Tree Training achieves up to 3.9× reduction in end-to-end training time. Numerical fidelity is maintained, with loss and gradient deviations within precision tolerance.

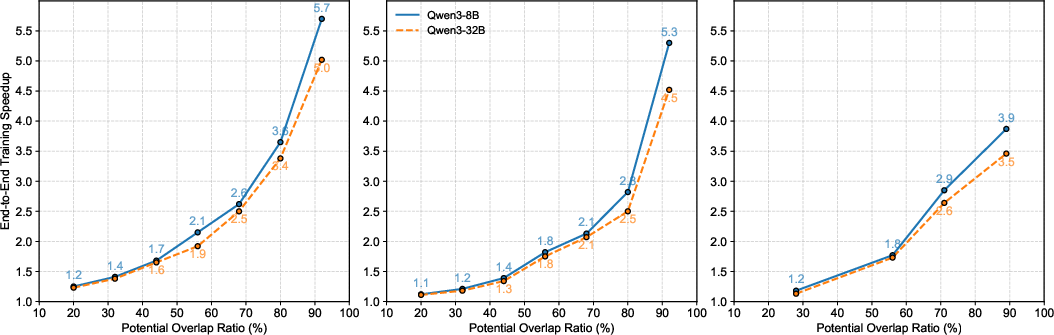
Figure 8: End-to-end training speedup of Tree Training across datasets with varying Potential Overlap Ratios (POR).

Implications and Future Directions

Tree Training demonstrates that exploiting the tree-structured overlap in agentic LLM trajectories yields significant computational savings without compromising training fidelity. The paradigm is broadly applicable to SFT and RL settings, especially in multi-turn, multi-tool, and memory-augmented agentic environments. The approach generalizes to larger models and complex datasets, providing scalable acceleration for agentic LLM training.

Potential future developments include:

• Extending tree packing heuristics for even larger and more irregular trajectory trees.
• Integrating Tree Training with distributed training frameworks to further scale throughput.
• Applying similar computation reuse principles to other model architectures with overlapping computation graphs.
• Investigating the impact of Tree Training on generalization and downstream agentic performance.

Conclusion

Tree Training provides a principled and practical solution for minimizing redundant computation in agentic LLM training by reusing shared prefix activations and gradients. The paradigm achieves substantial end-to-end acceleration, is compatible with standard transformer architectures, and maintains strict gradient correctness. Its applicability to diverse agentic scenarios and scalability to large models position it as a valuable optimization for future LLM training pipelines.