Higher-order phase reduction for delay-coupled oscillators beyond the phase-shift approximation (2510.27524v1)

Abstract: Network interactions between dynamical units are often subject to time delay. We develop a phase reduction method for delay-coupled oscillator networks. The method is based on rewriting the delay-differential equation as an ordinary differential equation coupled with a transport equation, expanding in the coupling strength, and solving the resulting equations order-by-order. This approach yields an approximation of the finite-dimensional phase dynamics to arbitrary order. While in the first-order approximation the time delay acts as a phase shift as expected, the higher-order phase reduction generally displays a less trivial dependence on the delay. In particular, exploiting second-order phase reduction, we prove the existence of a region of bistability in the synchronization dynamics of two delay-coupled Stuart-Landau oscillators.

• The paper introduces a new method that extends phase reduction by accounting for higher-order delay effects beyond simple phase-shift approximations.
• It reformulates delay differential equations into ordinary differential equations with transport equations, revealing complex interactions in delay-coupled systems.
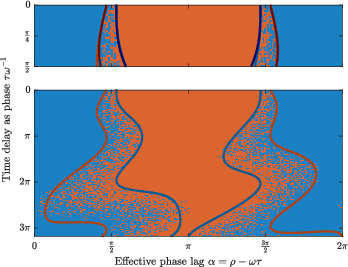
• Application to Stuart–Landau oscillators demonstrates the method’s effectiveness in predicting bifurcation phenomena and bistability in synchronization dynamics.

Higher-order Phase Reduction for Delay-coupled Oscillators

The paper "Higher-order phase reduction for delay-coupled oscillators beyond the phase-shift approximation" (2510.27524) develops an advanced method for phase reduction of networks comprising delay-coupled oscillators. This methodology extends traditional phase reduction approaches by accounting for higher-order effects beyond the simple phase-shift approximation. It achieves this through a novel framework that systematically approximates the finite-dimensional phase dynamics while considering the time delay intricacies. Additionally, the paper presents a second-order phase reduction application, particularly casting light on delay-coupled Stuart–Landau oscillators and their synchronization dynamics.

Phase Reduction Methodology

The proposed methodology reformulates delay differential equations (DDEs) into ordinary differential equations (ODEs) coupled with transport equations, solving them iteratively to approximate phase dynamics to an arbitrary order. While first-order approximations result in a mere phase shift effected by the time delay, higher-order reductions reveal more complex dependencies:

• Phase Shift Approximation: At first order, time delay is represented as a simple phase shift. This common approximation is suitable for initial analyses.
• Complex Delay Effects: The new methodology elucidates intricate dependencies on the delay at higher orders, which can profoundly affect synchronization, stability, and other dynamical properties.

  Figure 1: The bifurcation curves of the one-dimensional phase reduced equations illustrating the transition regions of stability and instability.

The theoretical framework successfully proves, via a constructive theorem, the ability to solve these phase dynamics equations up to any precision in the coupling strength parameter, enhancing the understanding of synchronization phenomena in delayed networks.

Implementation and Applications

The framework's utility is demonstrated by deriving both the first- and second-order phase reduction for delay-coupled Stuart–Landau oscillators. This application underscores its practical relevance:

• Parameters Influence: The resultant phase dynamics reflect complex interactions, revealing parameter regions with bistability, where in-phase and anti-phase synchrony coexist as dynamically stable states.
• Numerical and Analytic Concordance: The presented reduction predicts bifurcation phenomena in numerical simulations of the full DDE system, showcasing its practical fidelity.

This capacity to accurately describe higher-order effects extends the applicability of phase reduction methods to a broader class of systems, especially those where simple phase shift approximations fall short. The rigorously derived analytic expressions offer qualitative insights into phenomena like multistability and synchronization transitions, with direct implications for biological and engineering networks where time delays are intrinsic.

Conclusion

In summary, this research provides a robust extension to phase reduction techniques, capturing higher-order dynamical effects of delays in coupled oscillator networks. By doing so, it fills a significant analytical void, providing tools essential for dissecting complex synchronization phenomena across disciplines. The applications to Stuart–Landau oscillators validate the approach, particularly in contexts where bistability and intricate delay dependencies are pivotal. Future extensions could explore finer aspects of delay interactions and extend the application scope to diverse oscillator network topologies.