AMO-Bench: Large Language Models Still Struggle in High School Math Competitions (2510.26768v1)
Abstract: We present AMO-Bench, an Advanced Mathematical reasoning benchmark with Olympiad level or even higher difficulty, comprising 50 human-crafted problems. Existing benchmarks have widely leveraged high school math competitions for evaluating mathematical reasoning capabilities of LLMs. However, many existing math competitions are becoming less effective for assessing top-tier LLMs due to performance saturation (e.g., AIME24/25). To address this, AMO-Bench introduces more rigorous challenges by ensuring all 50 problems are (1) cross-validated by experts to meet at least the International Mathematical Olympiad (IMO) difficulty standards, and (2) entirely original problems to prevent potential performance leakages from data memorization. Moreover, each problem in AMO-Bench requires only a final answer rather than a proof, enabling automatic and robust grading for evaluation. Experimental results across 26 LLMs on AMO-Bench show that even the best-performing model achieves only 52.4% accuracy on AMO-Bench, with most LLMs scoring below 40%. Beyond these poor performances, our further analysis reveals a promising scaling trend with increasing test-time compute on AMO-Bench. These results highlight the significant room for improving the mathematical reasoning in current LLMs. We release AMO-Bench to facilitate further research into advancing the reasoning abilities of LLMs. https://amo-bench.github.io/
Summary
- The paper introduces AMO-Bench, a novel evaluation benchmark with 50 original IMO-level math problems that assess LLM mathematical reasoning using rigorous grading protocols.
- The evaluation reveals that state-of-the-art LLMs achieve only 52.4% accuracy, underscoring significant performance gaps despite emerging latent capabilities.
- Longer model outputs correlate with improved accuracy, indicating that enhanced context lengths and advanced sampling strategies are needed for better reasoning.
AMO-Bench: Evaluating LLMs on Olympiad-Level Mathematical Reasoning
Benchmark Motivation and Design
AMO-Bench is introduced as a rigorous evaluation suite for mathematical reasoning in LLMs, specifically targeting the limitations of existing benchmarks derived from high school math competitions. The saturation of performance on datasets such as AIME24/25, where top-tier models routinely exceed 90% accuracy, necessitates a more challenging and uncontaminated benchmark. AMO-Bench comprises 50 entirely original problems, each cross-validated by multiple experts to meet or exceed the difficulty of the International Mathematical Olympiad (IMO). The benchmark is designed to avoid data leakage and memorization, with a multi-stage pipeline for problem creation, quality assurance, originality verification, and difficulty filtering.
Figure 1: The construction and grading pipeline of AMO-Bench.
Problems are categorized into algebraic equations/inequalities, functions/sequences, geometry, number theory, and combinatorics, reflecting the breadth of MO-level content.
Figure 2: Distribution of problem categories.
Each problem requires only a final answer, enabling automated grading via parser-based or LLM-based methods depending on answer type. Human-annotated reasoning paths are provided for transparency and further research utility.
Grading Methodology and Dataset Properties
AMO-Bench employs a hybrid grading strategy. Parser-based grading is used for numerical, set, and variable-expression answers, leveraging strict equivalence checks and value substitution for expressions. Descriptive answers are graded using an LLM (o4-mini), with majority voting across multiple samples to ensure robustness. Manual validation of 1,000 responses yielded a grading accuracy of 99.2%, supporting the reliability of the evaluation protocol.
The benchmark's annotated solutions are significantly longer than those in AIME24 and MATH500, indicating higher reasoning complexity and token requirements.
Experimental Results: LLM Performance Analysis
A comprehensive evaluation of 26 LLMs, spanning both proprietary and open-source models, reveals substantial deficiencies in advanced mathematical reasoning. The highest accuracy on AMO-Bench is 52.4% (GPT-5-Thinking High), with most models below 40%. This is in stark contrast to performance on saturated benchmarks.
Figure 3: Performance of top-tier reasoning models on AMO-Bench and existing math benchmarks.
The evaluation protocol samples each model 32 times per problem (AVG@32), ensuring stability in reported metrics.
Figure 4: The AVG@32 performance of various LLMs on AMO-Bench.
Notably, open-source models are closing the gap with proprietary systems, with the best open-source model trailing the top result by only 5%. Some non-reasoning models (e.g., Qwen3-Max-Instruct, LongCat-Flash) outperform several reasoning-specialized models, indicating that architectural advances and scaling can yield emergent reasoning capabilities.
Reasoning Efficiency and Scaling Trends
A key finding is the correlation between model output length and accuracy: higher-performing models generate substantially longer outputs, often exceeding 35K tokens per completion. This trend is consistent across both reasoning and non-reasoning models.
Figure 5: The AVG@32 performance of LLMs vs. the average model output length.
Benchmarks with higher difficulty (lower accuracy) induce longer model outputs, suggesting that output length is a proxy for reasoning challenge.
Figure 6: The relationship between accuracy and average output length on different math benchmarks.
Test-time scaling—allocating more compute and allowing longer outputs—continues to yield near-linear improvements in accuracy with respect to the logarithm of output length, even on AMO-Bench.
Figure 7: The model performance and output length under different reasoning effort settings.
This scaling law is consistent with prior observations on other math benchmarks, indicating that current LLMs have not saturated their reasoning capacity on AMO-Bench.
Pass@ Metrics and Model Potential
Analysis of pass@ metrics demonstrates that top-tier models achieve over 70% pass@32, indicating latent potential for further improvement via reinforcement learning or enhanced sampling strategies.
Figure 8: The pass@ trend of various LLMs with increasing .
This suggests that while models often fail to consistently identify the correct reasoning path, they possess the underlying capability to solve these problems given sufficient sampling or optimization.
Implications and Future Directions
AMO-Bench exposes the substantial gap between current LLM mathematical reasoning and the requirements of Olympiad-level problem solving. The benchmark's design—originality, difficulty, and robust grading—mitigates contamination and enables reliable longitudinal tracking of model progress. The observed scaling trends imply that further increases in model size, context length, and inference budget will continue to drive improvements, but architectural and training innovations are required to close the gap with human experts.
The inclusion of human-annotated reasoning paths opens avenues for research in prompt engineering, error analysis, and interpretability. The benchmark also provides a foundation for reinforcement learning from human feedback (RLHF) and other optimization strategies targeting mathematical reasoning.
Conclusion
AMO-Bench establishes a new standard for evaluating advanced mathematical reasoning in LLMs, with 50 original, IMO-level problems and a robust automated grading protocol. Experimental results demonstrate that state-of-the-art models still struggle, achieving only moderate accuracy and requiring extensive output lengths. The benchmark highlights both the limitations and the scaling potential of current LLMs, providing a critical resource for future research in mathematical reasoning and model development.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
Overview
This paper introduces AMO-Bench, a new and very challenging math test designed to check how well advanced AI models can reason through hard problems. The authors noticed that many popular high school math competition benchmarks (like AIME) have become too easy for top AI models and may include questions the models have already seen. So they built a tougher, cleaner test: 50 original, Olympiad-level problems that expect only a final answer, making grading automatic and fair.
Key Questions
The paper asks:
- Can we create a truly challenging, fair math benchmark that today’s top AI models can’t easily “ace”?
- How do current AI models perform on harder, Olympiad-level problems they haven’t seen before?
- Does giving AI more “thinking time” (longer answers) help them solve tougher problems?
- What signals tell us a benchmark is actually hard?
How Did They Build and Test It?
Building the benchmark
Think of AMO-Bench like a brand-new championship exam for AI:
- Human math experts wrote 50 original problems covering topics like algebra, functions and sequences, geometry, number theory, and combinatorics.
- Each problem was reviewed by multiple experts to ensure it’s clear, correct, and at least as hard as International Mathematical Olympiad (IMO) standards.
- They checked online and against past datasets to avoid repeats or very similar questions. This helps prevent “memorization.”
- Experts also wrote detailed solution steps to show how to solve each problem and support later analysis.
Grading answers
To keep grading fast and fair:
- Every problem asks for a single final answer (not a full proof), like a number, set, or formula.
- Simple answers (like a number or set) are graded automatically by a computer “parser” that checks if the AI’s answer matches the correct one.
- More complex answers (short explanations with cases) are judged by a separate AI “grader” that acts like a teacher, using multiple checks to be consistent.
Testing AI models
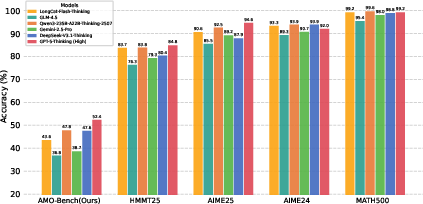
To see how well different AI models do:
- They tested 26 models (both commercial and open-source).
- Each model answered each problem 32 times; they reported the average score (called AVG@32) to get stable results.
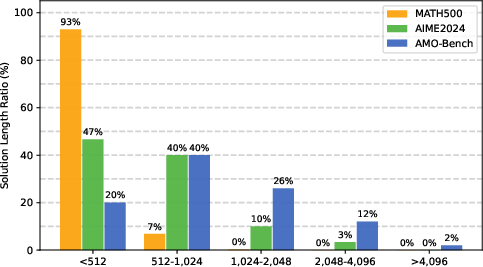
- They also tracked how long the answers were. In AI, “tokens” are like pieces of words—the more tokens used, the more the AI is “thinking.”
Main Results
Here’s what they found:
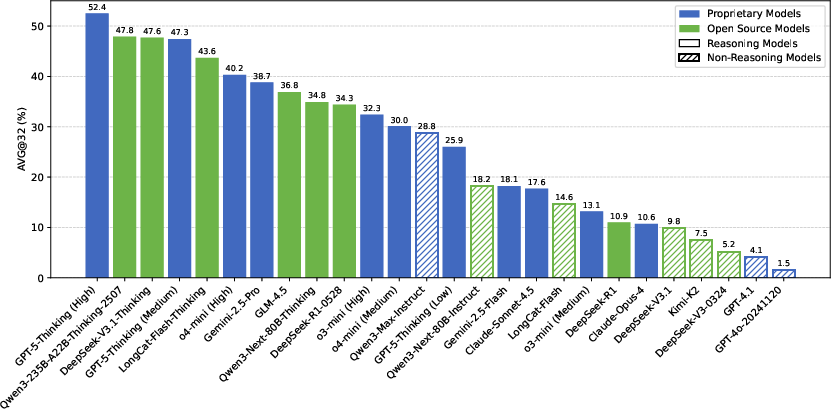
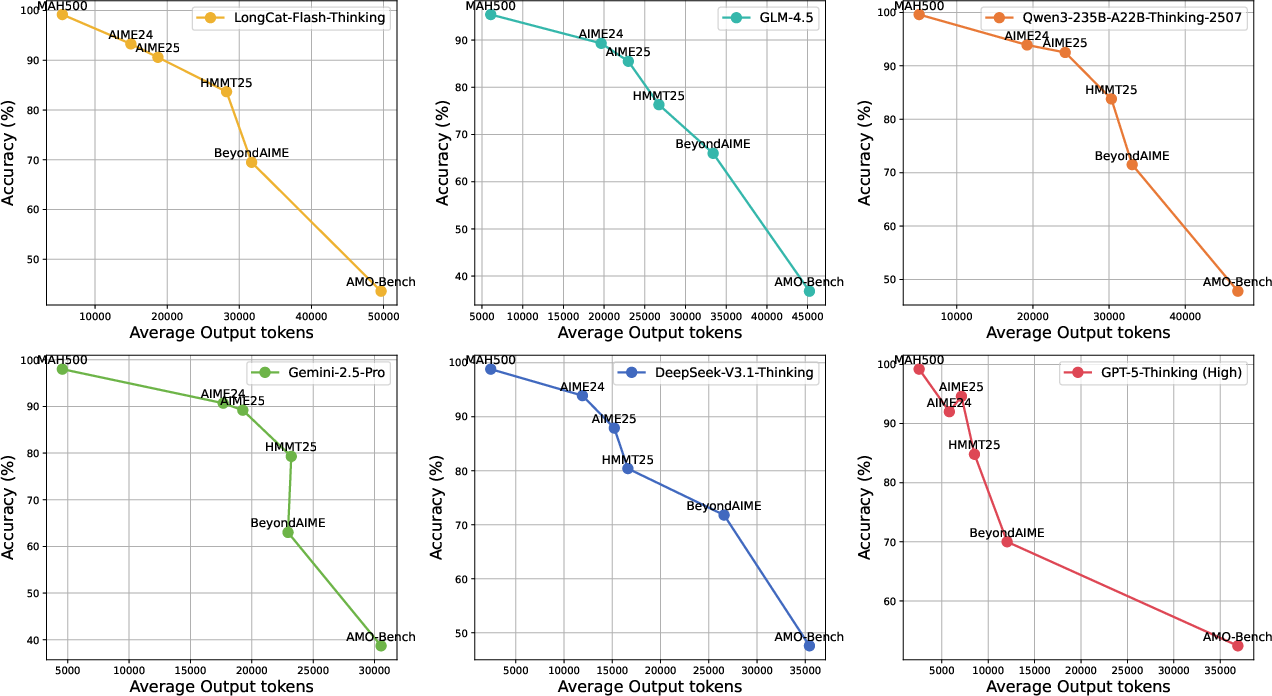
- Even the best model only scored 52.4% on AMO-Bench. Most models scored under 40%. This shows the benchmark is genuinely hard.
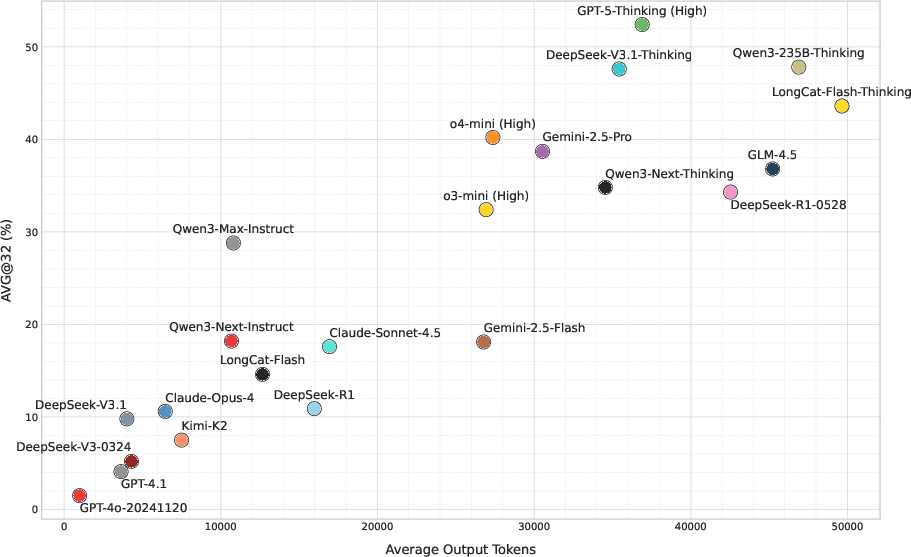
- Models used far more tokens (much longer answers) on AMO-Bench than on easier benchmarks like AIME. Longer answers suggest more reasoning effort.
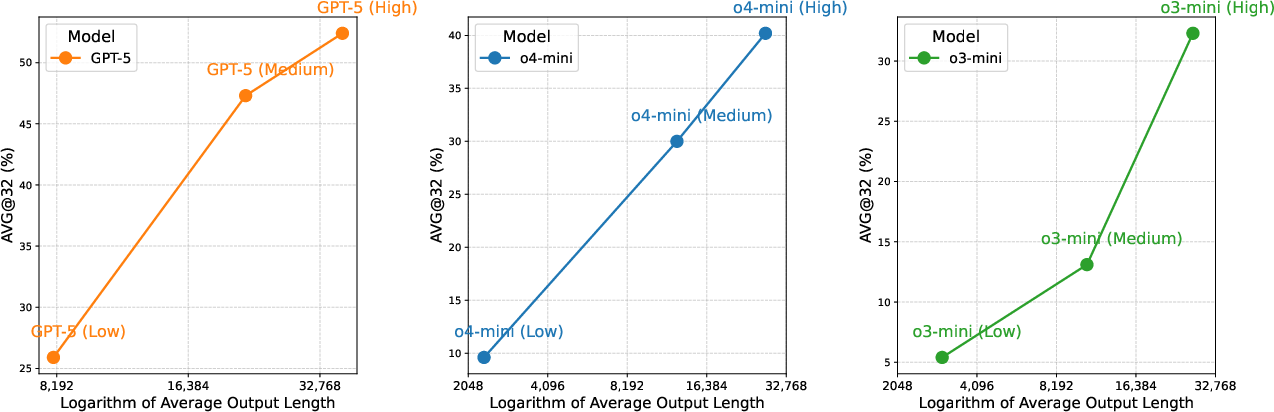
- Performance generally increases as models “think” more: if you let a model generate longer answers, its accuracy grows in a steady way.
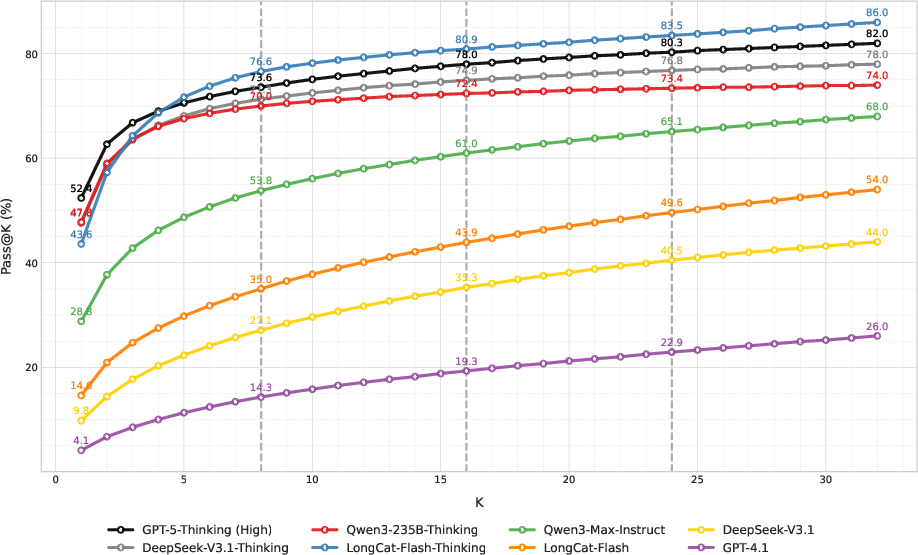
- Top models have high “pass@32” scores (over 70%). “pass@k” means, “If the model tries k different solution attempts, how often does at least one get it right?” High pass@32 suggests the model often gets close and sometimes finds the correct path—it just isn’t consistent yet.
- Some non-specialized models (“non-reasoning” models) performed better than expected, showing that strong general models can tackle complex math reasoning too.
Why is this important?
- It proves that current AI still struggles with truly hard math reasoning, even if they do well on popular contests.
- It provides a reliable, modern test that can track future improvements without being biased by old, possibly memorized questions.
- It shows that test-time scaling (letting models think longer) can help, which guides how to evaluate and improve models.
Why This Matters
AMO-Bench gives researchers a clean, tough challenge to measure progress in genuine reasoning, not just pattern matching. Because all problems are original and final-answer-based:
- It reduces the chance of “cheating” through memorization.
- It makes grading fast, consistent, and reproducible.
- It pushes AI to improve on the kind of deep thinking required in Olympiad-level math.
The benchmark also reveals useful signals:
- Longer outputs are a sign a benchmark is harder because the model needs more steps to reason.
- Allowing more attempts or more “thinking time” improves results, which helps plan better evaluations and training.
What Could Happen Next
- Researchers can use AMO-Bench to build better reasoning strategies and training methods for AI.
- Future AI models might learn to be more consistent, turning those high pass@32 potentials into higher one-shot accuracy.
- The community can track progress on a public leaderboard and develop new tools to handle tough problems more reliably.
- Over time, improvements on AMO-Bench may transfer to real-world tasks that need careful, multi-step thinking.
In short, AMO-Bench is like a new, super-challenging math tournament for AI. It shows that even the best models still have room to grow—and gives a fair, practical way to measure how they improve.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a single, actionable list of what remains uncertain or unexplored in the paper and benchmark, prioritized to guide follow-up work.
- Dataset scale and balance: Only 50 problems (with just 5 in geometry) limit statistical power and topic coverage; expand the set and balance category representation to reduce variance and enable reliable per-area comparisons.
- Difficulty calibration: “IMO-level or higher” is judged by experts without reporting inter-rater reliability, rubrics, or quantitative calibration (e.g., human solve rates, time-to-solve, item-response-theory parameters); establish and release such calibration to make difficulty claims auditable.
- Human baselines: No controlled human benchmarks (e.g., top contestants vs. average trained students) are provided; collect and report human accuracy and time to anchor model performance.
- Originality assurance: 10-gram matching and web search can miss paraphrased or structurally similar problems; add semantic/embedding-based near-duplicate detection, solver-canonicalization checks, and third-party audits to strengthen contamination safeguards.
- Post-release contamination: No plan for hidden test sets, rolling refresh, or sequestered evaluation to prevent training-on-test after release; define a maintenance protocol and decontamination strategy.
- Selection bias in difficulty filtering: Pre-filtering with specific advanced models (3 samples, “fail by ≥2 models”) can embed model-specific blind spots; validate with a broader, disjoint set of models and/or human solvers and quantify selection bias.
- Final-answer-only limitation: The benchmark does not evaluate reasoning faithfulness, step validity, or partial credit; incorporate protocol(s) that assess alignment with human-annotated reasoning paths and measure step-level correctness and minimality.
- Untapped human solutions: Human-written reasoning paths are not used in evaluation; create metrics that compare model chains-of-thought to human paths (e.g., overlap, step correctness, plan adherence).
- Grading robustness (LLM-based): The descriptive-answer grader uses a single proprietary model (o4-mini, Low) with majority vote; cross-validate with multiple independent graders, report inter-grader agreement, release seeds, and probe susceptibility to prompt injection or adversarial formatting.
- Parser/equivalence gaps: Random pointwise checks for variable expressions can misjudge identity (especially piecewise/domain constraints); specify the number and range of test points and add CAS-based symbolic equivalence checks to reduce false positives/negatives.
- Numeric tolerance policy: The “≥4 decimal places” rule may penalize valid exact forms or tighter approximations; clarify equivalence rules across exact/approximate forms and define tolerance by problem specification.
- Set/tuple normalization: Rules for ordering, duplicates, and canonical formatting in set/tuple answers are not fully specified; formalize normalization and edge-case handling to avoid grader brittleness.
- Grading auditability: The reported 99.2% grading accuracy on 1,000 responses lacks stratification (by answer type/problem) and released test artifacts; publish the audit set, per-type confusion, and known failure modes.
- Metric definition clarity: AVG@32 is not formally defined (average of accuracies across 32 samples vs. pass@32); standardize metrics, report pass@1, pass@k with confidence intervals, and provide per-problem variance to support significance testing.
- Compute fairness: Models are evaluated with their maximum allowed context/output lengths, yielding unequal compute budgets; provide compute-normalized leaderboards (e.g., fixed output-token caps) and report accuracy-vs-compute frontiers.
- Sampling protocol sensitivity: Temperatures differ across model classes (1.0 vs. 0.7), potentially biasing results; include ablations over temperature/top-p, share seeds, and assess sensitivity to decoding choices.
- Scaling law generality: The near-linear accuracy vs. log-output-length trend is shown for few models and a limited length range; test more models, broader compute regimes, and identify diminishing returns or optimal compute allocation strategies.
- Prompt sensitivity: Only a single prompt template is used; run prompt ablations (formatting, instruction strength, exemplar use) and quantify model ranking stability under prompt changes.
- Environment controls: The closed-book assumption and tool/internet access controls are not specified; formalize evaluation conditions (offline mode, tool bans/allowances) and add a tool-augmented track (e.g., CAS, solvers) for agents.
- Modality and language scope: Tasks are text-only and English-only; add bilingual/multilingual variants and geometry items with diagrams to assess multi-modal and cross-lingual reasoning.
- Error taxonomy: No systematic analysis of failure modes (by topic, technique, step type, or trap patterns); release per-problem skill tags and conduct error taxonomies to enable diagnostic evaluation and targeted training.
- Per-category difficulty: Performance is not broken down by category or technique; report category-level accuracy and time/length to reveal domain-specific weaknesses.
- Leaderboard stability: With N=50, model rankings can be volatile; publish bootstrap confidence intervals, per-problem scores, and guidance on minimal sample sizes for stable comparisons.
- Reproducibility of post-processing: Custom parsing/post-processing tweaks are mentioned but not fully documented; release deterministic parsers, normalization rules, and unit tests to ensure replicability.
- Adversarial robustness: No tests for adversarial inputs designed to fool the parser or LLM grader; incorporate adversarial suites and hardening measures (e.g., input sanitization, constrained parsing).
- Sustainability/cost: Very long outputs (35K+ tokens) inflate evaluation cost; define standardized low-, medium-, and high-budget settings and report cost-normalized performance.
- Governance and versioning: Long-term update cadence, governance (who approves new items), and versioning policy are unspecified; formalize governance and changelogs to maintain benchmark integrity.
- External validity: Problems may reflect particular stylistic/region-specific contest traditions; validate on newly released, independent competitions to test generalization and avoid style overfitting.
- Use of verifiers/process rewards: The benchmark does not evaluate verifier-augmented methods or process-supervised models; add tracks that allow verifiers, step scoring, and self-consistency reranking to paper method-level advances.
Practical Applications
Immediate Applications
The following applications can be deployed now based on AMO-Bench’s released dataset, code, grading pipeline, and empirical findings on test-time scaling and pass@k behavior.
- AI model evaluation and selection for reasoning-critical tasks [AI/ML, Software]
- Use AMO-Bench and AMO-Bench-P to screen and rank LLMs for complex mathematical reasoning workloads, reporting AVG@32, pass@k, and output-length metrics to assess cost-performance trade-offs.
- Workflow: integrate the public evaluation harness and leaderboard; run 32-sample evaluations; track accuracy vs. average completion tokens; produce capability scorecards for procurement or internal model governance.
- Assumptions/dependencies: access to models with sufficient context/output limits; compute budget for up to ~35K completion tokens; acceptance of final-answer grading as a proxy for reasoning quality; dataset licensing and compliance.
- EdTech auto-grading and contest preparation tools [Education]
- Deploy parser-based grading for numeric/set/variable-expression answers (39/50 problems) and an LLM-based majority-vote grader for descriptive answers, with precision constraints (≥4 decimal places) and standardized LaTeX “\boxed{}” output.
- Products/tools: “AMO-Grader API” for LMSs and Olympiad prep platforms; teacher dashboards showing solution correctness and human-annotated reasoning paths; adaptive practice using AMO-Bench-P for faster feedback.
- Assumptions/dependencies: reliable LaTeX parsing via math-verify; availability of a grading LLM (e.g., o4-mini) for descriptive items; 99.2% grading accuracy validated on 1,000 samples but still requires spot checks; platform support for LaTeX formatting.
- Research baselines and reproducible evaluation for mathematical reasoning [Academia]
- Employ AMO-Bench’s original, IMO-level problems and uncontaminated pipeline (expert cross-check + 10-gram + web search) to paper generalization, contamination control, and scaling laws of reasoning (near-linear performance growth vs. log output length).
- Workflow: use the released prompts and sampling protocol (temperature, top-k/p, AVG@32); analyze pass@k curves as improvement potential signals; compare reasoning vs. non-reasoning models under the same token budget.
- Assumptions/dependencies: consistent sampling settings; transparent reporting (tokens, pass@k); compute availability for multi-sample runs; acceptance of final-answer tasks as a high-quality proxy for reasoning difficulty.
- Test-time compute budgeting and product cost planning [Software, Finance/Operations]
- Apply the observed near-linear accuracy gain vs. log completion length to define inference budgets (e.g., stepwise increases in output tokens until diminishing returns) for reasoning features in commercial products.
- Tools/workflows: “Compute Budget Planner” that maps target accuracy to token budgets and costs; dynamic test-time scaling toggles in production; A/B tests measuring ROI of longer reasoning chains.
- Assumptions/dependencies: accurate token accounting; cost models per 1K tokens; tolerance for latency; user-experience impact of longer completions.
- Dataset governance and anti-contamination checks [AI/ML, Policy]
- Adopt AMO-Bench’s originality workflow (multi-expert blind review + 10-gram matching + web search) to audit internal benchmarks and training corpora for leakage and duplication.
- Tools: “Benchmark Contamination Checker” that can be repurposed for other domains (e.g., coding, physics).
- Assumptions/dependencies: stable web search interfaces; curated reference corpora for n-gram comparison; expert availability for blind reviews.
- Prompt and output-standardization for automated verification [Software, Education]
- Use AMO-Bench’s prompt templates (final-answer prefix + LaTeX \boxed{} + precision rules) to make model outputs parser-friendly and verifiable at scale.
- Products: SDKs for “answer-format enforcement” in math tutoring apps; CI checks for math agents generating numerical or set outputs.
- Assumptions/dependencies: adherence to output-format constraints by models; robust post-processing to handle edge cases (e.g., equivalence checks for variable expressions).
- Risk communication for high-stakes quantitative tasks [Policy, Finance, Engineering]
- Communicate current limitations: even top models cap around ~52% accuracy on AMO-Bench and often require very long outputs; caution against unsupervised use in financial modeling, safety-critical engineering, or regulatory compliance calculations.
- Workflow: build internal risk memos and guidelines referencing AMO-Bench results; require human oversight for complex math tasks.
- Assumptions/dependencies: organizational buy-in; alignment with responsible AI frameworks; acceptance of benchmark relevance to intended tasks.
- Student self-assessment and coach-led training [Daily Life, Education]
- Learners use AMO-Bench problems and human-annotated solutions to diagnose strengths/weaknesses; clubs and coaches deploy auto-grading to run practice contests and track progress.
- Tools: practice sets with immediate feedback; difficulty-aware scheduling (AMO-Bench-P for quick sessions; full AMO-Bench for deeper sessions).
- Assumptions/dependencies: familiarity with LaTeX inputs/outputs; access to grading API; careful interpretation of LLM-generated hints vs. official solutions.
Long-Term Applications
These applications require further research, scaling, workflow development, or broader ecosystem adoption.
- Proof-based auto-grading and robust mathematical verifiers [Education, Academia, AI/ML]
- Extend beyond final-answer evaluation to automated proof checking with formal verifiers or improved LLM grading agents; support IMO/USAMO-style proofs with reliability comparable to human judges.
- Products: “Proof Grader” with majority voting, verifier ensembles, and formal methods integration (proof assistants).
- Assumptions/dependencies: advances in verifier reliability; high-quality structured proof representations; benchmark expansions with proof annotations.
- RL training pipelines guided by pass@k and difficulty calibration [AI/ML]
- Use AMO-Bench pass@k curves to shape reinforcement learning curricula (curriculum pace, sampling strategies, self-play with verifiers) and improve “reasoning robustness” on hard problems.
- Tools: reward-modeling on equivalence checks; difficulty-aware sampling; self-consistency with efficient test-time scaling.
- Assumptions/dependencies: availability of large-scale training compute; stable reward signals; careful avoidance of overfitting to benchmark specifics.
- Sector-specific reasoning agents for quantitative decision-making [Finance, Engineering, Energy, Healthcare]
- Develop specialized math agents that combine test-time scaling, multi-sample aggregation (pass@k-style), and domain-specific verification for tasks like portfolio risk, grid optimization, treatment dose calculations, or structural analysis.
- Products: “Quant Reasoning Copilot,” “Operations Research Assistant,” “Clinical Dosing Calculator” powered by verifier-backed reasoning.
- Assumptions/dependencies: domain datasets with verifiable ground truths; strict validation and regulatory compliance; integrated human-in-the-loop safeguards.
- Standardized capability certifications and procurement thresholds [Policy, Government, Enterprise]
- Codify minimum performance and reliability thresholds (e.g., AVG@32 ≥ X on AMO-Bench-P; pass@32 ≥ Y; max token cost ≤ Z) for public-sector or enterprise adoption of reasoning models.
- Tools: “Reasoning Readiness Scorecards” included in RFPs; independent third-party audits referencing AMO-Bench or successor benchmarks.
- Assumptions/dependencies: consensus on relevant metrics and tasks; periodic updates to avoid saturation; governance bodies to maintain standards.
- Cross-domain benchmark construction using AMO-Bench’s pipeline [Academia, AI/ML]
- Replicate the originality/difficulty review and mixed grading approach to build high-difficulty, low-contamination benchmarks for physics, computer science proofs, and applied math (e.g., HARDMath2-like domains).
- Products: “FrontierBench Builder” toolkit for multi-subject reasoning evaluation.
- Assumptions/dependencies: expert author/reviewer pools; scalable grading methods; domain-appropriate verifiers.
- Difficulty-aware adaptive tutoring and curriculum sequencing [Education]
- Use model output-length as a difficulty proxy to calibrate learner progression, dynamically allocate hints, or trigger escalations to human tutors when token budgets exceed thresholds without accuracy gains.
- Products: “Adaptive Reasoning Tutor” that modulates chain-of-thought depth and problem selection.
- Assumptions/dependencies: robust mapping between output length and pedagogical difficulty; safeguards against gaming via verbose outputs; reliable detection of true reasoning vs. hallucination.
- Inference governance for production reasoning systems [Software, AI/ML]
- Implement policies that cap or escalate test-time scaling based on real-time accuracy indicators; combine majority voting, verifier checks, and confidence scoring to manage latency and cost while preserving reliability.
- Tools: “Inference Governor” orchestrating sampling count (k), output-length limits, and verification layers.
- Assumptions/dependencies: accurate online metrics; user-tolerance for latency; integration with product telemetry and cost controls.
- Monitoring AI progress via unsaturated, hard benchmarks [Policy, Academia]
- Track longitudinal improvements in reasoning using AMO-Bench-like suites that avoid saturation, informing national AI progress reports, funding priorities, and risk assessments for advanced systems.
- Tools: “Reasoning Progress Observatory” aggregating accuracy, pass@k, and token usage trends across model generations.
- Assumptions/dependencies: stable benchmark governance; regular releases of new, uncontaminated items; public transparency from AI vendors.
- Data ecosystem services for high-integrity benchmark curation [AI/ML, Policy]
- Offer third-party services that certify benchmark originality and difficulty using multi-expert cross-validation and leakage checks, helping journals, labs, and competitions maintain high evaluation standards.
- Products: “Benchmark Integrity Certification” for datasets and leaderboards.
- Assumptions/dependencies: trusted certifiers; accessible tooling; alignment incentives for dataset creators and model vendors.
Glossary
- AIME: The American Invitational Mathematics Examination, a U.S. high school contest often used in math reasoning benchmarks. "e.g., HMMT and AIME"
- AVG@32: An evaluation metric that averages performance over 32 sampled runs per model to reduce variance. "reported the average performance of these 32 results as the final metric (denoted as AVG@32)."
- Blind review: A quality control process where reviewers assess content without knowing the authors, reducing bias. "Each candidate problem undergoes blind review by at least three experts to assess its quality."
- Combinatorics: A branch of mathematics focused on counting, arrangement, and structure, used as a problem category. "and Combinatorics (12/50)."
- Compositional reasoning: The capability to solve problems by composing multiple reasoning steps or subskills. "with a particular focus on long-range and compositional reasoning"
- Context length: The maximum number of tokens a model can consider in its input/output during inference. "We configure the maximum context/output length to the highest allowable limit for each model during inference."
- Cross-validation: Verification by multiple experts to ensure correctness and consistent difficulty. "Each problem has undergone rigorous cross-validation by multiple experts to ensure it meets at least the difficulty standards of IMO."
- Data memorization: When models recall seen data rather than generalize, potentially inflating benchmark performance. "prevent potential performance leakages from data memorization."
- Descriptive answers: Open-form answers requiring textual explanation or case analysis rather than a single value. "For problems requiring descriptive answers (11 out of 50), we use LLM-based grading with o4-mini (Low) serving as the grading model."
- Difficulty filtering: An automated pre-screening using strong models to remove problems that are too easy. "We also incorporate an LLM-based difficulty filtering stage to exclude questions that do not present sufficient challenge to current reasoning models."
- Difficulty review: A human expert stage ensuring problems meet or exceed a specified difficulty threshold. "we implement a difficulty review stage to filter out problems lacking adequate complexity"
- Final-answer based grading: An evaluation approach that scores only the final answer, enabling automated grading. "Final-answer based grading. Each problem in AMO-Bench requires a final answer rather than a full proof, enabling efficient automatic grading."
- HMMT: The Harvard-MIT Mathematics Tournament, a high-level competition source for benchmark problems. "(e.g., HMMT and AIME)"
- Human-annotated reasoning paths: Expert-written step-by-step solutions included for transparency and analysis. "Human-annotated reasoning paths. In addition to the final answer, each problem also includes a detailed reasoning path written by human experts."
- Inference budget: The computational allowance at inference (e.g., output tokens) devoted to reasoning. "This indicates that further increasing the inference budget will further drive improvements on AMO-Bench."
- International Mathematical Olympiad (IMO): The premier global high school math competition used as a difficulty standard. "at least the International Mathematical Olympiad (IMO) difficulty standards"
- LLM-based grading: Using a LLM as a grader to judge equivalence or correctness of answers. "LLM-based grading provides greater flexibility across diverse answer types but may be less efficient and does not consistently guarantee accuracy."
- Majority voting: Aggregating multiple grader outputs by selecting the most frequent verdict for robustness. "majority voting is performed across five independent grading samples for each response."
- MO-level: Refers to Mathematical Olympiad level difficulty typical of contests like IMO. "MO-level competitions such as IMO."
- Numerical answers: Problems whose solutions are single numbers, enabling parser-based automatic checking. "For problems requiring numerical, set, or variable-expression answers (39 out of 50), we employ the parser-based grading."
- Originality review: Procedures to ensure problems are novel and not adaptations of existing materials. "The originality review stage aims to ensure that these newly created problems are not mere rewrites of publicly available materials, but demonstrate genuine originality."
- Parser-based grading: Rule-based or programmatic checking of answers (e.g., numeric/set equivalence) for efficiency and accuracy. "Parser-based grading offers high efficiency and accuracy when the model's response can be successfully parsed"
- pass@32: The probability of success when taking the best of 32 sampled outputs; a test-time sampling success metric. "pass@32 rates exceeding 70\%"
- pass@k: The chance that at least one of k independent samples is correct; reflects model potential under multiple attempts. "the pass@ performance of the model can reflect its inherent potential"
- Performance leakage: Artificial performance inflation due to exposure to similar training data or prior publication. "performance leakages from data memorization."
- Performance saturation: When benchmark scores approach a ceiling, reducing its ability to differentiate strong models. "due to performance saturation (e.g., AIME24/25)."
- Post-hoc analysis: Analysis conducted after observing results to interpret or validate findings. "Here, we offer a post-hoc analysis of benchmark difficulty based on the relationship between model performance and model output length."
- Post-processing algorithms: Additional parsing or transformation steps applied to model outputs to aid grading. "and adjust the post-processing algorithms."
- Proof-based: Problems requiring formal proofs rather than final numeric or closed-form answers. "these questions tend to be proof-based and require manual verification by experts"
- Reinforcement learning: A learning paradigm where models optimize behavior via reward signals, often used to improve reasoning. "further improvement through reinforcement learning."
- Sampling temperature: A stochastic decoding parameter controlling randomness when generating outputs. "We set the temperature of sampling to 1.0 for reasoning models and 0.7 for non-reasoning models."
- Set answers: Problems whose solutions are sets, requiring equivalence checking beyond simple numerics. "set answers (e.g., Example~\ref{exmp:set_answer})"
- Test-time compute: The computational resources expended during inference (e.g., tokens generated) to improve accuracy. "a promising scaling trend with increasing test-time compute on AMO-Bench."
- Test-time scaling: Improving performance by increasing inference-time sampling or output length without changing training. "indicating continued benefits from test-time scaling."
- Token budget: The limit on tokens available for model input and output during inference. "due to restrictions on the token budget."
- Tokenizer: The component that splits text into tokens used by the model and for length measurement. "We use the tokenizer of DeepSeek-V3.1 model to count tokens in solutions."
- Top-k sampling: A decoding strategy that samples from the top k most probable tokens at each step. "we use top-k=50 and top-p=0.95 during sampling."
- Top-p sampling: Nucleus sampling that chooses from the smallest set of tokens whose cumulative probability exceeds p. "we use top-k=50 and top-p=0.95 during sampling."
- USAMO: The United States of America Mathematical Olympiad, a national proof-based contest. "such as the IMO and USAMO."
- Variable-expression answers: Answers expressed as symbolic formulas or expressions rather than singleton values. "variable-expression answers (e.g., Example~\ref{exmp:variable_answer} which requires providing the general formula for an arithmetic sequence)"
Collections
Sign up for free to add this paper to one or more collections.