LoRAQuant: Mixed-Precision Quantization of LoRA to Ultra-Low Bits (2510.26690v1)

Abstract: Low-Rank Adaptation (LoRA) has become a popular technique for parameter-efficient fine-tuning of LLMs. In many real-world scenarios, multiple adapters are loaded simultaneously to enable LLM customization for personalized user experiences or to support a diverse range of tasks. Although each adapter is lightweight in isolation, their aggregate cost becomes substantial at scale. To address this, we propose LoRAQuant, a mixed-precision post-training quantization method tailored to LoRA. Specifically, LoRAQuant reparameterizes each adapter by singular value decomposition (SVD) to concentrate the most important information into specific rows and columns. This makes it possible to quantize the important components to higher precision, while quantizing the rest to ultra-low bitwidth. We conduct comprehensive experiments with LLaMA 2-7B, LLaMA 2-13B, and Mistral 7B models on mathematical reasoning, coding, and summarization tasks. Results show that our LoRAQuant uses significantly lower bits than other quantization methods, but achieves comparable or even higher performance.

• The paper introduces SVD-based splitting of LoRA adapters to concentrate key information and enable aggressive ultra-low bit quantization.
• It employs mixed-precision quantization with gradient-based optimization to preserve performance across various LLM benchmarks.
• The approach enhances memory efficiency in multi-tenant serving scenarios, facilitating scalable and cost-effective LLM customization.

LoRAQuant: Mixed-Precision Quantization of LoRA to Ultra-Low Bits

Introduction and Motivation

The proliferation of Low-Rank Adaptation (LoRA) for parameter-efficient fine-tuning of LLMs has enabled scalable customization for diverse tasks and users. However, the aggregate memory footprint of simultaneously loaded LoRA adapters becomes a bottleneck in multi-tenant LLM serving scenarios. Existing quantization methods, while effective for full model weights, are suboptimal for LoRA due to its unique low-rank structure and the need for ultra-low bitwidth quantization. LoRAQuant addresses this by introducing a mixed-precision post-training quantization scheme specifically tailored for LoRA adapters, leveraging SVD-based reparameterization to concentrate information and enable aggressive bitwidth reduction without significant performance degradation.

Methodology

SVD-Based Sub-LoRA Splitting

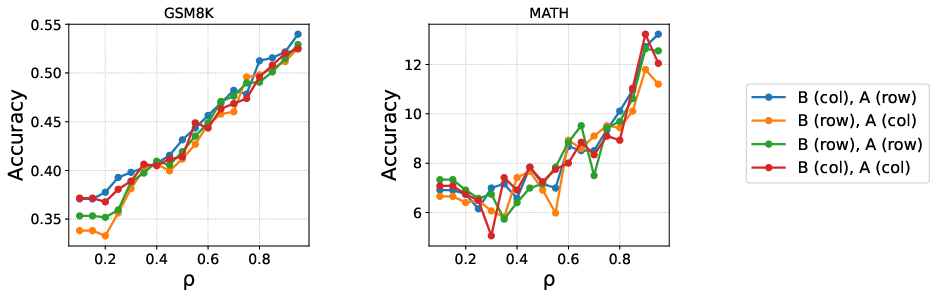
LoRAQuant decomposes each LoRA adapter $\mathbf{B}\mathbf{A}$ into two sub-adapters via truncated SVD:

$$\mathbf{B}\mathbf{A} = \mathbf{U}\mathbf{S}\mathbf{V}^\top$$

The reparameterization $\mathbf{B}' = \mathbf{U}\mathbf{S}^{1/2}$, $\mathbf{A}' = \mathbf{S}^{1/2}\mathbf{V}^\top$ ensures that singular values rank the importance of each component. The top-$h$ singular directions (determined dynamically by a coverage ratio $\rho$) are assigned to a high-precision sub-LoRA, while the remaining $r-h$ directions are relegated to a low-precision (1-bit) sub-LoRA.

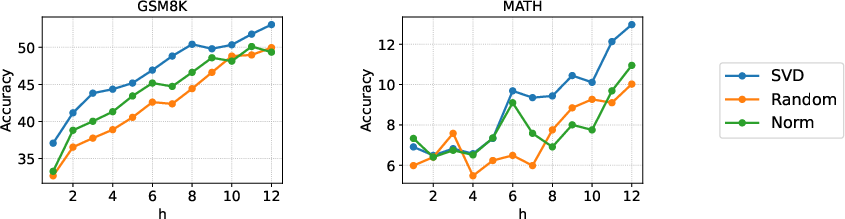
Figure 1: QuantizeLora algorithm overview, illustrating SVD-based splitting and mixed-precision quantization of LoRA adapters.

Mixed-Precision Quantization

• High-Precision Sub-LoRA: Quantized using RTN (Round-To-Nearest) at 2 or 3 bits per weight, with group-wise scaling and zero-point offsets.
• Low-Precision Sub-LoRA: Quantized using sign-based binarization ($\{-S, +S\}$), with scaling factors minimizing Frobenius norm reconstruction error.

Gradient-based optimization (using STE) is applied to each singular dimension to minimize quantization error prior to discretization, further improving representational fidelity.

Dynamic Bitwidth Allocation

The selection of $h$ (number of high-precision components) is governed by the ratio $\rho$ of total singular value energy preserved:

$$\frac{\sum_{i=1}^h s_i^2}{\sum_{i=1}^r s_i^2} \geq \rho$$

This adaptive strategy ensures that layers requiring greater representational capacity receive more precision, outperforming static or norm-based allocation.

Figure 2: Comparison of $h$ selection strategies, demonstrating superior performance of dynamic ratio-based allocation over static approaches.

Experimental Results

Benchmarks and Setup

LoRAQuant is evaluated on LLaMA 2-7B, LLaMA 2-13B, and Mistral 7B across GSM8K (math reasoning), MATH, HumanEval (code generation), and XSum (summarization). LoRA adapters are trained per task, and quantization is applied post-training. Metrics include pass@1 accuracy for math/code and ROUGE-L for summarization.

Performance and Bitwidth Trade-offs

LoRAQuant achieves competitive or superior task performance compared to state-of-the-art quantization baselines (GPTQ, PB-LLM, BiLLM) at substantially lower average bitwidths (often $<$2 bits/parameter). Notably, binary quantization and 1-bit RTN collapse performance, while LoRAQuant maintains high accuracy even under extreme compression.

• LLaMA 2-7B, GSM8K: LoRAQuant ([email protected]$) achieves 51.25% accuracy at 1.65 bits, outperforming PB-LLM and BiLLM at higher bitwidths.
• Mistral 7B, HumanEval: LoRAQuant ([email protected]$) reaches 39.63% at 1.97 bits, matching or exceeding baselines.

Ablation and Analysis

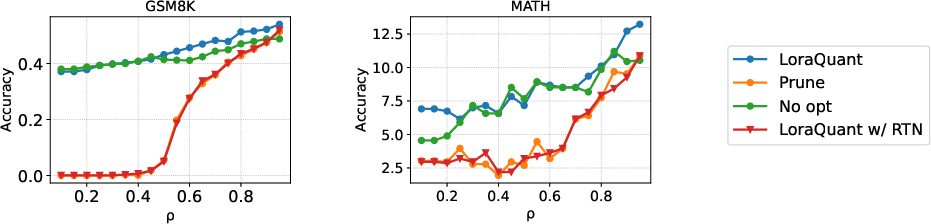
Figure 3: Ablation paper on optimization and quantization, showing the necessity of both SVD-based splitting and gradient-based optimization for maximal performance.

• Sub-LoRA Splitting: SVD-based splitting outperforms random and norm-based strategies, confirming the importance of concentrating information via singular values.
• Optimization: Gradient-based reparameterization yields consistent gains, especially at higher $\rho$.
• Pruning: Removing the low-precision sub-LoRA degrades performance, validating its contribution even at 1-bit quantization.
• Quantization Direction: Column-wise quantization of $\mathbf{B}'$ and row-wise quantization of $\mathbf{A}'$ is optimal for most tasks.

  Figure 4: Study on column-wise and row-wise quantization, supporting the default configuration for LoRAQuant.

Memory Efficiency

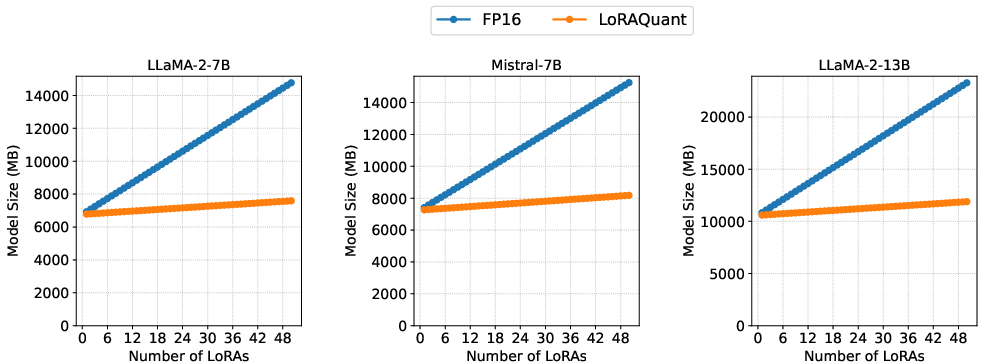
Figure 5: Memory usage scaling with number of loaded LoRAs, demonstrating LoRAQuant's substantial savings over FP16 as adapter count increases.

LoRAQuant's memory footprint grows sublinearly with the number of adapters, enabling practical multi-tenant LLM serving on resource-constrained hardware.

Implementation Considerations

• Computational Overhead: SVD and per-dimension optimization are efficient due to low LoRA rank ($r=16$), with optimization converging in $\sim$100 steps.
• Scalability: Each LoRA is quantized independently, facilitating parallelization and deployment at scale.
• Integration: LoRAQuant is compatible with standard QLoRA pipelines; base models can be quantized separately.
• Limitations: The method is specific to low-rank adapters; extension to full-rank matrices would require additional truncation and is nontrivial.

Implications and Future Directions

LoRAQuant enables aggressive memory reduction for multi-adapter LLM customization without sacrificing task performance, making it suitable for large-scale, multi-tenant deployments. The SVD-based mixed-precision paradigm may inspire analogous approaches for other structured model components. Future work could explore generalization to full model weights, integration with hardware-aware quantization, and commercial-scale validation.

Conclusion

LoRAQuant introduces a principled, SVD-driven mixed-precision quantization framework for LoRA adapters, achieving ultra-low bitwidths with minimal performance loss. Through dynamic allocation, specialized quantization, and efficient optimization, it sets a new standard for memory-efficient LLM customization. The approach is robust, scalable, and readily applicable to real-world multi-adapter serving scenarios, with potential for further extension and integration in the broader quantization landscape.