Efficient magic state cultivation with lattice surgery (2510.24615v1)

Abstract: Magic state distillation plays a crucial role in fault-tolerant quantum computation and represents a major bottleneck. In contrast to traditional logical-level distillation, physical-level distillation offers significant overhead reduction by enabling direct implementation with physical gates. Magic state cultivation is a state-of-the-art physical-level distillation protocol that is compatible with the square-grid connectivity and yields high-fidelity magic states. However, it relies on the complex grafted code, which incurs substantial spacetime overhead and complicates practical implementation. In this work, we propose an efficient cultivation-based protocol compatible with the square-grid connectivity. We reduce the spatial overhead by avoiding the grafted code and further reduce the average spacetime overhead by utilizing code expansion and enabling early rejection. Numerical simulations show that, with a color code distance of 3 and a physical error probability of $10^{-3}$, our protocol achieves a logical error probability for the resulting magic state comparable to that of magic state cultivation ($\approx 3 \times 10^{-6}$), while requiring about half the spacetime overhead. Our work provides an efficient and simple distillation protocol suitable for megaquop use cases and early fault-tolerant devices.

• The paper introduces MSC-LS, a protocol that reduces spacetime overhead by nearly 50% and achieves a logical error probability of 1.6×10⁻⁶ for magic state distillation.
• The methodology leverages lattice surgery and the rotated surface code, incorporating early rejection via a lookup table to optimize resource usage.
• The paper demonstrates practical implications for near-term fault-tolerant quantum devices, ensuring compatibility with square-grid architectures like superconducting qubits.

Efficient Magic State Cultivation with Lattice Surgery: Protocol, Implementation, and Implications

Introduction

Magic state distillation is a critical subroutine in fault-tolerant quantum computation, enabling the implementation of non-Clifford gates such as the $T$ gate. The resource overhead associated with distillation remains a major bottleneck for scalable quantum computing. The paper introduces a protocol—magic state cultivation with lattice surgery (MSC-LS)—that achieves high-fidelity magic state preparation with reduced spacetime overhead, leveraging the rotated surface code and lattice surgery techniques. The protocol is designed for compatibility with square-grid connectivity, which is essential for superconducting qubit architectures and other platforms with limited qubit mobility.

Background and Motivation

Traditional distillation protocols operate at the logical level, incurring significant overhead due to the need for fault-tolerant gate protection. Physical-level distillation, as pioneered by Goto and others, reduces this overhead by operating with noisy Clifford gates and detecting single gate errors, achieving logical error probabilities of $\mathcal{O}(p_\mathrm{phys}^2)$. Magic state cultivation (MSC) further improves fidelity via postselection and prepares magic states in a 2D color code, subsequently transformed into a grafted code for compatibility with matching decoders. However, the grafted code introduces substantial spacetime overhead due to high-weight stabilizers and complex implementation requirements.

MSC-LS addresses these limitations by:

• Avoiding the grafted code in favor of the rotated surface code.
• Employing lattice surgery for state transfer.
• Utilizing code expansion and early rejection via a lookup table to minimize average spacetime overhead.

Protocol Overview

MSC-LS consists of the following stages:

1. Injection and Cultivation: A magic state is injected non-fault-tolerantly into a distance-3 2D color code. Hadamard tests are performed to increase the fault distance, with postselection applied after each syndrome extraction.
2. Lattice Surgery Transfer: The encoded magic state is teleported from the color code to a rotated surface code of intermediate distance ($d_\mathrm{intermediate}$) using lattice surgery. This involves initializing the surface code, performing $Z_LZ_L$ measurements, and measuring the color code qubits in the $X$ basis.

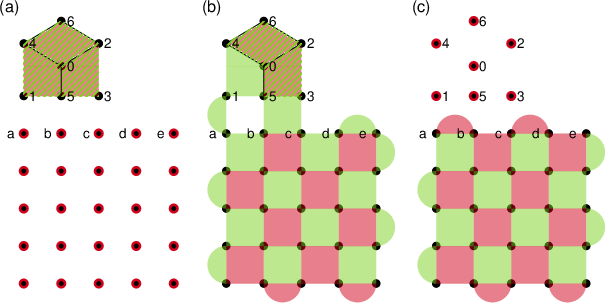
   Figure 1: Lattice surgery operation to teleport a magic state from the 2D color code of distance 3 to the rotated surface code of distance 5. X and Z stabilizers are measured, with postselection applied to critical outcomes.

3. Code Expansion: The rotated surface code is expanded from $d_\mathrm{intermediate}$ to $d_\mathrm{final}$ using Li's protocol, with additional rounds of syndrome extraction for code stabilization.

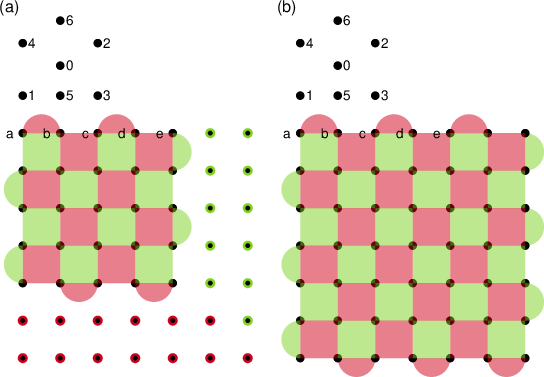
   Figure 2: Surface code expansion from distance 5 to distance 7, showing initialization and stabilizer placement for new qubits.

4. Early Rejection via Lookup Table: Prior to code expansion, a lookup table constructed from simulation data is used to reject distillation attempts likely to fail final postselection, reducing average resource consumption.

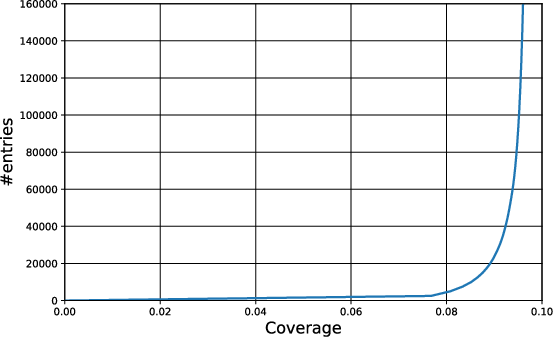
   Figure 3: Coverage of the lookup table, illustrating the trade-off between table size and the fraction of distillation attempts rejected early.

5. Final Postselection: After code stabilization, the complementary gap is computed using the MWPM decoder, and final postselection is performed to ensure high-fidelity output.

Implementation Details

Lattice Surgery

The lattice surgery procedure is designed to preserve the fault distance of the magic state during transfer. The protocol uses error-detecting syndrome extraction on the color code and error correction on the surface code. The merged code construction avoids high-weight stabilizers, except for a single six-weight $X$ stabilizer, which is skipped to minimize overhead. The procedure is compatible with matching decoders by assigning zero error probability to color code qubits post-transfer.

Code Expansion

Downward expansion is implemented for simplicity, though upward expansion offers better packing efficiency. Each new qubit is initialized to $\ket{0}$ or $\ket{+}$ as appropriate, and stabilizers are measured in subsequent rounds. The protocol requires $d_\mathrm{color}$ rounds of syndrome extraction after expansion to stabilize the code.

Lookup Table Construction

The lookup table is built by sampling error syndromes prior to code expansion and recording those that consistently lead to rejection in final postselection. The table enables immediate rejection of distillation attempts with syndromes above a threshold, reducing the need for additional rounds and qubit usage.

Numerical Results

Simulations using Stim and PyMatching demonstrate the following:

• Logical Error Probability: For $p_\mathrm{phys} = 10^{-3}$ and $d_\mathrm{color} = 3$, MSC-LS achieves a logical error probability of $1.6 \times 10^{-6}$ for $S\ket{+}$ distillation, matching the performance of MSC while halving the spacetime overhead.

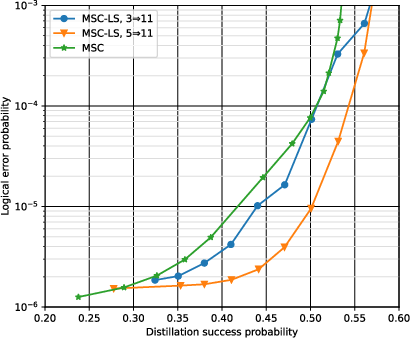
  Figure 4: Logical error probability of the resulting magic state as a function of distillation success probability for different protocol variants.

• Spacetime Overhead: In the logical error probability range $[10^{-6}, 10^{-5}]$, MSC-LS requires less than half the spacetime overhead of MSC. The lookup table further reduces overhead by 15% in the high-fidelity regime.

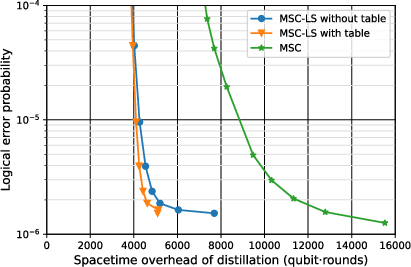
  Figure 5: Spacetime overhead of MSC-LS with and without the lookup table, compared to MSC.

• Resource Usage: The protocol maintains low qubit usage in early rounds via intermediate code distance and early rejection, with survival probability and qubit usage profiles confirming efficient resource allocation.

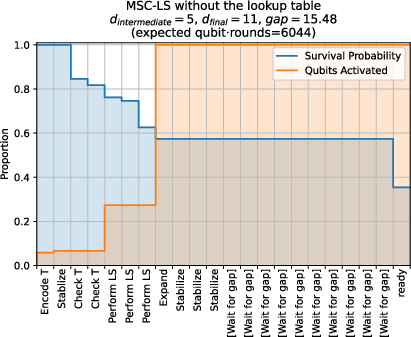
  Figure 6: Qubit usage and survival probability during distillation without the lookup table.

  

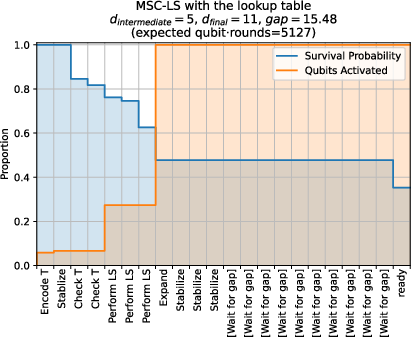
  Figure 7: Qubit usage and survival probability during distillation with the lookup table, showing improved early rejection.

Trade-offs and Limitations

MSC-LS achieves significant overhead reduction by:

• Avoiding the grafted code and its associated complexity.
• Using intermediate code distances to minimize qubit usage in early rounds.
• Enabling early rejection to reduce average spacetime cost.

However, the protocol requires additional rounds of syndrome extraction for code stabilization after expansion, and the end-to-end success probability remains relatively low, necessitating parallelization and pipelining for practical deployment. The current implementation focuses on $d_\mathrm{color} = 3$; scaling to larger code distances may require further optimization and analysis.

Practical and Theoretical Implications

MSC-LS is well-suited for near-term fault-tolerant devices and megaquop-scale quantum computers, where resource efficiency and hardware compatibility are paramount. The protocol leverages existing compiler and hardware support for the rotated surface code and lattice surgery, facilitating integration into current quantum computing stacks. The use of lookup tables for early rejection is particularly advantageous for memory-constrained systems.

Theoretically, the protocol demonstrates that physical-level distillation can match logical-level fidelity with substantially reduced overhead, challenging the necessity of complex code transformations in high-fidelity magic state preparation. The approach opens avenues for further optimization, including more sophisticated early rejection schemes and alternative code expansion strategies.

Future Directions

Key areas for future research include:

• Extending MSC-LS to larger color code distances and evaluating efficiency relative to MSC.
• Developing robust distillation pipelines with improved parallelization and pipelining capabilities.
• Investigating alternative code expansion schemes, including upward expansion and hybrid approaches.
• Enhancing lookup table construction with machine learning or advanced statistical methods to further reduce memory requirements and improve prediction accuracy.

Conclusion

Magic state cultivation with lattice surgery provides an efficient, practical protocol for high-fidelity magic state distillation, achieving comparable logical error probabilities to existing methods with approximately half the spacetime overhead. The protocol's simplicity, compatibility with square-grid connectivity, and support for early rejection make it a strong candidate for deployment in early fault-tolerant quantum devices and large-scale quantum computing architectures. Further research into scaling, pipeline integration, and advanced rejection strategies will be essential for realizing the full potential of this approach.