Transitive RL: Value Learning via Divide and Conquer (2510.22512v1)
Abstract: In this work, we present Transitive Reinforcement Learning (TRL), a new value learning algorithm based on a divide-and-conquer paradigm. TRL is designed for offline goal-conditioned reinforcement learning (GCRL) problems, where the aim is to find a policy that can reach any state from any other state in the smallest number of steps. TRL converts a triangle inequality structure present in GCRL into a practical divide-and-conquer value update rule. This has several advantages compared to alternative value learning paradigms. Compared to temporal difference (TD) methods, TRL suffers less from bias accumulation, as in principle it only requires $O(\log T)$ recursions (as opposed to $O(T)$ in TD learning) to handle a length-$T$ trajectory. Unlike Monte Carlo methods, TRL suffers less from high variance as it performs dynamic programming. Experimentally, we show that TRL achieves the best performance in highly challenging, long-horizon benchmark tasks compared to previous offline GCRL algorithms.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
What is this paper about?
This paper introduces a new way to teach robots (or game agents) how to reach any goal from any starting point using only recorded data. The method is called Transitive Reinforcement Learning (TRL). It uses a “divide-and-conquer” idea to learn faster and more reliably on very long tasks, like navigating a giant maze or solving a complex puzzle.
What questions did the researchers ask?
The paper explores simple versions of these questions:
- Can we design an offline learning method (using pre-recorded data only) that works well even when tasks take a very long time?
- Can we use a math rule called the “triangle inequality” (from shortest paths) to split long paths into two shorter, easier parts and then combine them?
- How can we avoid common problems in existing methods, like errors piling up (bias) or too much randomness (variance)?
- Does this new method actually perform better than popular approaches on tough tasks?
How does the method work?
Key ideas in everyday language
- Goal-conditioned RL: The agent learns a policy that, given a current state and a goal, picks actions to reach that goal as quickly as possible. Think of it as “get me from here to there in the fewest moves.”
- Offline learning: The agent trains entirely on a dataset of past attempts (no new exploration). Imagine learning to play a game only by watching recordings, without touching the controller.
- Triangle inequality: In a shortest-path sense, going from A to C is never longer than going from A to B plus B to C. In math terms: distance(A, C) ≤ distance(A, B) + distance(B, C). Here, B is a “subgoal” in the middle.
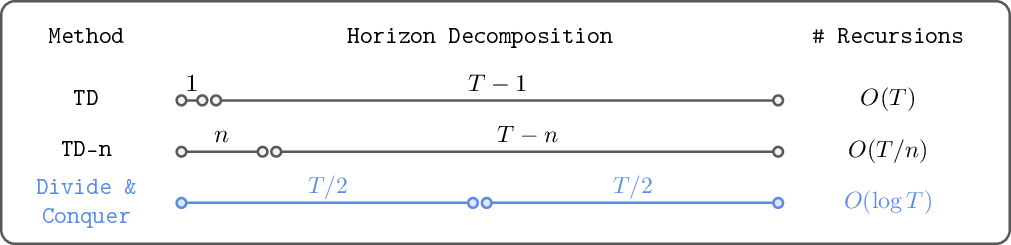
- Divide and conquer: To figure out how hard it is to reach the goal, TRL splits the journey into two halves at a subgoal, learns the value of each half, and then combines them. Doing this repeatedly can reduce the number of “passes” needed to learn from to , where is the length of the task. In plain terms: instead of walking a message through 1,000 steps one-by-one (and risking errors at each step), you combine halves, then quarters, etc., which needs far fewer steps.
Why not just use the usual methods?
- TD (Temporal Difference) learning: Think of this like passing a rumor along a long line—each pass adds a bit of error. Over very long tasks, these small errors stack up (bias accumulation), making the final result less reliable.
- MC (Monte Carlo) learning: This is like simulating the whole game many times to get an average outcome. It can be accurate, but for long tasks the results get very noisy (high variance).
TRL aims to avoid both problems by combining shorter, more trustworthy pieces.
The practical recipe
TRL adds a few tricks to make this idea work with neural networks:
- Soft “max” with expectile regression: Instead of taking a hard maximum over many possible subgoals (which can overestimate by grabbing a lucky mistake), TRL uses a soft version that leans toward higher values without going wild. You can think of it like aiming for high-scoring moves, but still keeping a cool head.
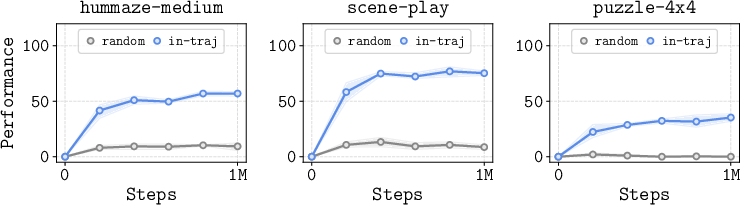
- In-trajectory subgoals: TRL only considers subgoals that actually appeared in the dataset trajectories (places the agent really visited), not imaginary points. This cuts down on bad guesses and keeps learning stable.
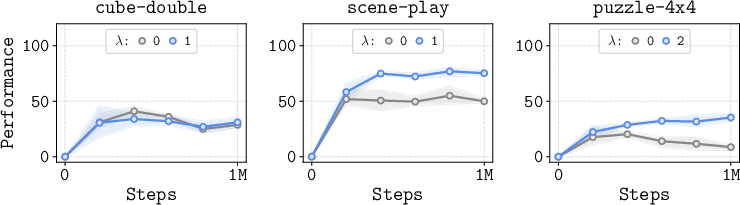
- Distance-based re-weighting: TRL gives more training attention to shorter chunks (easier, more accurate pieces) before trusting longer ones. This is like learning basic moves really well before trying long combos.
- Policy extraction: After learning values, TRL turns them into actions using either:
- A cautious optimizer that balances following the data with improving performance, or
- Rejection sampling, which picks from a set of plausible actions and chooses the one that looks best according to the learned values.
What did they find, and why is it important?
The researchers tested TRL on very challenging, long-horizon tasks, including:
- A giant humanoid maze where a robot with 21 joints must walk a complex route (test horizons up to 4000 steps).
- “Lights Out” style button puzzles with many steps and tricky dependencies.
They also tried TRL on standard goal-reaching benchmarks.
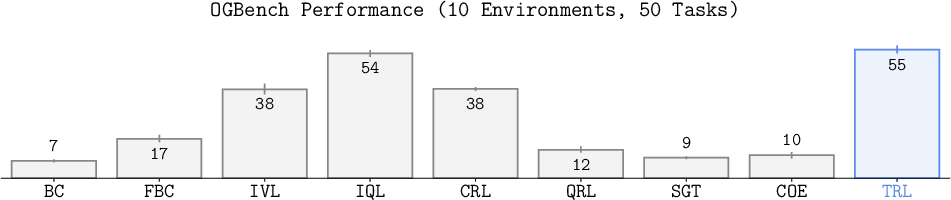
Main results:
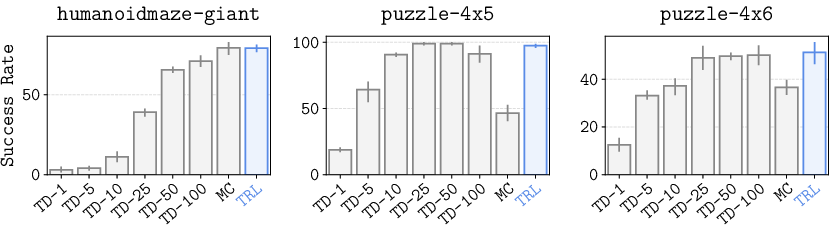
- TRL consistently outperformed or matched popular methods (TD, MC, and several goal-conditioned RL baselines) on the toughest long-horizon tasks.
- It reached strong success rates without needing to carefully tune extra settings like the number of TD steps (TD-), which other methods depend on.
- On standard tasks (not extremely long), TRL also did very well, often ranking near the top.
- Ablation studies showed:
- Using expectile regression (a soft max) is important on hard tasks.
- Only using in-trajectory subgoals (not random ones) matters a lot.
- Focusing training more on shorter chunks improves stability and performance.
Why this matters: TRL’s divide-and-conquer approach reduces error buildup and avoids high randomness, making it better suited for long, complex problems. Theoretically, its learning can require only about recursions in ideal cases, which is far fewer than traditional methods.
What does this mean for the future?
TRL shows that divide-and-conquer value learning is a promising path for scaling RL to long tasks using offline data. This could help train robots for complicated missions—like multi-room navigation, factory routines, or long manipulations—without needing huge amounts of online trial and error.
However, there are still open challenges:
- TRL mainly targets deterministic environments (where outcomes are predictable). Extending it to highly random settings (stochastic dynamics) while keeping values unbiased is an important next step.
- TRL focuses on goal-reaching. Adapting divide-and-conquer ideas to general reward-based RL (not just reaching a specific state) would be a big leap.
In short, TRL is a strong step toward RL methods that can handle long, complicated tasks more reliably, and it opens doors to new research on scalable, stable learning strategies.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
The following list highlights what remains missing, uncertain, or unexplored in the paper, with actionable directions for future work:
- Deterministic dynamics assumption: TRL relies on deterministic environments and hitting-time values; it remains unclear how to obtain unbiased, consistent value estimates and stable training under stochastic dynamics. Develop TRL variants leveraging successor temporal distances or other stochastic analogs and provide theoretical guarantees.
- Scope beyond goal-conditioned RL: The approach depends on the triangle inequality for hitting times. A generalization to reward-based (non-goal) RL is not provided. Define divide-and-conquer backups for arbitrary rewards and analyze their relation to Bellman operators and performance guarantees.
- Convergence under function approximation: The Floyd–Warshall-style optimality holds in tabular settings, but no convergence or error-bound analysis is given for TRL with neural function approximation, expectile regression, and in-sample subgoals. Provide conditions (e.g., dataset coverage, model class, optimization) under which TRL converges to near-optimal values and quantify approximation and bootstrapping error.
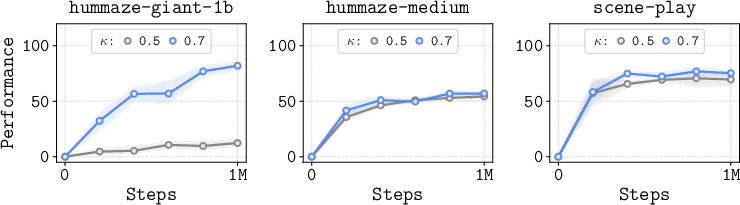
- Expectile parameter selection and theory: TRL replaces max with expectile regression but lacks a principled method to pick or adapt κ and lacks analysis of the bias introduced by κ<1. Derive bounds that relate κ to overestimation/underestimation, horizon-dependent bias accumulation, and stability, and design adaptive κ schedules.
- Distance-based re-weighting (λ) validity: The weighting uses current Q to estimate distance, potentially creating feedback loops and emphasizing poorly estimated samples. Provide theoretical justification for the weighting scheme, analyze its effect on convergence, and explore robust or adaptive alternatives (e.g., uncertainty-aware weighting, curriculum learning).
- Behavioral subgoals restriction: Limiting subgoals to in-trajectory states mitigates overestimation but may restrict optimality when datasets lack shortest-path coverage. Characterize conditions under which behavioral subgoals suffice, measure performance degradation with sparse or biased datasets, and design learned or planning-guided subgoal proposals that preserve stability.
- Continuous state spaces and goal matching: The paper assumes discrete states for notation; practical continuous settings require goal proximity thresholds or metric embeddings. Formalize TRL for continuous spaces (measure-theoretic foundations), define robust goal-matching criteria, and investigate representation learning that enforces (or approximates) the triangle inequality.
- Handling unreachable goals: No mechanism is described to detect or handle unreachable state–goal pairs (infinite distance). Develop estimators and training rules that identify unreachable goals, avoid spurious value propagation, and maintain stability.
- Base-case bootstrapping choices: Replacing short-horizon targets with γ{Δt} when Δt≤1 may introduce inconsistencies with learned Q under function approximation. Analyze the impact of these base cases on training bias and propose alternatives (e.g., learned one-step models, calibrated targets).
- Policy extraction robustness: DDPG+BC and rejection sampling are used, but guidance for choosing the BC coefficient α, sample count N, and generative model quality is task-specific. Provide principled selection criteria, sensitivity analyses, and guarantees for policy improvement and OOD robustness when extracting policies from TRL values.
- Scalability and compute: Experiments use 1B-sample datasets, but compute/memory footprint, training time, and efficiency relative to TD-n or MC are not reported. Quantify runtime complexity, memory usage, and energy costs; explore prioritized sampling or more efficient training pipelines for large-scale deployment.
- Empirical coverage requirements: Success likely depends on datasets containing paths connecting many state–goal pairs. Define coverage metrics (e.g., path-connectivity, subgoal density), diagnose failure modes under poor coverage, and design data collection or relabeling strategies that improve TRL’s effectiveness.
- Subgoal sampling strategy: Uniform sampling of k between i and j enables an O(log T) recursion result in tabular settings; the practical effect under function approximation and noisy targets is unquantified. Evaluate importance sampling, midpoint biasing, or learned subgoal distributions and relate them to horizon scaling and stability.
- Real-world robustness: Results are in simulation; robustness to sensor noise, stochastic dynamics, delays, and partial observability remains untested. Validate TRL on real robots, paper failure modes, and introduce modifications (e.g., belief-state TRL, noise-aware targets) to handle real-world uncertainty.
- Integration with planning/hierarchies: TRL is planning-free; combining it with planners or hierarchical policies could improve subgoal selection and horizon scaling. Investigate hybrid approaches that learn values via TRL while planning/selecting subgoals, and quantify benefits over pure TRL and pure planning.
- Representation learning for quasimetric structure: TRL presumes states admit a shortest-path-like structure. Develop representation learning methods that induce quasimetric consistency (triangle inequality) and paper how representation errors affect TRL’s backups and performance.
- Calibration and loss choice: BCE is used for Q-learning without analysis of calibration, especially for long horizons. Compare losses (BCE vs. MSE vs. margin losses), paper calibration and confidence, and assess their impact on policy extraction and over/underestimation.
- Theoretical sample complexity: No sample-complexity analysis is provided for TRL vs. TD-n/MC. Derive sample complexity or finite-sample bounds under realistic assumptions (function approximation, off-policy data, stochasticity) to substantiate scalability claims.
- Generalization to unseen goals: It’s unclear how well TRL extrapolates to goals not present in the dataset or far from observed trajectories. Measure out-of-distribution goal generalization, analyze failure modes, and propose mechanisms (e.g., generative augmentation, goal embeddings) to improve extrapolation.
Practical Applications
Practical, real-world applications of Transitive RL (TRL)
Below are actionable applications that follow directly from the paper’s findings, methods, and innovations. They prioritize deployments that benefit from TRL’s divide-and-conquer value learning, in-trajectory subgoal selection, expectile-based in-sample maximization, and distance-aware re-weighting for long-horizon, offline goal-conditioned control.
Immediate Applications
These can be piloted or deployed with current methods and infrastructure, assuming access to large offline datasets and predominantly deterministic dynamics.
- Long-horizon mobile robot navigation from logs
- Sector: robotics, logistics
- Use case: Train warehouse AMRs/AGVs to reliably reach specified waypoints across large facilities using historical navigation logs; reduce online exploration and brittle TD-n tuning.
- Tools/workflow: trajectory log ingestion → hindsight goal relabeling → TRL value learning with in-trajectory subgoals → policy extraction (DDPG+BC for smooth control).
- Assumptions/dependencies: near-deterministic motion and perception stack; broad state coverage in logs; sufficient compute to train on large datasets.
- Multi-step industrial manipulation (assembly, fixture alignment, panel/button sequences)
- Sector: robotics manufacturing
- Use case: Learn robust, long-horizon goal-reaching skills (e.g., multi-button panels, cable routing) from existing teleoperation or scripted production logs.
- Tools/workflow: TRL Q(s, a, g) with BCE loss; re-weighting favors short subproblems; rejection sampling for multi-modal actions (e.g., tool approaches).
- Assumptions/dependencies: consistent state/goal representation; well-curated and sufficiently large datasets; safety gating around deployment.
- Robotic process automation (RPA) for UI state-reaching
- Sector: software automation
- Use case: Train agents to reliably navigate complex enterprise UIs (reaching target screens or forms) from clickstream logs without runtime exploration.
- Tools/workflow: define state/goal as UI DOM states; TRL with in-sample subgoals; policy extraction via rejection sampling with a generative BC.
- Assumptions/dependencies: mostly deterministic UI transitions; instrumentation to encode states/goals; labeled or relabeled goals feasible from logs.
- Sim-to-real long-horizon training with minimal online finetuning
- Sector: robotics
- Use case: Generate large simulated trajectories (deterministic sim), train TRL to master long-horizon tasks (navigation/manipulation), then deploy with light calibration.
- Tools/workflow: simulator data fabrication → TRL training → domain randomization → small-scale on-robot validation.
- Assumptions/dependencies: manageable sim-to-real gap; sim determinism; reliable state-goal mapping across sim and real.
- Safer offline learning pipelines for regulated domains
- Sector: policy/regulatory, safety tooling
- Use case: Replace or reduce unsafe online exploration with offline TRL training; document data provenance and training behavior for audits.
- Tools/workflow: data governance + auditing; TRL’s lower overestimation risk via expectiles; reproducible training logs; evaluation on known tasks.
- Assumptions/dependencies: availability of high-quality offline datasets; conservative deployment policy; compliance processes for data and models.
- Game AI for puzzle- and long-horizon strategy tasks
- Sector: gaming/software
- Use case: Train NPCs to solve puzzle-like sequences (e.g., “Lights Out”-style or adventure game progression) using offline gameplay logs.
- Tools/workflow: encode states/goals, apply TRL with rejection sampling for multi-modal moves; evaluate generalization to new puzzles.
- Assumptions/dependencies: deterministic game state transitions; broad coverage of state space in logs.
- Digital twin training for facility operations (cleaning, inspection)
- Sector: industrial robotics
- Use case: Use deterministic twins to create large trajectory datasets; train TRL for goal-reaching routines (end-to-end cleaning routes, inspection circuits).
- Tools/workflow: twin data → TRL → deployment on robots; adapt BC constraints to robot capability and safety margins.
- Assumptions/dependencies: high-fidelity digital twin; clear mapping of twin states to real-world sensors; deterministic control stack.
- Drop-in module in RL platforms to stabilize long-horizon offline value learning
- Sector: software/ML tooling
- Use case: Integrate TRL components (in-trajectory subgoal sampler, expectile loss, distance-based re-weighting, policy extraction via DDPG+BC or rejection sampling) into PyTorch/TF RL pipelines to avoid TD bias accumulation and MC variance.
- Tools/workflow: packaged library with simple API for Q(s, a, g), hindsight relabeling, configurable expectile κ and re-weighting λ.
- Assumptions/dependencies: developers can encode goal-conditioned tasks; compatibility with existing BC/diffusion generators for rejection sampling.
Long-Term Applications
These require additional research, scaling, or productization, especially to address stochasticity, general rewards, safety, and standardization.
- Autonomous driving and mobile autonomy under significant stochasticity
- Sector: mobility/transport
- Vision: Extend TRL with successor temporal distances or probabilistic triangle inequality to handle noise, uncertainty, and partial observability.
- Tools/workflow: TRL+stochastic extensions; large-scale logged driving datasets; robust policy extraction with behavior regularization.
- Assumptions/dependencies: theoretical advances for unbiased value learning in stochastic domains; massive, curated logs; compliance with safety standards.
- Healthcare robots (surgical assistance, hospital logistics)
- Sector: healthcare
- Vision: Offline training of precise long-horizon goal-reaching behaviors (e.g., instrument handovers, multi-room delivery) with certified safety.
- Tools/workflow: regulated TRL stack; comprehensive dataset governance; simulation+tactile/visual logs; conservative policy extraction.
- Assumptions/dependencies: stringent validation, certification pathways; high-quality clinical datasets; deterministic operation phases.
- Energy systems and building controls
- Sector: energy/industrial automation
- Vision: Goal-reaching controllers for long sequences (e.g., multi-zone actuation targets, maintenance routines) under nontrivial uncertainty.
- Tools/workflow: TRL variants incorporating stochastic dynamics; digital twin integration; safety monitors; risk-aware deployment.
- Assumptions/dependencies: probabilistic extension of triangle inequality; reliable state encoding; standardized evaluation protocols.
- General reward-based RL beyond goal-conditioned hitting times
- Sector: ML/AI research, software
- Vision: Adapt divide-and-conquer value learning to generic Q-learning with shaped rewards and delayed sparse returns.
- Tools/workflow: new backup operators generalizing transitivity; hybrid planning-free Bellman rules that preserve O(log T) recursion.
- Assumptions/dependencies: fresh theory and algorithms; proofs of bias/variance behavior; benchmarks beyond goal-reaching.
- Hierarchical TRL with learned subgoal discovery
- Sector: robotics/ML research
- Vision: Jointly learn subgoals and policies to further compress horizons and improve sample efficiency on ultra-long tasks.
- Tools/workflow: discovery modules (e.g., clustering, option discovery), TRL-level backups over learned subgoal graphs; policy extraction with hierarchical constraints.
- Assumptions/dependencies: reliable subgoal discovery; stability under function approximation; scalability to multi-robot use.
- Multi-agent coordination for team goal-reaching
- Sector: robotics/swarm systems
- Vision: Extend TRL to joint state-goal spaces and cooperative backups for multi-agent navigation/manipulation.
- Tools/workflow: centralized or distributed TRL; communication-aware subgoal selection; rejection sampling across agents’ BC policies.
- Assumptions/dependencies: tractable joint state/action spaces; coordination protocols; robustness to combinatorial explosion.
- Robustness to OOD and noise with TRL-S (successor temporal distance)–style approaches
- Sector: ML research
- Vision: Combine TRL with successor temporal distances to mitigate bias/variance in stochastic settings while preserving divide-and-conquer benefits.
- Tools/workflow: successor-based value targets; conservatism constraints; evaluations on noisy long-horizon benchmarks.
- Assumptions/dependencies: new training objectives; stability on continuous spaces; principled handling of OOD actions.
- Standards and governance for offline RL datasets and training
- Sector: policy/regulatory, cross-industry consortia
- Vision: Define data collection, documentation, and audit standards for offline goal-conditioned training in safety-critical domains.
- Tools/workflow: template governance policies; dataset datasheets; reproducible TRL training records; certification criteria.
- Assumptions/dependencies: stakeholder buy-in; alignment with existing AI model governance; enforcement mechanisms.
- Edge deployment and model compression for on-device long-horizon control
- Sector: embedded systems/robotics
- Vision: Compress TRL-trained models for low-latency inference (e.g., ARM, DSP) while retaining long-horizon reliability.
- Tools/workflow: quantization/pruning/distillation of Q(s, a, g); latency-aware policy extraction; on-device hindsight relabeling for adaptation.
- Assumptions/dependencies: hardware constraints; acceptable accuracy-latency tradeoffs; local logging for updates.
- Finance and operations research for sequential decision-making
- Sector: finance/enterprise optimization
- Vision: Use TRL-inspired divide-and-conquer value learning on long planning horizons in simulated or low-variance settings.
- Tools/workflow: digital twins of markets or operations; conservative policy extraction; risk-aware constraints.
- Assumptions/dependencies: highly stochastic environments demand TRL extensions; strong governance and risk controls; simulation fidelity.
Notes on cross-cutting assumptions and dependencies:
- Determinism or low-stochasticity is central to the baseline TRL formulation; robust extensions are needed for highly stochastic systems.
- Large, diverse offline datasets with good state-space coverage are critical; data quality and goal relabeling matter.
- Goal-conditioned representation must align states and goals in the same space; hitting-time objectives should be well-defined.
- Function approximation stability depends on expectile regression choice (κ) and in-sample subgoal selection; distance-based re-weighting (λ) helps emphasize reliable short subproblems.
- Policy extraction should avoid out-of-distribution exploitation via behavior regularization (DDPG+BC) or sample-based rejection from a strong generative BC.
Glossary
- Absorbing state: A terminal state that, once entered, halts further transitions. "the agent enters an absorbing state upon reaching the goal"
- Action-value function: A function that estimates expected return from taking an action in a state toward a goal. "an action-value function :"
- Bellman backup: The recursive update of value functions using immediate reward plus discounted future value. "Bellman backups, "
- Bellman recursions: Repeated applications of Bellman updates across a trajectory. "reduce the number of Bellman recursions to "
- Behavior Cloning (BC): Supervised policy learning that imitates actions from a dataset. "goal-conditioned BC policy"
- Behavioral policy: The policy that generated the offline dataset of actions. "so that it can effectively capture the potentially multi-modal distributions of the behavioral policy"
- Behavioral subgoals: Subgoals restricted to states occurring within dataset trajectories. "restricting to behavioral subgoals is crucial"
- Binary cross-entropy (BCE): A loss function for binary targets commonly used to train classifiers. "we use the binary cross-entropy (BCE) loss"
- Bias accumulation: The compounding of estimation bias across recursive updates over long horizons. "bias accumulation"
- Bias-variance tradeoff: The balance between reducing bias and controlling variance in estimators. "strike a balance in the bias-variance tradeoff"
- Controlled Markov process: A state-transition system where actions control probabilistic dynamics. "We consider a controlled Markov process defined by a tuple $\gM = (\gS, \gA, p)$"
- Curse of horizon: The degradation of learning performance as task horizon lengthens. "the curse of horizon"
- DDPG+BC: A policy learning objective combining value maximization with behavior cloning regularization. "``DDPG+BC'' objective"
- Deterministic environments: Systems where next states are uniquely determined by current state and action. "In deterministic environments, we can define the notion of temporal distances."
- Diffusion models: Generative models that learn to denoise data via iterative stochastic processes. "diffusion models"
- Divide-and-conquer value learning: Learning values by combining solutions of smaller trajectory segments. "divide-and-conquer value learning"
- Dynamic programming: A method that solves complex problems by aggregating solutions to subproblems. "it performs dynamic programming"
- Expectile loss: A regression loss that emphasizes upper tails to approximate maximization. "expectile loss"
- Expectile regression: Asymmetric regression that approximates the max operator using expectiles. "The asymmetric expectile regression in \Cref{eq:iql_v} approximates the operator"
- Flow matching: A generative modeling approach that learns transport maps via differential equations. "flow matching"
- Floyd-Warshall algorithm: A dynamic programming method for computing all-pairs shortest paths. "Floyd-Warshall algorithm"
- Goal-conditioned reinforcement learning (GCRL): RL where the policy is conditioned on a desired goal state. "offline goal-conditioned RL (GCRL)"
- Hindsight relabeling: Rewriting goals in trajectories to states the agent actually reached. "hindsight relabeling"
- Hitting time: The number of steps until a goal is reached for the first time. "defined by hitting times"
- Implicit Q-Learning (IQL): An offline RL method that avoids querying out-of-distribution actions via expectile value updates. "IQL~\citep{iql_kostrikov2022}"
- In-sample maximization: Maximizing over values computed only from states/actions seen in the dataset. "in-sample maximization within in-sample subgoals"
- Jensen's inequality: A mathematical inequality relating convex functions and expectations. "Jensen's inequality"
- Monte Carlo (MC) returns: Value estimates computed from sampled trajectory returns without bootstrapping. "Monte Carlo (MC) returns"
- Offline reinforcement learning: Learning policies solely from fixed datasets without environment interaction. "offline reinforcement learning problem"
- Off-policy reinforcement learning: Learning a policy from data generated by a different behavior policy. "off-policy reinforcement learning (RL)"
- Out-of-distribution actions: Actions not represented in the dataset, which can cause value overestimation. "out-of-distribution actions"
- Quasimetric constraint: A structural constraint enforcing triangle inequality-like properties on value distances. "quasimetric constraint"
- Reparameterized gradients: Policy optimization by differentiating through sampled actions via reparameterization. "Reparameterized gradients"
- Rejection sampling: Selecting actions by sampling from a proposal policy and choosing the highest-value sample. "Rejection sampling"
- SARSA: An on-policy RL method estimating action values by sampling state-action-next-state-next-action. "behavioral (SARSA) goal-conditioned value function"
- Successor temporal distance framework: A stochastic extension that preserves triangle inequality-like structure for distances. "successor temporal distance framework"
- Target network: A slowly updated copy of a value network used for stable bootstrapping. "target network"
- Target Q function: The Q-function used to construct targets in Bellman updates. "the target Q function"
- Temporal difference (TD) learning: Bootstrapped value learning using recursive Bellman targets. "temporal difference (TD) learning"
- Temporal distance: The minimal number of steps required to reach a goal from a state. "The temporal distance "
- Transitive Bellman update: A value update that composes values via triangle inequality through subgoals. "transitive Bellman update rule"
- Triangle inequality: The property that distance from s to g is no more than via an intermediate subgoal. "triangle inequality"
- Value overestimation: Inflated value estimates, often due to maximizing over noisy predictions. "value overestimation"
Collections
Sign up for free to add this paper to one or more collections.