Visual Diffusion Models are Geometric Solvers (2510.21697v1)

Abstract: In this paper we show that visual diffusion models can serve as effective geometric solvers: they can directly reason about geometric problems by working in pixel space. We first demonstrate this on the Inscribed Square Problem, a long-standing problem in geometry that asks whether every Jordan curve contains four points forming a square. We then extend the approach to two other well-known hard geometric problems: the Steiner Tree Problem and the Simple Polygon Problem. Our method treats each problem instance as an image and trains a standard visual diffusion model that transforms Gaussian noise into an image representing a valid approximate solution that closely matches the exact one. The model learns to transform noisy geometric structures into correct configurations, effectively recasting geometric reasoning as image generation. Unlike prior work that necessitates specialized architectures and domain-specific adaptations when applying diffusion to parametric geometric representations, we employ a standard visual diffusion model that operates on the visual representation of the problem. This simplicity highlights a surprising bridge between generative modeling and geometric problem solving. Beyond the specific problems studied here, our results point toward a broader paradigm: operating in image space provides a general and practical framework for approximating notoriously hard problems, and opens the door to tackling a far wider class of challenging geometric tasks.

• The paper demonstrates that visual diffusion models transform noisy pixel inputs into accurate approximations for complex NP-hard geometric problems.
• It introduces a unified U-Net based approach applied to inscribed squares, Steiner trees, and maximum area polygonizations, validated with quantitative metrics.
• The method leverages stochastic denoising and post-processing to refine predictions and maintain high validity across varying problem scales.

Visual Diffusion Models as Geometric Solvers: A Technical Analysis

Introduction and Motivation

This paper establishes that standard visual diffusion models, when trained on pixel-space representations of geometric problems, can serve as effective solvers for a range of hard geometric tasks. The approach is fundamentally distinct from prior work that leverages parametric or symbolic representations; instead, it recasts geometric reasoning as conditional image generation. The authors demonstrate this paradigm on three canonical problems: the Inscribed Square Problem, the Euclidean Steiner Tree Problem, and the Maximum Area Polygonization Problem. Each is NP-hard or unsolved in the general case, and each admits a natural visual formulation.

Figure 1: Visual diffusion model uncovers diverse approximate solutions to the Inscribed Square Problem, with each solution corresponding to a different random seed.

Methodology: Visual Diffusion in Pixel Space

The core methodology involves training a conditional U-Net-based diffusion model to denoise random Gaussian samples into valid geometric solutions, conditioned on a visual representation of the problem instance. The conditioning image encodes the problem (e.g., a curve, set of points), while the target is a rasterized solution (e.g., square, tree, polygon). The model operates in pixel space, with no explicit geometric or combinatorial encoding.

Key architectural details:

• U-Net backbone with multi-head self-attention at bottleneck and intermediate levels.
• Two-channel input: noisy target and conditioning image.
• Sinusoidal time embeddings for diffusion step conditioning.
• Training via DDIM with 100 steps, $L_2$ noise prediction loss, AdamW optimizer, and mixed precision.

This approach is notable for its simplicity and generality: the same architecture and training procedure are used for all tasks, with only the training data varying.

Case Study 1: Inscribed Square Problem

The Inscribed Square Problem asks whether every Jordan curve contains four points forming a square. The model is trained on synthetic images of curves and their inscribed squares, with the curve as the conditioning channel and the square as the target.

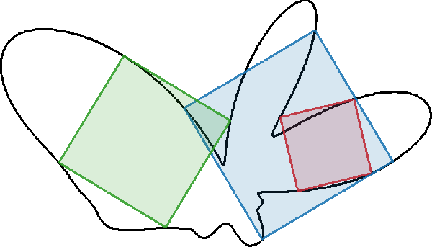
Figure 2: Example of a curve (black) with three inscribed squares, illustrating the multiplicity and diversity of valid solutions.

During inference, the model generates candidate squares via denoising, and a post-processing "snapping" step rigidly aligns the predicted square to the curve by maximizing the negative average corner-to-curve distance. Evaluation metrics include alignment score and squareness, both of which approach ground truth values after snapping.

Figure 3: Denoising progression for inscribed square predictions, showing refinement from noisy initialization to accurate geometric placement.

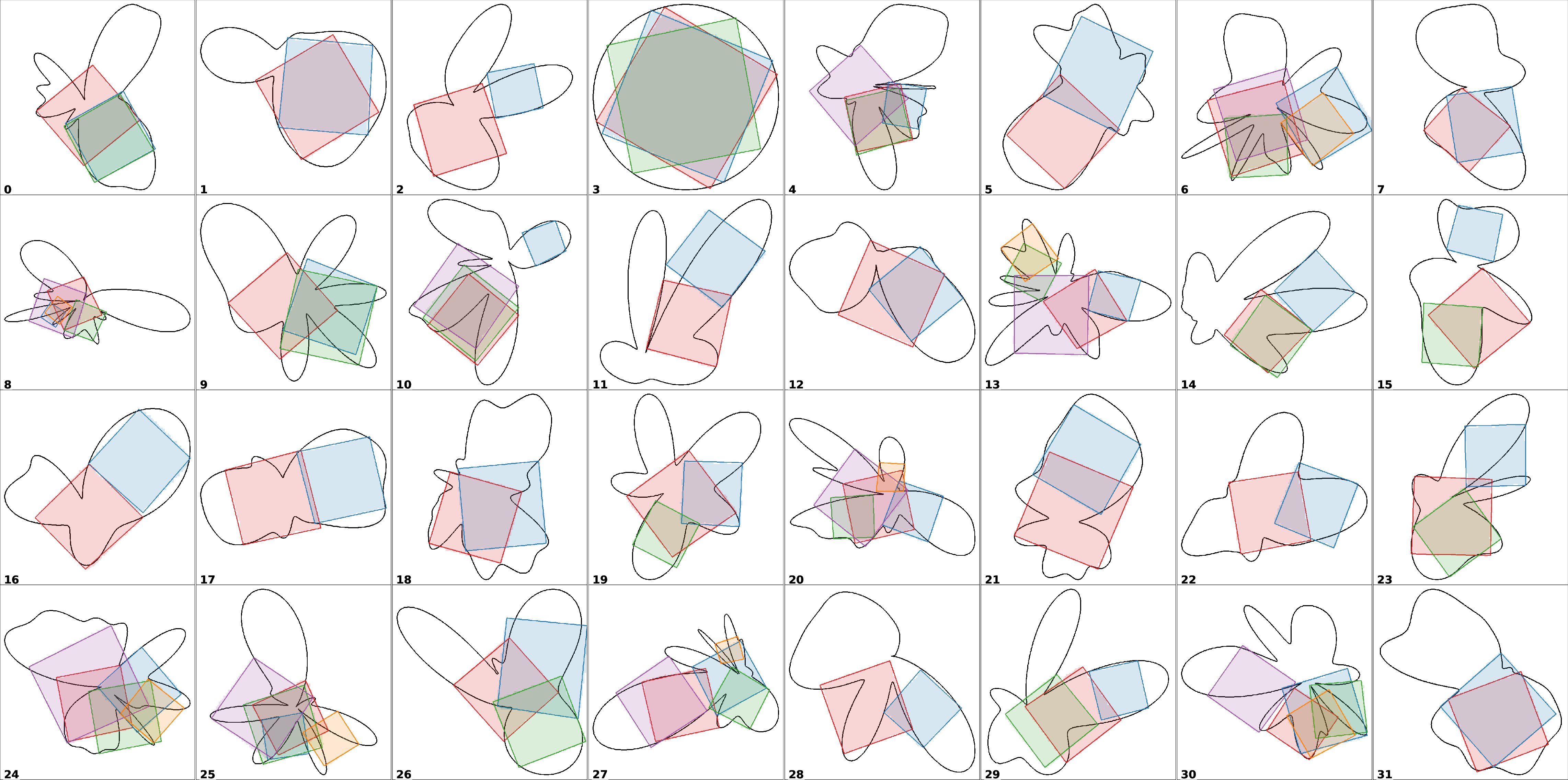
Figure 4: Diverse inscribed square solutions produced by the model for different Jordan curves.

The model reliably produces high-quality approximations, with minimal sub-pixel deviations attributable to rasterization. The stochasticity of diffusion enables sampling multiple distinct solutions per instance, capturing the multimodal nature of the problem.

Case Study 2: Steiner Tree Problem

The Euclidean Steiner Tree Problem seeks the shortest network connecting a set of points, possibly introducing auxiliary Steiner points. The model is trained on images of terminal points and their optimal Steiner trees, computed via GeoSteiner and rasterized.

Figure 5: Input terminal nodes (red) and corresponding Steiner Minimal Tree (dark gray Steiner points).

Inference involves extracting node and edge positions from the generated image via connected component analysis and edge pixel thresholding. Validity is checked by ensuring the output is a tree containing all terminals.

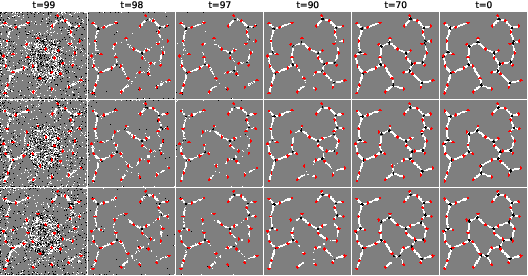
Figure 6: Denoising progression for Steiner tree predictions, illustrating the emergence of tree structure and refinement of connectivity.

Quantitative results show that the model achieves near-optimal tree lengths for up to 30 points, with a valid solution rate exceeding 98% for up to 30 points and competitive performance compared to MST and random baselines. For larger instances (41–50 points), the valid solution rate drops to 33%, indicating limitations in scaling and generalization.

Case Study 3: Maximum Area Polygonization

The Maximum Area Polygonization Problem asks for a simple polygon of maximal area passing through a given set of points. The model is trained on exhaustive optimal solutions for small point sets (7–12 points), with input points and polygon rasterized as conditioning and target images.

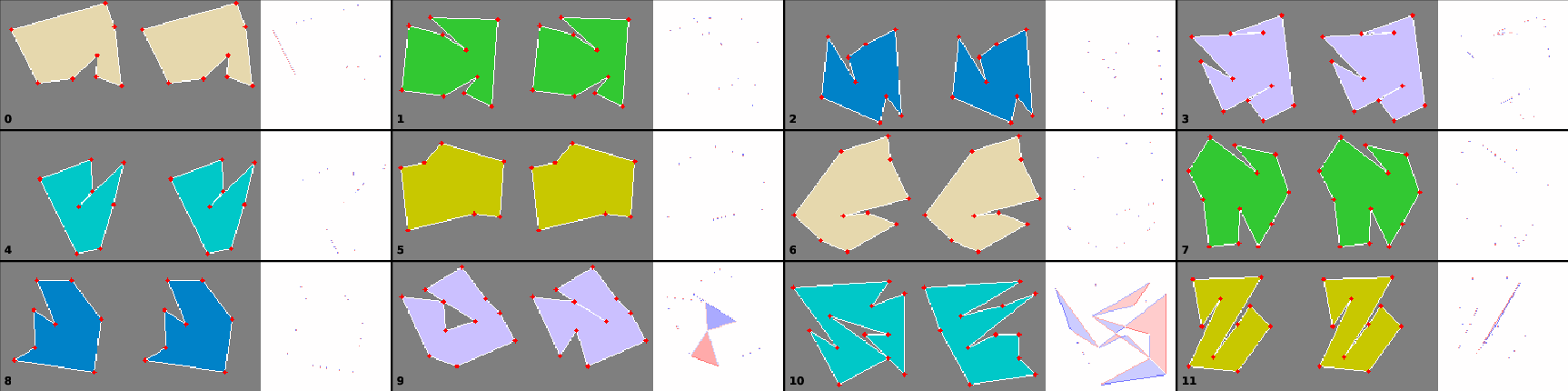
Figure 7: Comparison of optimal maximum area polygons (left), model predictions (middle), and area difference maps (right).

Polygon extraction from the output image involves edge validation and cycle detection, with tolerance for minor overlaps. The model achieves a valid polygon rate of 95% for 7–12 points, with mean area ratios above 0.98 compared to optimal solutions. For 13–15 points, the valid rate drops to 62%, but area ratios remain high when valid polygons are produced.

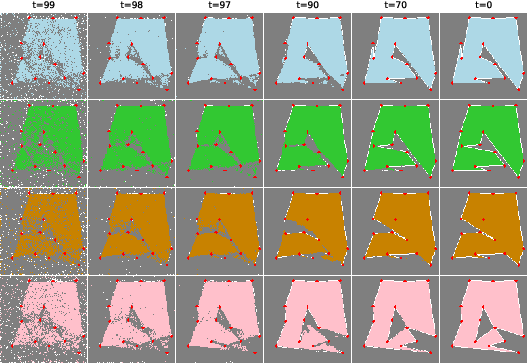
Figure 8: Denoising progression for maximum area polygon predictions, showing the evolution from noise to valid polygon structure.

A regression ablation demonstrates that diffusion models outperform direct regression in terms of robustness and valid solution rate, even for problems with unique solutions per instance.

Analysis of Denoising Dynamics

Across all tasks, the denoising process exhibits a consistent pattern: global geometric structure emerges early, with subsequent steps refining details. This suggests that low-frequency geometric features are prioritized, and that inference could be accelerated by allocating more steps to early timesteps. The stochasticity of diffusion enables exploration of solution space, which is particularly valuable for multimodal or ambiguous problems.

Practical and Theoretical Implications

Practically, the approach offers a unified framework for approximating solutions to a wide class of geometric problems, with minimal domain-specific engineering. The method generalizes to larger or more complex instances than those seen during training, though with diminishing validity rates as complexity increases. Theoretically, the results highlight the capacity of visual diffusion models to encode geometric reasoning in pixel space, bridging generative modeling and mathematical problem solving.

The main limitations are imposed by discretization artifacts, scalability to large input sizes, and the need for post-processing to extract symbolic solutions from images. The approach does not outperform specialized solvers for any single problem, but its generality and flexibility are notable.

Future Directions

Potential future developments include:

• Scaling to higher-resolution images and larger input sets via architectural or training advances.
• Integrating symbolic post-processing to improve solution extraction and validity.
• Extending to other geometric or combinatorial problems with natural visual representations.
• Exploring hybrid models that combine pixel-space diffusion with parametric or graph-based reasoning.

Conclusion

This work demonstrates that standard visual diffusion models, trained on pixel-space representations, can serve as effective solvers for hard geometric problems. The approach is general, simple, and capable of producing accurate and diverse solutions across multiple tasks. While not competitive with specialized solvers in efficiency or scalability, the paradigm opens new avenues for leveraging generative models in mathematical problem solving and geometric reasoning.