Fisher meets Feynman: score-based variational inference with a product of experts (2510.21598v1)
Abstract: We introduce a highly expressive yet distinctly tractable family for black-box variational inference (BBVI). Each member of this family is a weighted product of experts (PoE), and each weighted expert in the product is proportional to a multivariate $t$-distribution. These products of experts can model distributions with skew, heavy tails, and multiple modes, but to use them for BBVI, we must be able to sample from their densities. We show how to do this by reformulating these products of experts as latent variable models with auxiliary Dirichlet random variables. These Dirichlet variables emerge from a Feynman identity, originally developed for loop integrals in quantum field theory, that expresses the product of multiple fractions (or in our case, $t$-distributions) as an integral over the simplex. We leverage this simplicial latent space to draw weighted samples from these products of experts -- samples which BBVI then uses to find the PoE that best approximates a target density. Given a collection of experts, we derive an iterative procedure to optimize the exponents that determine their geometric weighting in the PoE. At each iteration, this procedure minimizes a regularized Fisher divergence to match the scores of the variational and target densities at a batch of samples drawn from the current approximation. This minimization reduces to a convex quadratic program, and we prove under general conditions that these updates converge exponentially fast to a near-optimal weighting of experts. We conclude by evaluating this approach on a variety of synthetic and real-world target distributions.
Summary
- The paper introduces a novel score-based variational inference method using a product of experts to approximate complex, non-Gaussian posteriors.
- It leverages Feynman parameterization for accurate and scalable normalizing constant estimation across diverse synthetic and real-world targets.
- Empirical results demonstrate robust performance on multimodal, heavy-tailed, and high-dimensional distributions, while also revealing challenges in expert selection.
Score-Based Variational Inference with a Product of Experts: Empirical Analysis and Implementation
Overview
The paper "Fisher meets Feynman: score-based variational inference with a product of experts" (2510.21598) presents a comprehensive empirical and methodological paper of score-based variational inference (VI) using a product of experts (PoE) family. The work leverages Feynman parameterization for efficient estimation of normalizing constants and importance sampling, and investigates the practicalities of expert selection, reweighting, and convergence in high-dimensional and non-Gaussian settings. The empirical results span synthetic targets and real-world posterior distributions, providing insights into the efficiency, scalability, and limitations of the PoE VI approach.
Empirical Study: Normalizing Constant and Sampling Procedure
The estimation of the normalizing constant is critical for PoE models, especially when the density is defined as a product of multiple expert distributions. The paper utilizes Monte Carlo estimation via Feynman parameterization, sampling from a Dirichlet distribution over expert weights . The accuracy of the normalizing constant estimate is benchmarked against a ground truth computed with 5 million samples, and the mean absolute error is reported across increasing sample sizes and random seeds.
The efficiency of the importance sampling procedure is quantified using the relative effective sample size (ESS), which measures the loss in sampling efficiency due to weight variability. High relative ESS values (above 0.8) are observed in low-dimensional, well-behaved cases, while efficiency drops (0.3–0.5) in scenarios with many sparsely weighted experts, indicating the need for larger sample sizes or improved expert selection strategies.
Figure 1: Example 1. Skew and heavy tails.
The figure illustrates the behavior of the normalizing constant estimation and sampling efficiency for a PoE density with skew and heavy tails, highlighting the robustness of the approach in challenging regimes.
Synthetic Target Distributions and Results
The paper evaluates the PoE VI method on a diverse set of synthetic targets, including Gaussian mixtures, multimodal PoE densities, diamond-shaped distributions, funnel models, Rosenbrock functions, and sinh-arcsinh distributions with skewness and heavy tails. Each target is carefully constructed to test the flexibility and expressiveness of the PoE family.
Additional results on the Rosenbrock and sinh-arcsinh targets demonstrate the method's ability to approximate complex, non-Gaussian posteriors in moderate and high dimensions (). The normalizing flow baseline is implemented using realNVP architectures, and hyperparameters are tuned via grid search to ensure fair comparison.
Experimental Setup and Implementation Details
All experiments are conducted on CPU, utilizing a 32-core Intel workstation with 503 GB RAM. The PoE VI code is implemented in Python, with quadratic programming solved via the jaxopt_osqp solver. Integrability constraints are enforced with a slack parameter, and batch sizes and learning rates are systematically varied to assess their impact on convergence and fit quality.
For baseline methods (ADVI, normalizing flows), the ELBO is optimized using Adam, with learning rates selected through pilot studies. The number of gradient evaluations is matched across methods to ensure comparability, and the computational cost is dominated by score evaluations of the target density.
Expert Selection and Sparsity
Expert selection is a key component of the PoE VI procedure. The heuristic involves placing a large number of experts and reweighting their importance during optimization. Empirical results indicate that, while a compact set of active experts leads to more efficient inference, the method remains robust even with many sparsely weighted experts, provided sufficient samples are used.
The summary table in the paper details the number of experts, active experts, and sampling parameters for each synthetic target, demonstrating the scalability of the approach to high-dimensional problems.
Real-World Posterior Distributions
The method is further validated on posterior-db targets, including the garch11 volatility model, the eight-schools hierarchical model, and Gaussian process regression. Each model presents unique challenges in terms of prior structure, parameter constraints, and posterior geometry. The PoE VI approach is shown to yield accurate variational approximations, with expert selection tailored to the complexity of each target.
Implementation Considerations and Trade-Offs
- Computational Requirements: The method is CPU-efficient and parallelizable, but the estimation of normalizing constants and importance sampling can become expensive with large numbers of experts or high-dimensional targets.
- Expert Selection: Sparse expert weighting improves sampling efficiency and fit quality; future work may focus on more principled expert selection algorithms beyond the current heuristic.
- Integrability Constraints: Careful enforcement of integrability is necessary, especially when inverse scale matrices are not positive definite.
- Scalability: The approach scales to and beyond, but sample size and batch size must be increased to maintain accuracy in high dimensions.
- Baseline Comparisons: The PoE VI method is competitive with normalizing flows and ADVI, particularly in non-Gaussian and multimodal settings.
Implications and Future Directions
The empirical results suggest that score-based VI with a PoE family is a flexible and robust approach for approximating complex posteriors. The use of Feynman parameterization for normalizing constant estimation and importance sampling is effective, but further improvements in expert selection and sampling efficiency are warranted. The method's scalability to high dimensions and challenging targets positions it as a promising alternative to flow-based and mean-field VI methods.
Future research may explore adaptive expert selection, integration with GPU-accelerated solvers, and extensions to hierarchical and structured models. Theoretical analysis of convergence rates and sample complexity in the presence of sparsity and anisotropy would further strengthen the practical utility of the approach.
Conclusion
The paper provides a thorough empirical and methodological investigation of score-based variational inference using a product of experts family. The approach demonstrates strong performance on synthetic and real-world targets, with robust estimation of normalizing constants and efficient sampling procedures. While challenges remain in expert selection and scalability, the method offers a compelling framework for flexible, high-dimensional variational inference, with clear avenues for future enhancement and application.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
Overview
This paper studies a way to build flexible probability models by multiplying together many simple “experts.” Think of each expert like a small flashlight that shines on a certain area where it thinks the data should be. When you multiply experts (a “Product of Experts,” or PoE), the overlap of their lights gets bright, and places where only one or two shine stay dim. This makes sharp, detailed shapes that can match complicated data.
The authors use this PoE idea inside a method called variational inference (VI), which is a way to make fast, approximate Bayesian analysis. In this appendix, they run careful experiments to check two practical pieces of the PoE-VI method:
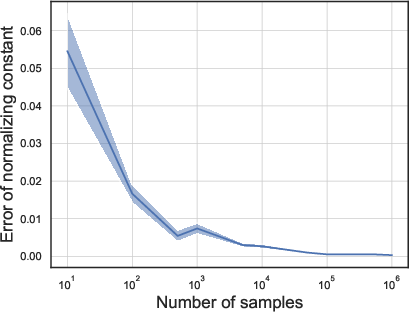
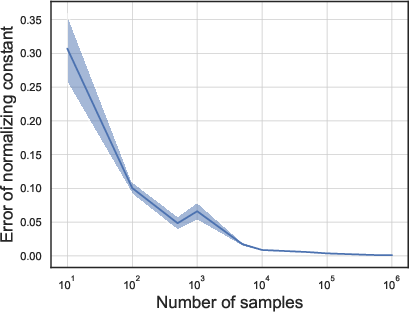
- How well they can estimate the “normalizing constant” (a scale factor that makes probabilities add up to 1).
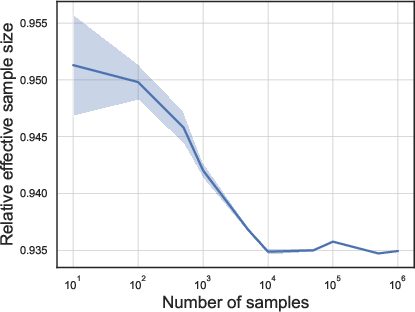
- How well their sampling method works (how efficient it is).
They also describe the target problems they test on, their training setup, and extra results.
Key questions the paper asks
- Can we accurately and efficiently estimate the normalizing constant for PoE models using a “Feynman parameterization” trick?
- How efficient is the importance sampling procedure used in PoE-VI? (In other words, how many useful samples do we really get?)
- How does PoE-VI behave on different kinds of target distributions, from simple mixtures to tricky, curved, or heavy‑tailed shapes?
- How does PoE-VI compare to standard variational baselines like Gaussian VI and normalizing flows under a fair computing budget?
How they studied it (methods in simple terms)
First, some quick translations of technical terms into everyday language:
- Product of Experts (PoE): Combine many simple “opinions” (experts) by multiplying them. The model is strongest where multiple experts agree.
- Normalizing constant: A scale factor that makes sure the total probability equals 1. Without it, you have the right shape but the wrong overall scale.
- Feynman parameterization: A math trick to rewrite a hard normalization integral into an average over simpler random “weights” assigned to experts.
- Importance sampling: A way to estimate an answer by drawing samples from an easier distribution and then reweighting them so the final estimate matches the target.
- Effective Sample Size (ESS): A score that tells you how many equally useful samples your weighted samples are worth. Closer to the total number of samples is better.
What they did:
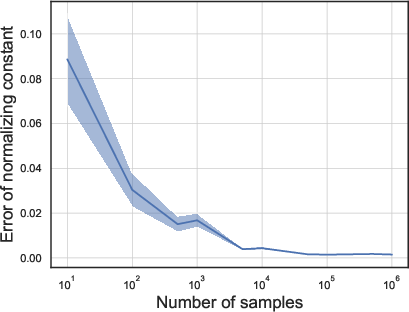
- Estimating the normalizing constant: They drew lots of random “weight vectors” that tell how much to trust each expert at a time, averaged the results, and compared estimates to a very accurate “ground truth” built from 5 million draws.
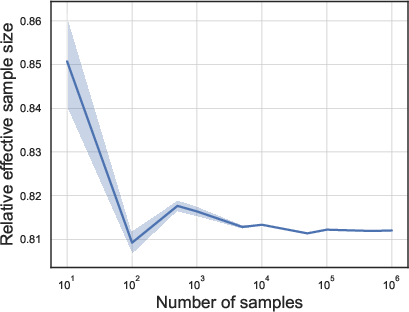
- Testing sampling efficiency: They ran importance sampling for different numbers of samples and computed the relative ESS (ESS divided by total samples). A relative ESS near 1 means very efficient sampling; smaller values mean less efficient.
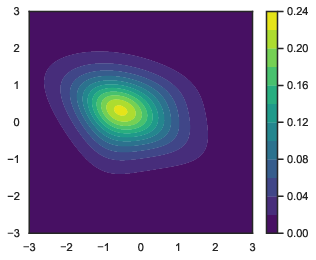
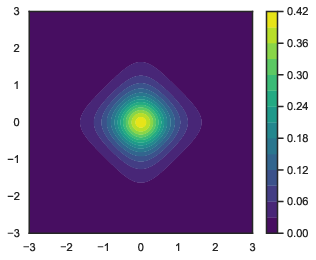
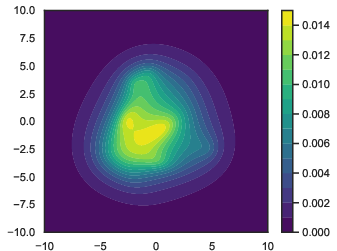
- Test problems: They tried three PoE examples designed to be challenging in different ways:
- Example 1: Skewed and heavy-tailed (the distribution leans to one side and has more extreme values).
- Example 2: Highly anisotropic (it’s very stretched in one direction and squished in another).
- Example 3: Many experts where only a few matter (sparse weights).
- Broader targets: They also tested on classic synthetic shapes (like a “banana”-shaped Rosenbrock, diamond, funnel, Gaussian mixtures, and skewed heavy-tailed sinh–arcsinh distributions) and real Bayesian models from the posterior-db library (like GARCH volatility, Eight Schools, and Gaussian process regression).
- Baselines and training: They compared to:
- Gaussian VI (ADVI): Approximates with a single bell curve.
- Normalizing flows: Start with a simple bell curve and “warp” it through neural networks to match complex shapes.
- They tuned learning rates fairly through small pilot runs, used the same number of gradient steps across methods, and ran everything on CPU.
Main findings and why they matter
Normalizing constant estimation:
- As they used more samples, the error in the normalizing constant estimate dropped, as expected. This says the Feynman parameterization–based estimator is reliable with enough samples.
Sampling efficiency (importance sampling):
- In Example 1 (skew + heavy tails) and Example 2 (high anisotropy), the relative ESS was high (above about 0.8). That means the sampling method was very efficient in these tough but structured cases.
- In Example 3 (many experts but most barely used), the relative ESS dropped to around 0.3–0.5. That means the sampling still works, but it’s less efficient—you need more samples to get the same quality.
Why this matters:
- High ESS means faster, more stable learning and evaluation in VI.
- The drop in ESS for the “many but sparse” expert case points to a practical limitation: if you place too many unhelpful experts, you waste sampling effort.
Other experimental notes:
- Despite the harder sampling in the sparse-expert case, the VI fits still gave accurate results when they used enough samples.
- The authors suggest two ways to improve: design samplers that exploit sparse weights and select a smaller, smarter set of experts rather than many with reweighting after the fact.
- On a range of synthetic and real problems, PoE-VI behaved well, and the setup ensured a fair comparison to standard baselines.
Implications and impact
- Practical takeaway: PoE-VI can model complex, real-world shapes effectively and can estimate its normalizing constant accurately with enough samples.
- Efficiency insight: Sampling is very efficient when experts are well-placed and not overly sparse. When many experts have near-zero weight, efficiency drops, which motivates better expert selection or specialized samplers.
- Future directions:
- Smarter expert selection to place fewer but more impactful experts.
- Samplers that take advantage of weight sparsity to boost ESS.
- Broader impact: Improving these parts of PoE-VI can make fast Bayesian inference more accurate and reliable on challenging problems, helping scientists and engineers analyze data without needing slow, heavy-duty sampling methods.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a concise list of unresolved issues identified in the paper that future work could address:
- Normalizing constant estimation:
- No theoretical analysis of bias, variance, or convergence rates of the Feynman-parameterization Monte Carlo estimator; unclear dimension- and K-dependence.
- Lack of comparison to alternative estimators (e.g., bridge sampling, annealed/tempered transitions, thermodynamic integration, path sampling, harmonic mean variants) to assess efficiency and robustness.
- No variance-reduction strategies explored (e.g., control variates, stratification over the Dirichlet simplex, Rao–Blackwellization, quasi–Monte Carlo).
- Unclear error control when the normalizing constant is estimated with finite samples (500k), yet used in forward-KL evaluations; no confidence intervals or error bars reported for log-normalizer estimates.
- Importance sampling procedure:
- The proposal family and its optimality conditions are not analyzed; no adaptive or sequential variants (e.g., adaptive IS, SMC, resampling) are considered.
- The effect of weight degeneracy (low relative ESS) on VI gradient quality and convergence is not quantified; no thresholds or adaptive batch-size policies based on ESS are provided.
- No paper of how ESS scales with D, K, anisotropy, or α-sparsity; Example 3 indicates degradation, but general conditions and remedies are not systematically explored.
- The sampling algorithm does not exploit α-sparsity; no specialized proposals, marginalization, or subspace sampling over active experts are developed.
- Integrability and model specification:
- Integrability conditions for general (possibly indefinite) inverse scale matrices Λk are not rigorously characterized; the paper falls back to a weaker constraint (2∑k αk > D) and post-hoc verification without formal guarantees.
- No diagnostic or algorithmic safeguard to ensure intermediate iterates during optimization remain integrable; unclear failure modes and corrections when constraints are violated.
- Sensitivity to the slack parameter ε=1e−12 is not explored; numerical stability and feasibility margins lack analysis.
- Expert selection and dictionary design:
- The heuristic expert placement (parameters M, s, β) lacks a principled selection criterion; no data-driven or optimization-based method to choose K, place experts, or curate a compact dictionary.
- No merging/pruning strategies or sparsity-inducing penalties to encourage a minimal active set; risk of redundancy and computational overhead for large K remains.
- No ablation or sensitivity analysis mapping the number of (active) experts to approximation error and computational cost; absence of guidelines for scaling with dimension and multimodality.
- Open question: can experts’ locations/scales be learned (jointly with α) under integrability constraints to reduce reliance on heuristic placement?
- Optimization and VI algorithm:
- The score-based VI reweighting uses fixed hyperparameters (λt=1, T=20, batch size B) without a systematic paper of convergence behavior, step-size schedules, or stopping criteria across targets.
- No analysis of gradient variance and its impact on convergence; lack of variance-reduction methods (e.g., control variates, antithetic sampling) for the stochastic objectives.
- The quadratic program’s scalability and robustness with respect to K, D, and constraint tightness are unreported; solver convergence diagnostics, sensitivity to conditioning, and GPU viability are not examined.
- Theoretical guarantees for convergence of the overall algorithm in the nonconvex setting (with Monte Carlo noise) are not provided; practical conditions for success/failure are unclear.
- Expressiveness and approximation properties of PoE:
- No theoretical approximation guarantees (e.g., rates, covering numbers) relating K and expert shapes to target complexity (multimodality, skewness, heavy tails).
- Tail behavior control is not analyzed; risk of under/over-concentration intrinsic to PoE is not quantified, especially on funnel-like or heavy-tailed targets.
- Interaction between target-space transformations (via BridgeStan) and PoE expressiveness in the transformed space is not studied; guidelines for choosing or composing transformations are absent.
- Evaluation methodology:
- Reliance on a large “ground-truth” MC run (5M samples) to benchmark the normalizer is impractical for real problems; no surrogate diagnostics proposed for routine use.
- Limited metrics (ESS, forward KL) without calibration/coverage checks or posterior predictive assessments; lack of comprehensive diagnostics when ground truth is unavailable.
- Baseline fairness: learning-rate grid search but no wall-clock or memory comparisons; equal score evaluations may not reflect actual computational cost parity across methods.
- Scalability and compute:
- Experiments run on large-memory CPU hardware; no analysis of memory footprint, parallelization, or GPU acceleration for the QP, sampling, and determinant computations with growing K and D.
- The cost of evaluating determinants and other matrix operations in the Feynman-based estimator is not profiled; numerical stability for highly anisotropic or ill-conditioned Λ(w) is unexamined.
- Reproducibility and specification:
- The importance-sampling proposal for PoE (referenced eq. importance-samples) is not fully specified in the appendix, limiting exact reproducibility of the sampling/VI pipeline.
- Hyperparameter defaults (K, M, s, β, B, T) lack principled tuning rules; no automated selection strategy or sensitivity mapping to target properties is provided.
- Open algorithmic directions suggested but not developed:
- Design of sparsity-aware samplers for α-sparse regimes and principled expert selection beyond the current heuristic.
- Adaptive sampling schedules driven by ESS or gradient-noise estimates.
- Methods to learn expert parameters (locations, scales) end-to-end under integrability constraints.
- Hybrid estimators for the normalizer combining Feynman parameterization with bridging/AIS or RQMC for improved efficiency.
Practical Applications
Immediate Applications
The following applications can be deployed with the methods and findings reported in the paper, given access to the target’s log-density and score (gradient), and the ability to transform constrained parameters to an unconstrained space (e.g., via BridgeStan).
- Robust variational inference for non-Gaussian posteriors in probabilistic programming (software, academia, industry)
- Use case: Replace or complement ADVI/normalizing flows with PoE-VI on targets that are multimodal, skewed, heavy-tailed, or anisotropic (e.g., funnel, Rosenbrock, sinh–arcsinh).
- Tools/workflows: BridgeStan to expose density/gradient; Python PoE-VI implementation with OSQP via jaxopt_osqp; batch-size and learning-rate settings as in the experiments; monitor ESS during importance sampling.
- Assumptions/dependencies: Requires access to log p and ∇ log p; integrability constraints (e.g., 2∑αk > D with verification); adequate sample sizes for normalizing constants and importance weights (often ≥ 500k for forward KL estimates).
- Fast approximate inference for time-series volatility (finance)
- Use case: Apply PoE-VI to GARCH(1,1)-type models to obtain approximate posterior summaries for volatility and risk metrics (e.g., VaR/ES) under heavy-tailed noise and parameter constraints.
- Tools/workflows: BridgeStan for model transformation; PoE-VI runs with K≈100 experts and QP reweighting; ESS tracking to assess sampling efficiency.
- Assumptions/dependencies: Accuracy depends on quality of expert placement and reweighting; data-generating process consistent with model assumptions; may require larger B for reliable tail estimates.
- Hierarchical modeling with partial pooling (education, healthcare, social science, academia)
- Use case: Eight-schools-style models (and analogs in hospitals, classrooms, clinics) where PoE-VI can deliver fast approximate posteriors for group effects and hyperparameters (μ, τ) in settings known to challenge Gaussian VI.
- Tools/workflows: PoE-VI with 50–100 experts; BridgeStan transformations; ESS monitoring to ensure effective posterior sampling; comparison against ADVI/flows.
- Assumptions/dependencies: Proper reparameterization to unconstrained space; heavy tails/hyperpriors compatible with PoE family; adequate number of experts for multimodal or skewed structures.
- Gaussian process regression hyperparameter inference (software, ML, engineering)
- Use case: Quick approximate posteriors for GP hyperparameters (ρ, α, σ) to support model selection and predictive uncertainty when full MCMC is too costly.
- Tools/workflows: PoE-VI with ~70 experts; importance sampling for posterior summaries; cross-validation or marginal likelihood proxies using estimated normalizing constants.
- Assumptions/dependencies: Covariance structure fit for log-likelihood gradients; stability of Gram matrix operations; sufficient sampling budget for reliable KL estimates.
- Approximate normalizing constant estimation for product-of-experts models (software, energy-based modeling, academia)
- Use case: Use Feynman parameterization with Monte Carlo sampling to estimate partition functions/normalizing constants of PoE densities for model comparison or calibration.
- Tools/workflows: Dirichlet-weight sampling; error benchmarking against high-sample “ground truth”; relative ESS as a quality metric.
- Assumptions/dependencies: Variance control via sufficient B; accuracy sensitive to sparsity patterns in α and anisotropy; numerical stability when Λ matrices are ill-conditioned.
- Sampling quality diagnostics via relative ESS (software, academia, industry)
- Use case: Integrate relative ESS monitoring into VI pipelines to adapt sample counts B and detect when expert sparsity or anisotropy degrades importance sampling efficiency.
- Tools/workflows: Compute relative ESS = ESS/B from normalized importance weights; adjust B adaptively; log diagnostics alongside loss/ELBO curves.
- Assumptions/dependencies: Stable weight normalization; representative proposal distribution; consistent seeds for repeatability.
- Resource-constrained inference on CPUs (software, industry, academia)
- Use case: Run PoE-VI on CPU-only systems for moderate-dimensional problems (≤50D) when GPU accelerators are unavailable, using the paper’s demonstrated settings.
- Tools/workflows: Adopt batch sizes and iteration counts from the experimental setup; OSQP-based QP solver; learning-rate grids for baselines (ADVI/flows) as demonstrated.
- Assumptions/dependencies: Memory sufficient for large B (up to millions of samples for some targets); careful tuning when targets are highly non-Gaussian or high-dimensional.
Long-Term Applications
These opportunities require further research, scaling, or development to reach production-level maturity.
- Sparse-aware importance sampling for PoE with many experts (software, academia)
- Opportunity: Design samplers tailored to sparse α weight vectors to boost relative ESS from ~0.3–0.5 to ≥0.8 when many experts exist but few are active.
- Potential products/workflows: “Sparse-Dirichlet” proposal distributions; adaptive resampling strategies; variance reduction techniques.
- Assumptions/dependencies: Algorithmic modifications to leverage sparsity; theoretical analysis of variance and bias under sparse proposals.
- Automated expert selection and placement beyond heuristics (software, robotics, academia)
- Opportunity: Replace heuristic “place-many-then-reweight” strategy with data-driven expert placement (active learning, clustering, score-matching) to reduce K while preserving fit.
- Potential products/workflows: AutoPoE modules that propose experts based on posterior geometry (gradients, Hessian proxies, score dispersion); curriculum learning to add experts progressively.
- Assumptions/dependencies: Robust criteria for expert addition/removal; convergence guarantees under adaptive expert sets; compatibility with QP constraints.
- Scaling PoE-VI to high dimensions and large datasets (software, industry)
- Opportunity: Extend to hundreds/thousands of parameters via GPU acceleration, structured experts (low-rank Λ, block-diagonal designs), and stochastic approximations of normalizing constants.
- Potential products/workflows: GPU-accelerated QP solvers; distributed importance sampling; structured PoE libraries for hierarchical and deep models.
- Assumptions/dependencies: Numerical stability in high dimensions; control of variance for importance weights; memory management for very large B.
- Native integration with probabilistic programming languages (software, academia)
- Opportunity: Offer PoE-VI as a built-in VI engine in Stan, PyMC, NumPyro, TFP, with automatic unconstraining and score access via language APIs.
- Potential products/workflows: PPL plugin packages; unified diagnostic suite (ESS, KL, integrability checks); auto-tuning of batch sizes and learning rates based on pilot runs.
- Assumptions/dependencies: Standardized access to gradients; efficient bridging to unconstrained space; consistent constraint handling and integrability verification.
- Sensor fusion via product-of-experts with learned experts (robotics, autonomous systems)
- Opportunity: Use PoE formulations to fuse heterogeneous sensor streams (vision, lidar, IMU) with learned expert components; apply PoE-VI for uncertainty calibration in perception stacks.
- Potential products/workflows: Modular sensor expert libraries; online reweighting for changing sensor reliability; ESS-driven monitoring to detect degraded fusion.
- Assumptions/dependencies: Mapping sensor likelihoods to differentiable log-densities; real-time constraints; robust handling of anisotropy and skew in sensor noise.
- Heavy-tailed and multimodal risk modeling for policy and enterprise analytics (policy, finance, energy)
- Opportunity: Rapid scenario analysis of extreme events (market shocks, demand spikes) using PoE-VI to approximate posteriors where tails matter and standard VI underfits.
- Potential products/workflows: Tail-focused PoE configurations; policy dashboards with ESS and KL diagnostics; hybrid VI–MCMC workflows where PoE provides warm-starts.
- Assumptions/dependencies: Validity of heavy-tailed priors/likelihoods; careful calibration of experts to reflect domain-specific tail behavior; governance for model risk.
- Teaching, benchmarking, and method development on challenging targets (academia, education)
- Opportunity: Use the paper’s synthetic targets (funnel, Rosenbrock, sinh–arcsinh) to benchmark new VI/MCMC algorithms and teach inference under pathological geometries.
- Potential products/workflows: Open benchmark suites with reproducible settings; standardized reporting (ESS, normalizing constant errors, KL metrics); curriculum materials.
- Assumptions/dependencies: Community adoption of targets and metrics; consistent computational budgets across methods for fair comparison.
Glossary
- Adam: A stochastic gradient-based optimizer that adapts per-parameter learning rates using estimates of first and second moments of gradients. "using Adam"
- ADVI: Automatic Differentiation Variational Inference; a VI method that uses autodiff and stochastic optimization to maximize the ELBO. "ADVI"
- Anisotropy: Direction-dependent scaling or variability in a distribution, often implying different variances along different axes. "High anisotropy."
- BaM: A baseline stochastic optimization method referenced by the authors for comparison in experiments. "For BaM, the learning rate schedule was fixed to"
- BlackJAX: A JAX-based library providing Bayesian sampling algorithms such as HMC. "blackjax"
- BridgeStan: A library that provides direct access to Stan models’ log densities and gradients via stable language bindings. "BridgeStan library"
- Coupling layer: A building block of normalizing flows that applies invertible transformations to a partition of variables while keeping the rest unchanged. "coupling layer"
- Dirichlet distribution: A distribution over probability simplex vectors, commonly used as a prior for categorical probabilities. "Dir(\alpha)"
- ELBO: Evidence Lower Bound; the objective function maximized in variational inference to approximate the posterior. "the ELBO"
- Effective sample size (ESS): A diagnostic that quantifies the equivalent number of independent samples after accounting for weight variability in importance sampling. "effective sample size (ESS)"
- eight-schools: A canonical hierarchical Bayesian model involving school-specific effects with shared hyperparameters. "eight-schools."
- Feynman parameterization: A technique introducing auxiliary parameters to simplify integrals of products, used here to estimate a normalizing constant. "Feynman parameterization"
- FlowMC: A software package implementing flow-based methods for Monte Carlo and variational inference. "FlowMC"
- Forward KL divergence: The Kullback–Leibler divergence KL(p||q) measuring how the approximation q diverges from the target p. "forward KL divergence"
- Funnel target: A challenging hierarchical distribution exhibiting a funnel-shaped geometry due to scale parameters. "Funnel target"
- garch11: The GARCH(1,1) volatility model used as a posterior-db target in the experiments. "garch11."
- Gaussian process regression: A Bayesian nonparametric regression framework using a GP prior over functions. "Gaussian process regression"
- Gamma distribution: A continuous distribution parameterized by shape and rate (or scale), used for positive-valued variables. "gamma(25, 4)"
- gp-regr: A posterior-db benchmark referring to Gaussian process regression. "gp-regr."
- Gram matrix: The matrix of pairwise kernel evaluations among data points used in GP models. "gram matrix"
- Hamiltonian Monte Carlo (HMC): An MCMC method leveraging Hamiltonian dynamics to explore probability distributions efficiently. "HMC"
- Importance sampling: A Monte Carlo technique that estimates expectations by reweighting samples drawn from a proposal distribution. "importance sampling procedure"
- Integrability: The property that a proposed density integrates to one; constraints ensure the resulting PoE density is normalizable. "integrability"
- Inverse scale matrix: The precision matrix (inverse covariance) parameterizing elliptical expert factors in the PoE. "inverse scale matrices"
- JAX: A high-performance autodiff and XLA-accelerated numerical computing framework. "JAX wrapper"
- jaxopt_osqp: A JAX-based wrapper around the OSQP solver for quadratic programming. "jaxopt_osqp"
- Monte Carlo estimate: An estimate computed via random sampling, typically to approximate integrals or expectations. "a Monte Carlo estimate"
- Normalizing constant: Also known as the partition function; ensures the unnormalized density integrates to one. "normalizing constant"
- Normalizing flow: A family of models that transform simple base distributions into complex ones via invertible mappings. "normalizing flow"
- OSQP: Operator Splitting Quadratic Program; a solver for convex quadratic programs. "OSQP solver"
- PoE (Product of Experts): A model family that multiplies expert densities to form a sharper composite distribution. "PoE densities"
- Quadratic program: An optimization problem with a quadratic objective and linear constraints. "quadratic program"
- Quadrature: Numerical integration methods used to compute integrals (e.g., normalizing constants). "quadrature"
- RealNVP: A specific normalizing flow architecture (Real-valued Non-Volume Preserving) using affine coupling layers. "realNVP"
- Relative ESS: The ESS normalized by the total number of samples, indicating sampling efficiency. "relative ESS"
- Rosenbrock: A nonconvex, “banana-shaped” test function/distribution used to assess optimization and sampling methods. "Rosenbrock"
- Score (of the target): The gradient of the log-density, ∇ log p(z), used in gradient-based fitting and diagnostics. "score of the target"
- Score-based VI method: A variational inference approach that leverages the target’s score function during optimization. "score-based VI method"
- sinh-arcsinh distribution: A flexible distribution achieving skewness and heavy tails via the sinh–arcsinh transform. "sinh-arcsinh"
- Standard error: The estimated standard deviation of a sampling-based estimator (e.g., of a mean). "standard error"
- Truncated-normal distribution: A normal distribution restricted to a subset of its support (e.g., positive reals). "truncated-normal"
- Variational family: The parameterized set of candidate distributions over which VI optimizes. "variational family"
- Variational Inference (VI): An optimization-based approach to approximate posterior distributions. "VI"
Collections
Sign up for free to add this paper to one or more collections.