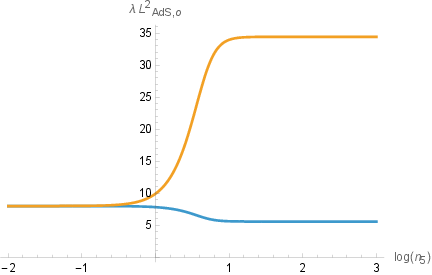O(16)$\times$O(16) heterotic theory on $AdS_3\times S^3\times T^4$ (2510.20915v1)
Abstract: In this paper, we study non-supersymmetric $O(16)\times O(16)$ heterotic theory on an $AdS_{3}\times S{3}\times T{4}$ background, finding a family of vacua parameterized by a pair of flux integers. Adding the one-loop scalar potential to the effective theory contributes positively to the cosmological constant, but we find that there is no uplift to de Sitter for any values of the fluxes. We study the fluctuations around these vacua and show that all scalar and tensor modes from the six-dimensional effective theory lie above the Breitenlohner-Freedman bound. The moduli coming from the torus compactification will also be above the bound, at least for a large range of fluxes.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
Overview
This paper explores a version of string theory called the O(16)×O(16) heterotic string when the universe’s shape is split into three parts: AdS₃ (a space with negative curvature, like a saddle), S³ (a 3D sphere), and T⁴ (a 4D donut-like shape called a torus). The authors look for “vacua,” which are stable, low-energy states of the theory, and ask whether quantum effects can change these states into de Sitter (positively curved, balloon-like) universes. They also test whether small vibrations around these vacua are stable.
To make things more accessible, here are a few key terms in everyday language:
- AdS (Anti-de Sitter): a space that curves inward like a saddle.
- de Sitter: a space that curves outward like a balloon; often used to model an expanding universe.
- Flux integers: whole numbers that count how many times certain invisible “fields” wrap around holes in the shapes S³ and T⁴, like rubber bands around a donut.
- One-loop correction: a small quantum tweak to the energy from particles briefly popping in and out of existence.
- BF bound: a safety limit in AdS spaces; some “negative mass” modes can still be stable, but only if they aren’t too negative.
- Moduli: adjustable settings that control the size and shape of extra dimensions (like sliders you can move).
- Tachyon: a sign of instability in a theory; if present, it means the state wants to “roll away” and isn’t stable.
Goals and Questions
The paper asks:
- Can this non-supersymmetric heterotic string theory on AdS₃×S³×T⁴ produce stable vacuum states?
- If we include quantum corrections (one-loop effects), can we “uplift” an AdS vacuum (negative energy) into a de Sitter vacuum (positive energy)?
- Are small vibrations (fluctuations) around these vacua stable, especially the moduli that come from the torus T⁴? Do any go below the BF bound?
Methods and Approach
Think of the setup like building a model universe with LEGO blocks:
- The blocks are shapes: AdS₃, S³, T⁴.
- The rubber bands (flux integers n₁ and n₅) wrap around some of these blocks to keep things in place.
- The energy of this universe comes from two sources:
- Tree-level energy: the basic, classical energy, before quantum effects.
- One-loop energy: small quantum corrections added later.
Here’s how they studied it:
They wrote down the “potential” (energy function) at tree-level using the sizes of S³ and T⁴ and the flux numbers. Then they found the point where this potential is minimized (a vacuum).
They added the one-loop quantum correction to the potential. This correction is computed using a partition function (a tool that counts all possible ways strings can vibrate) integrated over shapes of the torus. In simple terms, it’s like adding a small, carefully calculated wiggle to the energy landscape.
They analyzed small vibrations around the vacuum by expanding fields (like the metric and the B-field) in spherical harmonics on S³. Spherical harmonics are like the musical notes that fit perfectly on a sphere; each note tells you how a particular kind of vibration behaves.
They computed effective masses for these vibrations and checked the BF bound to see if any modes are unstable.
Main Findings
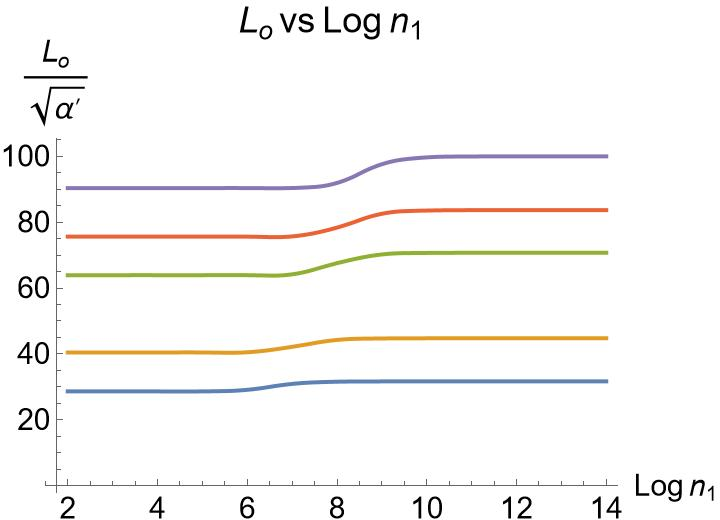
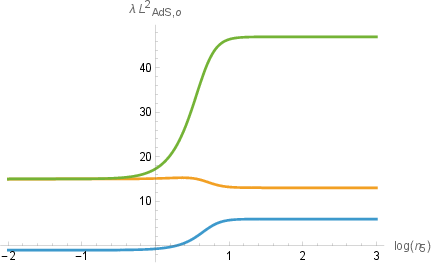
There is a whole family of AdS₃×S³×T⁴ vacua, labeled by two flux integers n₁ (electric-type) and n₅ (magnetic-type).
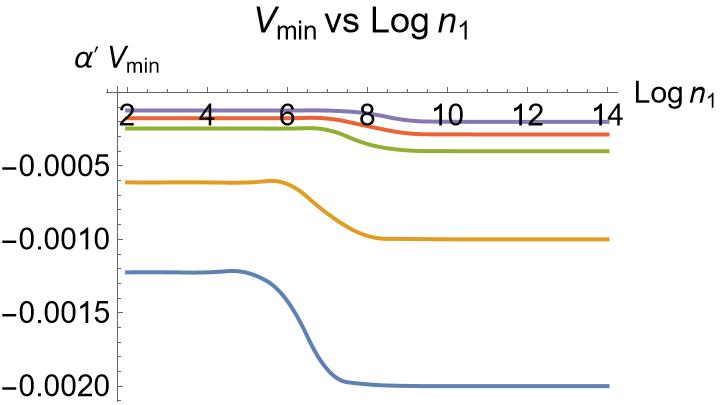
The one-loop quantum correction raises the energy (it contributes positively to the cosmological constant), but it never raises it enough to become de Sitter. In other words, no uplift to a positive-energy, expanding de Sitter universe occurs in this setup.
When checking stability:
- All the “six-dimensional” scalar and tensor modes (coming from the effective gravity theory) stay above the BF bound. That means no tachyons from these modes; they are stable.
- The moduli from the T⁴ compactification (the shape and size settings of the torus) are mostly safe: for a large range of flux choices, they also stay above the BF bound. However, in the special limit where n₁ goes to zero (turning off the electric-type flux), some torus moduli can slip below the BF bound. That indicates a likely instability right at that extreme.
- The authors also identify “intrinsically quantum” vacua: in the n₁=0 limit, the one-loop correction prevents a blow-up of the string coupling and keeps the system finite. But precisely there, some moduli tend to become unstable.
Why This Matters
- Many researchers hope string theory can produce realistic universes with positive cosmological constant (de Sitter), matching our observed accelerated expansion. This paper adds evidence that, at least in this specific non-supersymmetric heterotic setup on AdS₃×S³×T⁴, such de Sitter vacua do not arise—even after quantum corrections.
- It maps part of the “landscape” of possible string vacua, showing where stable AdS solutions exist and where instabilities appear, especially for moduli.
- It shows that non-supersymmetric AdS vacua can be remarkably stable against many kinds of small vibrations, which is scientifically interesting because non-supersymmetric models are often harder to control.
- The work guides future searches: if de Sitter uplift is needed, it likely requires different ingredients (other compactifications, fluxes, or corrections). And it points out where potential instabilities (like torus moduli below the BF bound) can show up, helping researchers avoid problematic regions.
Simple Takeaway
Imagine trying to balance a ball in a bowl (finding a stable vacuum in string theory). The authors found bowls shaped by two wrapping numbers (fluxes). Adding a small quantum “nudge” lifts the ball a bit but never flips the bowl into a hill (de Sitter). Most small wiggles of the ball are safe and don’t grow out of control, meaning the bowl is stable. However, if you turn off one of the wraps completely, the bowl gets too shallow in some directions, and the ball can roll away—that’s instability. Overall, this setup is stable in many cases but cannot produce the kind of expanding universe we see today.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a single, consolidated list of what remains missing, uncertain, or unexplored in the paper. Each item is phrased to enable concrete follow-up by future researchers.
- Regime of validity of the one-loop approximation: quantify when neglecting two-loop and higher-genus/worldsheet corrections is justified, especially in the large-s limit (small |n₁|) where corrections to both the vacuum energy and masses could be significant.
- Impact of higher-derivative (α′) corrections: compute curvature and torsionful-connection corrections to the 10D/6D effective action and to the scalar potential; assess their effect on the AdS cosmological constant and stability.
- Flat-background approximation for the one-loop vacuum energy: replace the R¹,⁵×T⁴ approximation by a controlled calculation on AdS₃×S³×T⁴ (e.g., via heat-kernel/Schwinger–DeWitt techniques) and bound the error as a function of L/√α′.
- Full Hessian of the Narain moduli potential: compute the complete 80×80 Hessian (μ_{αβ}) of the integrated genus-one partition function at the square self-dual torus and at other critical points; provide eigenvalues and eigenvectors to determine the precise spectrum and identify directions that cross the BF bound.
- Map of stability region in flux space: determine the exact range of fluxes (n₁, n₅) for which all Narain moduli stay above the BF bound; locate thresholds (maximum s or minimum |n₁| at fixed |n₅|) beyond which instabilities develop.
- “Knife-edge” directions: identify and classify knife-edge solutions in the T⁴ moduli space and quantify their stability properties under flux variations and loop corrections.
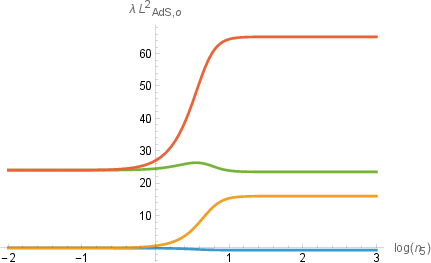
- General dependence of λ on moduli: compute λ (the integrated genus-one partition function) and the associated μ_{αβ} across representative loci in the Narain moduli space beyond the square self-dual torus; determine whether conclusions (e.g., no dS uplift) persist at other critical points.
- Vector-mode stability: perform a full analysis of the coupled vector modes S_μ{(ℓ,±1)} and C_μ{(ℓ,±1)} (including residual gauge fixing), extract their AdS₃ masses, and check for BF-like instabilities or ghost modes.
- Role of the heterotic Bianchi identity: incorporate the torsionful-spin-connection and gauge Chern–Simons terms (dH = α′(Tr R∧R − Tr F∧F)); check consistency of the background (including AdS₃×S³ curvature) with anomaly cancellation and flux quantization, and determine induced corrections to the potential.
- Gauge bundles and fluxes on T⁴: explore turning on gauge bundles, gauge fluxes, and nontrivial Wilson lines; analyze how they modify λ, the moduli masses, and the prospects for stability or uplift.
- Nonperturbative instabilities: assess potential decay channels (bubble-of-nothing on T⁴ cycles, NS5-brane nucleation changing n₁/n₅, Euclidean instantons, AdS₃ long-string instabilities), estimate decay rates, and determine the lifetime of the AdS vacua.
- Prospects for de Sitter uplift with additional ingredients: test whether adding localized sources, different flux sectors, orbifolds of T⁴, KK monopoles, or controlled α′/loop corrections can yield a stable dS vacuum without reintroducing tachyons.
- Worldsheet CFT completeness: construct and analyze the exact heterotic worldsheet CFT for AdS₃×S³ with NS flux and T⁴ (levels k vs. fluxes, modular invariance, absence of tachyons), and compare exact CFT data directly to the effective potential and mass spectrum.
- 10D backreaction and warping: determine whether loop-induced vacuum energy and mass terms backreact nontrivially on the 10D geometry and dilaton profile (beyond constant φ, product metric); compute the corrected background and re-evaluate stability.
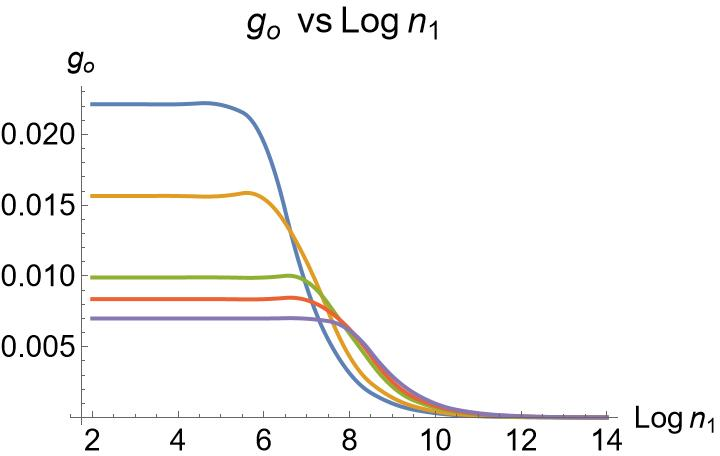
- Threshold corrections to g_s and moduli dependence: verify whether the combination g_o²/v remains moduli-independent beyond one loop; include threshold corrections to gauge couplings and their backreaction on flux quantization and the potential.
- Fermionic sector and anomalies: analyze the spectrum of fermions (and possible anomalies) in the non-supersymmetric O(16)×O(16) background on AdS₃×S³×T⁴; check for fermionic instabilities or anomaly-induced constraints.
- Full KK towers: extend the stability analysis beyond scalars and tensors to complete Kaluza–Klein towers (including spinors and vectors) to ensure that no higher modes breach the BF bound or introduce pathologies.
- Precise treatment of intrinsically quantum solutions: characterize the n₁→0 (large-s) branch quantitatively (including μ_{αβ} eigenvalues), determine which moduli become unstable, and explore possible endpoints or alternative vacua.
- Robustness of the “no dS uplift” conclusion: test whether the negative three-dimensional cosmological constant persists when including higher loops, α′ corrections, or alternative moduli points; attempt a general no-go or identify counterexamples.
- Holographic data: extract AdS₃/CFT₂ quantities (central charge, operator dimensions for bulk modes) for the constructed vacua; use the dual CFT to cross-check stability and the presence/absence of pathologies (e.g., accumulation of light states).
- Dependence on T⁴ volume and shape: analyze how varying v away from (2π)⁴ and moving in shape moduli space affects λ, g_o, L_o, and the BF safety margin; identify regions where stability improves or worsens.
- Flux quantization under corrections: verify that electric/magnetic H₃ quantization conditions (and their relation to L and g_s) remain intact when loop and α′ corrections are included; determine any shifts or renormalizations.
- Dynamical evolution of instabilities: if some moduli cross the BF bound, model the time evolution in AdS₃, identify the new vacuum or runaway direction, and characterize the transition (barrier heights, tunneling rates).
- Generalization to other non-supersymmetric string models: repeat the analysis for the USp(32) Sugimoto and U(32) models on AdS₃×S³×T⁴; compare whether stability/no-uplift conclusions are model-dependent or universal.
Practical Applications
Immediate Applications
The following items can be deployed now by leveraging the paper’s analytical results, computational recipes, and negative/positive findings on stability and de Sitter uplift.
- AdS vacuum stability toolkit for string compactifications (sector: academia, software)
- Use case: Implement a reproducible pipeline to test non-supersymmetric AdS backgrounds for perturbative stability via the Breitenlohner–Freedman (BF) bound.
- Workflow:
- 1) Construct 6D effective actions with one-loop cosmological constant and moduli masses,
- 2) Impose flux quantization conditions and parameterize solutions in terms of flux integers n₁, n₅ and the dimensionless scale s = λ n₅² / |n₁|,
- 3) Expand fluctuations in S³ spherical harmonics,
- 4) Assemble and diagonalize mass matrices,
- 5) Automatically check BF bounds and identify potential instabilities in moduli directions.
- Tools: Mathematica/Maple/SymPy; numerical eigenvalue solvers (ARPACK, LAPACK); modular-integration routines for genus-one partition functions.
- Assumptions/dependencies: Validity of the large-radius approximation (AdS₃ × S³ much larger than T⁴); one-loop dominance (two-loop effects neglected); worldsheet supersymmetry with broken spacetime SUSY; accurate evaluation of λ from the torus partition function.
- Flux–stability dashboard for AdS₃ × S³ × T⁴ heterotic vacua (sector: academia, software)
- Use case: Rapid assessment of how stability and coupling respond to flux choices using the paper’s closed-form expansions and numerical strategies.
- Workflow: Inputs (n₁, n₅, torus volume v, λ) → outputs (g₀, L₀, Λ₃,o, stability flags for six-dimensional modes and torus moduli).
- Tools: A lightweight Python web service with plots akin to the paper’s Figure outputs; pre-coded small-s and large-s expansions; automated BF bound checks.
- Assumptions/dependencies: λ treated as an O(1) constant (e.g., λ ≈ 1.565 for the self-dual square torus); smooth behavior across flux ranges; numerical precision in modular integrals.
- Reference benchmark for modular integrals and Narain lattice computations (sector: academia, software)
- Use case: Use the computed λ and demonstrated critical points (self-dual square T⁴) as test data to validate new symbolic/numeric libraries handling modular forms, partition functions, and lattice sums in string compactifications.
- Tools: Test suites for Z(τ) integration over the fundamental domain; verification of vanishing first derivatives of Z(τ;ϕ) at critical points; Hessian estimation templates.
- Assumptions/dependencies: Accurate implementation of the genus-one partition function for the O(16)×O(16) heterotic theory; careful treatment of moduli dependence through Z(τ;ϕ) rather than via g₀²/v.
- Curriculum modules and problem sets for advanced courses (sector: education)
- Use case: Graduate-level teaching materials on non-supersymmetric string compactifications, BF bound analysis, AdS₃ × S³ harmonic expansions, and moduli stabilization with one-loop corrections.
- Tools: Annotated derivations of the effective potential; guided exercises on deriving mass matrices and checking BF bounds; computational labs implementing the expansions in s.
- Assumptions/dependencies: Students equipped with background in QFT, GR, and string CFT; access to CAS/HPC resources for numerical parts.
- Research direction filter: de Sitter no-go in this setup (sector: academia, research management)
- Use case: Inform project prioritization by noting that one-loop uplift to de Sitter does not occur for O(16)×O(16) on AdS₃ × S³ × T⁴; reallocate effort toward AdS stability, alternative compactifications, or different mechanisms for positive cosmological constant.
- Tools: Literature review synthesis; decision frameworks for theoretical exploration (e.g., focusing on AdS/CFT-compatible constructions).
- Assumptions/dependencies: Treating the no-uplift result as robust within the one-loop approximation and stated limits; openness to alternative corners of the string landscape.
Long-Term Applications
These applications require further research, scaling, validation of broader classes of compactifications, or development of dedicated tools/products.
- Automated “Vacuum Explorer” for non-supersymmetric landscapes (sector: academia, software, HPC)
- Use case: Large-scale scanning of flux choices and Narain moduli to locate critical points, compute λ, Hessians, and BF-bound-safe regions (including detection of “knife-edge” instabilities), across families of T⁴ (and beyond) compactifications.
- Product: A cloud-based platform integrating symbolic worldsheet CFT modules, modular integrals, and stability solvers with interactive visualization.
- Assumptions/dependencies: Scalable and accurate computation of Z(τ;ϕ) for broad moduli; inclusion of higher-loop corrections when s is not small; robust characterization of intrinsically quantum vacua.
- Cross-pollination with AdS₃/CFT₂ modeling of strongly coupled systems (sector: academia, condensed matter theory)
- Use case: Leverage evidence of perturbatively stable non-supersymmetric AdS₃ vacua (over ranges of fluxes) to refine candidate dual CFT₂ models and explore non-supersymmetric phases relevant to low-dimensional strongly correlated materials.
- Tools: Holographic modeling pipelines; match bulk spectra to boundary operator dimensions; paper how one-loop bulk corrections reflect in boundary data.
- Assumptions/dependencies: Valid AdS/CFT mapping for non-supersymmetric setups; identification of boundary theories with phenomenological relevance; careful interpretation of bulk instabilities vs. boundary RG flows.
- Narain lattice and modular integral libraries with cryptography/number theory links (sector: software, cryptography, computational mathematics)
- Use case: Enhanced numerical/symbolic libraries for modular forms and lattice sums may find secondary use in cryptographic primitives or modular-form-based algorithms, building on the paper’s integrational strategies over the modular fundamental domain.
- Tools: High-precision modular-integration engines; lattice-based optimizers; APIs for modular and automorphic form computations.
- Assumptions/dependencies: Demonstrable performance benefits vs. specialized number-theory libraries; rigorous security analyses if used in cryptography; careful abstraction from string-theoretic specifics.
- Machine-learning augmented stability prediction in moduli spaces (sector: software, academia)
- Use case: Train ML models on synthetic datasets produced by scanning (n₁, n₅, v, λ) and moduli to predict stability windows, BF-bound violations, and candidate minima without full analytic diagonalization.
- Product: “BF-Bound Predictor” assisting researchers to triage promising vacua before expensive computations.
- Assumptions/dependencies: Availability of reliable labeled datasets; generalization beyond the specific AdS₃ × S³ × T⁴ case; interpretability of model predictions for scientific use.
- Holography-inspired error-correcting codes and information architectures (sector: software, quantum information)
- Use case: Explore whether stable non-supersymmetric AdS₃ constructions can inform the design of robust holographic codes (e.g., tensor-network inspired), where bulk stability features guide code architecture.
- Tools: Translational frameworks from bulk mass spectra to code distance/robustness metrics; simulations of code behavior under perturbations inspired by BF-bound analogues.
- Assumptions/dependencies: Practical mapping from gravity-side features to code performance; community validation that non-supersymmetric holographic insights yield tangible benefits.
- Evidence-informed research policy for string cosmology claims (sector: policy, research governance)
- Use case: Use cumulative no-uplift and stability findings (including this paper) to advise funding bodies and collaborative networks on realistic milestones for de Sitter constructions in string theory; encourage standardized benchmarks and reproducibility.
- Tools: Policy briefs; agreed-upon computational benchmarks (e.g., λ values, flux ranges, stability matrices) for proposals claiming de Sitter uplift.
- Assumptions/dependencies: Continued aggregation of results across models; recognition that one-loop approximations and specific backgrounds constrain generality; responsiveness of governance structures to technical evidence.
Notes across all applications:
- Key dependencies include one-loop dominance, large-radius approximations, accurate modular integral evaluation, and the flux-controlled dimensionless parameter s. Where stability hinges on torus moduli Hessians, knife-edge directions and higher-loop corrections may alter feasibility.
Glossary
- AdS3: Three-dimensional Anti-de Sitter space, a maximally symmetric spacetime with constant negative curvature used in string theory backgrounds. "on an background"
- B-field: The antisymmetric two-form gauge field in string theory whose field strength is the three-form H3. "reducing the metric and -field on "
- Breitenlohner-Freedman bound: The stability bound for scalar masses in AdS spacetime; scalars with above this negative threshold are perturbatively stable. "lie above the Breitenlohner-Freedman bound"
- Cosmological constant: The vacuum energy density that sources spacetime curvature; positive values correspond to de Sitter, negative to Anti-de Sitter. "The six-dimensional cosmological constant for compactifications on is given as follows"
- Donder-Lorentz gauge: A gauge-fixing condition combining de Donder (harmonic) gauge for gravity and Lorentz-type conditions for antisymmetric fields. "We will impose a Donder-Lorentz-like gauge"
- Dilaton: A scalar field in string theory that controls the string coupling strength. "where is the vev of the dilaton"
- Einstein frame: A field redefinition in which the gravitational action takes the canonical Einstein-Hilbert form. "If we go to the Einstein frame"
- Effective field theory: A low-energy description retaining only light modes, with corrections encoded by loops and higher-dimension operators. "one can consider the one loop correction to the potential in the effective field theory"
- Flux integers: Quantized numbers specifying the amount of field-strength flux through compact cycles. "finding a family of vacua parameterized by a pair of flux integers"
- Fundamental domain: The canonical region of the moduli space (e.g., for the torus modulus) used to avoid overcounting in integrals. "over the fundamental domain of the genus one moduli space"
- Genus-one partition function: The one-loop string partition function computed on the torus world-sheet. "integrating the genus one partition function of the heterotic string compactified on "
- H3 flux: The NS-NS three-form field strength threading spacetime cycles. "The magnetic flux is the flux wrapping the "
- H7 flux: The seven-form flux Poincaré dual to the H3 flux, relevant for quantization conditions. "The correct Poincar e dual in this case is "
- Heterotic string: A string theory combining left-moving bosonic and right-moving supersymmetric sectors; here in a non-supersymmetric version. "closed string heterotic string theory"
- Intrinsically quantum vacua: Vacua that exist only due to loop corrections and not at tree level. "we have intrinsically quantum vacua for different values of "
- Knife edge solutions: Marginal critical points in moduli space that can have flat or unstable directions, sensitive to small perturbations. "so-called {\it{knife edge} solutions"
- Lattice sum: A sum over momentum and winding modes on the compactification lattice used in one-loop computations. "we present some lattice sum calculations"
- Narain moduli: The scalar parameters of the Narain lattice, including metric, B-field, and Wilson lines for toroidal compactifications. "the eighty scalars coming from the Narain moduli of the signature lattice"
- Orbifold: A quotient construction by a discrete symmetry that alters the spectrum and can break supersymmetry. "breaking supersymmetry with some orbifold/orientifold"
- Orientifold: A construction involving world-sheet parity reversal that introduces orientifold planes and can yield non-supersymmetric models. "two orientifold models i.e.~the Sugimoto model"
- Poincaré dual: The relation between a p-form and its dual (D−p)-form under Hodge duality, used to express flux quantization. "The correct Poincar e dual in this case is "
- Ricci scalar: The scalar curvature R appearing in the gravitational action, derived from the Ricci tensor. "the Ricci scalar term in \eqref{heterotic theory action}"
- S3: The three-sphere, a compact manifold with constant positive curvature. " with radius (and volume )"
- Self-dual radius: The torus radius at which momentum and winding modes are symmetric and the theory is invariant under T-duality. "a square torus at the self-dual radius"
- Spherical harmonics: Eigenfunctions on the sphere used to expand fields and analyze spectra. "expand each of these fields in spherical harmonics on "
- Sugimoto model: A non-supersymmetric orientifold model with gauge group . "the Sugimoto model"
- Tachyon: A state with negative mass-squared indicating instability in the spectrum. "it is hard to get rid of tachyons in non-supersymmetric models"
- T4: The four-torus used for compactification in string theory. ""
- Torus moduli: The parameters (metric, B-field periods, Wilson lines) characterizing the geometry and gauge background of . "The moduli coming from the torus compactification will also be above the bound"
- Uplift to de Sitter: Raising a negative-curvature (AdS) vacuum to a positive cosmological constant (dS) vacuum. "neither the uplift to deSitter nor a violation of the BF bound take place"
- Vacuum expectation value (VEV): The average value of a field in a vacuum state. "the vev of the dilaton"
- Wilson line moduli: Scalar parameters from gauge-field holonomies around torus cycles. "and Wilson line moduli"
- World-sheet supersymmetry: Supersymmetry on the two-dimensional string world-sheet, distinct from spacetime supersymmetry. "we will maintain supersymmetry on the world-sheet"
Collections
Sign up for free to add this paper to one or more collections.