KL-Regularized Reinforcement Learning is Designed to Mode Collapse (2510.20817v1)
Abstract: It is commonly believed that optimizing the reverse KL divergence results in "mode seeking", while optimizing forward KL results in "mass covering", with the latter being preferred if the goal is to sample from multiple diverse modes. We show -- mathematically and empirically -- that this intuition does not necessarily transfer well to doing reinforcement learning with reverse/forward KL regularization (e.g. as commonly used with LLMs). Instead, the choice of reverse/forward KL determines the family of optimal target distributions, parameterized by the regularization coefficient. Mode coverage depends primarily on other factors, such as regularization strength, and relative scales between rewards and reference probabilities. Further, we show commonly used settings such as low regularization strength and equal verifiable rewards tend to specify unimodal target distributions, meaning the optimization objective is, by construction, non-diverse. We leverage these insights to construct a simple, scalable, and theoretically justified algorithm. It makes minimal changes to reward magnitudes, yet optimizes for a target distribution which puts high probability over all high-quality sampling modes. In experiments, this simple modification works to post-train both LLMs and Chemical LLMs to have higher solution quality and diversity, without any external signals of diversity, and works with both forward and reverse KL when using either naively fails.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
Overview
This paper looks at how we train big AI models (like LLMs) using a method called reinforcement learning (RL) while keeping them close to how they originally behaved. A common problem is “mode collapse,” which means the model stops giving different good answers and instead repeats just one type of answer. The paper explains why this happens and offers a simple fix that makes the model give many different high-quality answers.
What is the paper trying to find out?
The authors ask:
- Do the usual RL training objectives actually lead to a diverse set of good answers?
- Does choosing “reverse KL” or “forward KL” (two ways to measure closeness between distributions) make the model more or less diverse?
- Can we change the training objective so the best possible solution is naturally diverse?
In plain terms: they want to know if the way we train models is set up to be diverse, or if it is secretly designed to collapse to one answer—and if there’s a simple way to fix it.
How did they paper it?
The paper combines math and experiments:
- Math analysis: They paper the “optimal” (best possible) distribution that RL with KL regularization would produce, assuming perfect training. Think of this as asking, “If the training succeeded perfectly, what would the model’s final behavior be?”
- Key tools:
- “Reverse KL” vs “Forward KL” are two ways to measure how close the trained model is to its original version (the “reference policy”). You can think of KL like a “closeness score.”
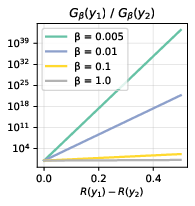
- The regularization strength (called β, “beta”) is a dial that says how strongly we force the model to stay close to its old habits.
- Rewards are points the model gets for good answers; the “reference policy” is how the model used to answer before RL.
- Simple simulations (“toy” experiments) show how different settings shape the final distribution of answers.
- Real experiments on LLMs (including creative writing and a simple math-like task) and chemical LLMs for drug discovery test their method in practice.
Analogy: Imagine you’re teaching a student to answer questions better (the reward), but you also want them to keep their writing style similar to before (the reference). The “KL” term is a rule that says “don’t change too much.” The question is: does this teaching method end up encouraging only one type of good answer, or many?
What did they find?
Here are the main findings explained simply:
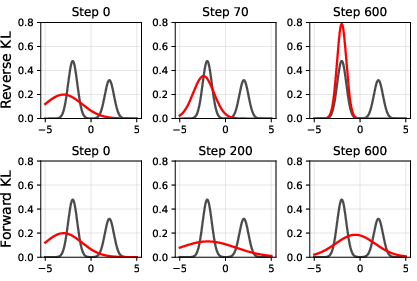
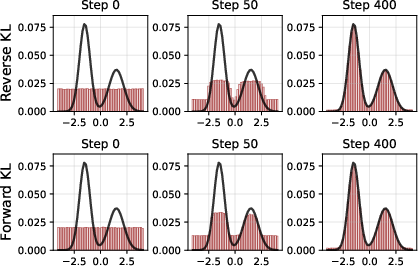
- Reverse KL vs Forward KL does not automatically decide diversity. The popular idea that “reverse KL is mode-seeking (prefers one answer) and forward KL is mass-covering (spreads across answers)” doesn’t cleanly apply in RL training of modern models. Both can produce diverse or non-diverse solutions—it depends on other factors.
- The final best distribution depends mostly on:
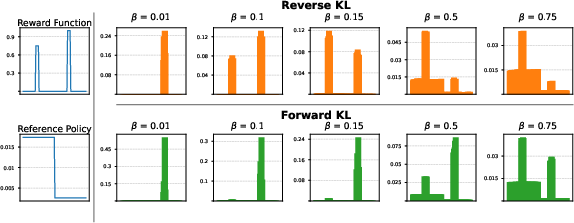
- The regularization strength (β): a dial that decides how much rewards can overpower the old habits. Small β makes the model latch onto tiny reward differences and dramatically prefer one answer.
- The size of rewards compared to the model’s old probabilities (reference policy): if two answers are equally rewarded, the model will still prefer the one it used to like more.
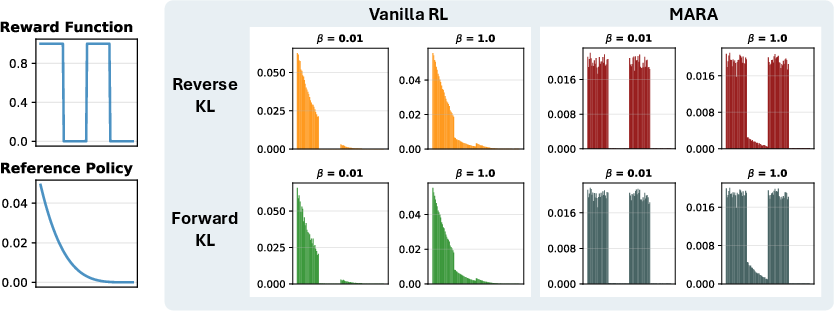
- With common RL settings, the optimal solution is often unimodal (one main answer). That means “mode collapse” is not just a training hiccup—it’s baked into the objective as currently used.
- Important detail: when multiple answers have the same reward (like “any correct answer gets 1 point”), the RL objective never boosts the rare correct answers over the common correct answers. In other words, if the model’s old habits liked answer A much more than answer B, and both are correct, standard RL won’t help B catch up.
- Both reverse and forward KL can produce multimodal distributions (many good answers), but only when β and the reward/reference balance line up just right. Small changes in β or reward scaling can flip which mode is favored.
- Forward KL regularization (as used in some recent methods) doesn’t behave like a simple “forward KL gradient” to a fixed target distribution. So you can’t rely on “mass covering” intuition alone.
A simple fix: MARA (Mode Anchored Reward Augmentation)
The authors propose MARA, a tiny change to training:
- Pick one “anchor” good answer (one the base model likes among the high-reward answers).
- Give every high-reward answer a small bonus that depends on how rare it is under the base model’s old habits.
- This makes all good answers end up with similar final probabilities, encouraging diversity without needing an external “diversity score.”
Think of MARA as: “reward all correct answers equally, and add a small extra reward to the rare ones so they can catch up.”
Why is this important?
- It explains why mode collapse happens even when training seems to go well: the objective itself often prefers one answer by design.
- It shows that simply switching KL type isn’t a sure fix; you need to shape the target distribution.
- It offers a very simple, scalable method (MARA) that improves both quality and diversity in practice.
What happened in the experiments?
They tested MARA on three kinds of tasks:
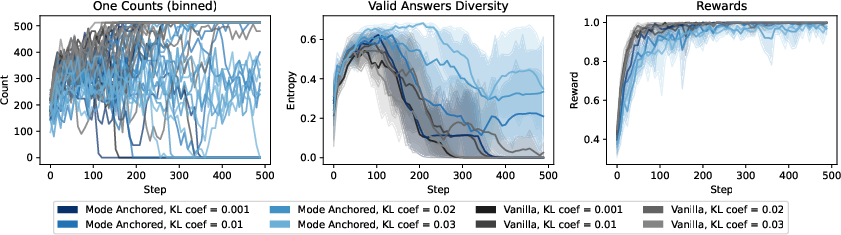
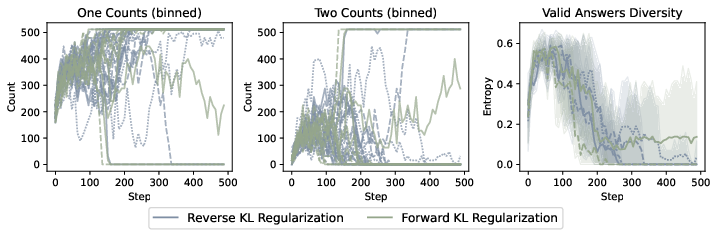
- Verifiable task (LLM that should output “1 or 2” randomly): ordinary RL collapses to always output “1” (the model’s prior favorite). MARA learns to output “1” and “2” with near-uniform probability while still formatting correctly.
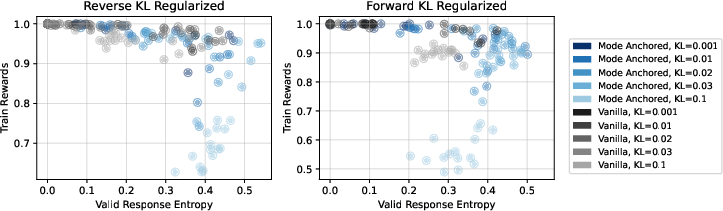
- Creative question answering (non-verifiable, uses a reward model): MARA achieved higher test-time (out-of-distribution) rewards than baselines and improved most diversity metrics.
- Drug discovery with chemical LLMs: MARA found more unique high-quality molecules faster (better yield and efficiency) while keeping similar overall diversity of chemical structures.
Bottom line and impact
- KL-regularized RL should be viewed as “distribution matching” to a target distribution created by rewards, the model’s old habits, and β. If that target distribution is unimodal, training will collapse—even if optimization is perfect.
- To get diversity, don’t just hope it happens—build it into the target distribution. MARA is a simple way to do that: it equalizes good answers by slightly boosting the rarer ones.
- This approach helps LLMs be more creative and chemical models find more varied, useful molecules, all without needing special diversity signals from outside.
In short: the paper shows why common RL post-training setups often collapse to one answer, and provides a small, principled tweak (MARA) that restores diversity while keeping quality high.
Knowledge Gaps
Below is a concise list of the paper’s unresolved knowledge gaps, limitations, and open questions that can guide future work:
- Formalize multimodality: provide a rigorous definition and measurable criteria (beyond the informal “all high-reward samples have high probability”) and connect them to provable guarantees on mode coverage in both discrete and continuous spaces.
- Forward-KL gradient characterization: fully characterize the gradient of the forward-KL–regularized reward objective, derive tractable surrogate gradients or estimators, and establish conditions under which optimization converges to the target family described by .
- Computing the forward-KL target: develop algorithms to solve for the normalization parameter in , quantify existence/uniqueness across realistic reward landscapes, and handle cases with outside the reference support.
- Token-level/step-wise extensions: extend the analysis and MARA to token-level KL penalties used in practice (e.g., PPO-style per-step KL), and clarify how per-token shaping impacts sequence-level target distributions and multimodality.
- Conditional generation: move beyond unconditional distributions and provide formal results for conditional generation , including how context-dependent and reward affect target shapes and diversity.
- Function-approximation and optimization dynamics: paper how imperfect function approximation, optimizer choice, batch noise, and early stopping affect convergence toward the intended multimodal target (for both vanilla KL-RL and MARA).
- Entropy-only regularization: provide a parallel, formal analysis for entropy-only regularization (and mixed KL+entropy), detailing probability ratios and mode coverage, and compare against KL-regularized behavior.
- Automatic scaling and tuning: develop principled methods to adapt online (or per-context) based on reward magnitude and reference probabilities to achieve desired mode coverage, rather than fixed hyperparameters.
- Robustness to reward errors: analyze sensitivity of both vanilla KL-RL and MARA to noisy, biased, or misspecified reward models; propose robust variants (e.g., confidence-weighted or distributionally robust MARA).
- Anchor selection in MARA: evaluate the sensitivity of MARA to anchor choice (e.g., among high-reward samples), paper anchoring bias, and design alternative anchoring strategies (multi-anchor sets, stochastic anchors, or anchors chosen by diversity heuristics).
- Thresholding strategy: formalize the choice of (fixed, adaptive, percentile-based) and its impact on coverage, stability, and quality; provide guidance for tasks with unknown reward ranges or evolving reward distributions.
- Stationarity and batch effects: analyze the non-stationarity introduced by batch-wise anchors and thresholds in MARA, and propose memory-based or global set maintenance to stabilize the target distribution over training.
- Safety and undesired modes: investigate failure modes where “high reward” includes unsafe or undesirable outputs due to reward misspecification, and incorporate safety constraints or veto mechanisms compatible with MARA’s diversity objectives.
- Theoretical guarantees for MARA: prove conditions under which MARA yields uniform (or controlled) probability across high-reward sets, quantify trade-offs with proximity to , and characterize coverage in continuous/high-dimensional spaces.
- Generalization beyond KL: explore designing target families using other -divergences, integral probability metrics, or optimal transport to achieve specific diversity profiles, and compare their optimization properties to KL-based targets.
- Calibration and coherence: measure how diversity-targeting (MARA or others) affects calibration, perplexity, and coherence, and develop methods to preserve these properties while expanding mode coverage.
- Exploration impacts: analyze whether MARA improves exploration in long-horizon tasks and credit assignment, and quantify sample-efficiency benefits relative to count-based or entropy bonuses.
- Practical RLHF integration: demonstrate MARA within large-scale RLHF pipelines (on-policy/off-policy), with real human preference data, and report compute, stability, and throughput costs relative to standard baselines.
- Human evaluation of diversity: complement automatic metrics (n-grams, embeddings, distinct classes) with rigorous human evaluations of perceived diversity, novelty, and utility, and correlate these with reward improvements.
- Larger-scale and broader benchmarks: test across more models (larger LLMs), domains, and tasks (reasoning, coding, safety-critical), and compare MARA to other diversity-oriented baselines (e.g., GFlowNets, diverse DPO variants, unlikelihood training).
- Pass@k and coverage metrics: report pass@k, coverage of distinct solution families, and mode balance (e.g., per-mode entropy/frequency) to validate that increased diversity translates into practical multi-solution performance.
- Reference model estimation issues: paper how inaccuracies or calibration errors in (e.g., token-level vs trajectory-level estimators) affect the target distribution and MARA’s reward augmentation.
- Off-support behavior under forward KL: translate the theoretical allowance for nonzero mass outside into practical algorithms that avoid conflicts with token-level KL penalties commonly used in training.
- Chemical LM validation: expand CLM experiments to more objectives and datasets, evaluate synthesis-route realism, scaffold/functional-group coverage, and—where possible—empirical validation (wet-lab or trusted simulators) of discovered molecules.
- Computational overhead and stability: quantify MARA’s additional computation (anchor selection, per-sample augmentation), its impact on training stability, and whether any efficiency gains (e.g., in CLMs) generalize across domains.
- Adaptive target design: investigate dynamic target shaping that interpolates between “uniform over high-reward modes” and “reward-proportional mass,” enabling control over diversity-quality trade-offs during training or deployment.
Practical Applications
Immediate Applications
The paper’s findings and the MARA algorithm enable several practical changes that can be deployed now across RLHF pipelines, model post-training, and domain-specific generative systems.
- Diverse RLHF post-training for LLMs (software, media, education)
- Action: Integrate Mode Anchored Reward Augmentation (MARA) into existing reverse-KL or GRPO/RLOO-style pipelines to preserve diversity without sacrificing reward. Use a per-batch “anchor” (highest reference log-prob among high-reward samples) and augment rewards for all samples above a threshold τ.
- Tools/Workflows: Modify reward computation in RLHF loops (two-line change), add τ selection (static for verifiable tasks; percentile-based for non-verifiable tasks), and log-prob access from the base/reference model.
- Assumptions/Dependencies: Requires reliable reward signals, access to reference policy log-probs, and appropriate τ selection; assumes existence of multiple high-reward modes.
- Auditing and correcting KL regularization practices (software, academia, MLOps)
- Action: Audit pipelines that assume “forward KL = mass covering” (e.g., GRPO defaults) and align practice with theory (the forward-KL-regularized reward objective is not a forward-KL gradient). Where diversity is collapsing, switch to MARA or adjust β relative to reward/reference magnitudes.
- Tools/Workflows: Training governance checklist; unit tests verifying target distribution properties under current β; developer docs clarifying gradient interpretations.
- Assumptions/Dependencies: Access to training objectives and gradients; willingness to adjust hyperparameters and reward shaping.
- Hyperparameter calibration using β–reward–reference relationships (software)
- Action: Use the log-prob ratio identity to set β that balances high-reward/low-support vs. lower-reward/high-support modes (solve R(y2)−R(y1)=β[log πref(y1)−log πref(y2)] to equalize target probabilities).
- Tools/Workflows: “β calculator” utility; training dashboards displaying per-batch reward and reference log-prob differentials; early stopping based on diversity/quality Pareto fronts.
- Assumptions/Dependencies: Accurate reward magnitudes; stable reference probabilities over training; representative batches.
- Verifiable reasoning tasks with multiple correct answers (education, software)
- Action: For tasks with equal rewards among correct answers (e.g., math solvers), use MARA to avoid implicit preference for high-support modes and improve pass@k and multi-solution coverage.
- Tools/Workflows: Set τ to the known correctness reward; anchor to the highest-support correct solution; report valid-answer entropy alongside reward.
- Assumptions/Dependencies: Binary/verifiable reward available; base model has non-zero support over multiple correct solutions.
- Creative content generation with diversity guarantees (media, consumer apps)
- Action: Deploy “Diverse RL Post-Training” for chat and writing assistants to increase n-gram and semantic diversity while improving out-of-distribution reward (quality) scores.
- Tools/Workflows: MARA in reward-model-based training; “Diverse Drafts” feature exposing multiple high-quality modes; diversity metrics in product analytics.
- Assumptions/Dependencies: Reward model fidelity; careful τ selection (upper percentile of rewards) to avoid gaming; monitor for safety filters and moderation constraints.
- Drug discovery with CLMs (healthcare/pharma)
- Action: Integrate MARA into REINVENT-like pipelines to increase yield of unique high-reward molecules and improve optimization efficiency (lower OB100), while maintaining global diversity.
- Tools/Workflows: Reward augmentation with synthesizability/potency signals; diversity monitoring via IntDiv and substructure metrics; batch-wise anchors among high-reward candidates.
- Assumptions/Dependencies: Access to reliable simulation-based reward functions; budget for expensive evaluations; chemical validity constraints via the prior.
- Training monitoring and diversity dashboards (software, MLOps)
- Action: Add diversity metrics (valid-answer entropy, n-gram diversity, embedding diversity) alongside reward during RLHF and CLM training to detect and remediate mode collapse early.
- Tools/Workflows: Pareto front tracking (quality vs. diversity); alerting when entropy falls below threshold; automatic switch to MARA or β re-tuning.
- Assumptions/Dependencies: Robust metric implementations; computational budget for evaluation; defined diversity thresholds per task.
- Batch-level data filtering interpreted as target-distribution matching (academia, software)
- Action: Reframe STaR/RAFT-style filtering as approximating a target distribution that prioritizes high-reward regions; use MARA to make the implicit target explicitly multimodal.
- Tools/Workflows: Combine high-reward filtering with reward augmentation; maximum-likelihood fine-tuning toward a diverse target when feasible.
- Assumptions/Dependencies: Sufficient high-reward samples; tractable sampling and optimization; consistency between filtering and augmented reward design.
Long-Term Applications
Beyond immediate integration, the paper suggests broader shifts toward explicit target distribution design, diversity-aware alignment, and cross-domain multi-solution planning.
- Target distribution design frameworks (software, research tooling)
- Vision: Build libraries that let practitioners specify desired properties (e.g., uniform mass over high-reward modes) and auto-derive reward augmentations or regularizer schedules.
- Tools/Products: “Target Distribution Studio” with MARA-like templates, dynamic τ, anchor ensembles, and visualization; integration with popular RLHF frameworks.
- Assumptions/Dependencies: Standardized interfaces for reward models and reference policies; best practices for stability and convergence.
- Diversity-aware AI alignment guidelines (policy, governance)
- Vision: Incorporate diversity preservation into standards for RLHF and generative AI procurement (avoid homogenization, encourage multi-hypothesis outputs in sensitive domains).
- Tools/Products: Auditing protocols requiring quality-diversity reporting; minimum entropy thresholds; documented β calibration and reward augmentation strategies.
- Assumptions/Dependencies: Sector-specific safety requirements; measurable diversity utility; regulatory adoption.
- Multi-hypothesis clinical decision support (healthcare)
- Vision: Clinical AI systems that present multiple high-quality treatment pathways rather than a single recommendation, aligning with human oversight and uncertainty representation.
- Tools/Products: MARA-augmented decision engines paired with verifiable outcomes and confidence calibration; workflows for shared decision-making.
- Assumptions/Dependencies: Validated reward models capturing patient outcomes; regulatory and ethical approval; strong human-in-the-loop safeguards.
- Diverse planning in robotics (robotics)
- Vision: Maintain multiple feasible plans for navigation/manipulation under uncertain constraints via anchored reward augmentation to avoid collapsing to a single plan.
- Tools/Products: Planning stacks that expose diverse high-reward trajectories; scenario-based evaluation for robustness.
- Assumptions/Dependencies: Task formulations with verifiable multi-solution outcomes; reliable priors over action spaces; safety constraints monitored.
- Scenario generation in energy and climate modeling (energy, public sector)
- Vision: Generate diverse, high-quality scenarios for grid operations or policy stress testing, avoiding over-commitment to single-mode strategies.
- Tools/Products: MARA-enabled scenario generators tied to simulation rewards; dashboards for comparing outcomes across modes.
- Assumptions/Dependencies: Accurate simulation-based reward models; domain-expert validation; compliance with reliability standards.
- Multi-strategy synthesis in finance (finance)
- Vision: Produce diverse strategies that balance risk-adjusted return while avoiding overfitting a single historical mode; use anchors to stabilize against low-support over-exploration.
- Tools/Products: Strategy generators with MARA; portfolio construction tools that sample across modes; stress testing across regimes.
- Assumptions/Dependencies: High-quality reward models (Sharpe/Sortino, drawdown penalties); strict risk controls and compliance; robust backtesting.
- Advanced forward-KL optimization methods (academia, software)
- Vision: Develop tractable approximations to forward-KL gradients toward multimodal targets (e.g., sampling from Gfwd), enabling principled mass-covering behavior at scale.
- Tools/Products: New estimators and training objectives; hybrid KL methods; improved theoretical guarantees.
- Assumptions/Dependencies: Efficient sampling from complex targets; variance reduction techniques; convergence analyses.
- Education: multi-solution tutoring systems (education)
- Vision: Tutoring LLMs that consistently present several correct solution paths and styles (analytic, visual, heuristic), improving learning outcomes and critical thinking.
- Tools/Products: MARA-based reward shaping for correctness and explanation quality; classroom analytics of diversity.
- Assumptions/Dependencies: Reliable correctness checking; classroom safety policies; equitable access to diverse solutions.
- Benchmarking and metrics standardization for diversity (academia, industry consortia)
- Vision: Establish diversity benchmarks and reporting standards (e.g., NoveltyBench-like suites) alongside quality metrics across tasks and sectors.
- Tools/Products: Open benchmarks, leaderboards tracking quality-diversity Pareto fronts; shared best practices for τ and anchor selection.
- Assumptions/Dependencies: Community adoption; cross-dataset comparability; careful metric design to avoid gaming.
Cross-cutting assumptions and dependencies
- Access to a reference policy and its log-probabilities for trajectories (a standard requirement in KL-regularized RLHF).
- Reliable reward functions or reward models; τ selection that correctly identifies “high-quality” regions without introducing reward hacking.
- Existence of multiple high-reward modes; if high-reward regions lie entirely outside the reference support, forward-KL behavior differs and may need specialized handling.
- Training stability and governance: monitoring for safety, fairness, and mode collapse; clear documentation of β calibration and reward augmentation logic.
Glossary
- Count-based exploration bonus: An exploration strategy that adds reward bonuses to rarely seen outcomes or states to encourage coverage of the space. "count-based exploration bonuses"
- Entropy-only regularization: A regularization term that encourages higher-entropy (more spread-out) policies without explicitly matching a reference distribution. "Note this issue is identically present for entropy-only regularization"
- f-divergence: A broad class of divergence measures (including KL) defined via a convex function, used to regularize or compare distributions. "a more general class of -divergence regularizers"
- Forward KL divergence: The KL divergence , often associated with “mass covering” behaviour when approximating a target distribution. "we refer to as the forward KL divergence"
- GFlowNets: Generative Flow Networks that learn to sample objects proportionally to reward by enforcing flow consistency, often used for diverse discovery. "GFlowNets also provide diversity-seeking policies that are specifically designed to sample proportionally to reward"
- GRPO: A policy optimization method used in LLM post-training that can effectively estimate a forward-KL-style objective. "such as GRPO \citep{shao2024deepseekmath,guo2025deepseek}—may have incidentally estimated the forward KL"
- KL-regularized RL: Reinforcement learning objectives augmented with a KL penalty to keep the learned policy close to a reference distribution. "KL-regularized RL is inherently a distribution matching problem and should be viewed as such"
- Kullback–Leibler (KL) divergence: A measure of discrepancy between probability distributions used widely in inference and learning. "The Kullback–Leibler (KL) divergence \citep{kullback1951information} measures the discrepancy between two probability distributions"
- MARA (Mode Anchored Reward Augmentation): A reward-modification technique that equalizes high-reward modes by anchoring to a high-support sample, promoting multimodality. "Mode Anchored Reward Augmentation (MARA)"
- Mass covering: The intuition that forward KL spreads probability across all regions where the target has mass. "forward KL is often described as “mass covering”"
- Maximum likelihood: A training approach that maximizes the likelihood of observed (or selected) trajectories, equivalent to supervised fine-tuning in LMs. "It in fact reduces to doing maximum likelihood (supervised fine-tuning) on trajectories sampled from the target "
- Mode anchoring: Selecting a representative high-reward, high-support sample as an anchor to adjust rewards and balance probabilities across good modes. "we colloquially refer to this as “mode anchoring”"
- Mode collapse: The phenomenon where a model’s output distribution concentrates on few modes, reducing diversity. "KL-Regularized Reinforcement Learning is Designed to Mode Collapse"
- Mode seeking: The intuition that reverse KL concentrates probability on high-density regions of the target, potentially preferring a single mode. "Reverse KL is often described as “mode seeking”"
- Normalizing constant: The partition function that ensures a distribution integrates/sums to one. "where $= \int (y) \exp (\nicefrac{R(y)}{\beta} ) \, d y$ is the normalizing constant"
- Pareto front: The set of models that optimally trade off multiple objectives (e.g., quality and diversity) without being dominated on all axes. "the Pareto front of model checkpoints at different points in training shows"
- RAFT: A trajectory-filtering and distillation method that trains via maximum likelihood on selected high-reward samples. "STaR \citep{zelikman2022star} and RAFT \citep{dong2023raft,xiong2024raftplus}"
- Reward model: A learned scorer that provides scalar feedback on outputs for alignment or quality optimization. "using a parametric reward model (Skywork-Reward-V2-Qwen3-4B)"
- Reverse KL divergence: The KL divergence , often associated with “mode seeking” behaviour when approximating a target distribution. "we refer to as the reverse KL divergence"
- RLOO: A policy gradient estimator that uses a leave-one-out baseline to reduce variance in reinforcement learning updates. "MARA is used as a drop-in replacement in an RLOO style algorithm"
- STaR: Self-Taught Reasoner; a method that filters high-reward trajectories and trains via supervised learning to improve reasoning. "STaR \citep{zelikman2022star} and RAFT \citep{dong2023raft,xiong2024raftplus}"
- Support (of a distribution): The set of outcomes with nonzero probability under a distribution. "outside of $$'s support"</li> <li><strong>Target distribution</strong>: The distribution implicitly defined by rewards, regularization, and a reference policy that the RL objective pushes the policy to match. "minimizing a reverse KL toward the target distribution $G_\beta$"
- Variational inference (VI): An optimization framework that approximates complex posteriors with tractable distributions by minimizing a divergence. "tools from variational inference (VI)"
- Verifiable reward: A ground-truth reward computed by deterministic checks (e.g., correctness), without a learned model. "a standard set-up for RL with verifiable reward (e.g. math)"
Collections
Sign up for free to add this paper to one or more collections.