Papers
Topics
Authors
Recent
Assistant
AI Research Assistant
Well-researched responses based on relevant abstracts and paper content.
Custom Instructions Pro
Preferences or requirements that you'd like Emergent Mind to consider when generating responses.
Gemini 2.5 Flash
Gemini 2.5 Flash 134 tok/s
Gemini 2.5 Pro 41 tok/s Pro
GPT-5 Medium 21 tok/s Pro
GPT-5 High 25 tok/s Pro
GPT-4o 92 tok/s Pro
Kimi K2 196 tok/s Pro
GPT OSS 120B 431 tok/s Pro
Claude Sonnet 4.5 37 tok/s Pro
2000 character limit reached

Why DPO is a Misspecified Estimator and How to Fix It (2510.20413v1)

Published 23 Oct 2025 in cs.LG

Abstract: Direct alignment algorithms such as Direct Preference Optimization (DPO) fine-tune models based on preference data, using only supervised learning instead of two-stage reinforcement learning with human feedback (RLHF). We show that DPO encodes a statistical estimation problem over reward functions induced by a parametric policy class. When the true reward function that generates preferences cannot be realized via the policy class, DPO becomes misspecified, resulting in failure modes such as preference order reversal, worsening of policy reward, and high sensitivity to the input preference data distribution. On the other hand, we study the local behavior of two-stage RLHF for a parametric class and relate it to a natural gradient step in policy space. Our fine-grained geometric characterization allows us to propose AuxDPO, which introduces additional auxiliary variables in the DPO loss function to help move towards the RLHF solution in a principled manner and mitigate the misspecification in DPO. We empirically demonstrate the superior performance of AuxDPO on didactic bandit settings as well as LLM alignment tasks.

Summary

  • The paper demonstrates that DPO is a misspecified estimator for parametric policy classes, leading to issues like preference reversal and reward degradation.
  • It introduces AuxDPO, using auxiliary variables to explore the full reward equivalence class, thereby restoring optimal RLHF alignment.
  • Empirical results on synthetic and LLM alignment tasks confirm AuxDPO’s superiority, robustness to model capacity, and consistent performance.

Why DPO is a Misspecified Estimator and How to Fix It

Introduction and Motivation

Direct Preference Optimization (DPO) has become a widely adopted method for aligning LLMs with human preferences, offering a computationally efficient alternative to two-stage RLHF (Reinforcement Learning from Human Feedback). DPO circumvents the need for explicit reward model training and on-policy rollouts by reparameterizing the RLHF objective into a single supervised learning phase. However, this paper rigorously demonstrates that DPO is fundamentally a misspecified estimator when applied to parametric policy classes, such as neural networks, rather than the idealized tabular setting. The misspecification leads to several critical failure modes, including preference order reversal, reward degradation, and high sensitivity to the distribution of preference data. The authors propose AuxDPO, a principled extension of DPO that introduces auxiliary variables to mitigate these issues and empirically validate its superiority across synthetic and real-world LLM alignment tasks.

Theoretical Analysis: Misspecification in DPO

The core insight is that DPO, when applied to parametric policy classes, solves a weighted reverse-KL projection of the true reward function r∗r^* onto the lower-dimensional manifold of reward functions expressible by the policy class. In the tabular case, this projection is exact, and DPO recovers the RLHF-optimal policy. However, for neural policies, r∗r^* is almost always outside the expressible manifold, resulting in a misspecified estimation problem. The projection is governed by the empirical frequencies of preference data, making the learned policy highly sensitive to data distribution.

This geometric perspective is illustrated in the following figure: Figure 1

Figure 1: DPO projects the true reward function r∗r^* onto the implicit reward manifold of the policy class; misspecification leads to unreliable solutions, while AuxDPO introduces degrees of freedom to approach the RLHF solution.

The authors formalize this with a local linearization of the reward manifold and show that, in the large-β\beta regime (strong KL regularization), the implicit reward functions are well-approximated by the column space of the policy gradient matrix. This enables a precise characterization of the error induced by misspecification and its dependence on the preference data distribution.

Empirical Failure Modes of DPO

Through a synthetic example with three actions and a one-dimensional policy parameter, the paper demonstrates several pathologies:

  • Preference Reversal: DPO can learn a policy that prefers a suboptimal action over the optimal one, depending on the imbalance in pairwise preference counts.
  • Reward Reduction: The expected reward of the learned policy can be strictly lower than that of the base policy, contradicting the monotonic improvement guarantee of RLHF.
  • Sensitivity to Data Distribution: The learned policy is highly sensitive to the empirical distribution of preference pairs, leading to inconsistent outcomes.

These phenomena persist even in the data-rich regime with infinite clean preference data, highlighting that the issue is intrinsic to the geometry of the parametric policy class rather than sample scarcity.

Geometric Characterization of RLHF and the AuxDPO Solution

The authors analyze the local geometry of RLHF optimization and show that, for parametric policies, the set of reward functions yielding the same optimal policy forms an equivalence class differing by elements in the null space of the scaled policy gradient matrix. DPO, by contrast, only searches over the minimum-norm representative of this class, which is insufficient to recover the RLHF solution under misspecification.

AuxDPO addresses this by augmenting the DPO loss with auxiliary variables δ\delta constrained to the null space, allowing the optimization to explore the full equivalence class and reliably recover the RLHF-optimal policy. The optimization is formulated as a constrained minimization of the DPO loss over both policy parameters and auxiliary variables, with practical implementations using either exact null-space parameterization (for small models) or batchwise soft penalties (for large models).

This mechanism is depicted in the following figure: Figure 2

Figure 2: AuxDPO augments the search space with null-space degrees of freedom, enabling projection onto the RLHF equivalence class and recovery of the optimal policy.

Experimental Results

The empirical evaluation spans synthetic bandit settings and large-scale LLM alignment tasks using MMLU-Pro and RewardBench v2. Key findings include:

  • Superior Alignment: AuxDPO consistently outperforms DPO, IPO, and DPOP in both in-domain (ID) and out-of-domain (OOD) settings, achieving higher accuracy on held-out human preference data.
  • Robustness to Model Capacity: AuxDPO maintains its advantage even when the number of trainable parameters is severely restricted (e.g., LoRA or last-layer tuning), demonstrating robustness to model expressibility constraints.
  • Mitigation of Failure Modes: In synthetic experiments, AuxDPO avoids preference reversal and reward degradation, reliably increasing expected reward regardless of preference data distribution.

The following figures summarize the comparative performance across models and parameter budgets: Figure 1

Figure 1: Final evaluation accuracy for Qwen-3-0.6B and Llama-2.3-1B on MMLU-Pro and RewardBench-V2, showing AuxDPO's consistent gains over DPO across trainable parameter fractions.

Figure 2

Figure 2: Llama-2.1-8B results on MMLU-Pro and RewardBench-V2, comparing DPO, AuxDPO, IPO, and DPOP; AuxDPO achieves the highest accuracy in both ID and OOD settings.

Implementation Considerations

AuxDPO is implemented as an extension of the TRL DPOTrainer, requiring only modest additional memory for auxiliary variables. For small models, the null-space constraint can be enforced exactly via SVD; for large models, a batchwise penalty suffices. The computational overhead is negligible compared to the gains in alignment performance. The method is compatible with standard optimization schedules and can be integrated into existing preference optimization pipelines with minimal changes.

Implications and Future Directions

The paper's analysis reveals that DPO's equivalence to RLHF is contingent on the tabular policy assumption, which is violated in practical neural architectures. Misspecification leads to unpredictable and sometimes detrimental outcomes, especially in low-capacity or data-imbalanced regimes. AuxDPO provides a principled fix, restoring the theoretical guarantees of RLHF in parametric settings and offering robust empirical performance.

Future research may explore:

  • Extension of AuxDPO to more general forms of preference data (e.g., KK-wise comparisons, trajectory-level feedback).
  • Integration with distributionally robust or privacy-preserving preference optimization frameworks.
  • Analysis of the interaction between auxiliary variable regularization and generalization in large-scale LLMs.
  • Application to multi-objective or pluralistic alignment scenarios.

Conclusion

This work establishes that DPO is a misspecified estimator in parametric policy classes, leading to critical failure modes in preference-based alignment. The proposed AuxDPO algorithm introduces auxiliary variables to circumvent misspecification, achieving alignment performance matching or exceeding RLHF in both theory and practice. The geometric framework and empirical results provide a foundation for principled direct alignment methods in modern LLMs and highlight the necessity of addressing model misspecification in preference optimization.

File Document Download Save Streamline Icon: https://streamlinehq.com PDF File Document Download Save Streamline Icon: https://streamlinehq.com Markdown
Ai Generate Text Spark Streamline Icon: https://streamlinehq.com

Explain it Like I'm 14

What is this paper about?

This paper studies how we teach LLMs to prefer better answers using “preference data” (pairs of a good and a bad response). It looks closely at a popular, simple training method called Direct Preference Optimization (DPO) and shows that DPO can be mathematically “misspecified” — meaning it often tries to learn the wrong thing when models have limited flexibility. The authors explain why this happens, what goes wrong, and introduce a fix called AuxDPO that makes DPO behave more like a stronger method called RLHF (Reinforcement Learning with Human Feedback), but without the heavy extra work.

What questions are the authors asking?

In simple terms, the paper asks:

  • When we use DPO to align a LLM with human preferences, does it still work well if the model can’t represent every possible behavior?
  • If it doesn’t, what kinds of failures can happen?
  • Can we change DPO in a principled way so it acts more like RLHF and avoids those failures?

How did they paper it? Key ideas and methods

To make the ideas easier to grasp, here are the main concepts with everyday analogies:

  • Preference alignment: The model sees pairs of responses for a prompt: one preferred (chosen) and one not preferred (rejected). The goal is to make the model more likely to produce the chosen kind of responses.
  • Reward function: Think of a “reward” as a score the model gives to each response. Higher scores mean better responses. Preferences come from comparing two scores: if score A > score B, we prefer A.
  • RLHF vs DPO:
    • RLHF is a two-step process: first train a reward model to score responses, then run reinforcement learning to push the model toward higher-reward answers while staying close to its original behavior.
    • DPO is a faster, one-step shortcut: it tries to directly optimize the model using the preference pairs, without training a separate reward model or doing full reinforcement learning.
  • Tabular vs parametric policies:
    • Tabular (idealized): Imagine a super-flexible spreadsheet that can store any probability for any prompt-response pair. In this ideal world, DPO’s math lines up perfectly.
    • Parametric (real LLMs): Real models have a limited number of parameters. They can’t represent every possible behavior. This limitation is where DPO’s problems begin.
  • Geometry and projection analogy:
    • Picture the “true reward function” (the perfect scoring system that generated the preferences) as a point in space.
    • DPO can only move within a lower-dimensional surface (a “manifold”) defined by what the model class can represent.
    • DPO “projects” the true reward onto this surface. If the true reward isn’t on that surface, the projection may land in the wrong place — leading to mismatches with real preferences.
  • Local linearization (zooming in):
    • The authors “zoom in” around the current model, approximating curves by straight lines (like straightening a small section of a bendy road). This makes the math clearer and shows precisely how DPO moves when the model’s flexibility is limited.
  • Equivalence classes (same policy from different rewards):
    • In RLHF, many different reward functions can lead to the same best policy change. Think of different recipes that produce the same taste — the exact recipe differs, but the end result (the policy) is the same.
    • This viewpoint lets the authors define the “right” direction to move the policy, even when the reward is misspecified.
  • AuxDPO (the fix):
    • The authors add “auxiliary variables” — extra knobs the optimizer can turn — that live in directions the base model can’t “feel” (called the null space).
    • By adding these controlled degrees of freedom, AuxDPO can steer the learned reward closer to the one RLHF would effectively use, even if the original DPO would miss it.

What did they find, and why is it important?

Here are the main findings:

  • DPO is a misspecified estimator in real models:
    • When the true reward can’t be perfectly represented by the model class, DPO ends up fitting the closest representable reward, not the true one. This “closest” depends on how often different preference pairs appear in the dataset.
    • In other words, DPO acts like a weighted projection of the true reward onto the model’s limited reward surface. The weights come from the frequencies of preference pairs.
  • Failure modes can occur even with clean, abundant data:
    • Preference order reversal: DPO can make the model increase the probability of a worse answer over a better one.
    • Reward reduction: The model’s average reward (how good its answers are) can actually go down compared to the base model, which shouldn’t happen with good alignment.
    • Sensitivity to data distribution: Small changes in how often certain pairs appear can flip outcomes, making DPO brittle.
  • RLHF’s local behavior looks like a “natural gradient” step:
    • The authors show that, near the base model, RLHF moves the policy in a specific direction that accounts for the model’s shape (like hiking with a map that shows the slope steepness). This ties RLHF to a well-understood, stable update rule.
  • AuxDPO mitigates misspecification:
    • By adding auxiliary variables constrained to the “null space” (directions that don’t alter certain model signals), AuxDPO finds reward representations that better match RLHF’s ideal behavior.
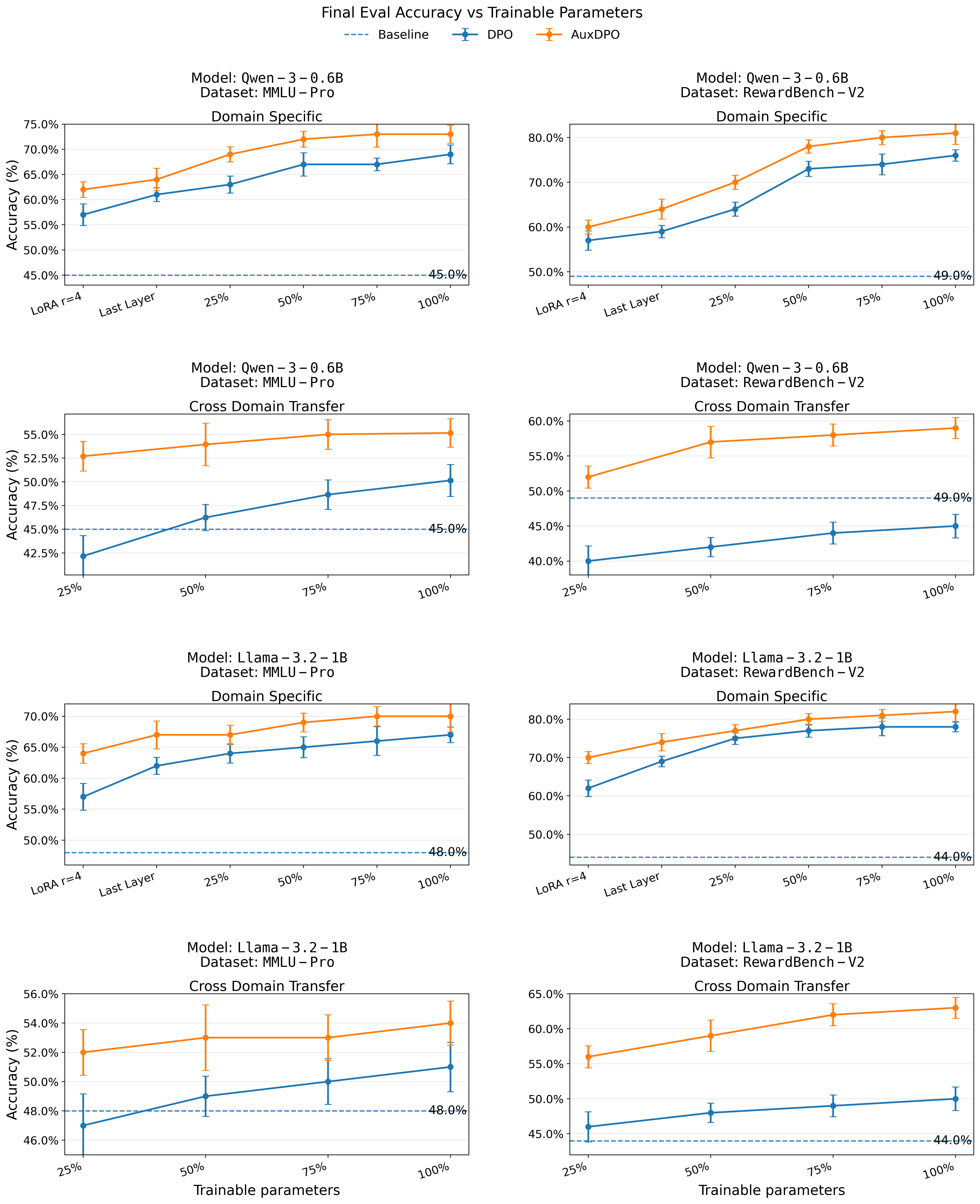
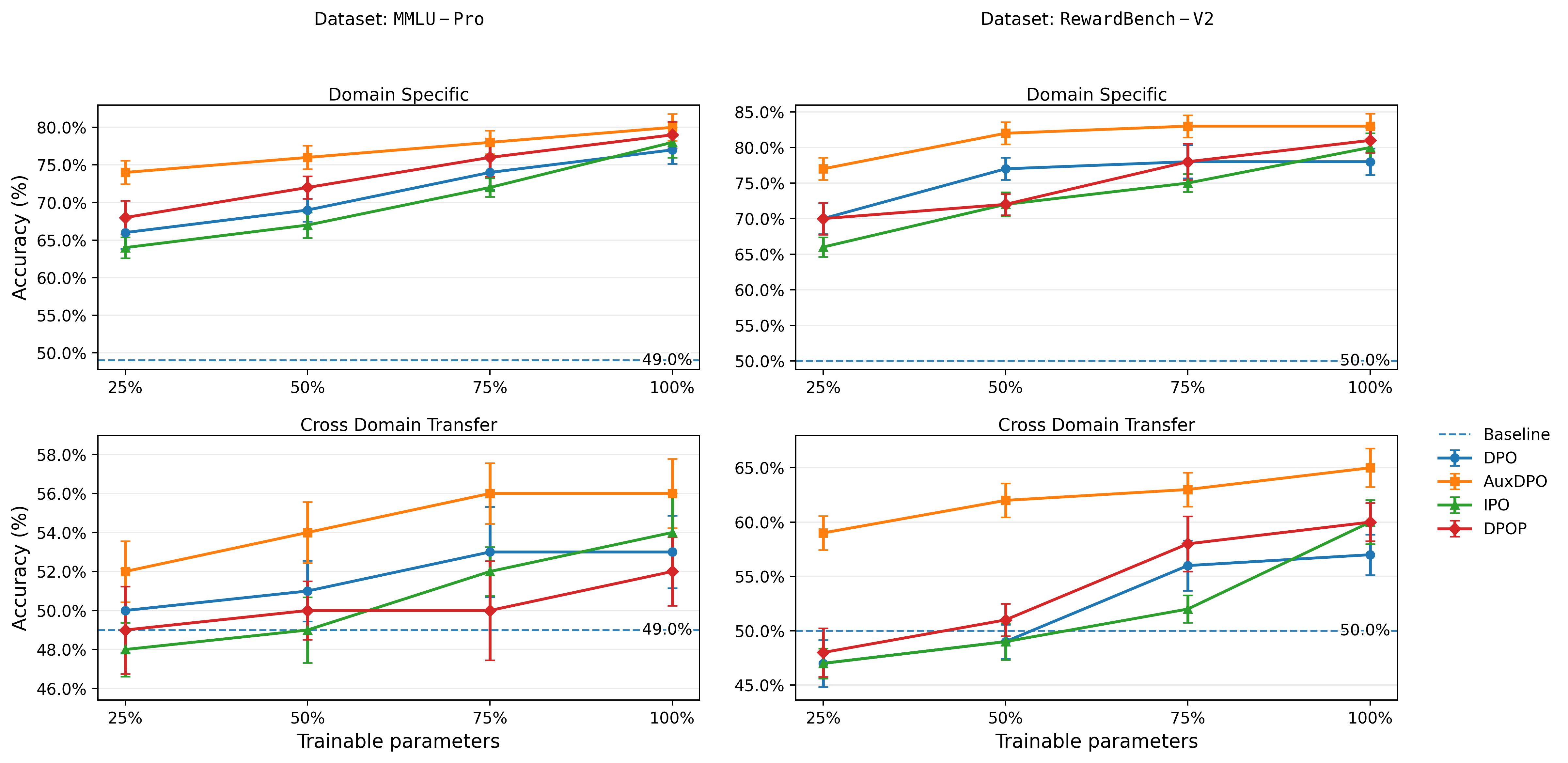
    • In experiments (simple bandit problems and LLM tasks like RewardBench v2 and MMLU-Pro), AuxDPO consistently outperforms standard DPO, aligning better with held-out human preferences.

Why this matters: Many teams use DPO because it’s simple and cheaper than full RLHF. This paper shows DPO can behave unexpectedly when models are limited — which they always are. AuxDPO offers a practical way to keep the simplicity of DPO while avoiding its worst pitfalls.

What’s the impact of this research?

  • It cautions researchers and practitioners: Don’t assume DPO is always a safe RLHF replacement. Its results can depend strongly on your preference data’s composition and the model’s capacity.
  • It provides a principled upgrade: AuxDPO keeps the lightweight feel of DPO but brings it closer to RLHF’s reliable behavior. That means better alignment with fewer resources.
  • It suggests better data practices: Because standard DPO is sensitive to which pairs you include and how often, being mindful of data collection and balance is important. AuxDPO reduces this sensitivity.
  • It advances understanding of alignment geometry: Viewing alignment through geometry and projections helps explain failures and guide fixes, giving a clearer map for future algorithm design.

Overall, the paper deepens our understanding of how simple alignment methods behave in real-world models and offers a practical improvement that can make LLMs more reliably follow human preferences.

Ai Sparkles Streamline Icon: https://streamlinehq.com View Paper Prompt List Streamline Icon: https://streamlinehq.com View All Prompts
Ai Generate Text Spark Streamline Icon: https://streamlinehq.com

Knowledge Gaps

Knowledge gaps, limitations, and open questions

Below is a single, concrete list of what remains missing, uncertain, or unexplored in the paper, organized for actionability.

Theory: assumptions and scope

  • The analysis and guarantees rely on the large-β\beta local regime; behavior and guarantees for moderate or small β\beta (nonlocal moves away from the base policy) are not characterized.
  • The equivalence and misspecification results assume a Bradley–Terry–Luce (BTL) preference model; robustness to non-BTL preferences, annotator inconsistencies, or context-dependent preferences is not analyzed.
  • The RLHF objective is assumed to have a unique minimizer; conditions for uniqueness, handling multi-modal optima, and tie-breaking are not provided.
  • The theory assumes finite state and action spaces; extending the geometric characterization and AuxDPO to sequence-level generation (token-level actions, infinite vocabularies, long-horizon dependencies) is left open.
  • The implicit reward manifold Rβ\mathcal{R}^\beta is only locally linearized; its global geometry (dimension, curvature, identifiability) for real LLM policy classes is not described or measured.
  • Reverse-KL weighting by pairwise counts is central to the DPO projection; alternative divergences (e.g., forward KL, Bregman projections) and their impact on misspecification and stability are not explored.
  • Sensitivity to the preference data distribution (counts ns,a,a′n_{s,a,a'}) is shown, but no sufficient conditions, reweighting schemes, or sampling strategies are provided to guarantee DPO success under parametric policies.

Algorithm design and practicality

  • Computing Aρ,θ0A_{\rho,\theta_0} and Fρ,θ0F_{\rho,\theta_0} for large LLMs requires gradients over the action space; there is no guidance on scalable approximation, variance control, or error bounds for these quantities.
  • The null-space constraint on auxiliary variables (δ∈N(Aρ,θ0)\delta \in \mathcal{N}(A_{\rho,\theta_0})) is enforced via a Monte Carlo penalty; consistency guarantees, bias/variance analysis, and principled tuning of the penalty coefficient λ\lambda are missing.
  • AuxDPO assumes a fixed reference policy πθ0\pi_{\theta_0}; how to update Aρ,θ0A_{\rho,\theta_0} and the null space as θ\theta changes during training (and whether to re-linearize iteratively) is not specified.
  • Auxiliary variables δ\delta are introduced per training pair; the risk of overfitting to specific pairs, memory footprint for large datasets, and strategies for parameter sharing or regularization are not analyzed.
  • It is unclear how δ\delta is used at inference time (if at all); a precise training-to-inference pathway showing that learned δ\delta leads to a stable policy update equivalent to RLHF in practice is not provided.
  • Stability under limited coverage (when πθ0(a∣s)\pi_{\theta_0}(a\mid s) is near-zero) and numerical issues with ∇log⁡πθ0\nabla\log\pi_{\theta_0} are not addressed.
  • Extensions to listwise preferences, multi-turn dialogue, and length normalization (frequent practical issues in LLM alignment) are not integrated into the AuxDPO framework.
  • Convergence guarantees for optimizing the empirical AuxDPO loss in non-convex neural policy classes (step-size schedules, trust regions, regularization) are absent.

Empirical evaluation and robustness

  • A comprehensive empirical comparison with strong direct-alignment baselines (e.g., IPO, SimPO, contrastive methods), across diverse tasks and metrics, is not reported.
  • Sensitivity analyses for key hyperparameters (β\beta, λ\lambda), and for varying preference count distributions ns,a,a′n_{s,a,a'}, are missing.
  • Compute and sample-efficiency trade-offs (vs. DPO and two-stage RLHF), including wall-clock time, memory overhead (from δ\delta), and throughput, are not quantified.
  • Robustness to noisy or biased preferences (multi-annotator settings, adversarial or low-quality data) is not evaluated; effects on AuxDPO’s null-space augmentation are unknown.
  • Safety-related metrics (reward hacking, toxicity, hallucination), and whether the added degrees of freedom introduce new failure modes, are not assessed.
  • Statistical significance, error bars, and ablation studies (e.g., removing δ\delta, varying the penalty, re-estimating Aρ,θ0A_{\rho,\theta_0}) are not detailed.

Broader open directions

  • Design of data collection or reweighting strategies that provably mitigate DPO’s sensitivity to preference frequencies in parametric policy classes is open.
  • Necessary and sufficient conditions (beyond global coverage) for DPO to succeed under misspecification have not been characterized.
  • Incorporating learned reward model uncertainty (when r∗r^* is not known and must be estimated) into AuxDPO, and analyzing its effect on the null-space augmentation, remains open.
  • Generalization bounds and sample complexity for AuxDPO (population-to-empirical loss, with Monte Carlo null-space penalties) are not provided.
  • Handling distribution shift in ρ\rho (training vs. evaluation prompts) and adapting Aρ,θ0A_{\rho,\theta_0} accordingly is not discussed.
  • Strategies to control the size of N(Aρ,θ0)\mathcal{N}(A_{\rho,\theta_0}) (when the null-space is large) to avoid degenerate or uninformative solutions while retaining alignment benefits are not developed.
Ai Sparkles Streamline Icon: https://streamlinehq.com View Paper Prompt List Streamline Icon: https://streamlinehq.com View All Prompts
Ai Generate Text Spark Streamline Icon: https://streamlinehq.com

Practical Applications

Immediate Applications

The following applications can be adopted now by practitioners to improve preference-based alignment workflows and downstream deployments.

  • AuxDPO-based upgrade to LLM alignment pipelines (software/AI)
    • Use case: Replace standard DPO loss with AuxDPO to reduce misspecification-driven failures (preference reversal, reward reduction) while avoiding full two-stage RLHF.
    • Workflow: Modify the training loss to include auxiliary “delta” variables and a null-space penalty term; keep the single-phase supervised training loop. Integrate into common libraries (e.g., TRL-style fine-tuning) by computing base-policy log-probability gradients and adding the penalty that enforces δ ∈ N(A_{ρ,θ₀}).
    • Tools/products: A “drop-in” AuxDPO loss module for LLM fine-tuning; configuration templates for λ (penalty weight) and β (KL regularization).
    • Assumptions/dependencies: Access to base policy gradients; pairwise preference datasets (BTL-like or binarized); operation chiefly in the large-β (local) regime; modest hyperparameter tuning.
  • Preference data curation and weighting strategy to reduce DPO sensitivity (data operations across sectors)
    • Use case: Proactively rebalance pairwise comparison counts n_{s,a,a′} to reduce DPO’s sensitivity to sampling frequencies and mitigate failure modes if DPO must be used.
    • Workflow: Instrument preference collection to track per-pair counts, add sampling quotas or stratification, and/or reweight loss terms to counter imbalances.
    • Tools/products: Data dashboards that monitor pairwise coverage; utilities that rebalance or reweight preference pairs.
    • Assumptions/dependencies: Availability of logging for pair count frequencies; alignment goals consistent with BTL-style pairwise comparisons.
  • Alignment quality assurance and monitoring (software safety/ML ops)
    • Use case: Add diagnostics for misspecification to training and evaluation: check for preference order reversal, likelihood displacement of chosen responses, and expected reward drop relative to base policy.
    • Workflow: Post-train probes comparing base vs aligned policy probabilities; synthetic pairwise tests; alerting thresholds.
    • Tools/products: QA harness and audit reports; risk indicators (reward-change score, preference-consistency score).
    • Assumptions/dependencies: Either approximate reward proxies, human labels, or a reliable offline evaluator; evaluation datasets representative of deployment domain.
  • Cost-aware alignment for small labs and startups (academia/open-source/SMBs)
    • Use case: Achieve RLHF-like behavior without the compute and engineering burden of training a separate reward model and on-policy rollouts; AuxDPO enables single-phase tuning.
    • Workflow: Fine-tune SFT models (reference policy) directly with AuxDPO; leverage existing binarized preference datasets (e.g., UltraFeedback variants).
    • Tools/products: Lightweight alignment recipes for 7B–13B models using AuxDPO; cloud templates for low-budget training runs.
    • Assumptions/dependencies: Preference data availability; base policy gradient access; modest hyperparameter selection for the nullspace penalty.
  • Compliance-oriented fine-tuning for regulated sectors (healthcare, finance, government, legal)
    • Use case: Reduce misaligned or unsafe outputs by adopting an alignment method that matches RLHF local behavior more reliably than DPO, while remaining computationally feasible.
    • Workflow: Implement AuxDPO in domain fine-tuning (policy response style, safety disclaimers, instruction adherence); add misspecification diagnostics to governance checklists.
    • Tools/products: “Compliance-ready” AuxDPO finetune presets; audit artifacts showing reduced risk of preference reversal and reward reduction.
    • Assumptions/dependencies: Domain-specific preference datasets curated to regulatory requirements; human review for safety-critical workflows.
  • Preference-based optimization beyond LLMs (bandits/recommendation)
    • Use case: Apply AuxDPO’s nullspace-augmented projection to parametric bandit/recommender policies trained from pairwise feedback (A/B preferences, click data).
    • Workflow: Build policy scoring functions that incorporate AuxDPO-like auxiliary variables to match the local natural-gradient target; use in rankers or selectors.
    • Tools/products: Loss components for pairwise ranking that align better with desired preference order; evaluation in offline A/B simulations.
    • Assumptions/dependencies: Differentiable parametric policy; gradient access; pairwise preference logs; local updates near a reference policy.

Long-Term Applications

These applications require further research, scaling, or productization before broad deployment.

  • Full-featured AuxDPO library and ecosystem (software/AI tooling)
    • Use case: An open-source alignment toolkit that implements AuxDPO at scale (token-level sequence models, efficient gradient plumbing, automatic λ tuning).
    • Workflow: End-to-end pipelines with dataset curation, training, and evaluation; integration with major frameworks; robust defaults and safety checks.
    • Dependencies: Engineering for large action spaces; fast nullspace penalty estimation; community validation across diverse tasks.
  • Extension to multimodal and robotics preference alignment (vision-language agents, embodied systems)
    • Use case: Robust preference alignment for policies with image/video inputs or continuous action spaces; reduce misspecification in human-in-the-loop control.
    • Workflow: Adapt AuxDPO’s geometric approach to temporal RL settings; design δ for sequence or trajectory spaces; combine with on-policy updates if needed.
    • Dependencies: Differentiable multimodal/robotic policies; preference datasets for interactive tasks; new theory beyond large-β and single-step settings.
  • Active preference sampling to minimize projection bias (data collection science)
    • Use case: Automatically select informative pairs to reduce weighted reverse-KL projection artifacts; improve identifiability of preferred policies.
    • Workflow: Query strategies that target underrepresented pairs; closed-loop data curation (active learning) for alignment.
    • Dependencies: Online sampling infrastructure; theoretical criteria for informativeness; simulators or human-in-the-loop annotation.
  • Standards and audits for misspecification-aware alignment (policy/regulation)
    • Use case: Alignment guidelines and certifications recognizing DPO misspecification; recommend AuxDPO/RLHF or equivalent mitigations for safety-critical applications.
    • Workflow: Benchmark protocols (preference reversal checks, reward drop prevention), reporting formats, and audit trails.
    • Dependencies: Multi-stakeholder consensus; domain-specific metrics; regulatory acceptance.
  • Adaptive method selection and meta-alignment pipelines (MLOps/AutoML)
    • Use case: Automatically choose between RLHF, AuxDPO, or standard DPO based on model capacity, data coverage, β regime, and deployment risk profile.
    • Workflow: Preflight diagnostics (rank-nullity checks, curvature estimates), then route to the appropriate alignment method; monitor and switch as data shifts.
    • Dependencies: Reliable model geometry estimators; meta-learning tying method choice to outcomes; longitudinal tracking.
  • Theory and algorithms beyond the large-β regime (academia)
    • Use case: Generalize geometric insights to moderate/low β, nonlocal moves, sequence-level losses, and realistic human preference noise.
    • Workflow: Develop refined equivalence classes, non-linear projections, and new direct-alignment variants that maintain RLHF guarantees without rollouts.
    • Dependencies: New mathematical tools; empirical validation across complex tasks; scalable implementations.
  • Enterprise “Alignment-as-a-Service” (industry)
    • Use case: Managed cloud service that delivers domain-specific AuxDPO-based fine-tuning with governance, privacy, and evidence reports.
    • Workflow: Secure data ingestion, automatic AuxDPO tuning, compliance-grade logging, and post-deployment monitoring.
    • Dependencies: Data security practices; sector integrations (healthcare EHR, finance KYC); performance SLAs.
  • Reward manifold visualization and diagnostics (developer experience)
    • Use case: Tools to visualize implicit reward manifolds and nullspaces; help engineers spot misspecification risks and adjust training/data accordingly.
    • Workflow: Dashboards that plot local geometry, pairwise coverage, and movement from base policy; “what-if” simulations for pair count reweighting.
    • Dependencies: Efficient geometry approximations; UX for large models; alignment of visual indicators with actual deployment metrics.
Ai Sparkles Streamline Icon: https://streamlinehq.com View Paper Prompt List Streamline Icon: https://streamlinehq.com View All Prompts
Ai Generate Text Spark Streamline Icon: https://streamlinehq.com

Glossary

  • AuxDPO: A modified DPO algorithm that adds auxiliary variables to correct misspecification and better match the RLHF solution. "we propose AuxDPO, which introduces additional auxiliary variables in the DPO loss function to help move towards the RLHF solution in a principled manner and mitigate the misspecification in DPO."
  • Bradley–Terry–Luce (BTL) model: A probabilistic model for pairwise preferences where the preference probability is a logistic function of reward differences. "the preference ordering between a pair of responses is assumed to be sampled according to a Bradley–Terry–Luce (BTL) model: the probability of a being preferred to a' is given by p_{s,a,a'}{\BTL}(r*) = \sigma!\left(r*(s,a)- r*(s,a') \right)"
  • Coverage condition (global coverage): An assumption bounding policy probability ratios to guarantee sufficient support for learning and convergence. "argued that a global coverage condition max⁡s,aπθ(a∣s)πθ0(a∣s)≤C\max_{s, a} \frac{\pi_\theta(a\mid s)}{\pi_{\theta_0}(a \mid s)} \leq C for all $\theta \in \Real^d$ is necessary for DPO to converge to the optimal policy"
  • Direct Preference Optimization (DPO): A direct alignment approach that optimizes a supervised loss derived from a KL-regularized RL objective, bypassing explicit reward model training. "Direct alignment algorithms such as Direct Preference Optimization (DPO) fine-tune models based on preference data"
  • Empirical DPO loss: The finite-sample supervised loss minimized by DPO over observed preference pairs. "Given the dataset $\cD$, DPO \citep{rafailov2023direct} finds the minimizer of the {\em empirical} DPO loss"
  • Equivalence classes (of reward functions): Sets of rewards that induce the same local RLHF-optimal policy under the natural gradient relation. "it partitions the set of all reward functions into equivalence classes as follows."
  • Fisher information matrix: The expected outer product of score functions; defines the natural metric for gradient steps in policy space. "$F_{\rho,\theta_0}= \mathbb{E}_{\rho,\pi_{\theta_0}\left[\nabla \log\pi_{\theta_0}(a|s) \nabla \log \pi_{\theta_0}(a|s)^\top\right]$ denotes the Fisher information matrix at πθ0\pi_{\theta_0}"
  • KL neighborhood: The set of policies within a small KL divergence ball around a base policy. "a policy not in the KL neighborhood of the base policy"
  • KL penalty: A regularization term penalizing deviation from a reference policy via KL divergence in the objective. "and the KL penalty using a second-order Taylor series expansion"
  • Kullback–Leibler (KL) divergence: An information-theoretic measure of dissimilarity between probability distributions. "where $d_\KL(p||q)$ denotes the KL divergence b/w two Bernoulli random variables with parameters p,qp,q."
  • KL-regularized objective: An RL objective augmented with a KL term to keep the policy close to a reference policy. "optimizes a KL-regularized objective of the form $\max_{\pi}\; \mathbb{E}_{s \sim \rho,\, a \sim \pi(\cdot\mid s)}\!\big[r_\phi(s,a)\big]\;-\;\beta\,D_\KL\!\big(\pi(\cdot\mid s)\,\|\,\pi_{\mathrm{ref}(\cdot\mid s)\big)$"
  • Latent reward model: An unobserved reward function assumed to generate preference labels, used as the target for alignment. "align with a latent reward model that generated those preferences."
  • Likelihood displacement: A failure mode where an optimization step unintentionally lowers the likelihood of preferred responses relative to the base. "likelihood displacement, where the probability of preferred responses can drop relative to the base policy"
  • Mahalanobis norm: A norm weighted by a positive semidefinite matrix that measures distance accounting for feature covariance. "the minimum Mahalonobis-norm ∥r∥Dρ,θ0\|r\|_{D_{\rho,\theta_0}}"
  • Manifold (implicit reward manifold): The lower-dimensional set of reward functions implicitly realizable by a given parametric policy class. "the manifold of reward functions implicitly expressed by the policy class"
  • Misspecified estimation: An estimation setup where the true data-generating process lies outside the assumed model class, leading to biased projections. "DPO essentially solves a misspecified statistical estimation problem in the space of reward functions"
  • Natural gradient: A geometry-aware gradient that uses the Fisher metric to produce invariant and efficient policy updates. "relate it to a natural gradient step in policy space."
  • Null space: The set of vectors mapped to zero by a linear operator; used here to introduce additional reward-space degrees of freedom. "along the null space of a base-policy dependent matrix"
  • On-policy: A learning regime where data are collected by the current policy being optimized. "This stage is on-policy and rollout-heavy"
  • Partition function: The normalizing constant that ensures probabilities sum to one in exponential family models. "$Z^*(s)= \sum_{a\in \cA}\pi_{\theta_0}(a|s)\exp(r^*(s,a)/\beta)$ is the normalizing or partition function"
  • Population DPO loss: The expected DPO objective under the true data-generating distribution, as opposed to its empirical approximation. "yielding the {\em population} DPO loss"
  • Preference reversal: A pathology where the learned model inverts the true ordering of preferences. "preference order reversal"
  • Proximal Policy Optimization (PPO): A policy gradient algorithm using clipping or KL constraints to stabilize updates. "typically implemented with PPO-style updates."
  • Reference policy: The fixed baseline policy relative to which KL regularization is applied during alignment. "maintain a stable KL to the reference policy $\pi_{\mathrm{ref}$ (often the SFT model)"
  • Reinforcement Learning with Human Feedback (RLHF): A two-stage alignment pipeline: learn a reward model from preferences, then optimize the policy against it. "Two-stage RLHF is the standard way of carrying out preference-based alignment"
  • Reverse-KL projection: Projecting the true reward-induced preference distribution onto the model class by minimizing reverse KL divergence. "DPO projects (according to reverse-KL divergence weighted by pairwise preference counts ns,a,a′n_{s,a,a'}) the true reward function r∗r^* onto the set of implicit reward functions $\cR^\beta$"
  • Rollout: Generating trajectories or samples from a policy to estimate objectives or advantages during RL. "This stage is on-policy and rollout-heavy"
  • Softmax policy: A policy parameterization where action probabilities are proportional to exponentiated scores. "the neural softmax policy $\pi_\theta(a\mid s) = \frac{\exp(f_\theta(s,a))}{\sum_{a'\in \cA}\exp(f_\theta(s,a'))}$"
  • Supervised Fine-Tuning (SFT): Fine-tuning a base model on labeled instruction-following data; often used as the reference policy. "the reference policy $\pi_{\mathrm{ref}$ (often the SFT model)"
  • Tabular policy class: A non-parametric policy representation with an independent parameter for each state–action probability. "A special case is the tabular policy class, where d=m=∣S∣⋅∣A∣d=m=|S|\cdot|A| and πθ(a∣s)=θs,a\pi_\theta(a|s) =\theta_{s,a}"
  • Variance reduction: Techniques that decrease estimator variance to stabilize and speed up training. "variance reduction, response-length control"
Ai Sparkles Streamline Icon: https://streamlinehq.com View Paper Prompt List Streamline Icon: https://streamlinehq.com View All Prompts
Dice Question Streamline Icon: https://streamlinehq.com

Open Problems

  1. DPO’s ability to output off-KL implicit rewards
List To Do Tasks Checklist Streamline Icon: https://streamlinehq.com

Collections

Sign up for free to add this paper to one or more collections.

User Circle Single Streamline Icon: https://streamlinehq.com Sign Up
X Twitter Logo Streamline Icon: https://streamlinehq.com

Tweets

This paper has been mentioned in 2 tweets and received 294 likes.

Upgrade to Pro to view all of the tweets about this paper:

Start a free 7-day Pro trial