Blackbox Model Provenance via Palimpsestic Membership Inference (2510.19796v1)
Abstract: Suppose Alice trains an open-weight LLM and Bob uses a blackbox derivative of Alice's model to produce text. Can Alice prove that Bob is using her model, either by querying Bob's derivative model (query setting) or from the text alone (observational setting)? We formulate this question as an independence testing problem--in which the null hypothesis is that Bob's model or text is independent of Alice's randomized training run--and investigate it through the lens of palimpsestic memorization in LLMs: models are more likely to memorize data seen later in training, so we can test whether Bob is using Alice's model using test statistics that capture correlation between Bob's model or text and the ordering of training examples in Alice's training run. If Alice has randomly shuffled her training data, then any significant correlation amounts to exactly quantifiable statistical evidence against the null hypothesis, regardless of the composition of Alice's training data. In the query setting, we directly estimate (via prompting) the likelihood Bob's model gives to Alice's training examples and order; we correlate the likelihoods of over 40 fine-tunes of various Pythia and OLMo base models ranging from 1B to 12B parameters with the base model's training data order, achieving a p-value on the order of at most 1e-8 in all but six cases. In the observational setting, we try two approaches based on estimating 1) the likelihood of Bob's text overlapping with spans of Alice's training examples and 2) the likelihood of Bob's text with respect to different versions of Alice's model we obtain by repeating the last phase (e.g., 1%) of her training run on reshuffled data. The second approach can reliably distinguish Bob's text from as little as a few hundred tokens; the first does not involve any retraining but requires many more tokens (several hundred thousand) to achieve high power.
Summary
- The paper introduces a permutation-based statistical test that leverages training order randomness to detect palimpsestic memorization in language models.
- The methodology employs both query and observational strategies, revealing strong correlations in log-likelihoods and n-gram overlaps with p-values as low as 1×10⁻⁸.
- Empirical evaluations across models, from TinyStories to 12B-parameter systems, validate the framework's robustness and its provable control over false positives.
Blackbox Model Provenance via Palimpsestic Membership Inference
Problem Formulation and Motivation
The paper addresses the challenge of establishing the provenance of LLMs and their generated text in a blackbox setting, where only limited access to the model or its outputs is available. Specifically, it considers the scenario where Alice trains a LLM and Bob produces either a derivative model or text using Alice's model, possibly violating terms of service or intellectual property rights. The central question is whether Alice can statistically prove that Bob's artifact (model or text) is derived from her training run, either by querying Bob's model (query setting) or by analyzing Bob's text (observational setting).
The authors formalize this as an independence testing problem, leveraging the inherent randomness in LLM training—particularly the random shuffling of training data. The null hypothesis is that Bob's artifact is independent of Alice's training run. The key insight is that LLMs exhibit palimpsestic memorization: they tend to memorize data seen later in training more strongly, and this memorization is detectable via correlations between model behavior and the order of training examples.
Methodology
Statistical Testing Framework
The core methodology is based on permutation testing. Given Alice's transcript (ordered training data) and Bob's artifact, the authors define test statistics that measure the correlation between the artifact and the training order. Under the null hypothesis (independence), these statistics have a known distribution, enabling exact p-value computation and provable control over false positives.
Algorithmically, the framework involves:
- Subsampling the transcript for computational efficiency.
- Computing a test statistic for the actual transcript and artifact.
- Generating random permutations of the transcript order, recomputing for each, and ranking the observed statistic to obtain a p-value.
Query Setting
In the query setting, Alice can prompt Bob's model and obtain log-likelihoods for her training examples. The primary test statistic is the Spearman rank correlation between the log-likelihoods assigned by Bob's model and the training order. A significant positive correlation indicates that Bob's model memorizes later-seen examples, consistent with derivation from Alice's model.
To increase statistical power, the authors introduce a reference model (independent of Alice's transcript) and compute the correlation of the log-likelihood ratio with training order. This controls for inherent variation in text predictability.
If only token predictions (not probabilities) are available, log-probabilities can be estimated via repeated sampling.
Observational Setting
In the observational setting, Alice only observes text generated by Bob's model. Two approaches are proposed:
- Partitioning: Train n-gram models on contiguous partitions of Alice's ordered training data. For Bob's text, count n-gram overlaps with each partition and correlate these counts with partition order.
- Shuffling: Retrain copies of Alice's model from an intermediate checkpoint on different random shuffles of a subset of the training data. Evaluate the likelihood of Bob's text under the original and retrained models; a higher likelihood under the original ordering is evidence of derivation.
Both approaches yield test statistics whose null distributions can be empirically estimated or approximated, allowing for p-value computation.
Empirical Evaluation
Query Setting Results
Extensive experiments are conducted on Pythia and OLMo model families (1B–12B parameters), as well as custom TinyStories models. The tests are applied to over 40 fine-tuned derivatives, including models subjected to supervised fine-tuning, preference optimization, and model souping.
- Strong numerical results: In all but six cases, p-values are at most , indicating high statistical power.
- Robustness to continued pretraining: Significant correlations persist even after multiple epochs of training on reshuffled data, though the effect size diminishes.
- Model size dependence: Larger models exhibit stronger memorization effects and lower p-values.
- Reference model ablation: Using a reference model closely matched in architecture and training data yields the lowest p-values.
Figure 1: Log-likelihoods of pythia-6.9b-deduped show clear correlation with training order, while independently trained pythia-6.9b does not.
Figure 2: Evaluating a model on its own transcript demonstrates the effectiveness of the query-based test statistic.
Observational Setting Results
The observational tests are more challenging, requiring larger samples of Bob's text for high power.
- Partitioning approach: Several hundred thousand tokens are needed to achieve low p-values, limiting applicability to large-scale text analysis rather than short snippets.
- Shuffling approach: Retraining on as little as 2% of the pretraining data allows detection from a few hundred tokens of Bob's text. Finetuning the test models on Bob's text increases robustness to Bob's own finetuning, but requires more tokens.
Figure 3: Approximate p-values from applying obs to TinyStories models, varying the number of tokens in Bob's text and the amount of retraining/finetuning.
Figure 4: P-values for OLMo-7B are affected by the total number of tokens and the training step at which the sequence occurs.
Figure 5: Sampling from the start of a sequence yields smaller p-values across all sample sizes for OLMo-7B models.
Ablations and Scaling
- Sequence length and position: Sampling longer sequences and from the start of training examples increases test power.
- Model scale: Larger models and more retraining improve robustness to finetuning.
- Sampling temperature: Lower diversity in generated text (low temperature) reduces test effectiveness.
Figure 6: Query test statistic on pythia-6.9b-deduped across checkpoints shows persistent memorization effects.
Figure 7: P-values between order epoch and model epoch for 50k eval samples in TinyStories multi-epoch training.
Figure 8: Varying Bob's sampling temperature and number of total tokens affects p-value sensitivity.
Figure 9: Approximate p-values from obs on TinyStories models, varying retraining and finetuning.
Figure 10: Approximate p-values from obs on TinyStories models, varying Bob's sampling temperature.
Figure 11: Approximate p-values from obs on TinyStories models of different scales, showing improved detection with larger models.
Figure 12: Distribution of obs output under the null, demonstrating conservative p-value behavior.
Theoretical and Practical Implications
The proposed tests provide provable control over false positives via exact p-values, a property lacking in prior heuristic or fingerprinting-based approaches. The methodology is transparent (no private test sets or model modifications required) and noninvasive (no need to alter Alice's model or data).
Contradictory claim: The paper demonstrates that independently trained models on similar data can behave more similarly than actual derivative models, invalidating output-similarity-based heuristics.
From a practical standpoint, the query-based tests are feasible for model providers with API access, while the observational tests are more suitable for large-scale forensic analysis. The computational cost is dominated by the number of queries or retraining required, but subsampling and efficient permutation testing mitigate this.
Limitations and Future Directions
- Data disclosure: The tests require access to Alice's training data, which may be restricted due to copyright or competitive concerns.
- Token/sample complexity: Observational tests require large samples for high power; reducing this is an open problem.
- Compute cost: Retraining models for the shuffling approach is expensive, especially at scale.
- Privacy and copyright: The findings on palimpsestic memorization have implications for privacy leakage and copyright enforcement in LLMs.
Future work should focus on developing more lightweight observational tests, extending the methodology to other modalities, and exploring the privacy implications of order-sensitive memorization.
Conclusion
This paper introduces a rigorous statistical framework for blackbox model provenance via palimpsestic membership inference, leveraging the order-sensitive memorization properties of LLMs. The proposed tests achieve high power, transparency, and noninvasiveness, with strong empirical results across multiple model families and scales. The work advances the state of the art in model and text attribution, with significant implications for intellectual property enforcement, privacy, and the understanding of memorization dynamics in large-scale neural networks.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
A Simple Explanation of “Blackbox Model Provenance via Palimpsestic Membership Inference”
Overview
This paper asks a detective-style question: if Alice trains a LLM, and Bob releases a tool that might secretly be based on Alice’s work, can Alice prove it? The authors show how to do this in two situations:
- When Alice can send prompts to Bob’s model (the “query” setting).
- When Alice only sees text Bob’s model wrote, without touching the model (the “observational” setting).
Their key idea is that models “remember” the order of the data they were trained on—especially the things they saw later in training. This creates a kind of faint “fingerprint” of the training order that Alice can test for.
Key Questions
The paper focuses on two easy-to-understand questions:
- If I trained a model (Alice), can I prove that your model (Bob’s) was built from mine?
- If I only see text your model produced, can I prove that text likely came from a model built from mine?
They want methods that are:
- Effective: works reliably.
- Transparent: doesn’t require secret test sets or hidden tricks.
- Noninvasive: doesn’t force Alice to change how she trains her model (no watermarks or special “canary” strings).
How the Methods Work (with simple analogies)
Think of training a model like writing on a whiteboard over many days. The most recent writing tends to be more visible, even if earlier writing still shows faintly underneath. That layered, partially overwritten effect is called “palimpsestic” (like old parchment re-used for new writing). The model is more likely to “remember” and favor examples seen later in training.
The authors treat the problem like a fairness test: if Bob’s model is unrelated to Alice’s training, then there should be no special connection between Bob’s model (or text) and the exact order Alice saw her training examples. If there is a connection, that’s evidence Bob used Alice’s model.
They measure that connection using correlation and p-values:
- Correlation: measures whether two things rise together. Here, it checks if Bob’s model (or text) “likes” examples more when those examples appeared later in Alice’s training order.
- P-value: a number showing how surprising your result is if there was no real connection. Smaller p-values (like 0.00000001) mean strong evidence.
Query Setting (Alice can prompt Bob’s model)
- What they do: Alice takes her training examples and asks Bob’s model, “How likely is this text?” If Bob’s model really comes from Alice’s, it usually gives higher likelihood to examples that came later in Alice’s training.
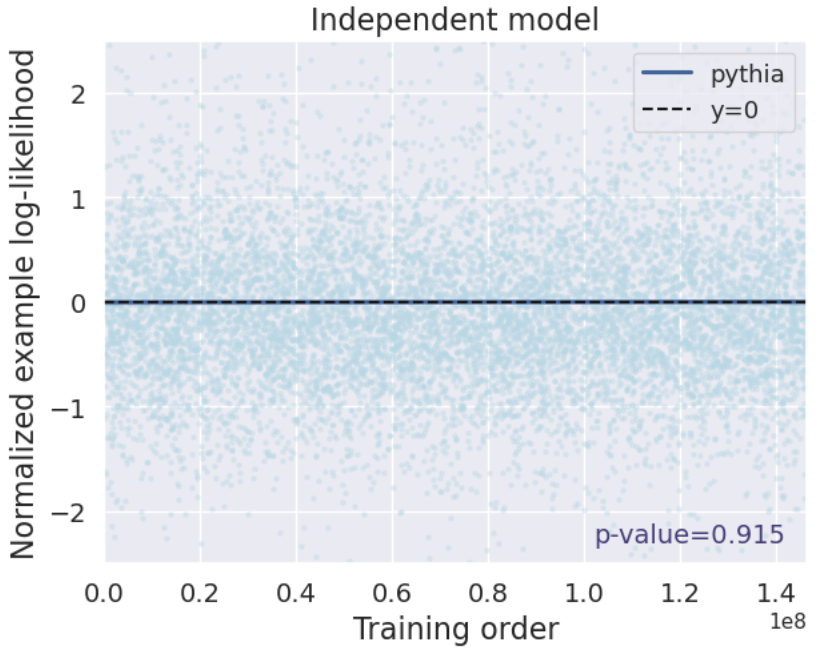
- How they test: They compute a rank correlation between (a) how much Bob’s model likes each training example and (b) that example’s position in Alice’s training order. A strong positive correlation → evidence Bob used Alice’s model.
- Extra trick: They compare Bob’s likelihoods to a separate, independent model’s likelihoods (a “reference” model) to cancel out natural difficulty differences across texts.
Observational Setting (Alice only sees text outputs)
- Challenge: Alice can’t compute Bob’s model’s likelihoods because she can’t query it. So she estimates which parts of Bob’s text look more like things that appear later in Alice’s training.
- Two approaches: 1) Partition approach: Split Alice’s training data into chunks in their original order. Build simple n-gram indices (like a big phrase lookup) for each chunk. If Bob’s text matches phrases more often from later chunks, that’s a sign it came from Alice’s model or a derivative. 2) Shuffle approach: Take a late stage of Alice’s training data and retrain several copies of her model on different shuffled orders of that same data. Then ask: does Bob’s text fit the original (true) order better than the shuffled copies? If yes, that’s evidence of connection. This works because the training order leaves a subtle signature in the model.
Main Findings and Why They Matter
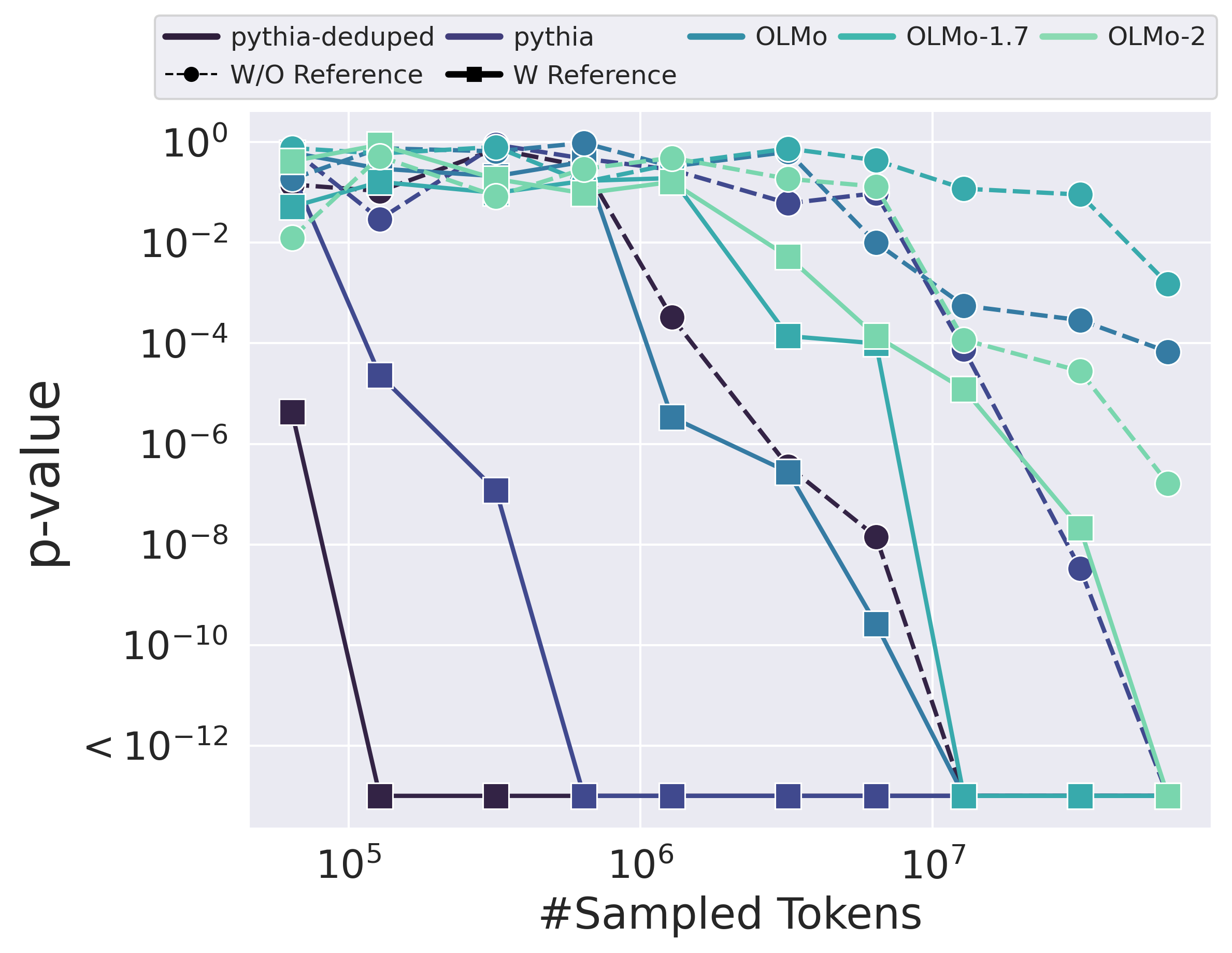
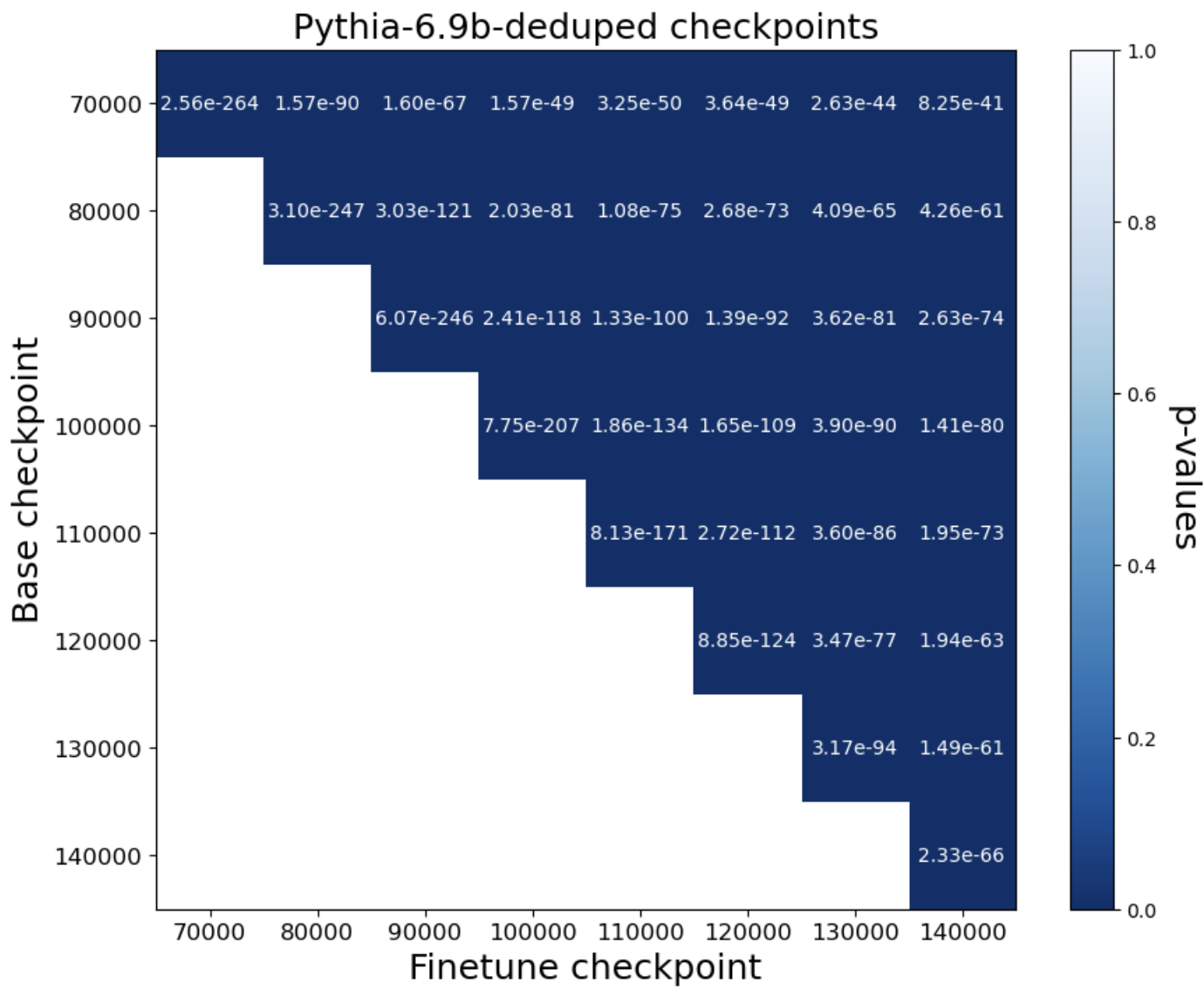
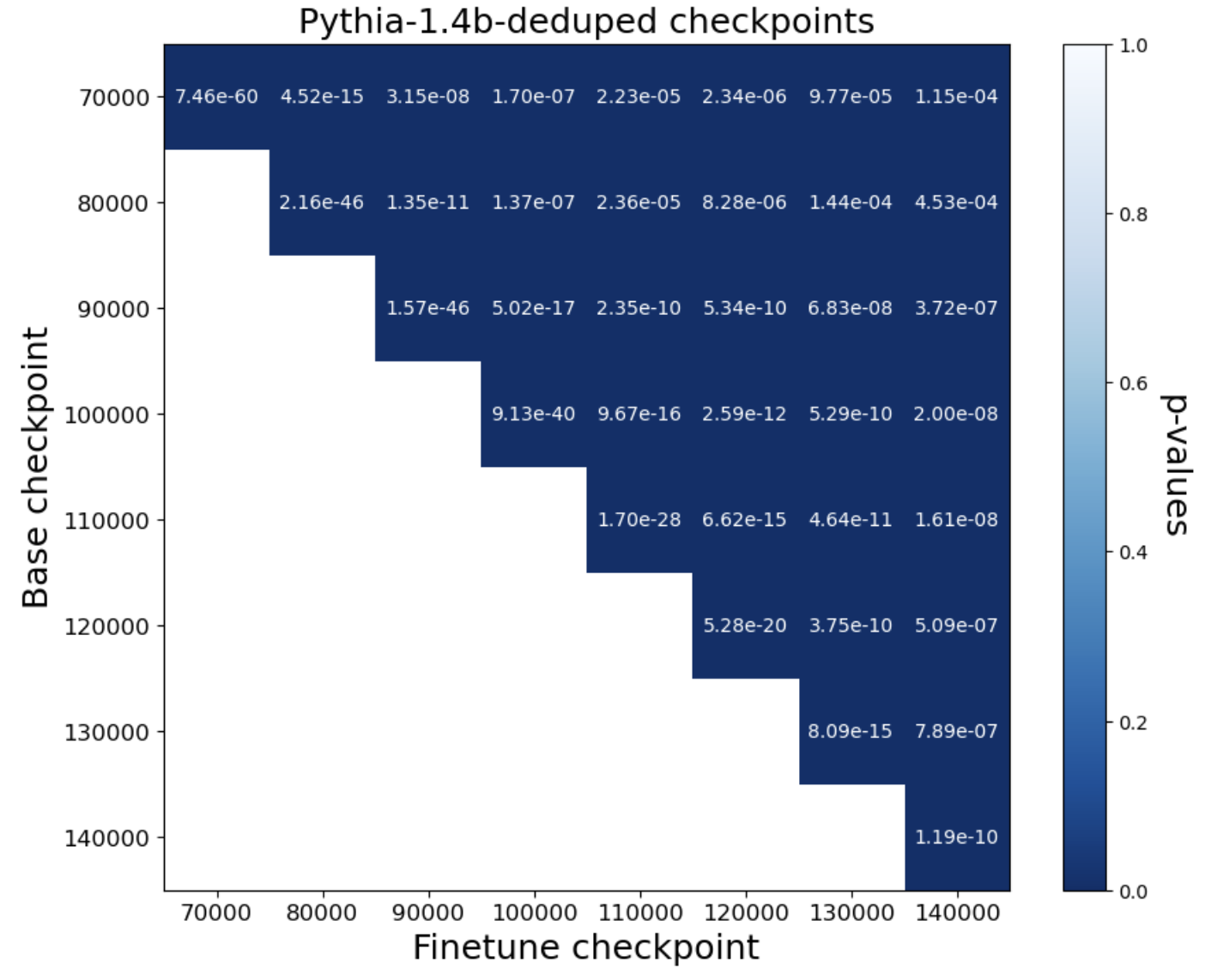
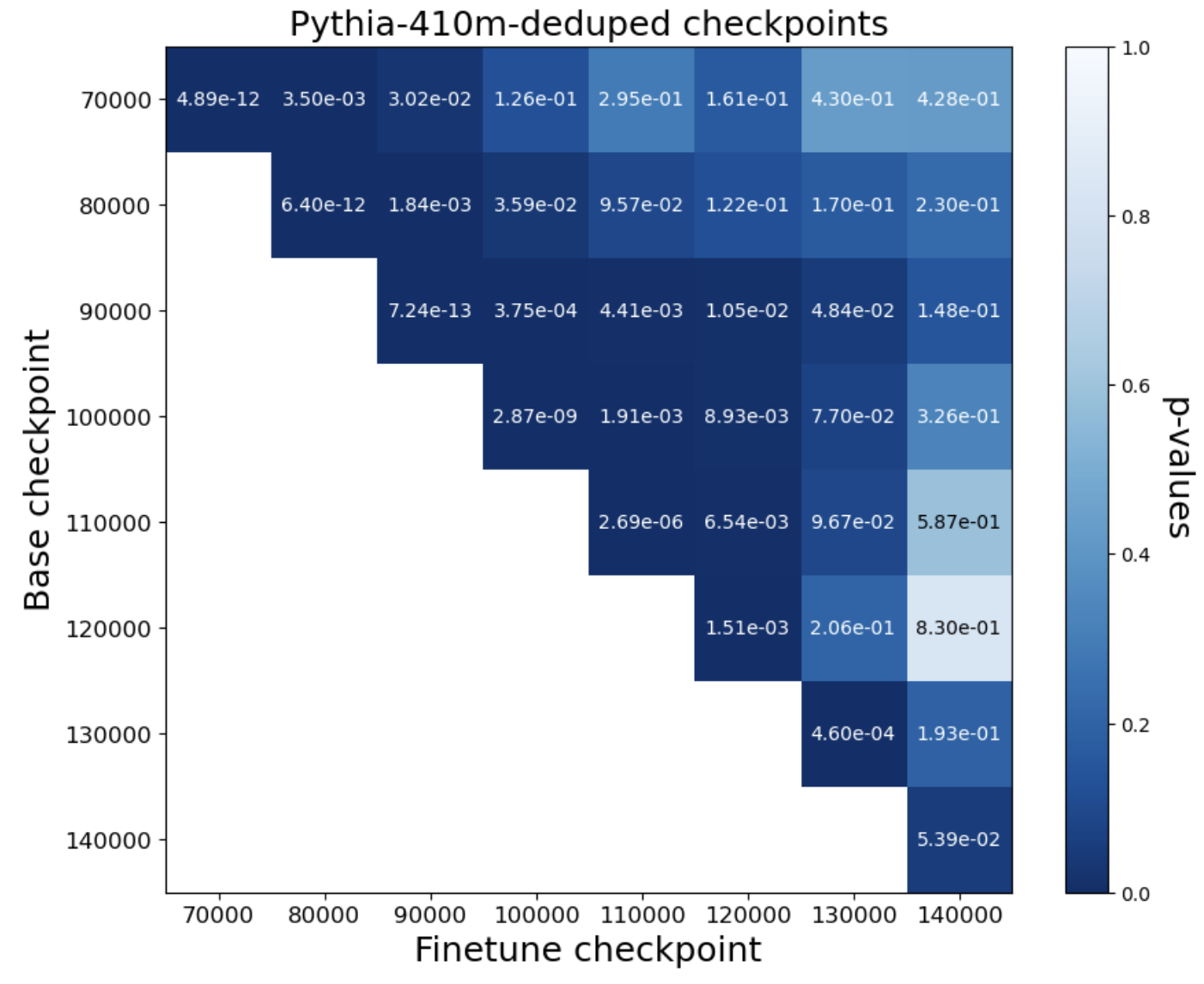
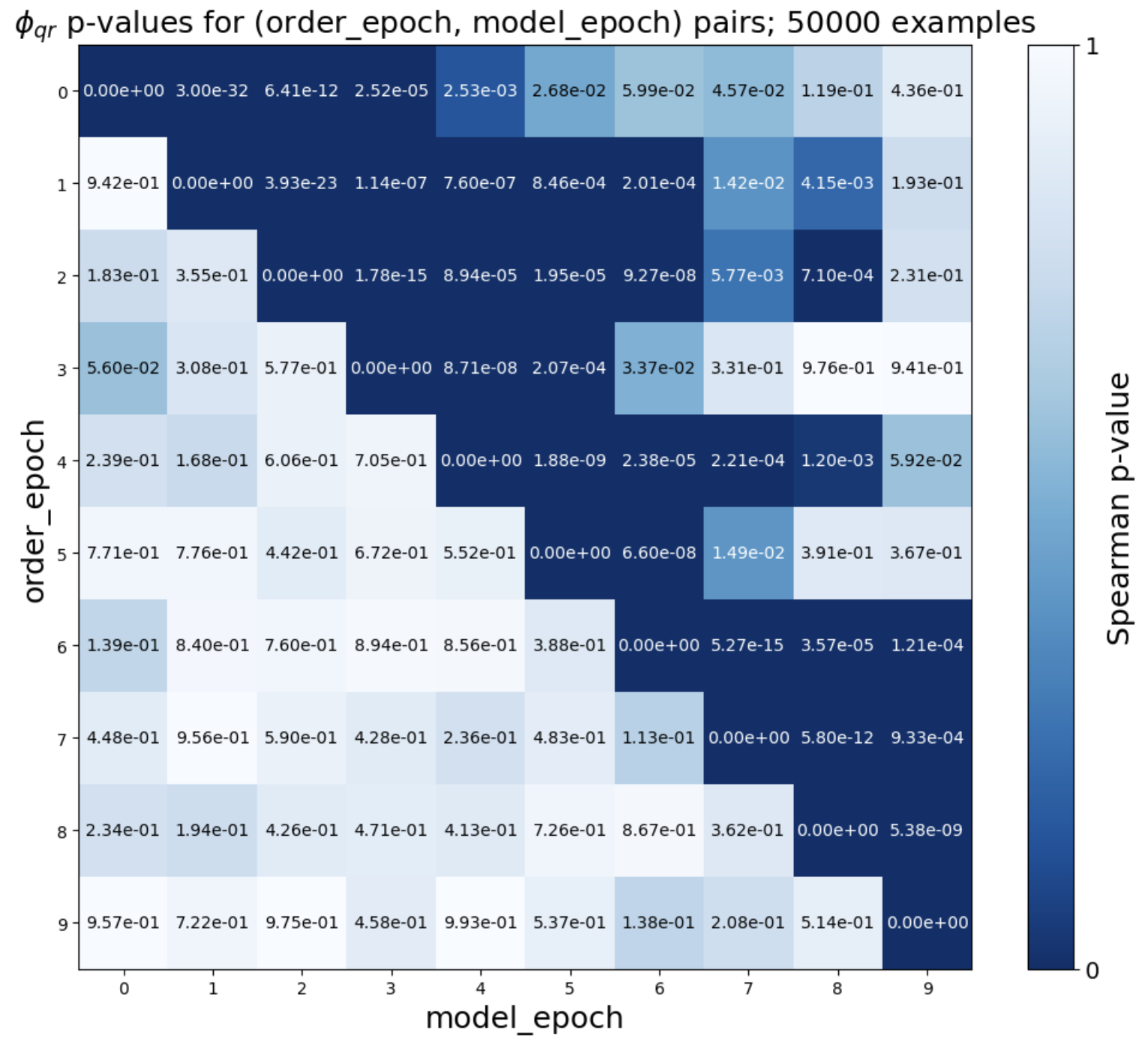
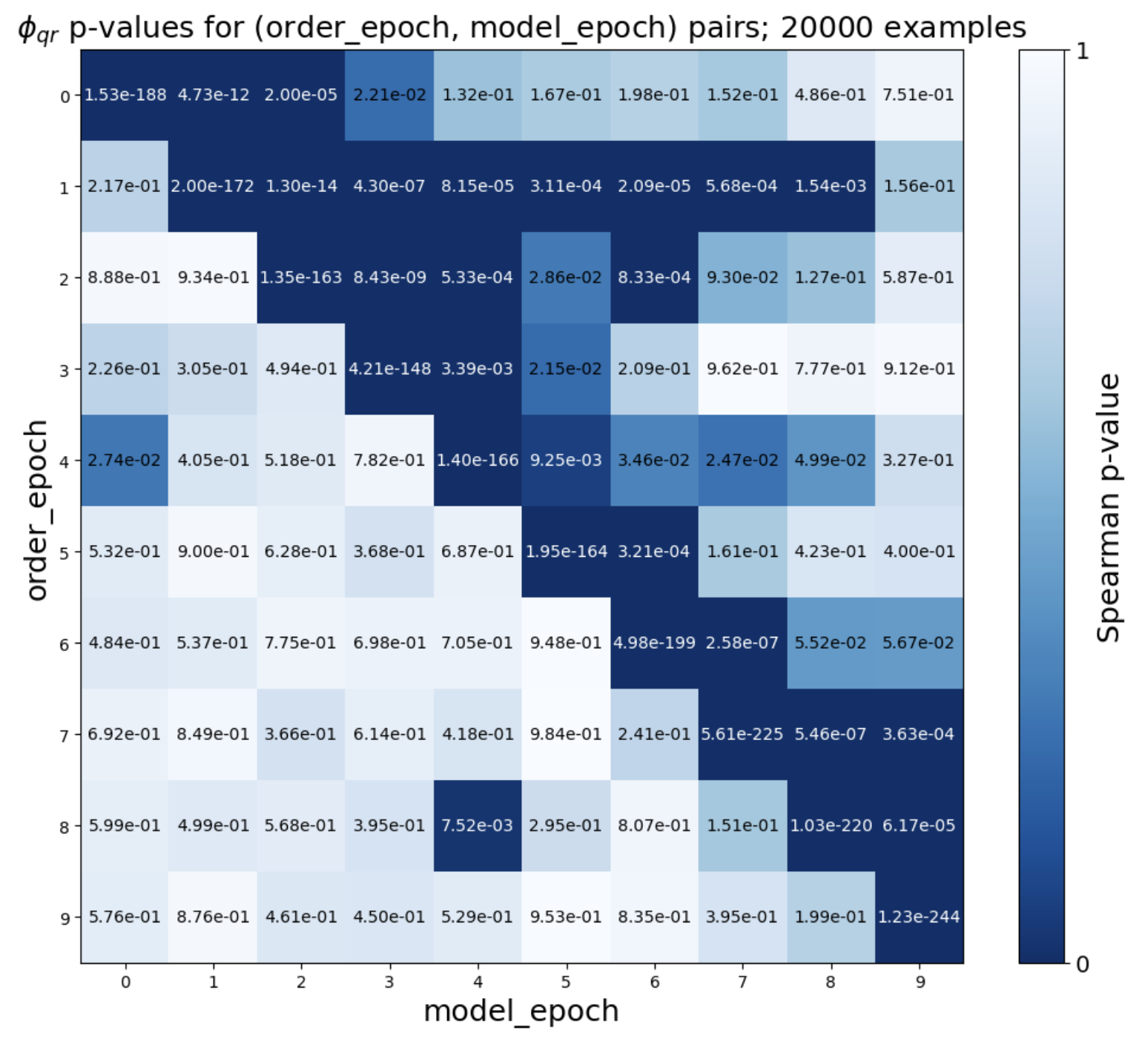
- Query setting: The method works very well. Across more than 40 fine-tuned models (from families like Pythia and OLMo, 1B–12B parameters), the test gave extremely small p-values (often ≤ 10-8). That means very strong evidence that the tested models were derived from the originals. It even works when models are trained for multiple epochs (passes) and when Alice can only estimate probabilities from next-token predictions.
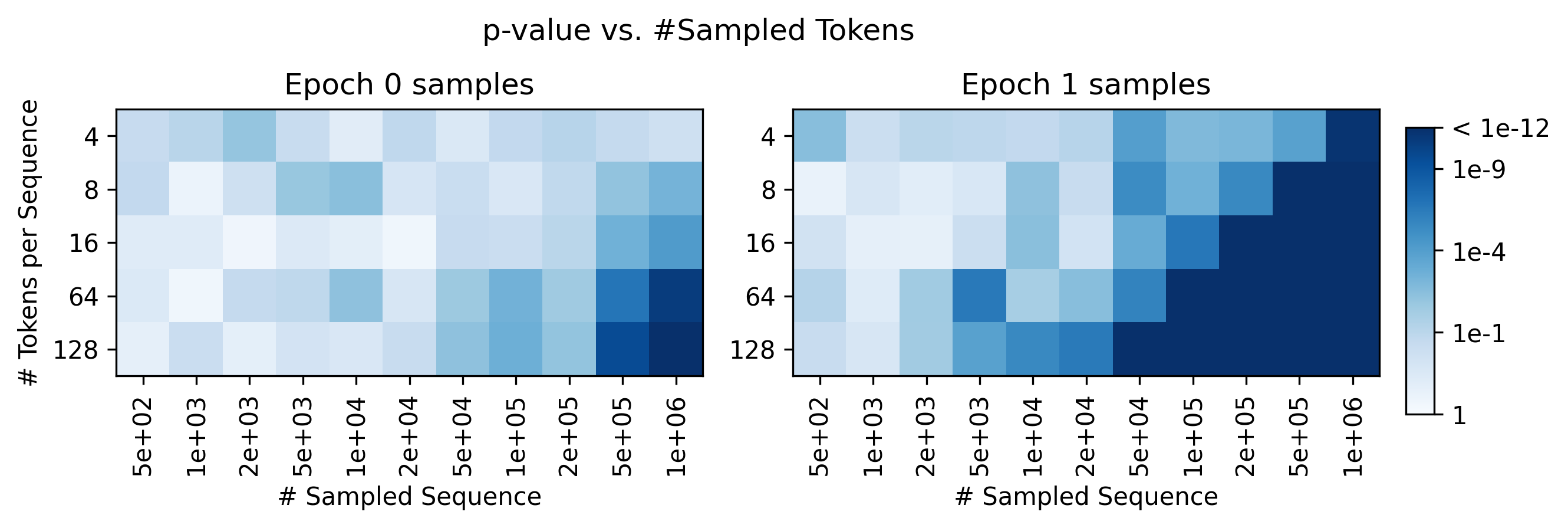
- Observational setting (partition approach): It can work, but it needs a lot of text—often hundreds of thousands to millions of tokens—to be very confident. Good for large-scale analyses (e.g., scanning a platform’s content), less practical for short posts.
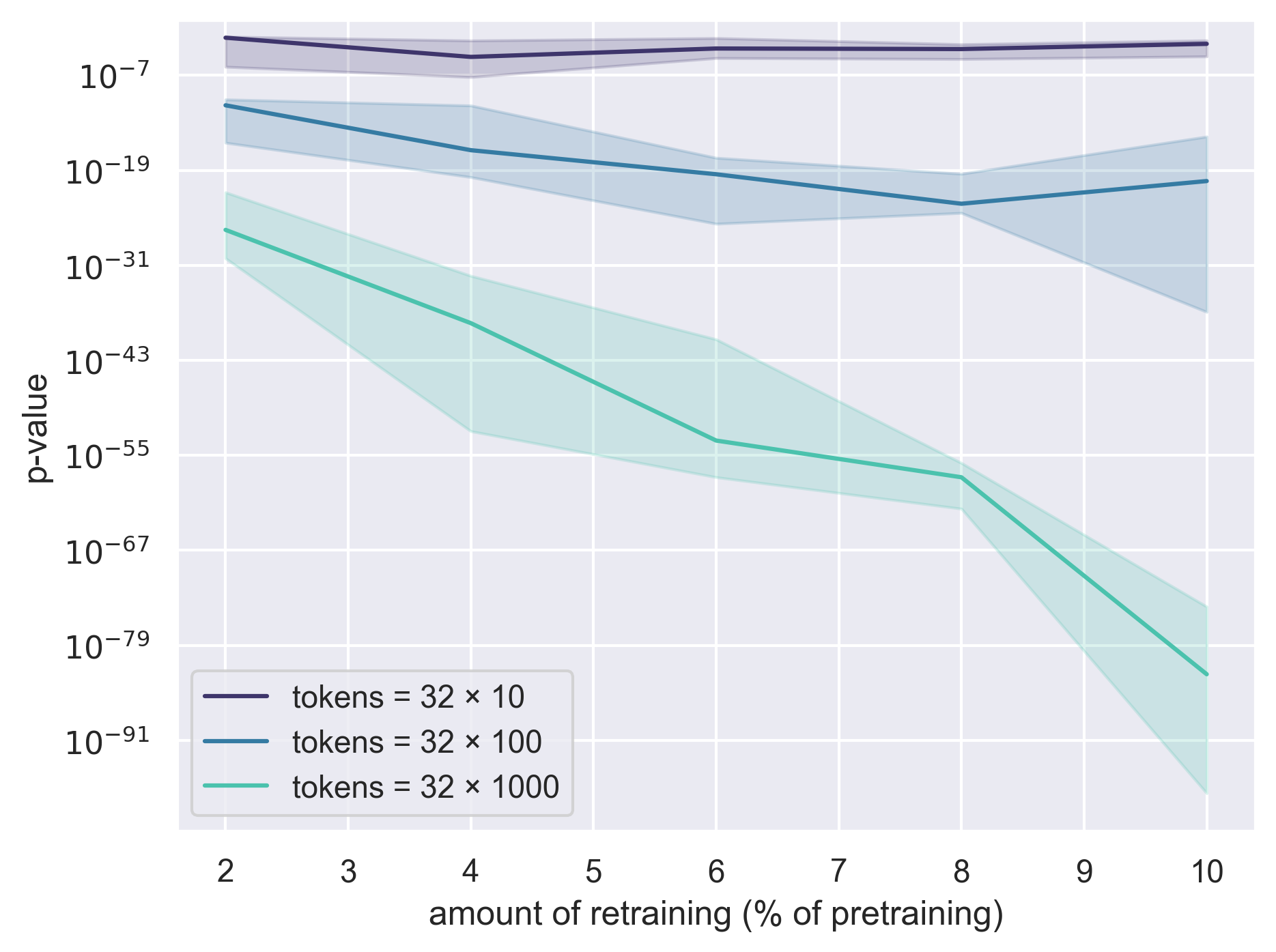
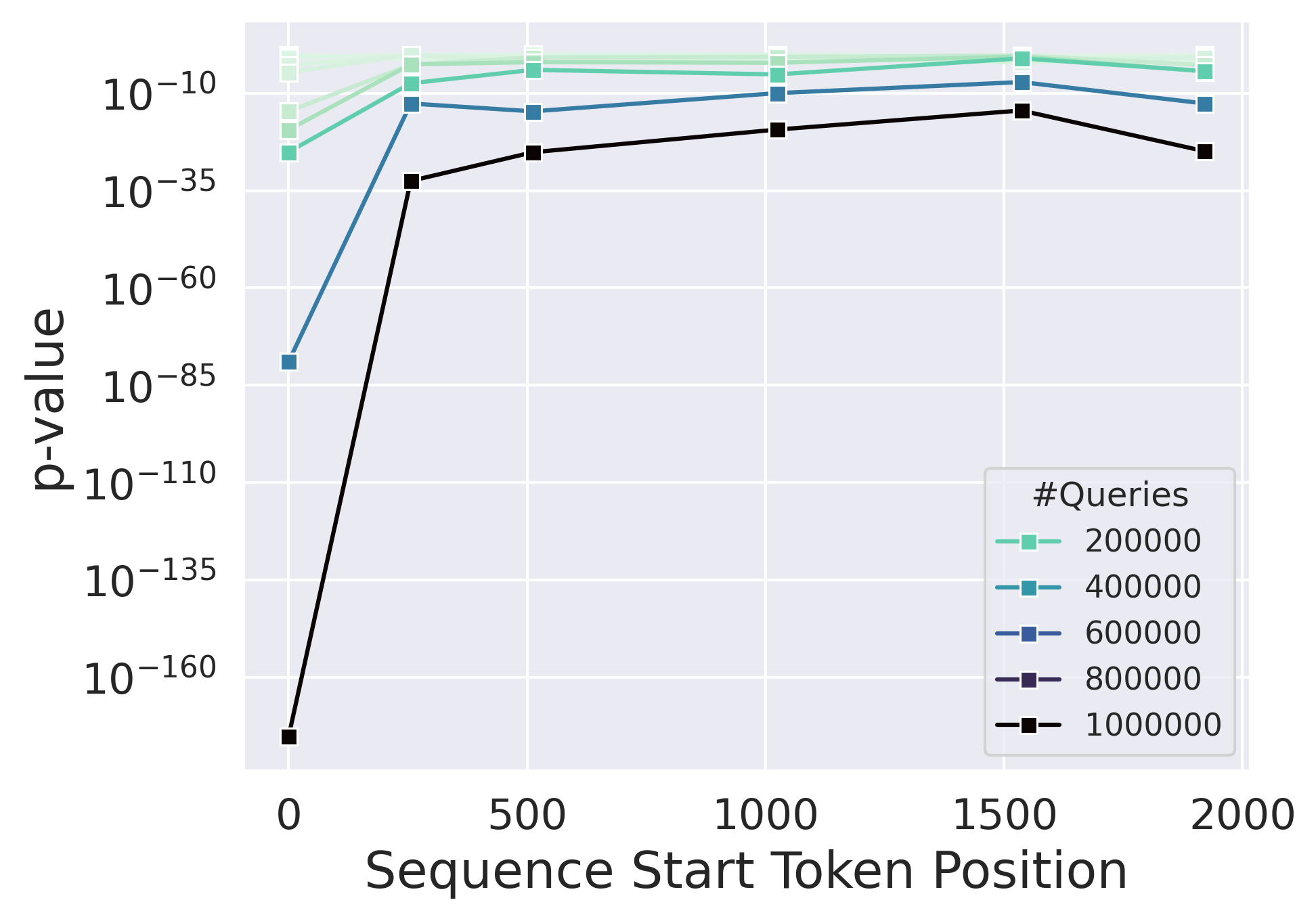
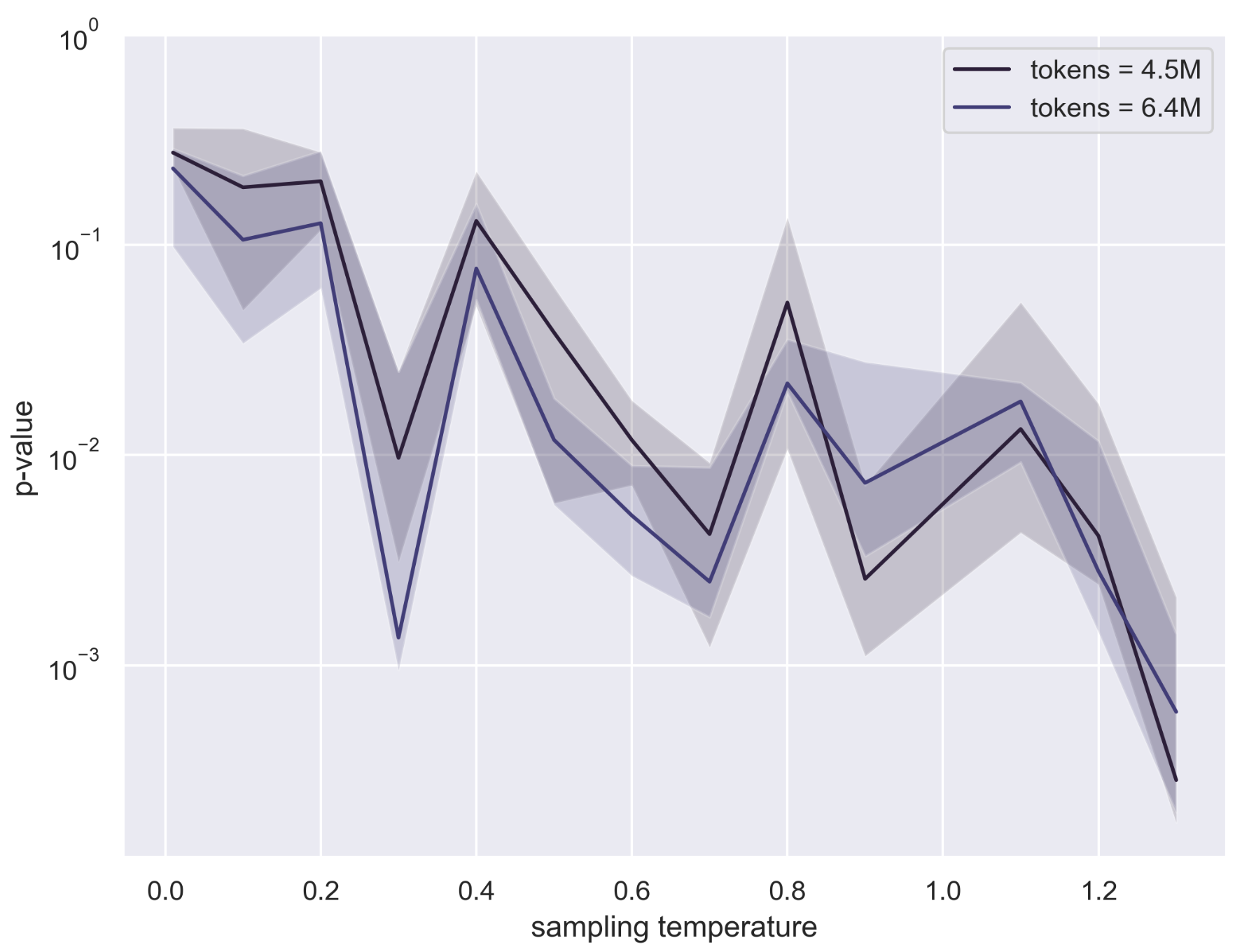
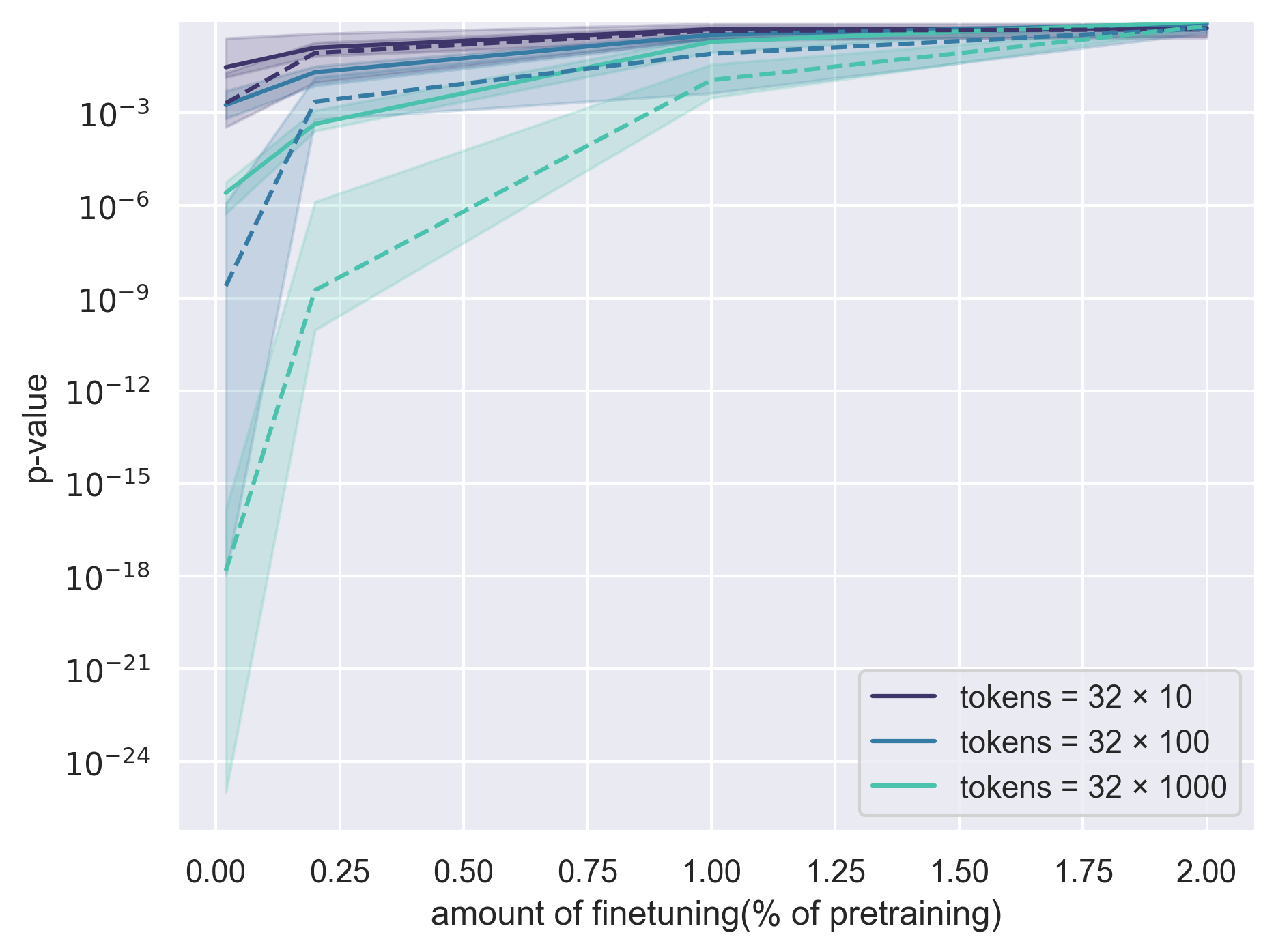
- Observational setting (shuffle approach): Much more sample-efficient. With a small amount of retraining (e.g., repeating just the last ~1% of training using different shuffles), Alice can often tell with only a few hundred to a few thousand tokens whether Bob’s text fits the original model better than the reshuffled copies. This is strong evidence Bob used Alice’s model.
- Overall: The paper offers tests that don’t need hidden data or special watermarks. They rely on a natural property of models: they remember later-seen training examples more.
Implications and Potential Impact
- Practical enforcement: Model creators can check whether others are using their models without permission, supporting fair licensing and attribution.
- Transparency: Because the tests don’t rely on secret test sets, results can be shared and verified publicly if the relevant portion of training order is disclosed.
- Noninvasive: No need to “tamper” with the model (e.g., inserting watermarks). The tests use normal training procedures and simple statistical checks.
- Insights on memorization: The work shows that training order leaves a lasting trace—like layered writing on a palimpsest. That helps us understand how models memorize, forget, and “lean” toward later-seen data. It also raises considerations about privacy and copyright, since parts of the training data may be more likely to be “regurgitated.”
In short, the paper provides a clear, statistically sound way to tell if a model or a piece of text likely came from a specific training run—by reading the “faint handwriting” that training order leaves behind.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a single, concrete list of what remains missing, uncertain, or unexplored, structured to enable actionable follow-up work.
- Assumption of perfectly shuffled training order: How robust are the tests to realistic violations (non-uniform shuffling, dataloader artifacts, weighted mixtures, curriculum, repeated exposures, multi-phase training with non-random ordering)? Develop diagnostics to verify “shuffle quality” and robustness bounds when the assumption fails.
- Dependence on access to the ordered transcript: Many developers do not log or disclose fine-grained training order. What minimum fraction or granularity (e.g., phase-level, dataset-level, batch-level) of the transcript is needed to retain statistical power? Provide sample-complexity guarantees as a function of available order information.
- Statistical calibration of when using rank correlation: The paper uses Spearman rank correlation but converts to p-values via a t-distribution (appropriate for Pearson). Derive and validate exact or asymptotic null distributions for Spearman under the independence hypothesis, or use efficient permutation-based calibration with clear computational trade-offs.
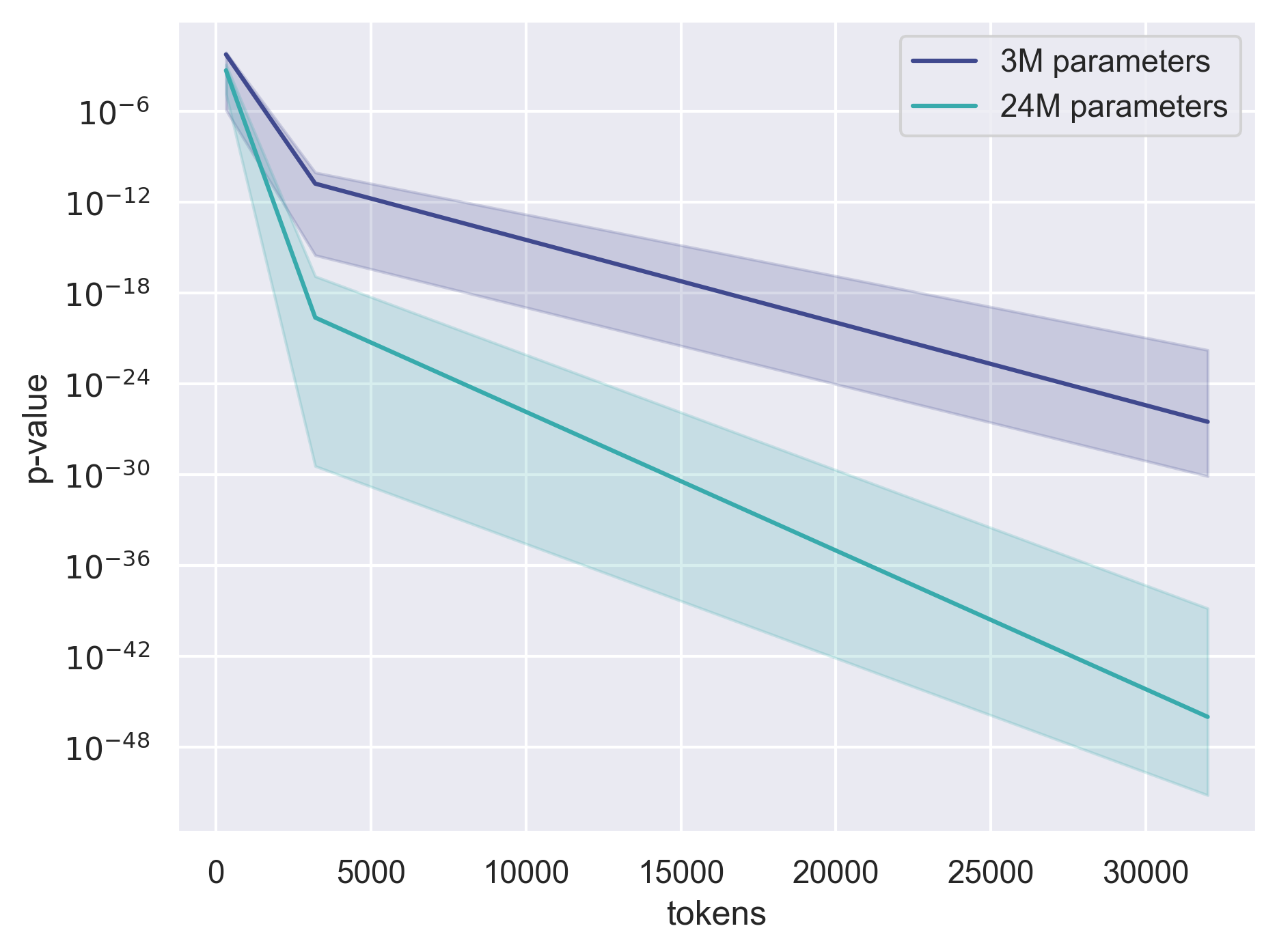
- Power/sample complexity characterization: Provide principled bounds for the number of tokens/queries needed to achieve target power across model scale, dataset diversity, and training length (pretraining and post-training). Current evidence is empirical; formal guarantees are absent.
- Reference model selection: The effectiveness of obsobsobs$ z-scores: The test treats the z-score as approximately normal and validates empirically at small scales. Derive the exact null (or finite-sample approximations) and characterize error when k (number of reshuffles) is small (e.g., k=2–3).
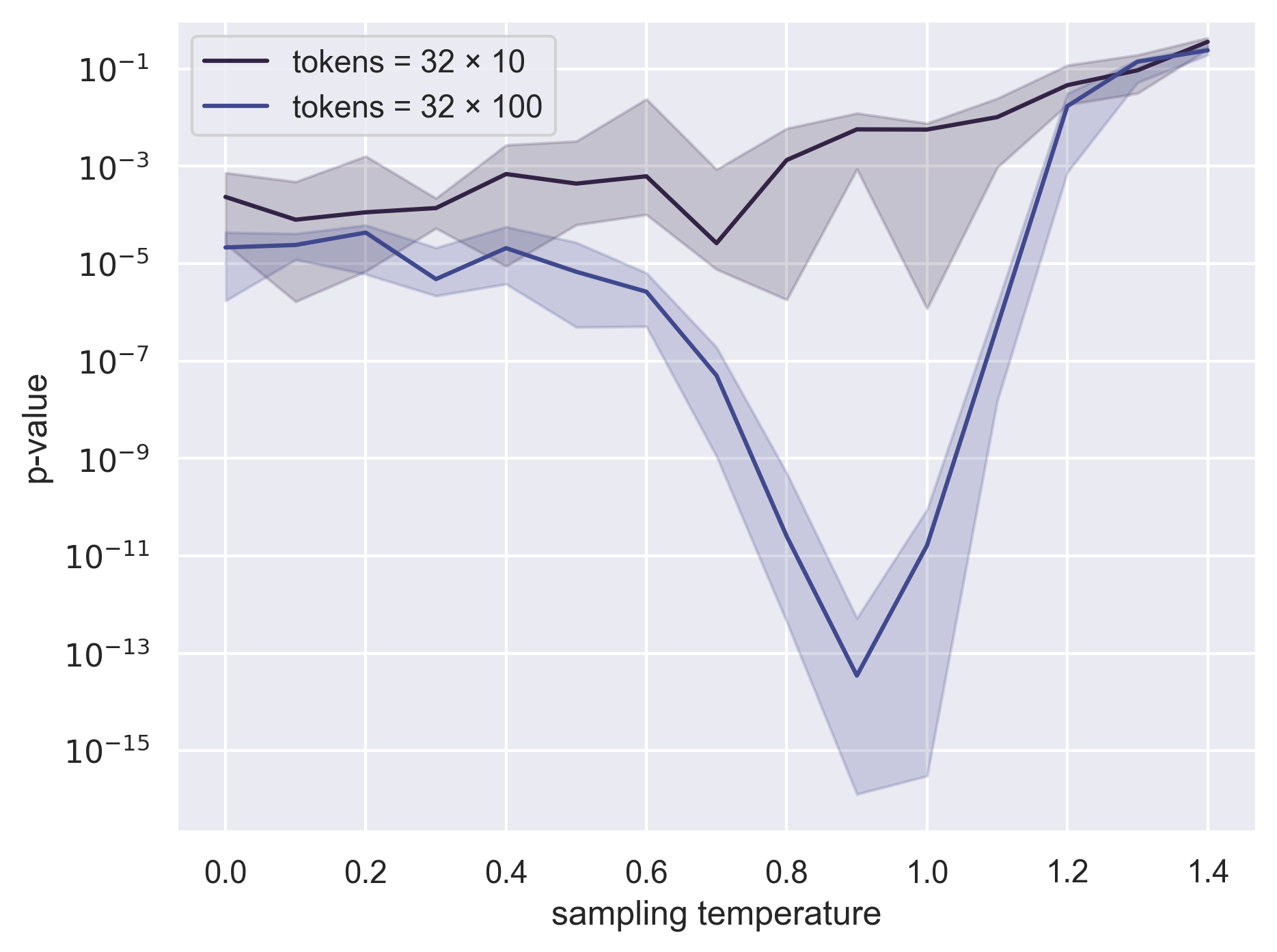
- Robustness to extensive post-training: Systematically map detection power as a function of Bob’s fine-tuning budget, method (SFT, RLHF, DPO, instruction tuning), and data source. Current results show loss of power beyond ~1% fine-tune on TinyStories; quantify thresholds and scaling laws more broadly.
- Evasion strategies and trade-offs: Analyze adversarial tactics (distillation into new architectures, aggressive regularization/anti-memorization, heavy quantization/pruning, MoE gating changes, weight averaging/souping, noise injection) and the corresponding utility degradation needed to evade detection. Provide attack-to-utility Pareto frontiers.
- Generalization beyond tested families: Validate on closed-source families (e.g., Llama, Mistral) and non-English or code-heavy corpora. Assess domain and language transfer: does palimpsestic correlation persist under strong domain shift?
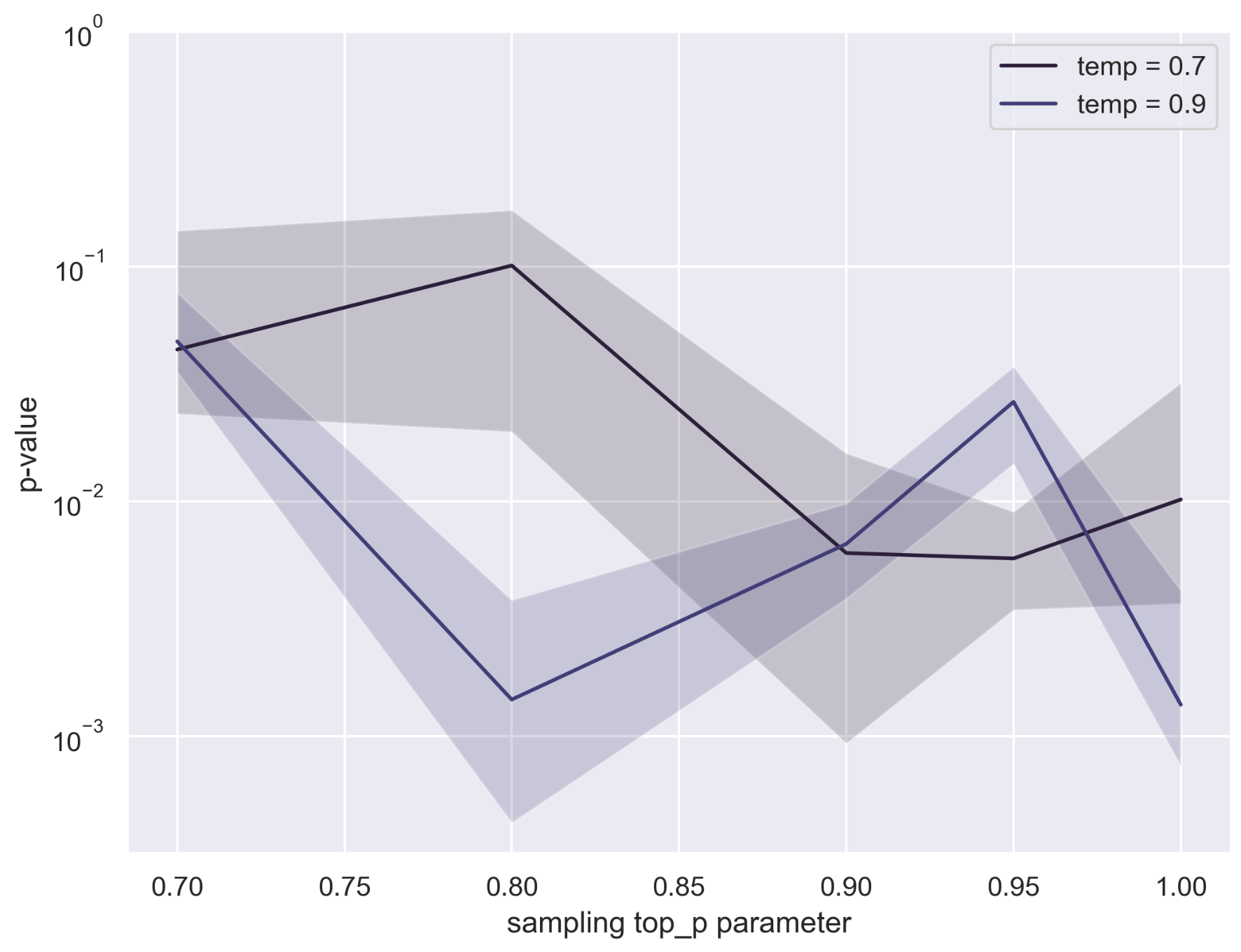
- Sensitivity to generation settings: Observational test power varies with temperature and sampling mode (top-k/p, beam search). Provide systematic correction or robust test statistics that reduce sensitivity to decoding hyperparameters.
- Multi-epoch retention: TinyStories experiments suggest partial retention across many epochs, but results are mixed. Quantify how order information decays with epochs, under repeated reshuffles, and across large-scale runs (billions–trillions of tokens).
- Duplicate and near-duplicate data: How do dataset duplication and near-duplicate clusters affect palimpsestic signals and false attribution risk? Develop de-dup-aware statistics or controls to prevent spurious correlations driven by repeats.
- Shared-data independence: If Bob trains independently on the same corpus with a different shuffle, the artifact is deemed independent under this framework and may not be detectable. Clarify the scope: can the method be extended to infer dataset overlap (dataset inference) without violating transparency/noninvasiveness?
- Scalability of n-gram indexing: The partitioning approach required ~1.4TB for partial Pythia indexing. Explore memory-efficient, streaming, or hashed/sketch-based indices that preserve test validity.
- Practical logging requirements: Define minimal logging standards (batch IDs, seeds, phase boundaries) that allow later provenance testing while minimizing storage and privacy risks. Quantify how logging fidelity impacts test power.
- Legal/forensic calibration: Provide end-to-end error calibration (false positive/negative rates), reproducibility protocols, and chain-of-custody guidance for real-world attribution claims, including multiple-testing corrections across models, datasets, and phases.
- Cross-modality extension: Investigate whether palimpsestic provenance tests extend to other modalities (vision, audio, multimodal LLMs), where training order and memorization dynamics differ.
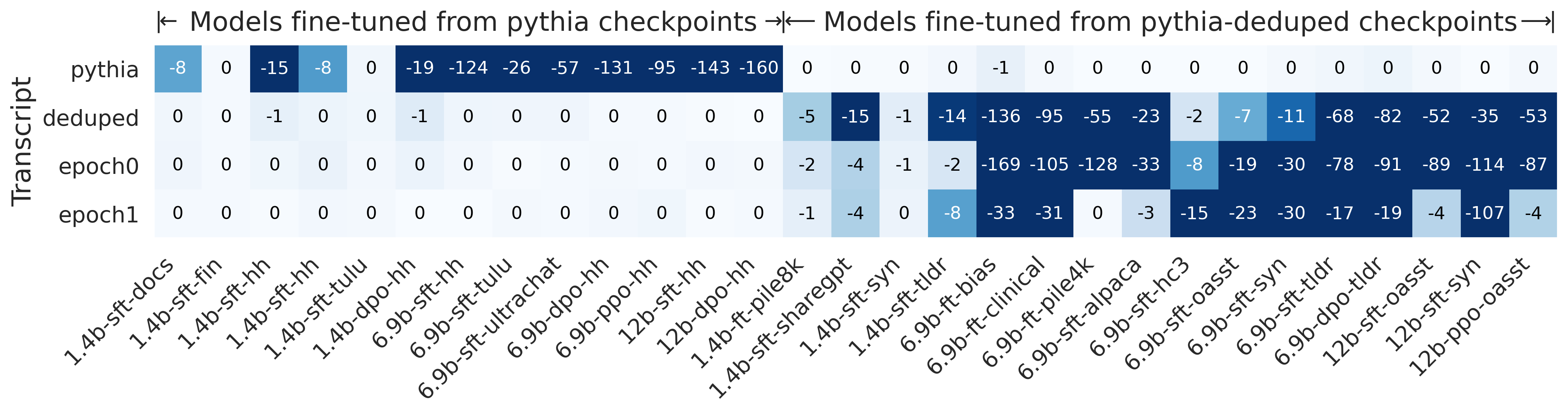
- Open-source reproducibility gaps: Some findings (e.g., suspected misdocumentation of pythia-2.8b-deduped) indicate data/recipe inconsistencies. Establish community benchmarks and audit tools to validate training-order claims and support provenance testing.
Practical Applications
Overview
This paper introduces statistically rigorous, transparent, and noninvasive tests to establish the provenance of LMs and LM-generated text, even when the suspected derivative is only accessible as a blackbox. The core innovation is to frame provenance as an independence testing problem and exploit “palimpsestic memorization” in LMs: later-seen training examples are more likely to be memorized. The proposed tests correlate a suspected model’s or text’s behavior with the known order of training examples in Alice’s training run, yielding exact p-values under standard shuffling assumptions.
Below are practical applications that follow from the paper’s findings and methods. Each item notes sector(s), potential tools/workflows, and key assumptions/dependencies.
Immediate Applications
The following applications can be deployed now with existing open-weight models, basic access to blackbox outputs, and moderate compute.
- License compliance auditing for open-weight models (Industry, Legaltech, Software)
- What: Verify whether a blackbox service or product is built from your open-weight LM without attribution (e.g., “Built with Meta Llama 3”).
- How: Use the query-setting test (Spearman correlation of log-likelihoods vs. training order; exact p-values) to assess dependence on your training transcript.
- Tools/workflows: “Model Provenance Auditor” (library/CLI); automated query harness; p-value reporting.
- Assumptions/dependencies: Access to ordered training transcript (or a shareable subset); the blackbox model must return token probabilities (or allow approximations via prompting); moderate query costs.
- API misuse detection by model providers (Industry, Software/AI platforms)
- What: Identify customers who fine-tune your model and resell blackbox derivatives against terms.
- How: Periodically query suspected endpoints on your training examples; compute order-likelihood correlations and p-values.
- Tools/workflows: Compliance monitoring pipeline; alerting dashboards; scheduled “challenge set” probes.
- Assumptions/dependencies: Stable access to endpoints; rate limits; transcript segments for probing; acceptance of statistical thresholds.
- Evidence generation for takedowns and litigation (Policy, Legaltech)
- What: Provide quantifiable, exact statistical evidence (p-values) that a blackbox model derives from your training run.
- How: Run the permutation-based independence test framework; report Spearman/t-distribution p-values; archive test artifacts.
- Tools/workflows: “Evidence Pack” with reproducible code, test statistics, transcripts used, and random seeds.
- Assumptions/dependencies: Courts/regulators accept statistical evidence; documented, audited test pipelines; transcript disclosure scope.
- Text attribution in content moderation and trust & safety (Social media, Platforms)
- What: Attribute text (posts, comments) to a specific LM line, supporting detection of bot networks or unlabeled AI-generated content.
- How: Observational setting with reshuffle-based method (); a few hundred tokens can suffice when comparing likelihoods under the original vs. reshuffled last-phase checkpoints.
- Tools/workflows: “Text Attribution Scanner”; internal mirrors of last-phase checkpoints retrained on reshuffles; batch scoring infrastructure.
- Assumptions/dependencies: Ability to retrain last phase (1–10% of pretraining) on multiple reshuffles; access to model architecture; compute budget.
- Marketplace badge verification (“Built with X”) (Industry, Consumer trust)
- What: Verify claims that products use a licensed/open-weight base model.
- How: Run query-setting test; publish a signed verification badge tied to p-value thresholds.
- Tools/workflows: “Compliance SDK” + “Provenance Badge API”; tamper-evident audit logs.
- Assumptions/dependencies: Standardized threshold policies; data-sharing agreements for transcript subsets.
- Third-party provenance audits using shareable transcript subsets (Policy, Audit)
- What: Independent auditors validate compliance without full training data disclosure.
- How: Test against a disclosed transcript subset (e.g., ordered Wikipedia partitions); compute p-values with the same independence framework.
- Tools/workflows: “Training Transcript Registry” with hashed order commitments; auditor API.
- Assumptions/dependencies: Providers disclose minimally sufficient ordered subsets; documented shuffling; independent reference models if needed.
- Research on memorization dynamics and training-order effects (Academia)
- What: Measure and compare palimpsestic memorization across scales, datasets, and recipes.
- How: Use the query-setting correlation tests and observational reshuffle tests to quantify how training order imprints on final models.
- Tools/workflows: Open-source benchmarks, shared transcript segments, reproducible pipelines.
- Assumptions/dependencies: Access to ordered data; sufficient compute for retraining in observational tests; standardized evaluation protocols.
- Internal MLOps/IP monitoring (Industry, MLOps)
- What: Detect unauthorized downstream fine-tunes or model souping involving your base model.
- How: Query-setting tests across suspect releases; track p-values and trends; flag high-risk matches.
- Tools/workflows: Continuous provenance monitoring integrated into model release radar; anomaly detection.
- Assumptions/dependencies: Coverage of suspected models; coordination across legal/compliance; manageable query cost at scale.
Long-Term Applications
These applications require further research, standardization, scaling, or organizational adoption before widespread deployment.
- Platform-scale estimation of model-driven content share (Social media, Platforms, Policy)
- What: Measure the fraction of platform content attributable to specific model families.
- How: Observational partition/n-gram method () on large text corpora; aggregate p-values across cohorts.
- Tools/workflows: Batch attribution services; statistical aggregation dashboards; ecosystem analytics.
- Assumptions/dependencies: Many tokens per document cohort (hundreds of thousands); heavy index/storage (n-gram indices); privacy-preserving pipelines.
- Standardized provenance audit frameworks and registries (Policy, Industry)
- What: Formalize processes, thresholds, and artifacts for provenance testing (e.g., acceptable p-value ranges; transcript subsets).
- How: Multi-stakeholder working groups; NIST/ISO-like standards; shared challenge sets for blackbox testing.
- Tools/workflows: Open “Provenance Challenge” datasets; order-commitment registries; interoperable audit APIs.
- Assumptions/dependencies: Consensus on tests, metrics, and disclosure; governance around transcript handling and privacy.
- Privacy-preserving transcript sharing (Policy, Research, Security)
- What: Enable independent audits without exposing sensitive training content.
- How: Cryptographic commitments (hash chains of example order), zero-knowledge proofs, or curated public subsets with verified ordering.
- Tools/workflows: “Order Proof” protocols; secure registries; auditor tooling for verifiable random subsampling.
- Assumptions/dependencies: Robust cryptographic designs; acceptance by regulators; careful threat modeling.
- Provenance-aware licensing marketplaces (Finance, Legaltech, Software)
- What: License enforcement baked into marketplace workflows; automated pre- and post-integration checks.
- How: Integrate query-setting tests at onboarding; periodic observational checks post-deployment; pricing tied to compliance risk.
- Tools/workflows: “License Guardrails” platform; risk scoring; remediation workflows.
- Assumptions/dependencies: Commercial incentives; standardized provider disclosures; scalable compute.
- Education anti-cheating and model-attribution tools (Education, Assessment)
- What: Attribute student submissions to specific LMs where policy bans certain model use.
- How: Observational reshuffle approach; compare likelihoods under original vs. reshuffled last-phase models; thresholding for suspicion.
- Tools/workflows: Instructor portals; batch scoring on coursework; appeal/audit processes.
- Assumptions/dependencies: Provider willingness to publish order subsets or last-phase checkpoints; fairness and false-positive controls; variable token lengths of submissions.
- Training recipes to modulate palimpsestic signals (Software/AI Research, Privacy)
- What: Control how strongly training order imprints on models (strengthen for enforceability, weaken for privacy).
- How: Adjust shuffling granularity, curriculum design, regularization; paper trade-offs (quality, privacy, provenance detectability).
- Tools/workflows: “Order Sensitivity” diagnostics; training schedule optimizers.
- Assumptions/dependencies: Clear objectives; empirical characterization across scales; potential tension with model quality or regurgitation reduction.
- Differential privacy and leakage evaluation via order-correlation metrics (Privacy, Healthcare, Regulated sectors)
- What: Use palimpsestic correlation signals as indicators of memorization/leakage risk for sensitive data.
- How: Track correlation vs. order under different DP/noise regimes; incorporate into privacy audits.
- Tools/workflows: Privacy scorecards; continuous monitoring pipelines.
- Assumptions/dependencies: Access to sensitive data order (or synthetic analogs); validated link between reduced palimpsestic signals and privacy guarantees.
- Hybrid enforcement with watermarks and palimpsest-based tests (Software/AI Platforms)
- What: Combine inference-time watermarks (where feasible) with order-correlation tests (robust to fine-tunes).
- How: Layered detection pipelines: watermark checks first; fallback to statistical provenance tests.
- Tools/workflows: Multi-signal attribution services; policy engines for actions based on combined evidence.
- Assumptions/dependencies: Watermark survivability; coordination of signals; clear escalation paths.
- Procurement and regulatory standards requiring provenance testing (Policy, Public sector)
- What: Mandate provenance checks for government or regulated-sector deployments of AI systems.
- How: Include auditability clauses; require transcript subsets or order commitments; specify acceptable p-values.
- Tools/workflows: Compliance certification; audit templates; independent verification bodies.
- Assumptions/dependencies: Legislative adoption; enforcement resources; provider participation.
- Insurance and IP risk scoring based on provenance risk (Finance, Insurtech)
- What: Underwrite AI deployments with premiums linked to demonstrated provenance compliance.
- How: Integrate query/observational test results into risk models; periodic re-scoring.
- Tools/workflows: “Provenance Risk Score” API; policy management dashboards.
- Assumptions/dependencies: Market demand; legal recognition of statistical evidence; scalable testing at portfolio level.
Notes on Assumptions and Dependencies
- Ordered transcript access: All tests rely on access to the training example order (full or subset). Exact p-values assume randomized shuffling within training phases.
- Query-setting practicality: Best performance when token probabilities are available; next-token-only APIs require probability estimation via carefully designed prompts.
- Observational reshuffle method: Requires retraining multiple copies on reshuffled last-phase data; feasible at small scales (e.g., TinyStories, 1–7B checkpoints) but costly for larger models.
- Partition/n-gram method: Storage/computation-heavy (large indices); needs many tokens (hundreds of thousands) for high power; sensitive to sampling temperature/diversity.
- Robustness to evasion: Heavy post-training or large distribution shifts can reduce detection power; the paper shows evasion often degrades model quality or requires substantial finetuning.
- Reference models: When using reference likelihoods, they must be known independent of the tested transcript to preserve test validity.
- Legal/regulatory context: Adoption depends on acceptance of statistical evidence and standardized thresholds for action.
Glossary
- backdoor trigger: A deliberately embedded pattern that causes a model to produce a specific response, used for fingerprinting or identifying derivatives. Example: "by planting a backdoor trigger"
- blackbox: Refers to a model or system that can be queried for inputs/outputs but whose internals (e.g., weights, architecture) are not accessible. Example: "blackbox derivative of Alice's model"
- canary: An artificial secret inserted into training to test memorization or provenance (e.g., random strings). Example: "inserting canaries into Alice's model"
- checkpoint: A saved snapshot of model parameters at a particular point during training. Example: "from an intermediate checkpoint"
- cooldown phase: A late stage of pretraining with possibly adjusted learning dynamics, used in OLMo training. Example: "from the cooldown phase of their pretraining run"
- dataset inference: A technique for testing whether a model trained on a dataset by comparing performance on training vs. held-out data. Example: "they term dataset inference"
- deduped: A dataset variant where duplicate content has been removed to reduce memorization and redundancy. Example: "the deduped version of The Pile"
- derivative model: A model produced by further training, adapting, or otherwise transforming a base model. Example: "downstream identification of derivative models."
- exact p-values: P-values computed without approximation (e.g., via permutation), providing precise Type I error control. Example: "obtaining exact p-values from arbitrary test statistics"
- fine-tuning: Post-training adaptation of a pre-trained model on additional data or objectives. Example: "fine-tuned from a Pythia checkpoint"
- held-out test set: A dataset not used in training, reserved for evaluation. Example: "a small i.i.d. held-out test set"
- i.i.d.: Independent and identically distributed; a standard assumption about samples in statistical testing. Example: "a small i.i.d. held-out test set"
- independence testing: Statistical testing to determine if two random variables (e.g., a model and a training transcript) are independent. Example: "We formulate this question as an independence testing problem"
- inference-time watermarks: Techniques that embed detectable signals into generated text during inference for later attribution. Example: "inference-time watermarks"
- log-likelihood: The logarithm of the probability a model assigns to observed data; used to quantify fit and memorization. Example: "We regress the negative log-likelihoods of pythia-6.9b-deduped"
- membership inference: Inferring whether a data point (or its order) was part of a model’s training process. Example: "via Palimpsestic Membership Inference"
- model fingerprinting: Methods that implant identifiable patterns or behaviors in a model to verify lineage or ownership. Example: "under the umbrella of model fingerprinting has developed a multitude of ways"
- model provenance: The origin and lineage of a model, including data and training process. Example: "Model provenance."
- model souping: Combining multiple fine-tuned model checkpoints—often by weight averaging—to form a new model. Example: "model souping (i.e., averaging multiple finetuned model weights)"
- null hypothesis: The default assumption that two variables (e.g., Bob’s model and Alice’s transcript) are independent. Example: "the null hypothesis is that Bob's model or text is independent of Alice's randomized training run"
- n-gram: A contiguous sequence of n tokens, used to paper overlap and memorization in text. Example: "n-gram overlap"
- observational setting: The scenario where only generated text is observed, without direct access to the model. Example: "In the observational setting, we try two approaches"
- open-weight LLM: A model whose weights are publicly available for use and analysis. Example: "Suppose Alice trains an open-weight LLM"
- p-value: The probability, under the null hypothesis, of observing a test statistic at least as extreme as the one obtained. Example: "achieving a p-value on the order of at most "
- palimpsest: A medium written over after erasing prior text; metaphor for later training overwriting earlier influences. Example: "A palimpsest is a ``writing material (such as a parchment or tablet) used one or more times after earlier writing has been erased''"
- palimpsestic memorization: The tendency of models to memorize later-seen training data more strongly, overwriting earlier effects. Example: "LLMs exhibit palimpsestic memorization"
- preference optimization: Post-training methods that optimize models to align with preferences (e.g., RLHF variants). Example: "including supervised finetuning, preference optimization, and model souping"
- pretraining: The initial large-scale training phase on broad data before task-specific adaptation. Example: "pretraining run"
- query setting: The scenario where the model can be directly queried to obtain probabilities or outputs. Example: "In the query setting, we directly estimate (via prompting) the likelihood"
- reference model: An auxiliary, independent model used to normalize or control variability in likelihoods. Example: "an independent reference model "
- regurgitate: When a model reproduces memorized text from its training data verbatim or near-verbatim. Example: "tend to regurgitate memorized phrases (from training data)"
- shuffled data: Training data whose order is randomized to enable statistical independence assumptions. Example: "randomly shuffled data"
- Spearman rank correlation coefficient: A nonparametric measure of rank correlation used to relate likelihoods to training order. Example: "with denoting the Spearman rank correlation coefficient"
- statistical power: The probability that a test correctly rejects a false null hypothesis. Example: "the test should have high power"
- t-distribution: The sampling distribution of a standardized statistic under the null, used for p-values with small samples. Example: "follows a t-distribution with degrees of freedom."
- text provenance: The origin and attribution of a piece of text, including whether it was model-generated. Example: "Text provenance."
- z-score: A standardized score measuring how many standard deviations an observation is from the mean, used for approximate p-values. Example: "by treating the output of as a z-score"
Collections
Sign up for free to add this paper to one or more collections.