MetaCluster: Enabling Deep Compression of Kolmogorov-Arnold Network (2510.19105v1)
Abstract: Kolmogorov-Arnold Networks (KANs) replace scalar weights with per-edge vectors of basis coefficients, thereby boosting expressivity and accuracy but at the same time resulting in a multiplicative increase in parameters and memory. We propose MetaCluster, a framework that makes KANs highly compressible without sacrificing accuracy. Specifically, a lightweight meta-learner, trained jointly with the KAN, is used to map low-dimensional embedding to coefficient vectors, shaping them to lie on a low-dimensional manifold that is amenable to clustering. We then run K-means in coefficient space and replace per-edge vectors with shared centroids. Afterwards, the meta-learner can be discarded, and a brief fine-tuning of the centroid codebook recovers any residual accuracy loss. The resulting model stores only a small codebook and per-edge indices, exploiting the vector nature of KAN parameters to amortize storage across multiple coefficients. On MNIST, CIFAR-10, and CIFAR-100, across standard KANs and ConvKANs using multiple basis functions, MetaCluster achieves a reduction of up to 80$\times$ in parameter storage, with no loss in accuracy. Code will be released upon publication.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
What this paper is about
This paper shows a new way to make a special kind of neural network, called a Kolmogorov–Arnold Network (KAN), much smaller without losing accuracy. The method is called MetaCluster. It shrinks the memory needed to store the network by up to 80 times while keeping the same performance on image tasks like MNIST, CIFAR-10, and CIFAR-100.
The main questions the paper asks
- KANs can be very accurate, but they use a lot of memory. Can we make them much smaller without hurting accuracy?
- Why is it hard to compress KANs the usual way, and how can we fix that?
- Can a small “helper” network shape KAN’s parameters so they become easier to compress?
Quick background: What is a KAN?
In a regular neural network, each connection between two neurons has one number (a weight). In a KAN, each connection is more powerful: it has several numbers (a vector of coefficients) that build a tiny “custom function” using building blocks called basis functions (like B-splines or radial basis functions). This makes KANs flexible and accurate—but also much bigger. If each connection stores, say, 10 numbers instead of 1, the whole model can be about 10 times larger.
Why usual compression struggles with KANs
A common way to compress networks is “weight sharing,” which means:
- Group similar weights together into a small set of shared values (a “codebook”), and
- For each original weight, store only a small index pointing to which shared value to use.
This works well for regular networks with single numbers per connection. But in KANs, each connection is a vector. Grouping high‑dimensional vectors is hard because, in many dimensions, points start to look equally far apart. It’s like trying to sort socks in a room with the lights off—everything blends together, so grouping goes wrong.
How MetaCluster works
MetaCluster fixes that by reshaping the space before grouping. Think of it as tidying a messy room before you sort your socks.
Step 1: Teach a small “helper” to shape the weights
- Add a tiny network (a meta-learner) that takes a short code (a low-dimensional embedding) and produces the full vector of KAN coefficients for each connection.
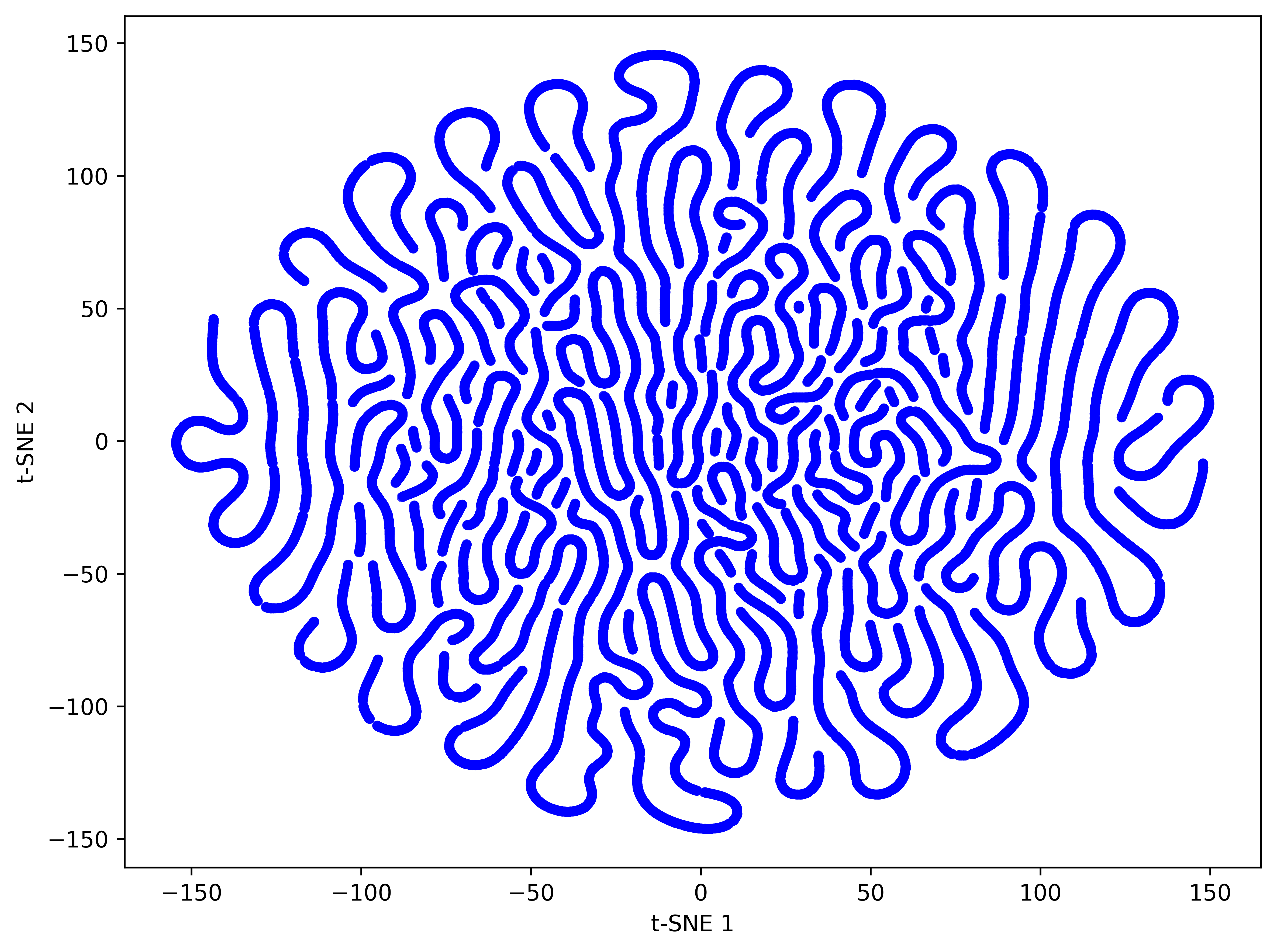
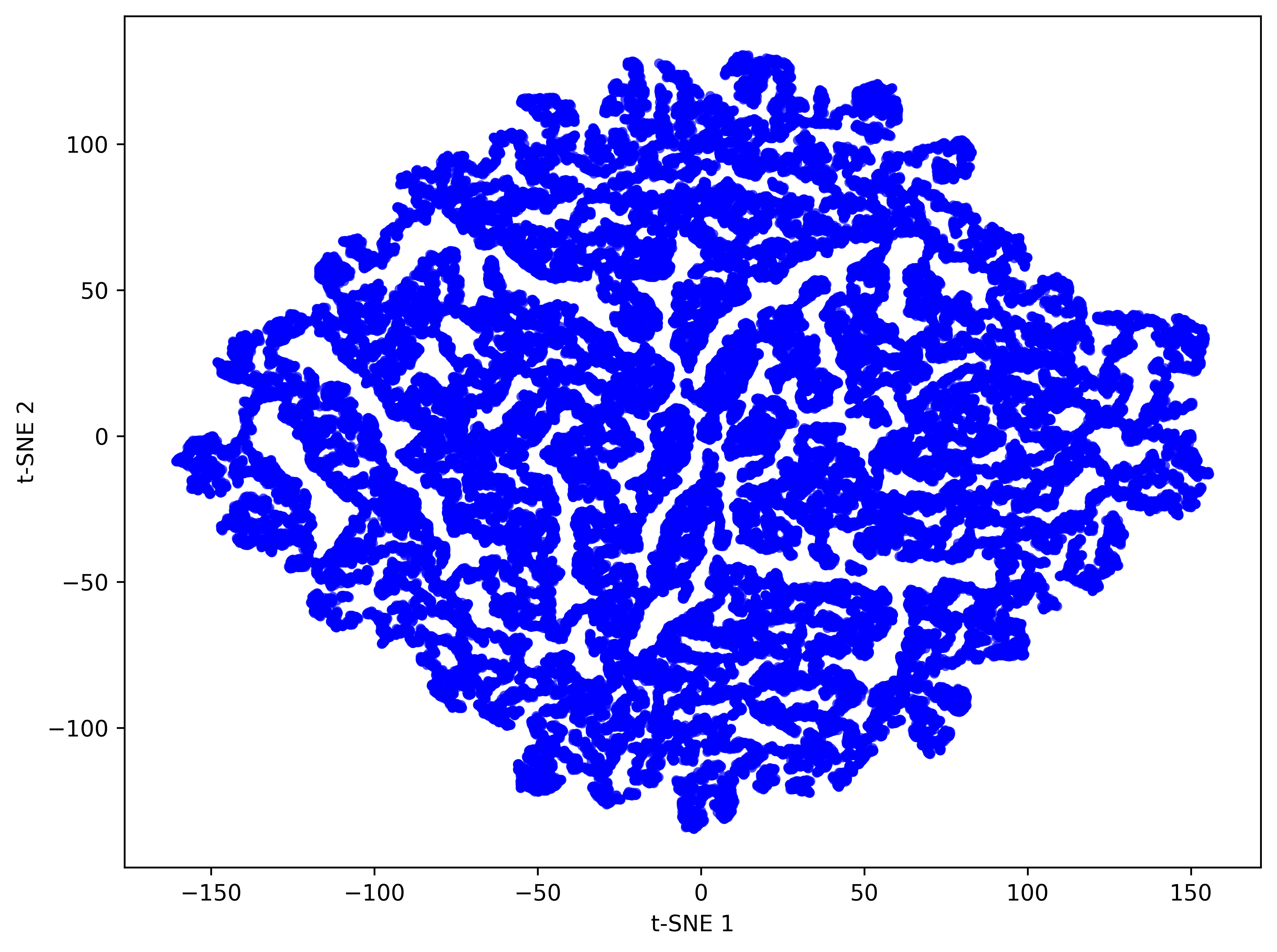
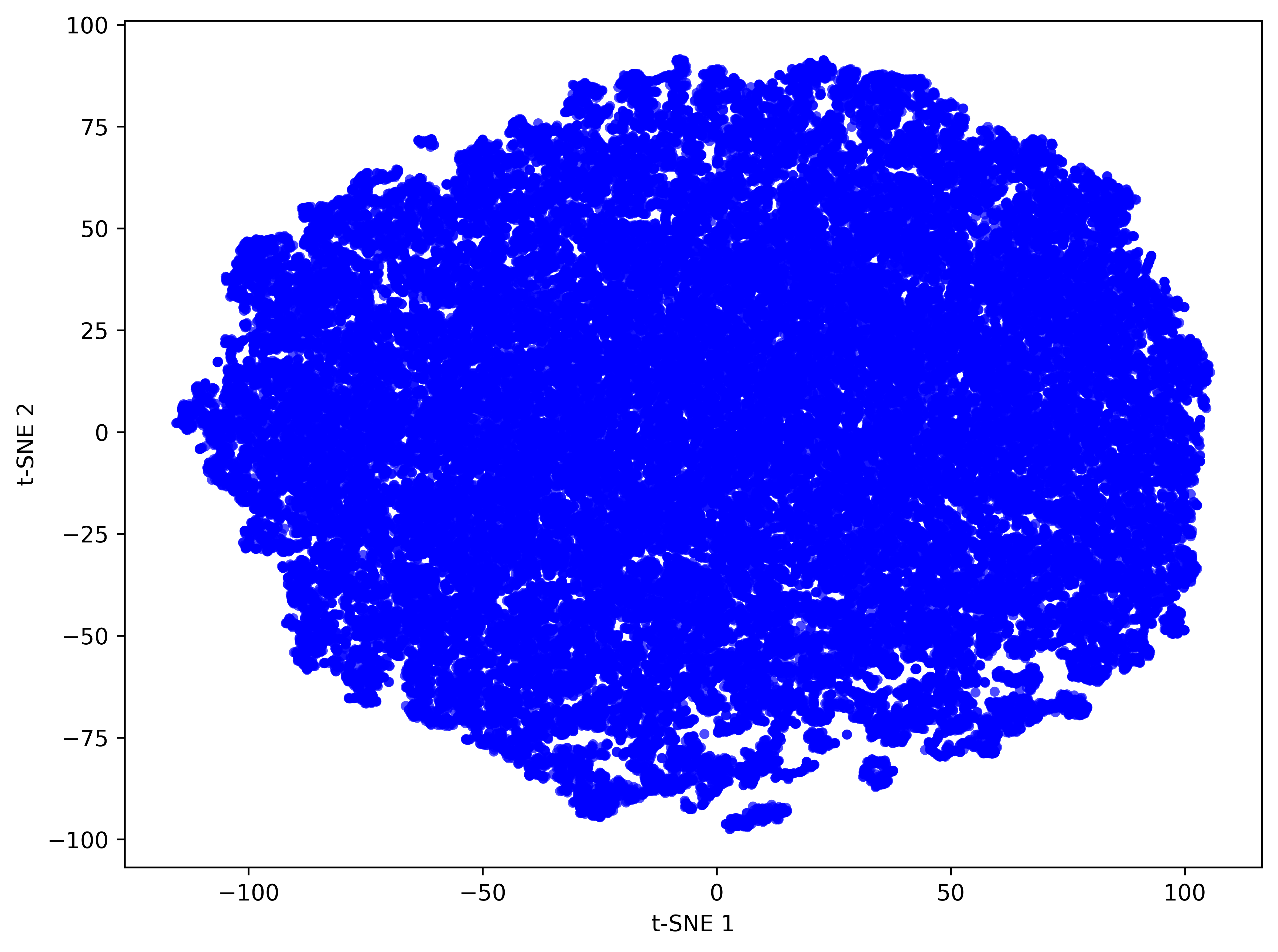
- During training, this helper learns to generate coefficient vectors that lie on a simple, low-dimensional “shape” (a manifold). In plain terms: all those vectors start to follow a clear pattern instead of being scattered randomly.
- Result: similar connections end up close together, which makes grouping them much easier.
Step 2: Group similar vectors with K-means
- Use K-means (a standard “group similar things” algorithm) to cluster the coefficient vectors into k groups.
- For each group, store only the average vector (a centroid) in a small codebook.
- For every connection, keep just a tiny index that says “use centroid #7,” “use centroid #3,” etc.
Analogy: You don’t keep every unique shade of blue sock. You keep a small set of standard blues and label each sock with which blue it matches best.
Step 3: Remove the helper and touch up
- After clustering, throw away the meta-learner and its embeddings—you don’t need them anymore.
- Briefly fine-tune only the codebook (the centroids) to recover any small drop in accuracy.
- Now the model stores just a small codebook plus small indices per connection.
Why this is extra good for KANs: each centroid stores a whole vector (many numbers) at once. So the cost of the small indices gets “spread out” over many numbers, making compression especially effective.
What they tested
The authors tried MetaCluster on:
- Datasets: MNIST, CIFAR-10, and CIFAR-100.
- Models: fully connected KANs and convolutional KANs (ConvKANs).
- Different basis functions: B-splines, radial basis functions (RBFs), and Gram polynomials.
They also ran studies to see:
- How the number of clusters affects accuracy.
- How the size of the coefficient vectors and the meta-learner’s embedding size matter.
Main findings and why they’re important
- Huge memory savings with no accuracy loss: Up to 80× reduction in storage compared to the original KANs, while matching accuracy on multiple datasets and architectures.
- Works across many settings: Effective for fully connected and convolutional KANs and for different basis functions (B-splines, RBFs, Gram).
- Clustering alone isn’t enough: If you try to cluster KAN weights directly (without the meta-learner), accuracy often drops a lot. The meta-learner’s “manifold shaping” is the key that makes clustering work well.
- Little extra training needed: After clustering, a short fine-tuning step of the small codebook recovers any small accuracy loss.
- No extra cost at runtime: The meta-learner is only used during training. It’s removed afterward, so inference stays fast and simple.
Why this matters: KANs are powerful but memory-hungry. MetaCluster turns them into compact models you could deploy on memory-limited devices (like phones or tiny edge hardware) without sacrificing accuracy.
What this could lead to
- Easier deployment: Smaller KANs can run on devices with limited memory and storage.
- Larger models within the same budget: You can fit stronger KANs into the same memory limit by compressing them with MetaCluster.
- Combine with other tricks: This method can likely be paired with quantization (using fewer bits per number) for even more compression.
- General idea: “Shape first, cluster second” could help compress other models that have vector-based parameters, not just KANs.
Key takeaways
- KANs are big because each connection stores a vector of coefficients, not just one number.
- Clustering those vectors directly doesn’t work well in high dimensions.
- MetaCluster uses a small helper network to shape those vectors into a simple pattern, making them easy to cluster.
- After clustering, the model keeps only a tiny codebook and indices, drops the helper, and lightly fine-tunes.
- Result: up to 80× smaller models with no accuracy loss across several datasets and KAN types.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a single, concise list of specific gaps and open questions that remain unresolved by the paper and could guide future research.
- Method scope: validated only on small/medium-scale image classification (MNIST, CIFAR-10/100) with shallow FC and modest ConvKANs; no results on large-scale datasets (e.g., ImageNet), larger/deeper KANs, or transformer-style KANs (e.g., KAT).
- Task generality: no evaluation on scientific ML/equation modeling or regression tasks where KANs are most popular; unclear if manifold shaping and clustering preserves accuracy for PDEs, dynamics, or inverse problems.
- Runtime behavior: inference-time latency and throughput impacts of centroid lookups and irregular memory access are not measured; no kernel-level or hardware-level performance/energy profiling provided.
- Storage realism: memory accounting assumes idealized index and codebook storage; no analysis of alignment/padding, dtype choices (fp32/fp16/bf16), or real-world file/GPU-memory overheads for indices and codebooks.
- Training cost: extra training-time overhead (meta-learner optimization, clustering passes, centroid fine-tuning) is unquantified (wall-clock time, FLOPs, memory, GPU hours).
- Statistical robustness: results are presented without multiple seeds/variances or significance tests; sensitivity to random initialization and K-means seeding is unknown.
- Hyperparameter selection: no principled procedure to choose embedding dimension, hidden size of meta-learner, number of clusters per layer, or fine-tuning duration; automated selection criteria or heuristics are absent.
- Layerwise strategy: uniform cluster counts (e.g., k=16) are used; no paper of per-layer codebooks, heterogeneous k across layers, or shared vs layer-specific codebooks.
- Assignment optimization: indices are fixed after K-means; no exploration of joint centroid–assignment optimization (e.g., DKM), assignment refinement during fine-tuning, or alternating re-clustering schedules.
- Clustering alternatives: only vanilla Euclidean K-means is evaluated; no comparison to Hessian-weighted K-means, product/vector quantization (PQ/VQ), GMM/soft weight sharing, subspace clustering, or learned quantization layers.
- Distance normalization: coefficient vectors may have scale or basis-specific anisotropy; no investigation of preconditioning/whitening, basis-aware metrics, or layer-wise normalization before clustering.
- Theoretical guarantees: no formal analysis linking intrinsic dimension, clustering error, and generalization; no bounds relating embedding dimension and achievable compression–accuracy trade-offs.
- Manifold evidence: manifold claim is supported via t-SNE visualizations only; no quantitative measures (e.g., PCA explained variance, participation ratio, manifold dimension estimators, silhouette scores) pre/post meta-learner.
- Basis generality: tested on B-splines, RBFs, and Gram polynomials; not evaluated on other proposed KAN bases (Chebyshev, Legendre, wavelets, rational) or mixed-basis settings; cross-basis transferability is unknown.
- Extreme coefficient regimes: amortization benefits depend on coefficient length |w|; behavior for very small (e.g., |w|≤3) or very large coefficient vectors is not characterized.
- Compression stacking: quantization is stated as “orthogonal” but not tested; no experiments combining MetaCluster with pruning, low-rank factorization, or entropy coding (e.g., Huffman, ANS) to assess compound gains.
- Fine-tuning protocol: centroid-only fine-tuning is brief (β epochs) and fixed; sensitivity to longer schedules, learning-rate/batch-size choices, and whether training assignments or embeddings should also be adapted is not explored.
- Post-hoc compressibility: the method assumes training with a meta-learner; no pathway to compress an existing trained KAN without re-training (e.g., distilling a meta-learner to fit fixed weights, or manifold-regularized post-hoc clustering).
- Failure modes: cases where meta-manifold constraints harm expressivity (e.g., highly heterogeneous per-edge functions) are not analyzed; no diagnostics to detect over-constraining or to adaptively increase embedding dimension.
- Robustness: no tests under distribution shift, corruptions (e.g., CIFAR-C), or adversarial perturbations; unknown if shared centroids amplify or mitigate robustness issues.
- Scalability of clustering: time/memory complexity of clustering millions of high-dimensional per-edge vectors (especially in large ConvKANs) is not reported; no discussion of mini-batch or approximate K-means variants.
- Codebook granularity: unclear whether centroids are global, per-layer, or per-channel for conv layers; no comparison across these granularities.
- Hardware mapping: no discussion of index tensor layouts, cache locality, vectorization of centroid gathers, or custom kernels to accelerate centroid lookups on GPUs/NPUs.
- Precision sensitivity: codebook precision (fp32 vs fp16/bf16/int) and its impact on accuracy/compression is not studied; no guidance on safe dtypes for centroids/indices.
- Regularization design: beyond using a meta-learner, no explicit regularizers to encourage clusterability (e.g., k-means loss, group-lasso, mutual information bottlenecks) are evaluated.
- Reproducibility: code is not yet released; some crucial hyperparameters (e.g., α, β, embedding dimension per experiment) are deferred to appendices and not fully specified in the main text.
Practical Applications
Immediate Applications
The following applications can be deployed now, leveraging MetaCluster’s demonstrated ability to compress Kolmogorov–Arnold Networks (KANs) by up to 80× with no accuracy loss on MNIST, CIFAR-10, and CIFAR-100, across multiple KAN variants (B-splines, RBFs, Gram polynomials) and both fully connected and convolutional architectures.
- Edge deployment of KAN-based vision models on mobile and embedded devices
- Sector: software, robotics, consumer electronics
- What: Deploy ConvKAN/MetaClusterKANConv models for on-device image classification, object detection, and scene understanding where memory is constrained (AR headsets, drones, smart cameras).
- Tools/workflows: A PyTorch/TensorFlow “KAN Compressor” plugin that adds a meta-learner during training, runs K-means on coefficient vectors, replaces per-edge vectors with codebook indices, then fine-tunes centroids; export to ONNX with codebook + indices.
- Assumptions/dependencies: KAN-based models in use; access to training pipeline to run meta-learning + clustering; modest fine-tuning budget; codebook lookup supported by the runtime.
- Lower VRAM footprint for KAN inference in the cloud
- Sector: software, cloud infrastructure
- What: Serve compressed KANs for computer vision or scientific ML services to reduce instance sizes, lower memory bandwidth, and increase model density per GPU/CPU.
- Tools/workflows: Model conversion stage in MLOps that outputs codebook + per-edge indices and replaces dense coefficient tensors; inference framework that caches the codebook and resolves indices at load.
- Assumptions/dependencies: Existing KAN services; small runtime overhead from index indirection is acceptable; accurate centroids after fine-tuning.
- On-device privacy-preserving analytics using KANs
- Sector: healthcare, finance, consumer apps
- What: Run KAN-based classification/segmentation locally to avoid data upload (e.g., medical image pre-screening, financial anomaly detection on personal devices).
- Tools/workflows: MetaCluster-trained models packaged as lightweight mobile libraries; optional post-training quantization of the codebook for further memory cuts.
- Assumptions/dependencies: KANs match task accuracy; regulatory/security requirements met; device supports local inference with codebook-based parameters.
- Scientific and industrial time-series modeling with compressed KANs
- Sector: energy, manufacturing, IoT
- What: Use compact KANs for KAN-ODEs and dynamical systems learning (e.g., predictive maintenance, grid anomaly detection) on microcontrollers and gateways.
- Tools/workflows: Training with MetaCluster; deployment via microcontroller-friendly runtimes (e.g., TVM/ONNX Runtime); codebook stored in SRAM, indices in flash.
- Assumptions/dependencies: Continuous signals mapped to KAN architectures; device toolchains support codebook lookup; K-means initialization stable.
- Academic reproducibility and teaching kits for KAN compression
- Sector: academia, education
- What: Provide course labs and notebooks where students train KANs, apply MetaCluster, and observe accuracy-memory trade-offs and manifold shaping effects.
- Tools/workflows: Ready-to-run notebooks with visualization (t-SNE of coefficient vectors), automated clustering and fine-tuning; small datasets (MNIST/CIFAR) for quick demos.
- Assumptions/dependencies: Availability of open-source code; KAN frameworks installed; basic GPU/CPU resources for training/fine-tuning.
- MLOps integration for KAN compression and export
- Sector: software/ML infrastructure
- What: Add a “KAN compression” stage in CI/CD pipelines that outputs a codebook-centric model artifact; optionally stack quantization/Huffman coding on top.
- Tools/workflows: CLI/SDK that integrates MetaCluster; artifact format with codebook tensors + index maps; validation step to confirm accuracy parity after fine-tuning.
- Assumptions/dependencies: Organizational adoption of KANs; build systems that can re-train/fine-tune models; monitoring to detect accuracy drift.
- Energy and cost savings reporting for compressed KAN deployments
- Sector: policy, sustainability, IT governance
- What: Track and report energy reductions from lower memory footprints in inference clusters and edge fleets; include “Green AI” metrics in procurement documents.
- Tools/workflows: Estimation tools (e.g., adapted Deep k-Means energy metrics) tied to memory I/O reduction; dashboards summarizing compression gains and accuracy.
- Assumptions/dependencies: Acceptance of proxy metrics for energy (memory bandwidth/I/O); alignment with internal sustainability goals.
Long-Term Applications
These applications require further research, scaling, ecosystem development, or hardware/software co-design to realize their full potential.
- Foundation-scale KANs for vision and multimodal models (e.g., Kolmogorov–Arnold Transformer)
- Sector: software, AI research
- What: Use MetaCluster to make large KAN-based transformers (KAT) practical by aggressively compressing coefficient vectors without accuracy loss; enable broader KAN adoption at scale.
- Tools/workflows: End-to-end training recipes that embed meta-learner + clustering into transformer training; auto-tuning of embedding size and cluster count for each layer.
- Assumptions/dependencies: Demonstrated parity of KANs with mainstream architectures at scale; stability of clustering/fine-tuning in very large models; robust multi-GPU training support.
- Hardware co-design for codebook-centric inference
- Sector: semiconductors, edge hardware
- What: Design accelerators that natively support index-based weight sharing (codebook caches, fast centroid lookup, compressed on-chip storage), reducing latency and energy.
- Tools/workflows: ISA/runtime extensions for codebook addressing; compiler passes that schedule centroid reuse; SRAM partitioning optimized for centroid access patterns.
- Assumptions/dependencies: Hardware vendor support; clear performance benefits over dense weights; standardization of compressed model formats.
- Standardized compressed KAN formats and ONNX/TVM support
- Sector: software, standards
- What: Extend model interchange formats (ONNX) with native constructs for codebooks and per-edge indices; enable general inference engines to consume MetaCluster artifacts.
- Tools/workflows: Spec proposals; reference implementations in ONNX Runtime/TVM; validators for accuracy and compatibility.
- Assumptions/dependencies: Community consensus; backwards compatibility; support across major frameworks.
- Automated compression policies combining MetaCluster with quantization, pruning, and Huffman coding
- Sector: software tooling, AutoML
- What: Build AutoML systems that optimize embedding dimension, cluster count, bit-width, and pruning thresholds jointly for KANs under accuracy/latency/memory constraints.
- Tools/workflows: Multi-objective optimization pipelines; differentiable K-means variants; hyperparameter search guided by storage analysis (e.g., ).
- Assumptions/dependencies: Reliable surrogates for accuracy/energy; training budgets for iterative search; heterogeneous deployment targets.
- Compressed KANs in clinical workflows and portable medical imaging
- Sector: healthcare
- What: Integrate MetaCluster-compressed U-KAN backbones in point-of-care devices (portable ultrasound, dermoscopy) to deliver real-time segmentation/generation without cloud reliance.
- Tools/workflows: FDA/CE-compliant pipelines; field updates with codebook-only patches; on-device fine-tuning for site-specific data if regulations permit.
- Assumptions/dependencies: Clinical validation in target modalities; safety and reliability guarantees; integration with hospital PACS/EMR systems.
- Privacy-first finance analytics with compact KANs
- Sector: finance
- What: Use compressed KANs for on-device or branch-level time-series modeling (risk scoring, fraud detection) to minimize sensitive data movement.
- Tools/workflows: Federated learning setups where only codebooks are updated; audit trails for compression-induced changes; explainability modules for KAN decisions.
- Assumptions/dependencies: Evidence of KAN superiority in financial time series; regulatory acceptance; robust edge deployment in mixed hardware environments.
- Large-scale sensor networks and digital twins powered by KAN-ODEs
- Sector: energy, smart cities, industrial IoT
- What: Roll out compressed KAN models in distributed sensor networks to learn dynamics, run inference on low-power nodes, and synchronize with digital twins.
- Tools/workflows: Hierarchical compression strategies (global codebook + local indices); streaming fine-tuning of centroids; twin synchronization APIs.
- Assumptions/dependencies: Proven accuracy on complex dynamics; resilient decentralized training/inference; operational tooling for versioning compressed models.
- Procurement and certification frameworks for compressed AI
- Sector: policy, governance
- What: Establish guidelines that prefer memory- and energy-efficient models (like MetaCluster-compressed KANs) in public-sector RFPs; certify “efficient by design” AI.
- Tools/workflows: Benchmarks and thresholds for compression ratio, energy per inference, and accuracy deviation; third-party audits and badges.
- Assumptions/dependencies: Policy-maker engagement; transparent reporting; sector-specific performance baselines.
- Developer ecosystems and libraries centered on coefficient-vector architectures
- Sector: software, education
- What: Build community libraries for KAN variants (RBF, Gram, Chebyshev, wavelet, rational) with built-in MetaCluster compression, visualization, and diagnostics.
- Tools/workflows: Unified APIs for basis selection; manifold visualizers; error analysis tools linking centroid assignments to task loss.
- Assumptions/dependencies: Continued growth of KAN research; maintainers for multi-basis support; stable API across platforms.
Notes on feasibility across applications:
- The method depends on KAN architectures having per-edge coefficient vectors; benefits grow with coefficient dimensionality ().
- Successful compression relies on effective manifold shaping via a meta-learner; clustering quality (K-means initialization and cluster count) and brief fine-tuning are key to accuracy recovery.
- Runtime involves codebook + index indirection rather than a hypernetwork; minimal overhead if inference engines handle indexed lookups efficiently.
- Combining MetaCluster with post-training quantization is complementary and can further reduce memory; care should be taken to preserve accuracy.
Glossary
- AdamW: An optimization algorithm that decouples weight decay from the gradient-based update in Adam. "We train with AdamW \citep{loshchilov2017decoupled} and for at most 50 epochs, with early stopping (patience = 10)."
- Ablation study: A controlled analysis that isolates and evaluates the contribution of specific components of a method. "we conduct extensive experiments and an ablation study on both fully-connected and convolutional architectures."
- Basis coefficients: The learnable parameters that weight basis functions to form an activation function on each edge. "replace scalar weights with per-edge vectors of basis coefficients"
- Basis functions: A set of predefined functions whose weighted sum approximates an activation or target function. "has been through a weighted summation of basis functions"
- B-spline: A family of piecewise polynomial basis functions used for flexible function approximation. "each connection carries a vector of basis coefficients (e.g., B-spline weights)"
- Centroid codebook: A compact dictionary of cluster centroids used for weight sharing and indexing. "a brief fineâtuning of the centroid codebook recovers any residual accuracy loss."
- Centroids: The mean vectors representing clusters in K-means, used to replace original parameters. "The centroids are updated iteratively according to the standard K-means update rule:"
- Codebook: The set of shared parameter values (e.g., centroids) alongside indices mapping original parameters to shared entries. "stores only a small codebook and per-edge indices"
- ConvKAN: A convolutional Kolmogorov–Arnold Network variant applying KAN activations within convolutional layers. "a convolutional KAN (ConvKAN) \citep{bodner2024convolutional, drokin2024kolmogorov}."
- Curse of dimensionality: The phenomenon where high-dimensional spaces make distances concentrate and clustering harder. "With such an effect brought by the curse of dimensionality, typical clustering methods struggle to form tight clusters"
- Embedding: A lower-dimensional representation that the meta-learner maps to full coefficient vectors. "is used to map lowâdimensional embedding to coefficient vectors"
- Fine-tuning: Brief additional training after compression to recover performance losses. "lightly fineâtune the centroids to recover any accuracy loss."
- Gram polynomials: Orthogonal polynomials used as basis functions for KAN activations. "and Gram polynomials as the bases"
- HyperNetworks: Networks that generate parameters of another network, reducing direct parameter storage. "Hypernetworks reduce trainable parameter counts by replacing task or instance-specific weights with a shared generator that predicts them on demand."
- Index mapping vector: A vector of cluster assignments indicating which centroid each parameter maps to. "we define an index mapping vector "
- K-means: A clustering algorithm that partitions data into k clusters by minimizing squared distances to centroids. "We then run K-means in coefficient space and replace perâedge vectors with shared centroids."
- Kolmogorov–Arnold Networks (KANs): Neural networks where each edge applies a learned univariate function parameterized by basis coefficients. "Kolmogorov-Arnold Networks (KANs) replace scalar weights with per-edge vectors of basis coefficients"
- Kolmogorov–Arnold representation theorem: A theorem stating any continuous multivariate function on a bounded domain can be decomposed into sums of compositions of univariate functions. "Their design is motivated by the KolmogorovâArnold representation theorem"
- Manifold: A low-dimensional structure in which high-dimensional data (e.g., coefficient vectors) are constrained to lie. "shaping them to lie on a lowâdimensional manifold that is amenable to clustering."
- Meta-learner: A small auxiliary network that maps embeddings to per-edge coefficient vectors during training. "a lightweight metaâlearner, trained jointly with the KAN, is used to map lowâdimensional embedding to coefficient vectors"
- Meta-learning: A strategy where a model learns to generate or adapt parameters, often via a hypernetwork or meta-learner. "We propose a meta-learning approach that shapes per-edge KAN coefficients to lie on a low-dimensional manifold"
- MetaCluster: The proposed framework combining meta-learned manifold shaping with K-means weight sharing to compress KANs. "We propose MetaCluster, a framework that makes KANs highly compressible without sacrificing accuracy."
- Radial basis functions (RBFs): Localized basis functions used for interpolation and approximation, often Gaussian-shaped. "we test the efficacy of using B-Splines, radial basis functions (RBFs), and Gram polynomials as the bases"
- SiLU activation: The Sigmoid-Weighted Linear Unit activation function. "Each KAN variant uses a SiLU activation \citep{elfwing2018sigmoid}."
- t‑SNE: A dimensionality-reduction technique for visualizing high-dimensional data in 2D/3D. "visualize them with tâSNE."
- Weight sharing: A compression technique that clusters parameters and stores shared centroids plus compact indices. "Weight sharing is one method that reduces dimensionality directly by clustering parameters into a small codebook and storing compact indices."
- Within‑cluster sum of squares: The objective minimized by K-means measuring total squared distance of points to their assigned centroids. "assignments that minimize withinâcluster sum of squares"
Collections
Sign up for free to add this paper to one or more collections.