Generalization Below the Edge of Stability: The Role of Data Geometry (2510.18120v1)

Abstract: Understanding generalization in overparameterized neural networks hinges on the interplay between the data geometry, neural architecture, and training dynamics. In this paper, we theoretically explore how data geometry controls this implicit bias. This paper presents theoretical results for overparameterized two-layer ReLU networks trained below the edge of stability. First, for data distributions supported on a mixture of low-dimensional balls, we derive generalization bounds that provably adapt to the intrinsic dimension. Second, for a family of isotropic distributions that vary in how strongly probability mass concentrates toward the unit sphere, we derive a spectrum of bounds showing that rates deteriorate as the mass concentrates toward the sphere. These results instantiate a unifying principle: When the data is harder to "shatter" with respect to the activation thresholds of the ReLU neurons, gradient descent tends to learn representations that capture shared patterns and thus finds solutions that generalize well. On the other hand, for data that is easily shattered (e.g., data supported on the sphere) gradient descent favors memorization. Our theoretical results consolidate disparate empirical findings that have appeared in the literature.

• The paper establishes that data shatterability directly influences the implicit regularization of gradient descent in BEoS regimes.
• It derives dimension-adaptive generalization bounds for two-layer ReLU networks, linking intrinsic data geometry to training dynamics.
• Empirical validations confirm that data geometry affects neuron activation and overfitting behavior across synthetic and real datasets.

Generalization Below the Edge of Stability: The Role of Data Geometry

Introduction and Theoretical Framework

This paper rigorously investigates the interplay between data geometry, neural architecture, and training dynamics in overparameterized two-layer ReLU networks trained below the Edge of Stability (EoS). The central thesis is that data shatterability—the ease with which data can be partitioned by ReLU activation thresholds—governs the strength of implicit regularization induced by gradient descent (GD) in the EoS regime. The authors formalize this principle and derive generalization bounds that adapt to the intrinsic dimension of the data and its radial concentration, providing a unified explanation for disparate empirical phenomena in deep learning.

The analysis is situated in the feature-learning regime, focusing on dynamically stable solutions reachable by GD, characterized by the Below-Edge-of-Stability (BEoS) condition: $\lambda_{\max}(\nabla^2 L(\theta)) \leq 2/\eta$ for learning rate $\eta$. The paper leverages the connection between BEoS and a data-dependent weighted path norm, where the weight function $g$ is determined by the empirical data distribution. This framework enables width-agnostic generalization guarantees and highlights the critical role of data geometry in shaping the effective hypothesis class.

Data Shatterability: Geometric Intuition and Formalization

The concept of data shatterability is illustrated through two canonical scenarios:

1. Low-Dimensional Subspace Mixtures: When data is supported on a union of $m$-dimensional subspaces in $\mathbb{R}^d$ ($m < d$), the decision boundaries of ReLU neurons reduce to a finite set of knots along each subspace. The complexity of the network is thus governed by the locations and magnitudes of these knots, and the implicit regularization adapts to the intrinsic dimension $m$ rather than the ambient dimension $d$.
2. Isotropic Distributions with Radial Concentration: For data distributions parameterized by a concentration parameter $\alpha$, as mass concentrates toward the boundary of the unit ball (i.e., the sphere), the data becomes more shatterable. The network can partition the sphere into a large number of non-overlapping caps, each containing equal probability mass, enabling memorization via highly specialized neurons.

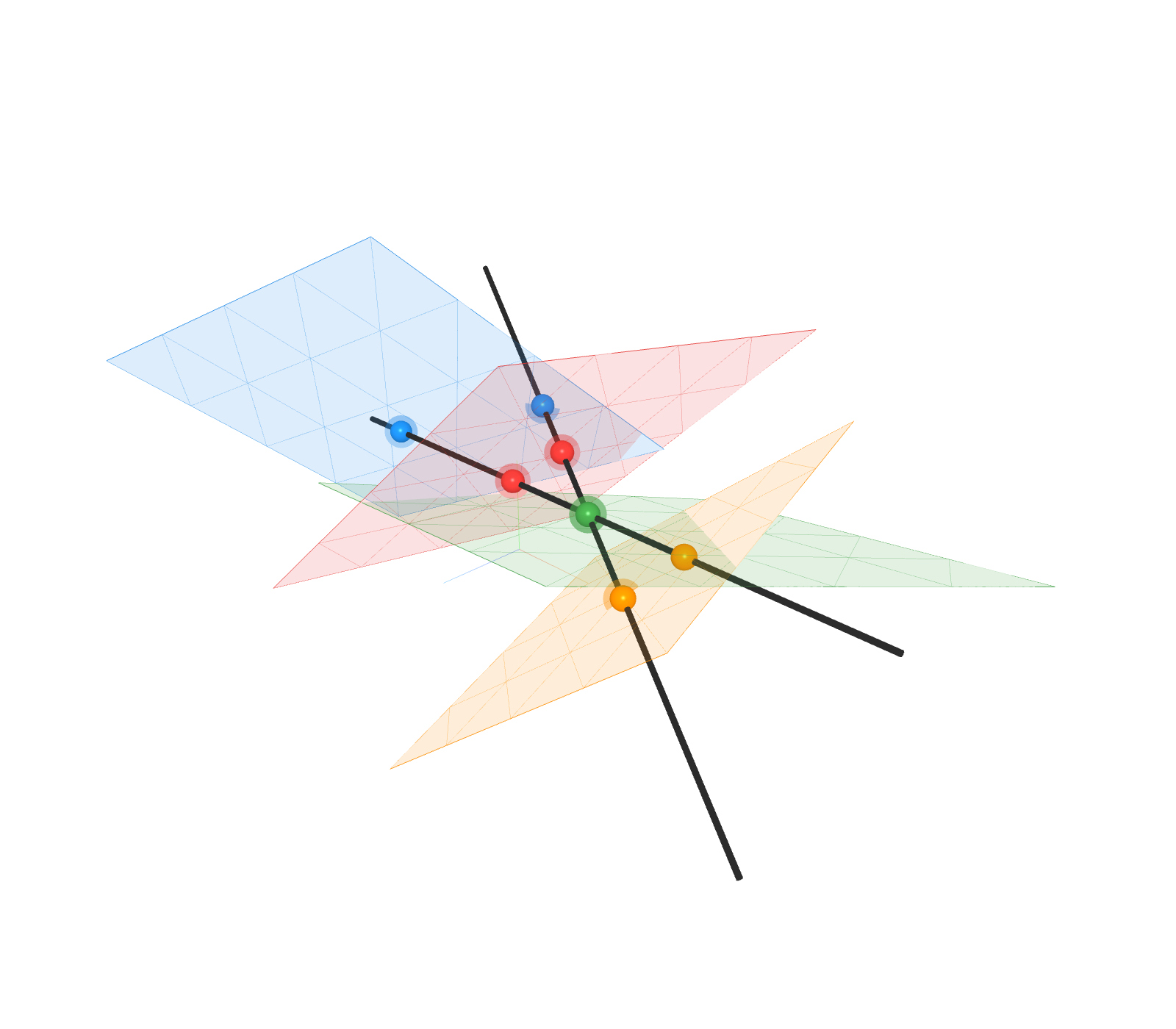
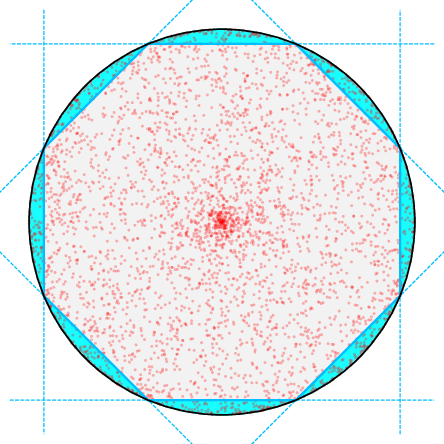
Figure 1: Visualization of data shatterability: (a) knots as learned representations on mixtures of lines; (b) more caps (high shatterability); (c) fewer caps (low shatterability).

The authors formalize shatterability via the data-dependent weight function $g$, which penalizes neurons that activate on small fractions of the data. In low-shatterability regimes, neurons must activate on large portions of the data to introduce nonlinearity, enforcing robust, shared representations. In high-shatterability regimes, neurons can specialize to isolated regions, facilitating memorization.

Main Theoretical Results

Adaptation to Intrinsic Low-Dimensionality

For data supported on a mixture of $J$ $m$-dimensional subspaces, the generalization gap for BEoS solutions is bounded by

$\tilde{O}\left(n^{-\frac{1}{2m+4}}\right)$

where the rate adapts to the intrinsic dimension $m$ and is only mildly dependent on $J$ and $d$. The proof leverages a decomposition of the global data-dependent weight function into local constraints on each subspace, showing that the implicit regularization is adaptive to the data geometry.

Spectrum of Generalization on Isotropic Distributions

For isotropic $\alpha$-powered-radial distributions, the generalization rate smoothly degrades as $\alpha$ decreases (i.e., as data concentrates toward the sphere):

$$\tilde{O}\left(n^{-\frac{2\alpha}{d-1+2\alpha}}\right)$$

In the limit $\alpha \to 0$ (data on the sphere), the lower bound matches the upper bound, and the network can interpolate the training data with stable solutions, demonstrating that stability alone does not preclude memorization.

Flat Interpolation on the Sphere

The authors construct explicit width-$n$ networks that perfectly interpolate any dataset supported on the sphere, with Hessian operator norm bounded by $1 + \frac{D^2+2}{n}$, showing that the BEoS condition is insufficient to guarantee generalization in highly shatterable regimes.

Empirical Validation

The theoretical predictions are validated through extensive experiments:

• Synthetic Data: Training two-layer ReLU networks on unions of lines (low-dimensional mixtures) yields generalization rates that are invariant to ambient dimension $d$, confirming adaptation to intrinsic dimension. For isotropic distributions, increasing $\alpha$ (less boundary concentration) improves generalization rates.
• Neuron Activation Statistics: On the sphere, most neurons fire on less than $10\%$ of the data, indicating highly specialized, memorizing units. On low-dimensional mixtures, neurons exhibit broader activation, reflecting feature reuse.

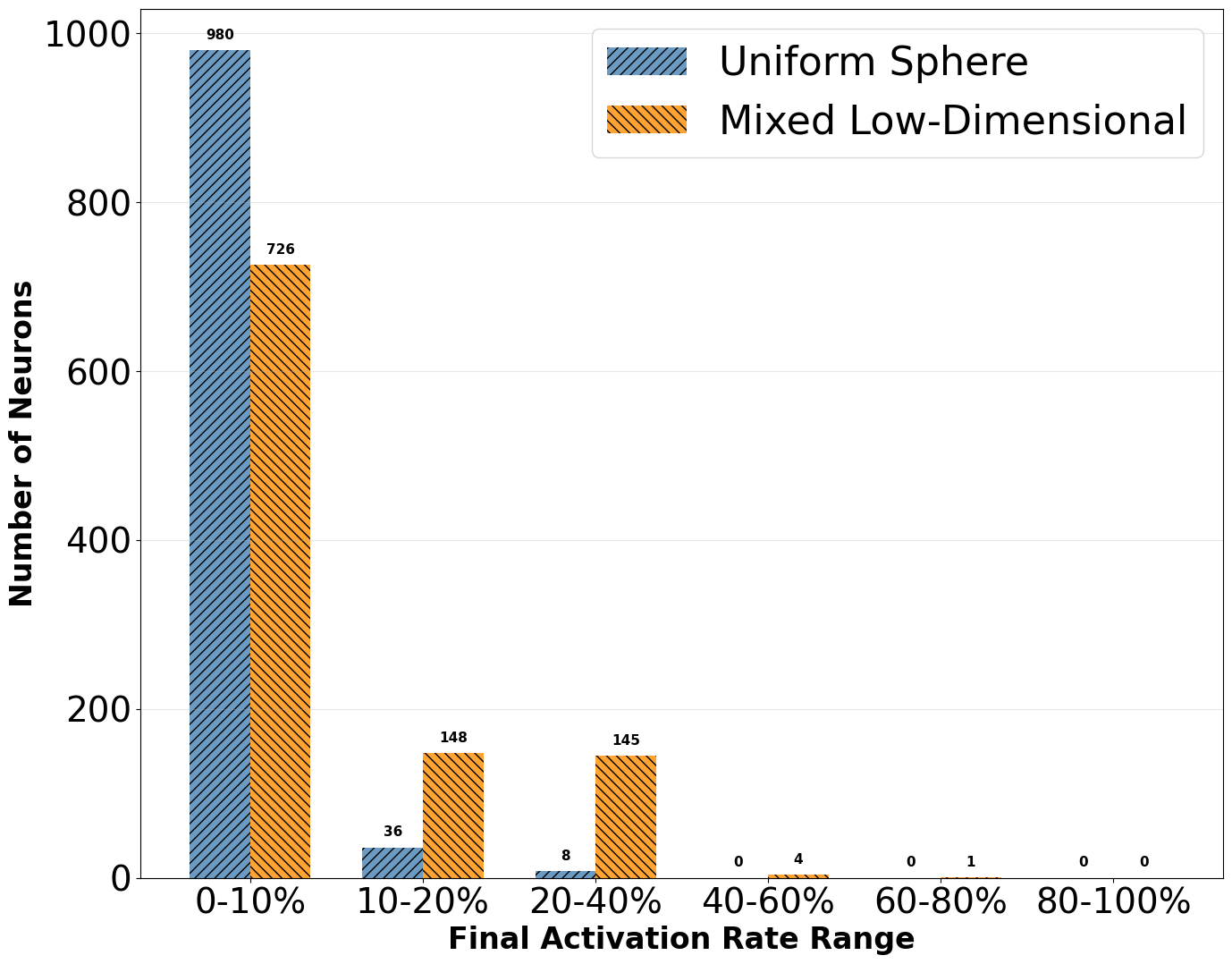
Figure 2: Neuron activation statistics: (a) sphere—specialized neurons; (b) low-dimensional mixture—broader activation.

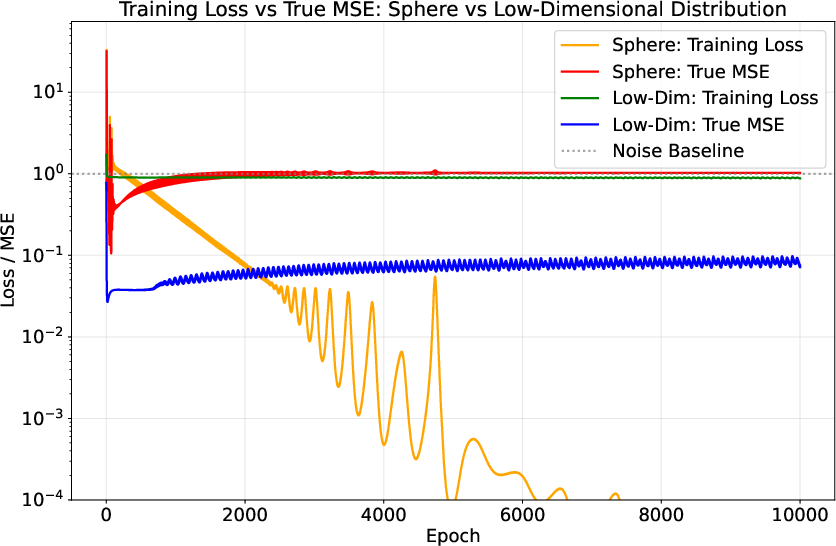
• Real Data (MNIST vs. Gaussian): GD on MNIST resists overfitting for orders of magnitude more iterations compared to Gaussian inputs, demonstrating the practical impact of low-dimensional structure on generalization.

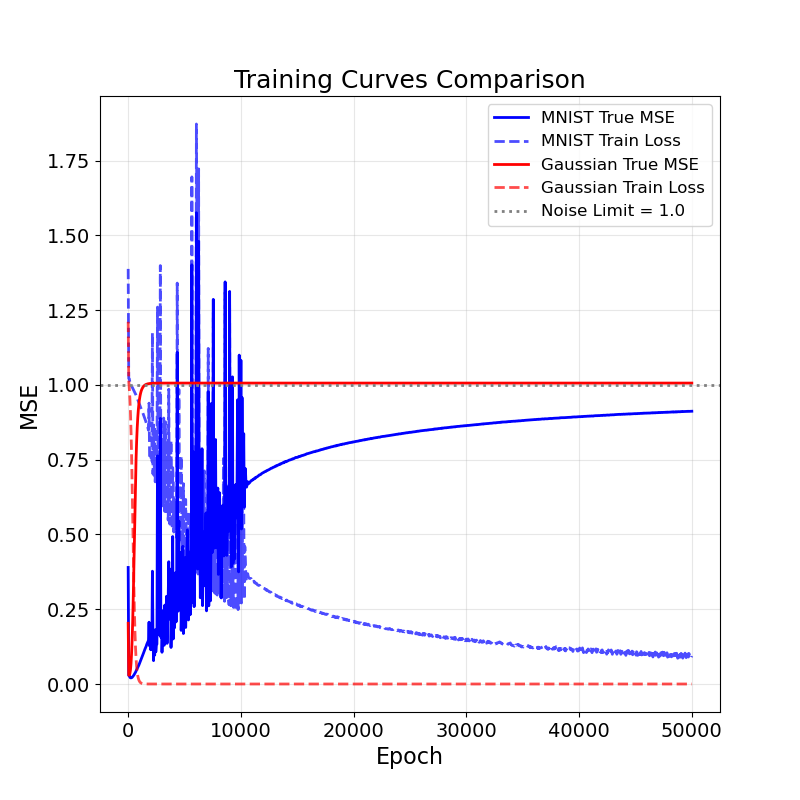
Figure 3: Data geometry and memorization on MNIST: left—training curves; right—prediction error vs. Tukey depth (shallow points have larger errors).

• Training Curves on Different Geometries: GD interpolates quickly on the sphere but resists overfitting on low-dimensional mixtures.

  Figure 4: Training loss and clean MSE on sphere vs. low-dimensional mixture.

Implications and Future Directions

The results consolidate and extend prior empirical and theoretical findings on implicit regularization, minima stability, and the role of data geometry in deep learning. The principle of data shatterability provides a unifying explanation for when and why GD discovers generalizable solutions in overparameterized networks. The analysis suggests that architectural inductive biases (e.g., CNNs), data augmentation (e.g., mixup), and activation-based pruning can be understood through their effects on shatterability.

The framework opens several avenues for future research:

• Quantifying shatterability for real-world data and representations in deep networks.
• Extending the analysis to deeper architectures and convolutional structures.
• Investigating the relationship between shatterability, optimization speed, and normalization techniques.
• Developing practical metrics and regularization strategies based on shatterability.

Conclusion

This paper establishes a rigorous connection between data geometry and generalization in overparameterized neural networks trained below the edge of stability. The principle of data shatterability governs the implicit bias of gradient descent, determining whether stable solutions generalize or memorize. Theoretical bounds, constructive lower bounds, and empirical evidence collectively demonstrate that low-shatterability geometries enforce robust, shared representations, while high-shatterability geometries permit memorization even under stability constraints. These insights have significant implications for the design and analysis of neural architectures, optimization algorithms, and data augmentation strategies in modern machine learning.