Papers
Topics
Authors
Recent
Assistant
AI Research Assistant
Well-researched responses based on relevant abstracts and paper content.
Custom Instructions Pro
Preferences or requirements that you'd like Emergent Mind to consider when generating responses.
Gemini 2.5 Flash
Gemini 2.5 Flash 162 tok/s
Gemini 2.5 Pro 51 tok/s Pro
GPT-5 Medium 31 tok/s Pro
GPT-5 High 28 tok/s Pro
GPT-4o 95 tok/s Pro
Kimi K2 202 tok/s Pro
GPT OSS 120B 425 tok/s Pro
Claude Sonnet 4.5 36 tok/s Pro
2000 character limit reached

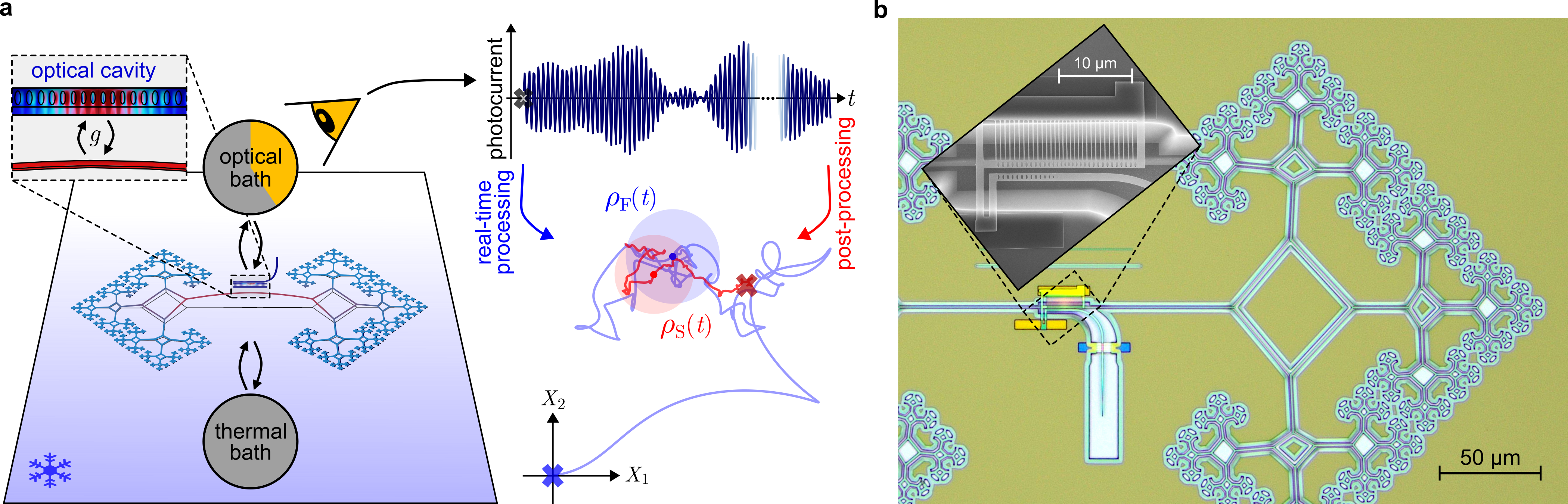
Post-processed estimation of quantum state trajectories (2510.16754v1)

Published 19 Oct 2025 in quant-ph

Abstract: Weak quantum measurements enable real-time tracking and control of dynamical quantum systems, producing quantum trajectories -- evolutions of the quantum state of the system conditioned on measurement outcomes. For classical systems, the accuracy of trajectories can be improved by incorporating future information, a procedure known as smoothing. Here we apply this concept to quantum systems, generalising a formalism of quantum state smoothing for an observer monitoring a quantum system exposed to environmental decoherence, a scenario important for many quantum information protocols. This allows future data to be incorporated when reconstructing the trajectories of quantum states. We experimentally demonstrate that smoothing improves accuracy using a continuously measured nanomechanical resonator, showing that the method compensates for both gaps in the measurement record and inaccessible environments. We further observe a key predicted departure from classical smoothing: quantum noise renders the trajectories nondifferentiable. These results establish that future information can enhance quantum trajectory reconstruction, with potential applications across quantum sensing, control, and error correction.

Summary

  • The paper presents a post-processing quantum state smoothing technique that leverages both past and future measurements to improve the accuracy and purity of state trajectories.
  • It employs homodyne detection on a nanomechanical resonator and linear-Gaussian quantum models to reduce uncertainty, achieving up to a six-fold variance reduction and a 23% lower Hilbert-Schmidt distance.
  • The study differentiates quantum from classical smoothing, underscoring its potential benefits for quantum sensing, control, and error correction applications.

Post-Processed Estimation of Quantum State Trajectories

Introduction

This work presents a rigorous experimental and theoretical investigation into quantum state smoothing, a post-processing technique that leverages both past and future measurement data to reconstruct quantum trajectories with enhanced accuracy. The paper generalizes the quantum state smoothing formalism to the scenario of a single observer monitoring an open quantum system subject to environmental decoherence, a configuration relevant to quantum information protocols, sensing, and control. The experimental validation is performed using a high-quality nanomechanical resonator coupled to an optical cavity, with continuous weak measurement implemented via homodyne detection. The results demonstrate that smoothing yields quantum state trajectories with reduced uncertainty and increased purity, outperforming conventional filtering approaches and classical smoothing analogs. Figure 1

Figure 1: Schematic of the experimental setup and phase-space illustration of real-time (blue) and post-processed (red) quantum trajectories for a nanomechanical resonator under continuous optical monitoring.

Quantum State Smoothing Formalism

Quantum trajectories under continuous weak measurement are typically reconstructed in real time using filtering, which conditions the system's state on the measurement record up to the present. However, filtering is limited by the finite duration of the available record, especially in the transient regime following the onset of monitoring. Smoothing, by contrast, incorporates both past and future data, enabling more accurate estimation of the system's state at any given time.

The formalism is extended from the two-observer scenario of Guevara and Wiseman (2015) to a sequential single-observer case, where the observer's record is used to optimally estimate the long-time-limit (LTL) filtered state. For linear-Gaussian quantum (LGQ) systems, the smoothed state is characterized by the first and second moments of the phase-space operators, with the optimal estimate minimizing the Hilbert-Schmidt distance to the LTL filtered state. The explicit update equations for the smoothed moments are derived, generalizing previous results to accommodate inaccessible environmental information and transient initial conditions.

Experimental Implementation

The experimental platform consists of a silicon nitride nanomechanical resonator coupled to a photonic crystal cavity, enabling quantum-limited readout of mechanical motion via homodyne detection. The system is engineered for high optomechanical cooperativity and detection efficiency, with the resonator cooled to cryogenic temperatures to suppress thermal noise. The measurement record is demodulated to extract the mechanical quadratures, and the filtering and retrofiltering equations are applied to reconstruct the quantum trajectories. Figure 2

Figure 2: Fluctuations of the quadrature mean value traces, showing the autocorrelation of the "velocity" for quantum filtering, quantum smoothing, and classical smoothing.

The analysis reveals that smoothing yields mean values and variances that are closer to the LTL filtered state than filtering alone, particularly in the transient regime. The smoothed state exhibits higher purity, with the variance reduced by up to a factor of six at the onset of monitoring. The accuracy is quantified using the ensemble-averaged squared Hilbert-Schmidt distance, with smoothing consistently outperforming filtering.

Estimation of the "True" Quantum State

In realistic scenarios, not all environmental baths are accessible to measurement, rendering the LTL filtered state impure. The paper generalizes the smoothing formalism to estimate the "true" quantum state, conditioned on hypothetical measurements of all baths. The natural unravelling for the unobserved baths is identified as heterodyne detection, yielding a stochastic coherent state as the true trajectory.

Experimental validation is achieved by artificially reducing the detection efficiency via noise injection, simulating the presence of an unobserved bath. The smoothed estimate tracks the LTL filtered state more closely than the filtered estimate, with a 23% reduction in Hilbert-Schmidt distance at the record start and 13% in steady state. This demonstrates that post-processing can partially compensate for measurement inefficiency and noise-induced degradation.

(Figure 3)

Figure 3: Trajectories after noise injection, illustrating the effect of reduced detection efficiency on the accuracy of filtered and smoothed quantum state estimates.

Quantum vs. Classical Smoothing

A key theoretical and experimental result is the fundamental distinction between quantum and classical smoothing. While the filtering equations for LGQ systems are formally identical to their classical counterparts, quantum smoothing incorporates non-commuting future observables, resulting in nondifferentiable, stochastic trajectories. Classical smoothing yields smooth mean value traces, but when applied to quantum systems, it can produce unphysical states with variances below the Heisenberg limit.

The autocorrelation analysis of the quadrature velocities confirms that quantum smoothing exhibits rapid decorrelation, in contrast to the sustained correlations of classical smoothing. The classical smoothing variances are consistently lower than those of quantum smoothing and filtering, indicating apparent violations of the uncertainty principle in the semiclassical regime. Furthermore, classical smoothing yields inferior accuracy in estimating the quantum state, as evidenced by larger Hilbert-Schmidt distances.

Implications and Future Directions

The demonstrated ability of quantum state smoothing to enhance trajectory reconstruction has significant implications for quantum sensing, control, and error correction. In sensing applications, smoothing can improve precision by mitigating noise and compensating for measurement inefficiency. In quantum error correction, post-processing with future data may reduce resource requirements for information storage. The formalism is particularly relevant for protocols exploiting transient conditional dynamics, enabling earlier and higher-fidelity preparation of non-classical states.

The work also raises foundational questions regarding the nature of quantum state trajectories and decoherence, highlighting the dependence of the reconstructed state on the physical model of system-environment interactions. The incompatibility of classical smoothing with quantum state estimation underscores the necessity of quantum-specific post-processing techniques.

Conclusion

This paper establishes quantum state smoothing as a robust method for post-processed estimation of quantum trajectories, providing enhanced accuracy and purity over conventional filtering and classical smoothing approaches. The experimental results validate the theoretical predictions, demonstrating the utility of smoothing in realistic quantum systems subject to environmental decoherence and measurement inefficiency. The formalism and experimental techniques developed herein are broadly applicable to quantum information, sensing, and control, and motivate further exploration of optimal estimation strategies in open quantum systems.

File Document Download Save Streamline Icon: https://streamlinehq.com PDF File Document Download Save Streamline Icon: https://streamlinehq.com Markdown
Ai Generate Text Spark Streamline Icon: https://streamlinehq.com

Explain it Like I'm 14

Overview

This paper is about a smarter way to figure out how a quantum system changes over time. In simple terms, the authors show that if you’re watching a tiny vibrating object (a nanomechanical resonator) and your measurements are a bit noisy or incomplete, you can use information from the future to improve your understanding of what happened earlier. This trick is called “smoothing.” They adapt smoothing to work for quantum systems and test it in a real experiment.

Key Objectives

The paper sets out to answer three big, easy-to-understand questions:

  • Can using future measurements help us reconstruct past quantum states more accurately?
  • Does smoothing help even when some information about the system leaks into parts of the environment we can’t measure?
  • How is “quantum smoothing” different from ordinary (classical) smoothing?

How Did They Do It?

Think of watching a blurry video of a bouncing ball. If you only look at frames up to the current moment, your best guess of the ball’s path might be off. But if you also look at frames that come after, you can make a better estimate of where the ball was earlier. That’s smoothing.

Here’s how the team applied this idea to a quantum system:

  • They used a tiny, high-quality mechanical resonator (like a microscopic drum) that vibrates at about 1 MHz.
  • Light from a laser bounces off a special optical cavity attached to this resonator. The light carries information about the resonator’s motion.
  • A “weak measurement” means they gently measure the system continuously, so they don’t completely disturb it. The measurements are noisy, like listening to a sound through static.
  • They collected a stream of measurement data and created two kinds of estimates:
    • Filtering: using only past data (up to the current time).
    • Smoothing: using both past and future data from the full record.
  • They compared these estimates to two targets:
    • The “long-time-limit (LTL) filtered state”: what you would get if you had started measuring a long time ago and kept going continuously.
    • The “true state”: what you would get if you could measure everything the system interacts with (including the parts of the environment you usually can’t access), which is typically pure and very well-defined.
  • They also did a clever test where they added extra electronic noise to their measurements on purpose. This simulated having worse measurement efficiency, like turning down the brightness of that blurry video, and checked whether smoothing still helps.

Main Findings

The authors found several important things:

  • Smoothing improves accuracy. When they used future data, their estimates of the quantum state matched the targets more closely than when using past data alone. This was especially helpful right after measurements began (the “transient” period) when information is still being gathered.
  • Smoothing helps even with missing information. In real life, some information about a quantum system is lost to the environment. Smoothing still improved the estimates, partly “making up” for gaps or inaccessible parts of the environment.
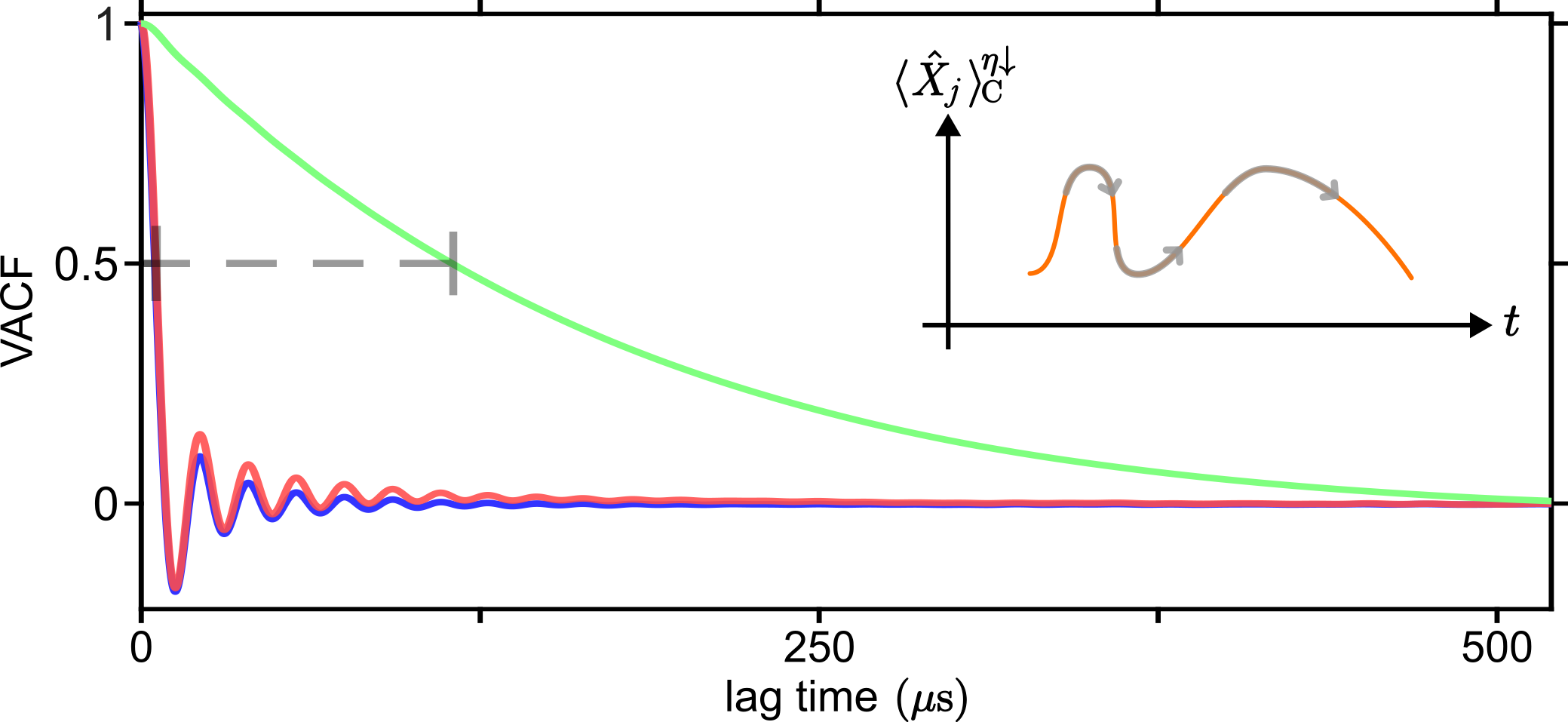
  • Quantum smoothing is not smooth. In classical smoothing (like tracking a car’s position), the smoothed path is usually a smooth curve. But quantum systems have unavoidable randomness (quantum noise). Even after smoothing, the estimated quantum trajectories look “jittery” — their time derivatives don’t behave smoothly. The team confirmed this by measuring how rapidly the smoothed values change over time compared to classical smoothing, which stays much smoother.
  • Classical smoothing can be misleading for quantum systems. When they applied classical smoothing formulas to this quantum problem, they got estimates that look very neat but can actually become unphysical (for example, seeming to beat quantum uncertainty limits if pushed far enough). These classical estimates were also less accurate at matching the targets than the proper quantum smoothing method.
  • Noise reduction by post-processing works. In the noise-added experiment, using future data lowered the mismatch between the estimate and the target by up to about 23% at the start and 13% in steady operation. This shows smoothing can recover some precision lost to noise or lower measurement efficiency.

Why It Matters

  • Better sensing and control: Many quantum devices rely on continuous, gentle measurements to sense signals or to keep a system in a desired state. Smoothing lets you use future data to sharpen your view of the past, which can improve precision and stability.
  • Helps with error correction: Quantum computers need error correction. Some methods use post-processing of measurement records. Smoothing suggests you could store less past data by relying on future data to reach the same accuracy, potentially saving memory and processing resources.
  • Works in realistic conditions: Real quantum systems always interact with environments we can’t fully measure. This method shows you can still improve your estimates even when you don’t see everything.
  • Foundational insights: The work highlights a deep difference between classical and quantum worlds. Even after “smoothing,” quantum trajectories remain fundamentally jittery because of quantum noise. This connects to big ideas like time symmetry and decoherence (how quantum systems lose their “quantumness” to their surroundings).

In short, the paper shows that future information can help reconstruct past quantum states more accurately, even in the messy real world, and that quantum smoothing behaves in a fundamentally different way from classical smoothing. This opens the door to better quantum sensing, control, and error correction, and sheds light on the nature of quantum dynamics.

Ai Sparkles Streamline Icon: https://streamlinehq.com View Paper Prompt List Streamline Icon: https://streamlinehq.com View All Prompts
Ai Generate Text Spark Streamline Icon: https://streamlinehq.com

Knowledge Gaps

Knowledge gaps, limitations, and open questions

Below is a single, concrete list of what remains missing, uncertain, or unexplored, as actionable directions for future research:

  • Generality beyond linear-Gaussian systems: The formalism and experiment target single-mode linear-Gaussian (LGQ) dynamics; extension to non-Gaussian states, nonlinear systems, and discrete-variable systems (e.g., qubits, superconducting circuits) remains untested experimentally and only partially treated theoretically.
  • Multi-mode and entangled systems: It is unknown how quantum state smoothing performs for multi-mode, entangled, or networked systems, including whether smoothing reliably reconstructs entanglement trajectories and cross-mode correlations.
  • Non-Markovian environments: The theory assumes Markovian baths; performance and correctness under non-Markovian dynamics, environmental memory, or colored process noise are not addressed.
  • Choice and inference of “true” unravelling: The “natural” unravelling for unobserved baths is assumed (heterodyne) under specific symmetry and Markovian criteria; methods to identify, test, or learn the physically correct unravelling from data, and the impact of alternative unravelings (e.g., photon counting, homodyne of different quadratures) on smoothed trajectories and purity, are open.
  • Direct validation of the true-state estimate: The experiment cannot access the mean values of the pure “true” state; developing schemes to probe or emulate the unobserved baths (e.g., auxiliary probes, engineered measurement of the environment) to directly validate true-state trajectories is an open challenge.
  • Robustness to model mismatch and parameter drift: Smoothing relies on accurate knowledge of η\eta, Γ\Gamma, nthn_\text{th}, C\mathcal{C}, and the fast-cavity/adiabatic approximations; robustness to miscalibration, time-varying parameters, and modeling errors is not characterized.
  • Adaptive and joint parameter estimation: There is no integrated framework for simultaneously smoothing the state and estimating unknown system or noise parameters (e.g., η\eta, Γ\Gamma, nthn_\text{th}) online; quantifying performance under adaptive identification is needed.
  • Real-time (fixed-lag) implementations: Smoothing is performed offline; developing low-latency fixed-lag quantum smoothers compatible with feedback control and error correction loops (with explicit resource and hardware constraints) remains open.
  • Integration with measurement-based feedback: Feedback is treated effectively via modified rates; explicit inclusion of feedback dynamics and feedback-induced correlations in the stochastic models, and their effect on smoothing performance, is not explored.
  • Handling measurement record gaps: Although smoothing is claimed to compensate for gaps, experiments do not explicitly test missing-data scenarios; gap-aware algorithms and quantitative performance under dropouts are needed.
  • Quantitative performance bounds: General bounds linking smoothing improvements (e.g., reduction in Hilbert–Schmidt distance, purity gain) to η\eta, C/nth\mathcal{C}/n_\text{th}, record length, and noise spectra are not derived; scaling laws and limits (e.g., as η→0\eta \to 0 or η→1\eta \to 1) are missing.
  • Nondifferentiability characterization: The nondifferentiability of quantum-smoothed trajectories is verified indirectly via autocorrelation of derivative; operational metrics (e.g., Hölder exponents, path regularity statistics) and regimes where exceptions occur need systematic paper.
  • Classical smoothing breakdown: The predicted “apparent violation” of the Heisenberg uncertainty principle by classical smoothing requires η>0.25\eta>0.25 and C/nth>1/(4η−1)\mathcal{C}/n_\text{th} > 1/(4\eta-1); an experimental demonstration at parameters meeting both conditions is outstanding.
  • Equivalence of electronic noise and optical inefficiency: Noise-injection is used to emulate reduced η\eta; validating the asserted quantitative equivalence with controlled optical loss (mixing with vacuum) and assessing differences (e.g., noise spectra, correlations) are open.
  • Fast-cavity and demodulation assumptions: The analysis assumes the fast-cavity limit and demodulates at Ω\Omega, neglecting fast dynamics; verifying performance in the sideband-resolved regime and under frequency-dependent coupling is needed.
  • Record-length and windowing effects: Smoothing is performed on 750 µs segments; optimizing window length and evaluating how benefits scale with segment duration and start/end boundary effects (especially near record endpoints) is not addressed.
  • Alternative distance and task metrics: The paper uses squared Hilbert–Schmidt distance and notes relative entropy gives the same optimum; benchmarking with fidelity, trace distance, and task-specific metrics (e.g., force/phase estimation error) is missing.
  • Task-level gains: Demonstrations of improved sensing precision or control performance (beyond state-distance metrics), especially in force tracking, phase estimation, or quantum error correction benchmarks, are absent.
  • Computational scalability: The complexity and memory requirements of smoothing for high-dimensional systems and long records are not analyzed; efficient approximate algorithms and resource–accuracy trade-offs are open.
  • Learning and testing environmental “naturalness” criteria: The adopted invariance and Markovian criteria for natural unravelling may not be unique in general; frameworks to test and compare “naturalness” hypotheses against data are lacking.
  • Colored noise and higher-mode coupling: Performance is limited by colored noise from higher mechanical resonances at large nˉcav\bar{n}_\text{cav}; smoothing methods that explicitly model and mitigate colored measurement/process noise, and device designs to reduce mode competition, are needed.
  • Uncertainty in covariance estimation: Conditional variances cannot be measured directly and are inferred via ensemble relations; developing direct or indirect validation protocols, and quantifying bias when the model is imperfect, is an open methodological issue.
Ai Sparkles Streamline Icon: https://streamlinehq.com View Paper Prompt List Streamline Icon: https://streamlinehq.com View All Prompts
Ai Generate Text Spark Streamline Icon: https://streamlinehq.com

Practical Applications

Below is an overview of the paper’s practical implications, focusing on how its findings, methods, and innovations translate into deployable use cases. The core contribution is a generalized quantum state smoothing framework for single-observer continuous measurements in open quantum systems, together with an experimental demonstration on a strongly monitored nanomechanical resonator. The results show that post-processing with future data yields more accurate quantum state trajectories, compensates for missing or noisy data, and reveals fundamentally quantum features (nondifferentiable trajectories) that distinguish quantum from classical smoothing.

Immediate Applications

  • Post-processed trajectory reconstruction in existing continuous-measurement experiments
    • Sector: academia; quantum hardware vendors (optomechanics, superconducting circuits, spin qubits, atomic ensembles)
    • What it enables: more accurate state estimates during transient and steady-state operation by fusing past and future data; up to 3× better initial mean-value accuracy and ~6× higher initial purity for LTL targets; 23%–13% lower distance to target state under added noise (start/steady state)
    • Tools/workflows: add a smoothing stage to existing filtering pipelines (forward–backward pass: filter, retrofilter, combine via provided LGQ equations); integrate into Python/MATLAB control stacks (e.g., QuTiP-based, LabVIEW)
    • Assumptions/dependencies: system well-modeled as linear-Gaussian (LGQ) with calibrated parameters; sufficient detection efficiency; recorded measurement histories; near-Markovian baths; tolerance for post-run (not real-time) analysis
  • Gap and inefficiency compensation in quantum sensing via post-processing
    • Sector: quantum sensing (optomechanical force/acceleration sensors, atomic magnetometers), precision metrology; early-stage gravitational-wave and dark-matter detection prototypes
    • What it enables: partial recovery from missing data or reduced detection efficiency (η↓); “virtual efficiency boost” demonstrated by additive-noise tests
    • Tools/workflows: noise-aware smoothing that treats added white noise as effective η reduction; quality checks using ensemble relations and Hilbert–Schmidt distance metrics
    • Assumptions/dependencies: noise approximately white/stationary over the window; accurate sensor model; availability of future data buffers
  • Faster, higher-fidelity state preparation and characterization in the transient regime
    • Sector: quantum control and state engineering (entanglement/squeezing protocols)
    • What it enables: earlier achievement of useful conditional states by leveraging future information; improved fidelity of prepared states
    • Tools/workflows: windowed smoothing over short records following the start of monitoring; shortened experimental cycles
    • Assumptions/dependencies: negligible penalty for post-selection/post-processing latency; stable calibration
  • Improved offline evaluation and development of feedback controllers and decoders
    • Sector: quantum computing (continuous-readout error detection/correction), control engineering for quantum hardware
    • What it enables: better training labels for machine learning controllers/decoders using smoothed trajectories; offline benchmarking of feedback strategies against more accurate ground truths
    • Tools/workflows: supervised learning with smoothed trajectories as targets; comparison of filtered vs smoothed performance curves
    • Assumptions/dependencies: post-processing acceptable; controller retraining cycles available
  • Diagnostics and model validation for continuous-measurement setups
    • Sector: academia; quantum device characterization
    • What it enables: consistency checks (variance difference equals conditional variance), detection of model mis-specification, and verification of quantum vs classical behavior (e.g., nondifferentiable trajectory signatures via velocity autocorrelation)
    • Tools/workflows: ensemble-based checks (variance–mean relations), Hilbert–Schmidt distance monitoring, quadrature-velocity autocorrelation analysis
    • Assumptions/dependencies: sufficiently large ensembles of records; stable operating conditions
  • Foundational and thermodynamic studies using purer conditional states
    • Sector: academia (quantum foundations, time symmetry, conditional entropy production)
    • What it enables: reduced estimator bias in studies of time-symmetric formulations, entropy production under continuous measurement, and trajectory-level phenomena
    • Tools/workflows: replace filtered trajectories with smoothed ones in analysis; compare classical vs quantum smoothing predictions
    • Assumptions/dependencies: well-defined unravelling assumptions for “true state” estimates; careful interpretation of conditionality

Long-Term Applications

  • Near-real-time smoothed feedback control (time-symmetric estimation with bounded latency)
    • Sector: quantum control; high-performance sensing/control hardware
    • What it could enable: performance beyond standard Kalman-like feedback by exploiting short look-ahead buffers; improved stabilization and disturbance rejection
    • Tools/products: FPGA/ASIC implementations of forward–backward filters; low-latency memory for rolling buffers; integration into commercial control electronics
    • Assumptions/dependencies: latency acceptable relative to system timescales; computational and I/O budgets met; robustness to modest model drift
  • Enhanced continuous quantum error correction via time-symmetric decoding
    • Sector: quantum computing (cat/surface-code variants with continuous readout)
    • What it could enable: lower logical error rates or reduced buffer requirements by trading stored past data for short future windows; improved post-processed decoding
    • Tools/products: syndrome-processing firmware/accelerators that implement smoothing; time-windowed decoders leveraging future syndromes
    • Assumptions/dependencies: architectures tolerate decoding delays; scalable memory/computation; compatibility with code cycle times
  • “Software efficiency upgrade” for quantum sensors
    • Sector: sensing/metrology (navigation-grade optomechanical inertial sensors; seismology; precision force probes)
    • What it could enable: improved SNR and effective detection efficiency through embedded smoothing in device firmware; better performance without hardware redesign
    • Tools/products: OEM firmware updates with smoothing pipelines; calibration routines that auto-tune model parameters for optimal smoothing
    • Assumptions/dependencies: stable system identification; stationarity over smoothing window; certification procedures that accept post-processing gains
  • Channel and state tracking in quantum communication
    • Sector: quantum communications/networks (continuous-variable systems)
    • What it could enable: improved channel estimation and state tracking at receivers using time-symmetric processing, yielding better reconciliation and error mitigation
    • Tools/products: receiver-side smoothing libraries; batch-mode decoders with look-ahead windows
    • Assumptions/dependencies: Gaussian channel approximations; buffer/latency acceptable in application; secure handling of stored records
  • Standards and policy for measurement-record retention and benchmarking
    • Sector: standards bodies (e.g., NIST/ISO), funding agencies, consortia
    • What it could enable: guidelines requiring retention/sharing of raw records and metadata to enable smoothing; benchmark protocols that report both filtered and smoothed sensitivity/accuracy; definitions of LTL and “true-state” target scenarios
    • Tools/workflows: standardized data formats and metadata (calibration, detection efficiency, model parameters); reference datasets with smoothed baselines
    • Assumptions/dependencies: community consensus on unravelling conventions and reporting; privacy/IP considerations for sharing raw data
  • Certification and diagnostics via nondifferentiable trajectory signatures
    • Sector: metrology/standards; hardware QA
    • What it could enable: routine tests that distinguish quantum from classical smoothing (e.g., velocity autocorrelation times), certifying genuine quantum backaction and model adequacy
    • Tools/workflows: automated VACF analysis and hypothesis testing integrated into device commissioning
    • Assumptions/dependencies: sufficient bandwidth/resolution; minimal classical correlated noise
  • Adaptive experiment design and Hamiltonian learning with smoothed feedback between runs
    • Sector: academia/industrial R&D in quantum characterization and control
    • What it could enable: faster, more accurate parameter learning and adaptive protocols using higher-fidelity trajectory estimates as inputs to the next batch
    • Tools/workflows: Bayesian/ML estimators that ingest smoothed trajectories; closed-loop experiment managers
    • Assumptions/dependencies: batch-mode or interleaved operation; computational resources to keep pace with run cadence

Cross-cutting assumptions and dependencies to consider for all applications:

  • Model fidelity: smoothing relies on accurate system identification (rates, efficiencies, noise models) and usually on linear-Gaussian, Markovian approximations.
  • Unravelling choice: “true state” estimation depends on assumptions about unobserved-bath measurements (here, a unique “natural” heterodyne unravelling for the symmetric master equation). Different environments imply different target sets.
  • Data handling: smoothing needs access to future data; buffer sizes and latency constraints dictate whether usage is offline, batch, or near-real-time.
  • Computation and storage: forward–backward passes over high-rate data require sufficient memory and compute; hardware acceleration may be needed for low-latency deployments.
  • Compliance with quantum limits: smoothing does not violate Heisenberg limits; classical smoothing applied to quantum data can yield unphysical estimates—use quantum-consistent equations.

Overall, the paper provides a ready-to-use post-processing method for immediate accuracy gains in continuous quantum measurements, and it suggests a path to next-generation control, sensing, and error-correction workflows that explicitly leverage time-symmetric estimation.

Ai Sparkles Streamline Icon: https://streamlinehq.com View Paper Prompt List Streamline Icon: https://streamlinehq.com View All Prompts
Ai Generate Text Spark Streamline Icon: https://streamlinehq.com

Glossary

  • Adiabatically eliminated: A modeling approximation where fast subsystem dynamics are removed, leaving an effective description for slower variables. "The combined optomechanical system is well inside the fast-cavity limit, so that the cavity dynamics can be adiabatically eliminated."
  • Autocorrelation function: A function quantifying how a signal correlates with itself over time delays; here used for the time derivative of quadrature means. "The quadrature “velocity" (⟨X^j⟩Cη↓/t)(\langle\hat{X}_j\rangle_\text{C}^{\eta\downarrow}/ t) autocorrelation function (VACF) for filtering (blue), quantum state smoothing (red) and classical smoothing (green)."
  • Bath: An environment (optical or thermal) that exchanges information and/or energy with a system, inducing noise and decoherence. "Each bar represents all the baths as a whole that continuously interacts with the resonator."
  • Cavity optomechanical systems: Platforms where optical fields interact with mechanical motion via radiation pressure, enabling quantum-limited measurement and control. "Cavity optomechanical systems --- where an optical probe enables quantum-limited readout of mechanical motion --- offer an important platform for achieving this regime."
  • Canonical operators: Fundamental position and momentum operators that satisfy canonical commutation relations. "contains the canonical operators for position q^j\hat{q}_j and momentum p^j\hat{p}_j"
  • Coherent state: A minimum-uncertainty quantum state (like a displaced ground state) often used to model classical-like behavior in quantum systems. "Considering the total unravelling, the true state of the system is a stochastic coherent state (that is, the ground state with a stochastic phase-space displacement)"
  • Decoherence: The loss of quantum coherence due to system-environment interactions. "exposed to environmental decoherence"
  • Demodulated: Signal processing step that extracts components at a target frequency; here used to obtain mechanical quadrature currents. "The photocurrent is normalized to the shot noise level and demodulated at mechanical frequency Ω\Omega."
  • Dilution refrigerator: An ultra-low-temperature cryogenic system used to cool devices near millikelvin regimes. "The device is placed in a dilution refrigerator to reduce nthn_\text{th}."
  • Dispersive coupling: An interaction where a system shifts the resonance frequency of a cavity, enabling readout via phase changes. "We monitor this resonance via dispersive coupling to a telecom-wavelength photonic crystal cavity with linewidth κ/2π=11.5\kappa/2\pi=11.5~GHz"
  • Evanescently coupled: Optical coupling via near-field evanescent waves between closely spaced structures. "the cavity is first evanescently coupled to an on-chip waveguide with efficiency ηesc=0.82\eta_\text{esc} = 0.82"
  • Fast-cavity limit: Regime where the cavity field responds much faster than mechanical motion, allowing simplifications in modeling. "The combined optomechanical system is well inside the fast-cavity limit"
  • Filtered state: The state estimate conditioned only on past measurement data up to the current time. "filtered state (inferred from past measurement data)"
  • Gaussian Wigner functions: Phase-space quasi-probability distributions with Gaussian form, fully characterized by means and covariances. "are the mean and covariance matrix of Gaussian Wigner functions inferred from the measurement record"
  • Heisenberg uncertainty principle: A fundamental quantum limit on simultaneous knowledge of conjugate observables like position and momentum. "apparent violation of the Heisenberg uncertainty principle"
  • Heterodyne detection: Measurement technique that simultaneously extracts both quadratures by mixing with a local oscillator offset in frequency. "The demodulation produces two measurement currents corresponding to heterodyne detection of the resonator’s quadratures"
  • Hilbert–Schmidt distance: A metric for distinguishability between quantum states, based on the Frobenius norm of their difference. "minimizes the squared Hilbert-Schmidt distance, ΔHS2[ρFLTL,ρC]=Tr[(ρFLTL−ρC)2]\Delta^2_\text{HS}[\rho_\text{F}^\text{LTL},\rho_\text{C}]=\text{Tr}[(\rho_\text{F}^\text{LTL}-\rho_\text{C})^2]."
  • Homodyne measurement: Quadrature measurement using interference with a phase-matched local oscillator to read out one quadrature at a time. "which we detect with efficiency η\eta using shot-noise-limited homodyne measurement"
  • Linear-Gaussian quantum (LGQ) systems: Systems whose dynamics and measurement processes preserve Gaussianity, enabling linear estimation theory. "we can use the formalism of linear-Gaussian quantum (LGQ) systems"
  • Long-time-limit (LTL) filtered state: The filtered state obtained when conditioning includes an effectively infinite past, removing transient effects. "long-time-limit (LTL) filtered state ρLTL(t)\rho^\text{LTL}(t)"
  • Markovian: Memoryless dynamics where future evolution depends only on the present state, not on past history. "which is effectively Markovian"
  • Master equation (stochastic): A differential equation governing the time evolution of a quantum state under open-system dynamics and measurement noise. "derived from the system's stochastic master equation"
  • Optical bath: The part of the environment composed of optical modes that couple to the system and carry away information. "interaction between the resonator and an optical bath."
  • Optomechanical cooperativity: Dimensionless parameter quantifying the strength of optomechanical interaction relative to mechanical damping. "where C=4nˉcavg02/(κΓ)\mathcal{C} = 4\bar{n}_\text{cav} g_0^2 / (\kappa \Gamma) is the optomechanical cooperativity."
  • Phase space: A geometric representation of a system’s state using conjugate variables (e.g., position and momentum). "diffuse in the rotating phase space spanned by mechanical quadratures X1,2X_{1,2}."
  • Photocurrent: The electrical current generated by photodetectors in response to incident light, used as the measurement record. "monitor the nanomechanical resonator for several seconds and record the homodyne photocurrent."
  • Photonic crystal cavity: A microcavity formed by periodic dielectric structures that confine light at specific frequencies. "a telecom-wavelength photonic crystal cavity with linewidth κ/2π=11.5\kappa/2\pi=11.5~GHz"
  • Ponderomotive squeezing: Quantum squeezing of light induced by radiation-pressure interaction with a mechanical oscillator. "we demonstrate ponderomotive squeezing of light by quantum backaction"
  • Quadrature: The cosine- and sine-weighted components of an oscillator’s position and momentum in a rotating frame. "quadratures, X^1=cos⁡(Ωt) q^−sin⁡(Ωt) p^\hat X_{1}=\cos(\Omega t)\,\hat q-\sin(\Omega t)\,\hat p and X^2=sin⁡(Ωt) q^+cos⁡(Ωt) p^\hat X_{2}=\sin(\Omega t)\,\hat q+\cos(\Omega t)\,\hat p"
  • Quantum backaction: Disturbance of a system's dynamics caused by the act of quantum measurement. "The resonator is subject to continuous monitoring which introduces significant quantum backaction."
  • Quantum state smoothing: Post-processing method that uses both past and future measurement data to improve quantum state trajectory estimates. "generalising a formalism of quantum state smoothing"
  • Retrofiltered effect operator: The operator inferred from future measurement outcomes, used in smoothing to combine with filtered estimates. "retrofiltered effect operator (inferred from future data)"
  • Shot-noise-limited: Operating regime where measurement noise is dominated by photon counting statistics rather than technical noise. "using shot-noise-limited homodyne measurement"
  • Smoothing (classical): Post-processing estimator that combines past and future data to reduce estimation error in classical systems. "classical smoothing typically results in differentiable trajectories"
  • Stochastic Schrödinger equation: A random (noise-driven) evolution equation for pure-state trajectories under continuous measurement. "Ideally, this state is pure and evolves according to a stochastic Schrödinger equation."
  • Unconditional variance: The variance of a system observable without conditioning on any measurement record. "where σuncon2\sigma^2_\text{uncon} is the unconditional variance"
  • Unravelling (natural unravelling): A particular measurement scheme applied to environmental channels that yields a specific stochastic trajectory consistent with the master equation. "there is a unique “unravelling” (type of measurement) which satisfies the following desiderata for naturalness"
  • Weak quantum measurements: Measurements that only partially collapse the quantum state, enabling continuous monitoring and control. "Weak quantum measurements enable real-time tracking and control of dynamical quantum systems"
  • Weak-values: Context-dependent averages obtained from weak measurements with pre- and post-selection, which can lie outside eigenvalue ranges. "It has been applied to generate trajectories of quantum weak-values"
Ai Sparkles Streamline Icon: https://streamlinehq.com View Paper Prompt List Streamline Icon: https://streamlinehq.com View All Prompts
Dice Question Streamline Icon: https://streamlinehq.com

Open Problems

  1. Characterize the set of possible true states under unknown bath–environment interactions
List To Do Tasks Checklist Streamline Icon: https://streamlinehq.com

Collections

Sign up for free to add this paper to one or more collections.

User Circle Single Streamline Icon: https://streamlinehq.com Sign Up
X Twitter Logo Streamline Icon: https://streamlinehq.com

Tweets

This paper has been mentioned in 2 tweets and received 213 likes.

Upgrade to Pro to view all of the tweets about this paper:

Start a free 7-day Pro trial