MathCanvas: Intrinsic Visual Chain-of-Thought for Multimodal Mathematical Reasoning (2510.14958v1)

Abstract: While LLMs have excelled in textual reasoning, they struggle with mathematical domains like geometry that intrinsically rely on visual aids. Existing approaches to Visual Chain-of-Thought (VCoT) are often limited by rigid external tools or fail to generate the high-fidelity, strategically-timed diagrams necessary for complex problem-solving. To bridge this gap, we introduce MathCanvas, a comprehensive framework designed to endow unified Large Multimodal Models (LMMs) with intrinsic VCoT capabilities for mathematics. Our approach consists of two phases. First, a Visual Manipulation stage pre-trains the model on a novel 15.2M-pair corpus, comprising 10M caption-to-diagram pairs (MathCanvas-Imagen) and 5.2M step-by-step editing trajectories (MathCanvas-Edit), to master diagram generation and editing. Second, a Strategic Visual-Aided Reasoning stage fine-tunes the model on MathCanvas-Instruct, a new 219K-example dataset of interleaved visual-textual reasoning paths, teaching it when and how to leverage visual aids. To facilitate rigorous evaluation, we introduce MathCanvas-Bench, a challenging benchmark with 3K problems that require models to produce interleaved visual-textual solutions. Our model, BAGEL-Canvas, trained under this framework, achieves an 86% relative improvement over strong LMM baselines on MathCanvas-Bench, demonstrating excellent generalization to other public math benchmarks. Our work provides a complete toolkit-framework, datasets, and benchmark-to unlock complex, human-like visual-aided reasoning in LMMs. Project Page: https://mathcanvas.github.io/

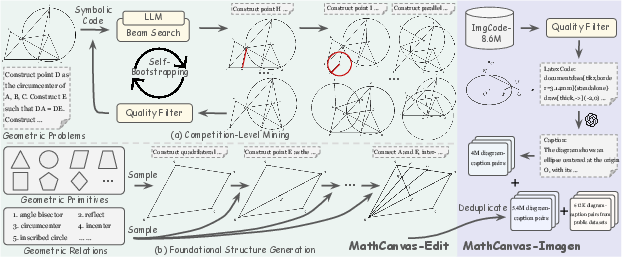
• The paper introduces MathCanvas, a framework that integrates diagram editing with textual chain-of-thought reasoning for multimodal mathematical problem solving.
• It leverages three large, curated datasets to train models on iterative diagram generation and visual manipulation using a two-stage training recipe.
• Experimental results on MathCanvas-Bench show significant gains in geometry tasks, with BAGEL-Canvas outperforming prior models in weighted scoring metrics.

MathCanvas: Intrinsic Visual Chain-of-Thought for Multimodal Mathematical Reasoning

Motivation and Problem Statement

Mathematical reasoning, especially in geometry and function analysis, fundamentally relies on the construction and manipulation of visual aids. While LLMs have achieved strong performance in textual chain-of-thought (CoT) reasoning, their capabilities are limited in domains where visual intuition is essential. Prior approaches to Visual Chain-of-Thought (VCoT) either depend on rigid external tools or fail to generate high-fidelity, strategically-timed diagrams, resulting in suboptimal or incorrect solutions. The MathCanvas framework addresses these deficiencies by enabling unified Large Multimodal Models (LMMs) to natively interleave visual synthesis and editing with textual reasoning, thereby unlocking intrinsic VCoT for complex mathematical problem solving.

Dataset Construction and Curation Pipeline

MathCanvas introduces three major datasets:

• MathCanvas-Edit: 5.2M step-by-step diagram editing trajectories, constructed via a hybrid pipeline combining competition-level geometry mining (using AlphaGeometry LLM with beam search) and systematic generation of foundational geometric structures. This dataset imparts iterative diagram editing skills, covering both complex and fundamental geometric operations.
• MathCanvas-Imagen: 10M caption-to-diagram pairs, aggregated from MathCanvas-Edit, code-derived captions (using ImgCode-8.6M and GPT-4.1-mini for natural language generation), and public resources (MAVIS, TR-CoT). This corpus teaches models to synthesize diagrams from textual descriptions.
• MathCanvas-Instruct: 219K interleaved visual-textual reasoning examples, curated from 632K multimodal math problems via multi-stage filtering (GPT-5 for relevance and error removal, SwinIR for image enhancement, deduplication for diversity). Each example contains a sequence of textual and visual steps, enabling strategic reasoning.

  Figure 1: The curation pipeline for the MathCanvas-Edit and MathCanvas-Imagen dataset.

Benchmarking and Statistical Analysis

MathCanvas-Bench is a dedicated benchmark comprising 3K problems sampled from MathCanvas-Instruct, designed to rigorously evaluate interleaved image-textual reasoning. Problems are balanced across mathematical domains and filtered to prevent data leakage. The evaluation protocol uses GPT-4.1 for automated answer extraction and correctness judgment, employing both complete accuracy and a weighted scoring metric that values later sub-questions more heavily.

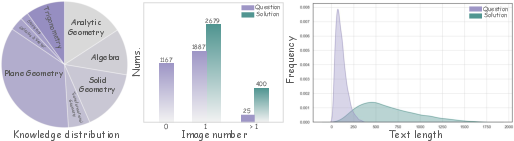
Figure 2: Statistical analysis of the MathCanvas-Bench test set, including knowledge type distribution, image count per question/solution, and text length distributions.

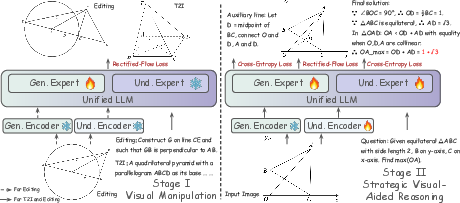
Two-Stage Training Recipe

The MathCanvas framework is instantiated on the BAGEL unified LMM architecture, which features separate transformer experts for understanding and generation. The training paradigm consists of two stages:

• Stage I: Visual Manipulation The Generation Expert is pretrained on MathCanvas-Edit and MathCanvas-Imagen, learning both diagram generation and iterative editing. The understanding pathway is frozen, and training is performed using a Rectified-Flow Loss for robust visual synthesis.
• Stage II: Strategic Visual-Aided Reasoning The entire model is fine-tuned on MathCanvas-Instruct, learning to interleave visual actions with textual reasoning. The model predicts when to draw (<|vision_start|>) or conclude (<|endoftext|>), and images in solutions are generated via noised VAE tokens with Rectified-Flow Loss. All components are unfrozen for joint optimization, and dual Classifier-Free Guidance is used during inference.

  Figure 3: The two-stage training recipe for MathCanvas, showing pretraining on visual manipulation and fine-tuning for strategic visual-aided reasoning.

Dataset and Example Diversity

MathCanvas-Instruct covers a broad taxonomy of mathematical knowledge points, with 65% multimodal and 35% text-only questions, spanning middle and high school curricula. The average solution length is 540 tokens, and solutions may contain up to five images, supporting complex, multi-step reasoning.

Figure 4: Distribution of knowledge type of MathCanvas-Instruct dataset.

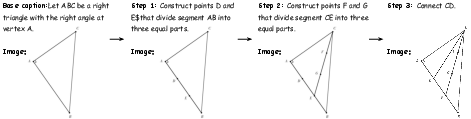
Figure 5: An example from MathCanvas-Edit dataset, illustrating step-by-step diagram editing.

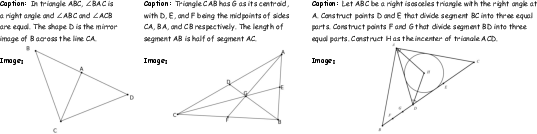
Figure 6: Examples from MathCanvas-Imagen dataset, demonstrating caption-to-diagram generation.

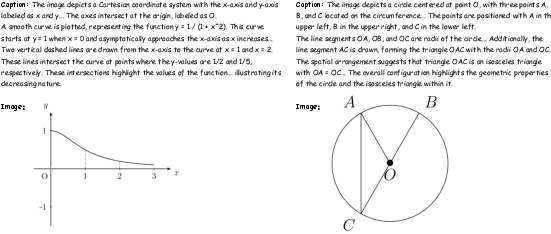
Figure 7: Additional examples from MathCanvas-Imagen dataset.

Figure 8: An example from MathCanvas-Instruct dataset, showing interleaved visual-textual reasoning.

Figure 9: Another example from MathCanvas-Instruct dataset.

Figure 10: Further example from MathCanvas-Instruct dataset.

Qualitative Comparison with Prior Methods

MathCanvas demonstrates clear advantages over previous intrinsic VCoT models (e.g., BAGEL-Zebra-CoT, Nano-Banana), which either generate geometrically invalid diagrams or fail to strategically employ visuals. In contrast, MathCanvas produces correct intermediate visual steps that unlock elegant solution paths.

Figure 11: Leading LMMs (Gemini-2.5-Pro and GPT-5) solving a problem via text-only reasoning, highlighting the limitations of non-visual approaches.

Figure 12: Comparison of BAGEL-Zebra-CoT, Nano-Banana, and MathCanvas, illustrating superior strategic visual reasoning.

Experimental Results and Ablations

On MathCanvas-Bench, BAGEL-Canvas achieves a weighted score of 34.4%, outperforming all open-source models and several proprietary systems. The model exhibits the largest gains in geometry-heavy subjects (Trigonometry +27.1, Plane Geometry +19.2, Solid Geometry +12.3), validating the hypothesis that visual reasoning is critical for these domains. Ablation studies confirm that both diagram editing and generation pretraining are essential, and that interleaved visual-textual training fundamentally enhances textual reasoning even in text-only benchmarks.

Implementation Details

Training is performed on 16 NVIDIA H800 GPUs using AdamW optimizer. Stage I uses a learning rate of $2 \times 10^{-5}$ for 80K steps, with the understanding expert frozen. Stage II uses $1 \times 10^{-5}$ for 16K steps, with all components unfrozen. Losses include Rectified-Flow for images and cross-entropy for token prediction. Dropout rates are tuned for regularization, and batch sizes are set to maximize GPU utilization.

Implications and Future Directions

MathCanvas establishes a new paradigm for multimodal mathematical reasoning, demonstrating that intrinsic VCoT can be effectively realized in unified LMMs. The framework, datasets, and benchmark provide a robust foundation for future research in dynamic, process-oriented multimodal reasoning. Potential extensions include scaling to higher-dimensional mathematics, integrating symbolic computation, and exploring agentic capabilities for interactive problem solving.

Conclusion

MathCanvas presents a comprehensive solution to the challenge of intrinsic visual chain-of-thought reasoning in mathematics. By combining large-scale visual manipulation and strategic reasoning datasets with a two-stage training recipe, the framework enables LMMs to autonomously generate and edit diagrams as part of their reasoning process. The resulting model, BAGEL-Canvas, achieves substantial improvements over prior baselines, particularly in geometry and other visually intensive domains. This work sets a new standard for multimodal mathematical reasoning and opens avenues for further advancements in AI-driven problem solving.